1. 引言
多匝空心线圈是实现电场和磁场相互转换的重要工具之一。感应电压与空间磁场的关系可依据电磁感应原理确定,基于空心线圈的磁场传感器广泛地应用在多种测量领域,如Rogowski线圈、电容电压互感器(CVT)和瞬变电磁传感器。由于电感和分布电容的存在,线圈输出电压不能准确跟随突变的感应电压,使得接收到的早期信号发生畸变,这种现象称为线圈的过渡过程。文献 [1] [2] 提出随着匝数增加,线圈固有过渡过程影响,加剧影响了瞬变电磁法的浅层探测效果。
接收线圈频带宽度对输出信号的影响如图1所示,蓝色实线表示一次场消失后接收线圈的感应电动势
,10 kHz带宽的接收线圈输出信号
如红色虚线所示,而50 kHz带宽的接收线圈输出信号
如黄色点线所示。
由图1可知在过渡过程影响下,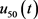 在
时开始衰减,峰值为4.2 V,而
在
时开始衰减,其峰值仅为2.95 V。接收线圈频带宽度的下降加剧了输出信号的过渡过程,降低了线圈对感应电动势的跟随能力,这种畸变降低了探测结果的可靠性 [3] [4]。因此,针对过渡过程的线圈优化与线圈标定是该领域的研究热点。
在
时开始衰减,峰值为4.2 V,而
在
时开始衰减,其峰值仅为2.95 V。接收线圈频带宽度的下降加剧了输出信号的过渡过程,降低了线圈对感应电动势的跟随能力,这种畸变降低了探测结果的可靠性 [3] [4]。因此,针对过渡过程的线圈优化与线圈标定是该领域的研究热点。
文献 [5] 为不同有效接收面积的接收线圈设计了最佳半径,降低了过渡过程对浅层探测的影响。文献 [6] 以提高带宽为目标设计了矿井瞬变电磁探测传感器,具有小电感弱分布电容的接收线圈在匹配临界阻尼的情况下实现了较好的信号跟踪效果。文献 [7] 认为接收线圈的弱欠阻尼状态最有利于减小过渡过程对信号的影响。
感应电压与输出电压的关系可以由线圈的传递函数唯一确定,文献 [8] 通过拟合Rogowski线圈的频率响应,获得线圈的传递函数,实现过渡过程的消除;文献 [9] 在屏蔽室内使用螺线管产生标定磁场,通过测量混场源电磁传感器的频率响应,实现传感器的标定;文献 [8] [10] 采用谐振法对线圈施加扫频信号获得其谐振频率,通过计算分别获得了Tesla变换器和Rogowski线圈的参数。但是,频率响应和谐振点的测量需要高精度的信号发生器和高频示波器,这种标定方法只能在实验室完成,不利于现场作业。

Figure 1. The effect of the transition process of the receiving coil on the signal
图1. 接收线圈的过渡过程对信号的影响
文献 [11] [12] [13] 提出基于导电环的地面瞬变电磁标定系统,实现了过渡过程的定量分析,然而由于各种非期望响应的存在,很难通过一定的函数关系把测量值还原为真实的感应电压,同时也对高电导率土壤的适应性较差。
文献 [5] 指出,在隧道探测与矿产勘探应用领域,空心线圈装置的电感参数受环境介质的相对磁导率影响明显。文献 [14] 指出用于测量电力工业中的Rogowski线圈,当环境温度变化时,热膨胀可以改变线圈的横截面积,改变了线圈的参数。这种由测试环境引起的参数变化很难在实验室中模拟,需要寻找一种在线的标定方案。
本文研究了瞬变电磁空心线圈传感器等效电路模型,提出了利用传递函数消除过渡过程的方案,以及适用于现场环境下求解接收线圈参数的变阻尼标定法。
2. 空心线圈的过渡过程
瞬变电磁空心接收线圈分布参数等效电路如图2所示。
其中,
为接收线圈的感应电动势,L为接收线圈的等效电感,R为接收线圈的内阻,C为接收线圈的分布电容,
为并联在接收线圈两端的阻尼电阻,
为线圈的实际输出信号。消除线圈过渡过程就是通过
还原感应电动势
。
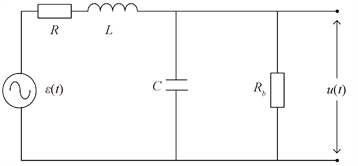
Figure 2. Equivalent circuit of receiving coil distributed parameter
图2. 接收线圈分布参数等效电路
设L和C无初始储能,
和测量电压
的关系可由图2推导得:
(1)
式(1)经过拉普拉斯逆变换可简化为:
(2)
其中
,
为线圈谐振频率。
定义阻尼系数,
(3)
在欠阻尼状态下
,阶跃响应将呈现振荡,波形严重畸变,过阻尼状态下
,响应衰减缓慢,其过渡过程较长。在临界阻尼
的条件下,可解得临界阻尼电阻为:
(4)
虽然线圈处于临界阻尼状态时可以缓解过度过程 [15],但仍然无法将其消除。文献 [5] 指出,根据
的视电阻率计算存在较大误差。
如果线圈的等效电路参数已知,便可以根据(1)式传递函数通过测量电压获得感应电压数据。
3. 变阻尼标定法
本文提出一种新的解决方案:变阻尼标定法。
变阻尼标定法基于以下三点假设:
假设①:电路的分布参数模型符合图2所述结构;
假设②:阻尼电阻
和线圈的内阻R已知;
假设③:在测量不同
的线圈响应信号时,原始的激励不变,即
保持不变。
为避免将测量电压
可能含有的高频噪声放大,改写(2)式微分方程为积分方程式:
(5)
其中
,
,
,线圈的内阻r可通过测量获取,由假设②,将
按预设值的1、0.9、
0.8倍关系选取三个阻尼电阻值,获得三个参数方程。
在相同的激励源作用下,由三个不同阻尼参数的线圈得到三组响应信号
、
、
,将其分别代入到式(5)中得:
(6)
式中未知量
,
和
分别为不同阻尼电阻下的
与
值以及
,而
、
和
可以通过A/D采样直接得到。求解方程组(6)便可以确定参数
和
,进而获取线圈的传递函数
。
由于式(6)是三元二次方程组,因此可能存在两组不同的实数解,但其中仅有一组正解。可以通过式(4)分别求解两组解对应的临界阻尼电阻值,将过小的正值或负值的解舍弃即可。
为验证待定参数方程的正确性,在MATLAB中建立仿真模型。按假设①,假设②设置的三组接收线圈的参数值,在Simulink模块中建立仿真模型,当发射电流关断时间为15 µs时,得到三组畸变的响应信号
、
、
,如图3所示,在工程中可由测量获得。将这三组数据代入方程式(6)中,求解出线圈的结构参数
与
并和初设的参数值L,C相比较即可获得误差率
。
(7)
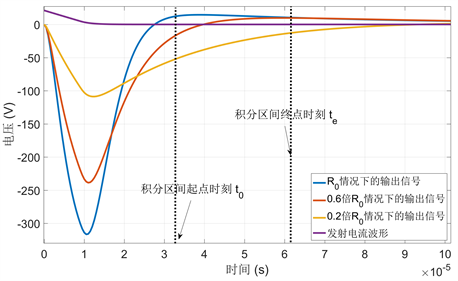
Figure 3. The measured voltage curve of the variable damping calibration method
图3. 变阻尼标定法的测量电压曲线
4. 讨论
4.1. 采样率对结果的影响
较低的采样率会降低测量电压曲线的准确性,尤其会影响图1所示峰值的完整性,从而降低方程组(6)积分变量的精度,扩大待求参数的误差。
如表1所示,预设的参数值
,
,参数求解的误差率随采样率的降低而增加,当发射电流关断时间为15 µs时,采样率应不低于5 MHz,以获得较好的参数求解精度。
4.2. 阻尼电阻Rb对结果的影响
将
按临界值的不同倍数关系选取三个阻尼电阻值,在相同的激励源作用下,得到三组响应信号
、
、
组成方程组,考察阻尼电阻的选取对参数求解精度的影响。

Table 1. The influence of sampling rate on parameter solution error rate
表1. 采样率对参数求解误差率的影响
固定采样率为5 MHz,从临界阻尼值
开始,将三个阻尼电阻值设置为递减的等差数列,观察求得的参数误差率随公差的变化情况如表2所示。

Table 2. The relationship between parameter error rate and tolerance of damping resistance
表2. 参数误差率与阻尼电阻数列公差的关系
由表2可知,参数误差率随公差的增大而减小,这主要是因为较大的公差增加了不同测量电压曲线在同一时刻的差异程度,提高了方程组(6)的求解精度。因此,可以将
按临界值的1、0.6、0.2倍选取阻尼电阻值。
4.3. 积分区间对结果的影响
由于较低的采样率会影响峰值的完整性,因此,除了使用高采样率的采集器,提高求解精度的另一种有效手段是合理选择积分区间,避开对采样率要求较高的测量电压曲线峰值部分。
以图3所示的测量电压曲线为例,固定采样率为5 MHz,分别选择2 µs,30 µs和50 µs作为积分起始点,观察积分200 µs后参数求解情况如表3所示。

Table 3. The influence of the integration starting point on the error rate of parameter solution
表3. 积分起始点对参数求解误差率的影响
由表3可知,若积分区间包含测量电压峰值,误差率受采样率的影响明显;若积分起始时刻为30 µs,积分区间位于测量电压峰值之后,误差率降为1.22‰;当积分起始时刻为50 µs,虽然积分区间位于测量电压峰值之后,但是误差率升高到2.81‰,这主要是由于
情况下三个测量电压曲线的差异程度较低所致。
因此,通过选择适当的积分起始点
,使得
位于测量电压峰值之后,且使得三条测量电压曲线在
时刻的幅值有较大的差异,可以获得较高的求解精度。
5. 实验结果
为了检验本文提出标定方案的效果,在重庆大学校内防空洞上方实施了一个对比实验。实验采用重庆大学研制的FCTEM瞬变电磁设备,沿着防空洞布置74个测点,如图4(a)所示。发射电流23 A,关断时间21 µs,使用变阻尼标定算法在线矫正线圈的过渡过程,矫正前后的视电阻率成像结果分别如图4(b)、图4(c)所示:
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 4. Comparison of apparent resistivity imaging results before and after the transition process, (a) the schematic diagram of the air-raid shelter distribution; (b) before the transition process; (c) after the transition process
图4. 过渡过程处理前后的视电阻率成像结果对比,(a) 防空洞分布示意图;(b) 过渡过程处理前;(c) 过渡过程处理后
由图4可知,经过矫正后的数据可以更准确的反映出防空洞在地下的分布情况,可以清晰的辨识到防空洞顶部距地表的分界面以及位于第15号测点与第60号测点的洞壁。显著提高了瞬变电磁法浅层探测效果。
6. 小结
本文根据感应式空心线圈传感器的等效电路模型,建立了空心线圈的传递函数,提出了利用传递函数消除过渡过程的方案,通过分析线圈阻尼电阻与输出波形的关系,提出了采用变阻尼积分方程获取线圈等效参数的方法。该方法可应用于瞬变电磁接收线圈的现场标定,有利于提高传感器的探测效果。