具反馈控制和Beddington-DeAngelis功能反应的离散竞争系统的持久性

doi:10.12677/AAM.2020.910193

期刊菜单

具反馈控制和Beddington-DeAngelis功能反应的离散竞争系统的持久性
Permanence of a Discrete Competitive System with Feedback Controls and Beddington-DeAngelis Functional Response

DOI: 10.12677/AAM.2020.910193, PDF, HTML, XML, 下载: 608 浏览: 780 科研立项经费支持
作者: 余胜斌：阳光学院基础教研部，福建福州
关键词: 反馈控制；Beddington-DeAngelis；持久性；离散；竞争；Feedback Controls； Beddington-DeAngelis； Permanence； Discrete； Competitive

摘要: 借助差分不等式，研究一类具Beddington-DeAngelis功能反应和反馈控制的离散非自治竞争系统的持久性，得到了一组新的持久性条件，从而改进了已有的工作。数值模拟验证了结果的可靠性。

Abstract: We consider a discrete nonautonomous competitive system with Beddington-DeAngelis functional response and feedback controls. Using difference inequality theory, new conditions on permanence of the system are obtained. The results improve the recent one obtained by Zhang Jiehua. The numerical simulations show the feasibility of our results.

文章引用：余胜斌. 具反馈控制和Beddington-DeAngelis功能反应的离散竞争系统的持久性[J]. 应用数学进展, 2020, 9(10): 1665-1671. https://doi.org/10.12677/AAM.2020.910193

1. 引言

对有界的非负序列 ${h (n)}$ ，定义：

$h^{L} = \inf_{n \in N} {h (n)}, h^{U} = \sup_{n \in N} {h (n)} .$

近年来，学者们较多地关注生态系统中种群间重要关系–竞争 [1] - [8]，得到了丰富的研究成果。张杰华 [1] 研讨了下列具Beddington-DeAngelis功能反应和反馈控制的竞争系统：

${\begin{cases} x_{1} (n + 1) = x_{1} (n) \exp {r_{1} (n) - a_{1} (n) x_{1} (n) - \frac{b_{1} (n) x_{2} (n)}{α_{1} (n) + β_{1} (n) x_{1} (n) + γ_{1} (n) x_{2} (n)} - c_{1} (n) u_{1} (n)}, \\ x_{2} (n + 1) = x_{2} (n) \exp {r_{2} (n) - a_{2} (n) x_{2} (n) - \frac{b_{2} (n) x_{1} (n)}{α_{2} (n) + β_{2} (n) x_{1} (n) + γ_{2} (n) x_{2} (n)} - c_{2} (n) u_{2} (n)}, \\ Δ u_{1} (n) = - e_{1} (n) u_{1} (n) + d_{1} (n) x_{1} (n), \\ Δ u_{2} (n) = - e_{2} (n) u_{2} (n) + d_{2} (n) x_{2} (n), \end{cases}$ (1)

其中 $x_{i} (n)$ 和 $u_{i} (n)$ 为第n代种群i的密度及其对应的反馈控制；非负序列 $r_{i} (n)$ ， $a_{i} (n)$ ， $b_{i} (n)$ ， $c_{i} (n)$ ， $d_{i} (n)$ ， $e_{i} (n)$ ， $α_{i} (n)$ ， $β_{i} (n)$ ， $γ_{i} (n)$ 的上下界为正且 $0 < e_{i}^{L} \leq e_{i} (n) \leq e_{i}^{M} < 1 (i = 1, 2)$ 。在无反馈控制变量影响的情况下，陈凤德等学者在文 [2] [3] 中最早提出了系统(1)所对应的连续系统，并探讨了该系统在有和无毒素影响的下的绝灭性、持久性、稳定性及概周期解的存在性等问题。考虑到离散系统对种群世代不重叠或数量很少时的更精准描述，张杰华在文 [2] [3] 的基础上探讨了系统(1)在无反馈控制变量影响下的绝灭性和稳定性问题。之后，张杰华 [1] 进一步考虑了反馈控制对系统的影响，在假定系统(1)满足初始条件：

$x_{i} (0) > 0, u_{i} (0) > 0,$ (2)

及各系数均为概周期函数的条件下，运用差分不等式、Lyapunov函数法和概周期的相关理论，得到了系统(1)的唯一全局吸引的正概周期解和下列的持久性论述：

定理A定义 $M_{i} = \frac{\exp (r_{i}^{U} - 1)}{a_{i}^{L}}$ ， $W_{i} = \frac{M_{i} d_{i}^{U}}{e_{i}^{L}}$ ，若

(H₀) $r_{i}^{L} α_{i}^{L} > (b_{i}^{U} - r_{i}^{L} γ_{i}^{L}) M_{j} + c_{i}^{U} W_{i} (α_{i}^{L} + γ_{i}^{L} M_{j}), (i, j = 1, 2 且 i \neq j),$

成立，则存在正常数 $m_{i}, w_{i}$ 和 $M_{i}, W_{i} (i = 1, 2)$ ，使得对系统(1)的任意正解 ${(x_{1} (n), x_{2} (n), u_{1} (n), u_{2} (n))}^{T}$ 均满足：

$m_{i} \leq \lim_{n \to + \infty} \inf x_{i} (n) \leq \underset{n \to + \infty}{\lim \sup} x_{i} (n) \leq M_{i}, w_{i} \leq \lim_{n \to + \infty} \inf u_{i} (n) \leq \underset{n \to + \infty}{\lim \sup} u_{i} (n) \leq W_{i}, i = 1, 2.$

由(H₀)易知，反馈控制变量会影响该系统的持久性，但近期的研究结果表明，持久性与反馈控制无关 [8] [9] [10] [11] [12]。于是，我们迫切需要知道：反馈控制对系统(1)的持久性是否也不起任何作用呢？借助文 [8] [9] [10] [11] [12] 的研究方法，我们有：

定理B若(H) $r_{i}^{L} α_{i}^{L} > (b_{i}^{U} - r_{i}^{L} γ_{i}^{L}) M_{j}, (i, j = 1, 2 且 i \neq j)$ 成立，则系统(1)永久持续生存。

注1：注意到(H₀)比(H)强，且(H)与反馈控制无关，说明反馈控制不会对系统(1)的持久性产生影响,故定理B极大地改进了张杰华 [1] 的结论。

2. 引理及结论证明

引理1 [13]。设 $a (n), b (n)$ 为非负序列且其上下界为正，进一步假设正序列 ${x (n)}$ 满足 $x (n + 1) \geq x (n) \exp {a (n) - b (n) x (n)}$ ， $n \geq N_{0}$ ， $N_{0} \in N$ 和 $\underset{n \to + \infty}{\lim \sup} x (n) \leq x^{*}$ ，则

$\underset{n \to + \infty}{\lim \inf} x (n) \geq \min {\frac{a^{L}}{b^{U}} \exp {a^{L} - b^{U} x^{*}}, \frac{a^{L}}{b^{U}}} .$

引理2 [12]。若 $A > 0, y (0) > 0$ 且 $y (n + 1) \leq A y (n) + B (n), n = 1, 2, \dots$ ，则

$y (n) \leq A^{k} y (n - k) + \sum_{i = 0}^{k - 1} A^{i} B (n - i - 1), k \leq n .$

进一步地，若 $A < 1$ 且B有上界M，则 $\underset{n \to + \infty}{\lim \inf} y (n) \geq \frac{M}{1 - A}$ 。

引理3 [12]。若 $A > 0, y (0) > 0$ 且 $y (n + 1) \geq A y (n) + B (n), n = 1, 2, \dots$ ，则有

$y (n) \geq A^{k} y (n - k) + \sum_{i = 0}^{k - 1} A^{i} B (n - i - 1), k \leq n .$

进一步地，若 $A < 1$ 且B有下界m，则 $\underset{n \to + \infty}{\lim \inf} y (n) \geq \frac{m}{1 - A}$ 。

引理4 [1]。系统(1)的任一正解 ${(x_{1} (n), x_{2} (n), u_{1} (n), u_{2} (n))}^{T}$ 满足：

$\underset{n \to + \infty}{\lim \sup} x_{i} (n) \leq \frac{\exp (r_{i}^{U} - 1)}{a_{i}^{L}} ≜ M_{i}, \underset{n \to + \infty}{\lim \sup} u_{i} (n) \leq \frac{M_{i} d_{i}^{U}}{e_{i}^{L}} ≜ W_{i}, i = 1, 2.$

引理5。若(H₁) $r_{1}^{L} α_{1}^{L} > (b_{1}^{U} - r_{1}^{L} γ_{1}^{L}) M_{2}$ 成立，则对系统(1)的任一正解 ${(x_{1} (n), x_{2} (n), u_{1} (n), u_{2} (n))}^{T}$ ，有 $\underset{n \to + \infty}{\lim \inf} x_{1} (n) \geq m_{1}$ ， $\underset{n \to + \infty}{\lim \inf} u_{1} (n) \geq w_{1}$ ，这里 $m_{1}, w_{1} > 0$ 为常数。

证明根据引理4，对 $\forall ε > 0$ ， $\exists N_{1} > 0$ ，当 $n \geq N_{1}$ 时，有

$x_{i} (n) \leq M_{i} + ε ≜ M_{i ε}, u_{i} (n) \leq W_{i} + ε ≜ W_{i ε}, i = 1, 2.$

结合(H₁)，对上面的 $ε > 0$ ，存在足够小的 $ξ_{1} > 0$ ，满足

$r_{1}^{L} α_{1}^{L} - (b_{1}^{U} - r_{1}^{L} γ_{1}^{L}) M_{2 ε} > ξ_{1} .$ (3)

由系统(1)的第一个方程及(3)式可得，若 $n \geq N_{1}$ ，则有

$\begin{matrix} x_{1} (n + 1) \geq x_{1} (n) \exp {r_{1}^{L} - a_{1}^{U} M_{1 ε} - \frac{b_{1}^{U} M_{2 ε}}{α_{1}^{L}} - c_{1}^{U} W_{1 ε}} \\ \geq x_{1} (n) \exp {- a_{1}^{U} M_{1 ε} - \frac{b_{1}^{U} M_{2 ε}}{α_{1}^{L}} - c_{1}^{U} W_{1 ε}} ≜ x_{1} (n) \exp {Q_{1 ε}}, \end{matrix}$ (4)

其中 $Q_{1 ε} = - a_{1}^{U} M_{1 ε} - \frac{b_{1}^{U} M_{2 ε}}{α_{1}^{L}} - c_{1}^{U} W_{1 ε} < 0$ 。对 $\forall k \leq n$ 来说，根据(4)式可得，

$\prod_{j = n - k}^{n - 1} \frac{x_{1} (j + 1)}{x_{1} (j)} \geq \prod_{j = n - k}^{n - 1} \exp {Q_{1 ε}} = \exp {k Q_{1 ε}}$ 即 $x_{1} (n - k) \leq x_{1} (n) \exp {- k Q_{1 ε}} .$ (5)

根据系统(1)可知

$u_{1} (n + 1) \leq (1 - e_{1}^{L}) u_{1} (n) + d_{1}^{U} x_{1} (n) ≜ A_{1} u_{1} (n) + B_{1} (n),$ (6)

这里 $A_{1} = 1 - e_{1}^{L}, B_{1} (n) = d_{1}^{U} x_{1} (n)$ 。对 $\forall k \leq n$ ，结合(5)-(6)式和引理2可得，

$\begin{matrix} u_{1} (n) \leq A_{1}^{k} u_{1} (n - k) + \sum_{i = 0}^{k - 1} A_{1}^{i} B_{1} (n - i - 1) \\ = A_{1}^{k} u_{1} (n - k) + \sum_{i = 0}^{k - 1} A_{1}^{i} d_{1}^{U} x_{1} (n - i - 1) \\ \leq A_{1}^{k} u_{1} (n - k) + d_{1}^{U} x_{1} (n) \sum_{i = 0}^{k - 1} A_{1}^{i} \exp {- (i + 1) Q_{1 ε}} . \end{matrix}$ (7)

根据 $0 < e_{1}^{L} < 1$ 可知 $0 < A_{1} < 1$ ，故当 $k \to + \infty$ 时，有 $0 \leq A_{1}^{k} W_{1 ε} \to 0$ 。 (8)

固定 $N_{2} = \max {N_{1}, \frac{\ln E_{1}}{\ln A_{1}}} + 1$ ，这里 $E_{1} = \frac{ξ_{1}}{2 c_{1}^{U} (α_{1}^{L} + γ_{1}^{L} M_{2 ε}) W_{1 ε}}$ ，从而当 $n \geq N_{2}$ 时，有

$c_{1}^{U} A_{1}^{N_{2}} W_{1 ε} < \frac{ξ_{1}}{2 (α_{1}^{L} + γ_{1}^{L} M_{2 ε})} .$ (9)

另一方面，当 $n \geq N_{1} + N_{2}$ 时，我们可得

$\begin{matrix} u_{1} (n) \leq A_{1}^{N_{2}} u_{1} (n - N_{2}) + d_{1}^{U} x_{1} (n) \sum_{i = 0}^{N_{2} - 1} A_{1}^{i} \exp {- (i + 1) Q_{1 ε}} \\ \leq A_{1}^{N_{2}} W_{1 ε} + d_{1}^{U} x_{1} (n) \sum_{i = 0}^{N_{2} - 1} A_{1}^{i} \exp {- (i + 1) Q_{1 ε}} ≜ A_{1}^{N_{2}} W_{1 ε} + D_{1 ε} x_{1} (n), \end{matrix}$ (10)

其中 $D_{1 ε} = d_{1}^{U} \sum_{i = 0}^{N_{2} - 1} A_{1}^{i} \exp {- (i + 1) Q_{1 ε}}$ 。

结合系统(1)、(3)式和(9)-(10)式可知，

$\begin{matrix} x_{1} (n + 1) \geq x_{1} (n) \exp {r_{1}^{L} - a_{1}^{U} x_{1} (n) - \frac{b_{1}^{U} M_{2 ε}}{α_{1}^{L} + γ_{1}^{L} M_{2 ε}} - c_{1}^{U} u_{1} (n)} \\ \geq x_{1} (n) \exp {r_{1}^{L} - a_{1}^{U} x_{1} (n) - \frac{b_{1}^{U} M_{2 ε}}{α_{1}^{L} + γ_{1}^{L} M_{2 ε}} - c_{1}^{U} [A_{1}^{N_{2}} W_{1 ε} + D_{1 ε} x_{1} (n)]} \\ \geq x_{1} (n) \exp {r_{1}^{L} - (a_{1}^{U} + c_{1}^{U} D_{1 ε}) x_{1} (n) - \frac{b_{1}^{U} M_{2 ε}}{α_{1}^{L} + γ_{1}^{L} M_{2 ε}} - c_{1}^{U} A_{1}^{N_{2}} W_{1 ε}} \\ \geq x_{1} (n) \exp {\frac{ξ_{1}}{2 (α_{1}^{L} + γ_{1}^{L} M_{2 ε})} - (a_{1}^{U} + c_{1}^{U} D_{1 ε}) x_{1} (n)} ≜ x_{1} (n) \exp {F_{1} - F_{2 ε} x_{1} (n)}, \end{matrix}$ (11)

其中 $F_{1} = \frac{ξ_{1}}{2 (α_{1}^{L} + γ_{1}^{L} M_{2 ε})}$ ， $F_{2 ε} = a_{1}^{U} + c_{1}^{U} D_{1 ε}$ 。借助引理1和上式可得，

$\underset{n \to + \infty}{\lim \inf} x_{1} (n) \geq \min {\frac{F_{1}}{F_{2 ε}} \exp {F_{1} - F_{2 ε} M_{1}}, \frac{F_{1}}{F_{2 ε}}} .$

取 $ε \to 0$ ，则有 $\underset{n \to + \infty}{\lim \inf} x_{1} (n) \geq \min {\frac{F_{1}}{F_{2}} \exp {F_{1} - F_{2} M_{1}}, \frac{F_{1}}{F_{2}}} ≜ m_{1}$ 。

故 $\exists N_{3} \geq N_{1} + N_{2}$ ，当 $n \geq N_{3}$ 时，我们有 $x_{1} (n) \geq \frac{m_{1}}{2}$ 。

由此及系统(1)易得， $Δ u_{1} (n) \geq - e_{1} (n) u_{1} (n) + \frac{m_{1} d_{1} (n)}{2}, \forall n \geq N_{3}$ 。

即有 $u_{1} (n + 1) \geq (1 - e_{1}^{U}) u_{1} (n) + \frac{m_{1} d_{1}^{L}}{2}$ 。再根据引理3可知， $\underset{n \to + \infty}{\lim \inf} u_{1} (n) \geq \frac{m_{1} d_{1}^{L}}{2 e_{1}^{U}} ≜ w_{1}$ 。证毕。

类似地，我们有：

引理6 若(H₂) $r_{2}^{L} α_{2}^{L} > (b_{2}^{U} - r_{2}^{L} γ_{2}^{L}) M_{1}$ 成立，则对系统(1)的任一正解 ${(x_{1} (n), x_{2} (n), u_{1} (n), u_{2} (n))}^{T}$ ，有 $\underset{n \to + \infty}{\lim \inf} x_{2} (n) \geq m_{2}$ ， $\underset{n \to + \infty}{\lim \inf} u_{2} (n) \geq w_{2}$ ，这里 $m_{2}, w_{2} > 0$ 为常数。

结合引理5和6可推得定理B成立。

3. 数值模拟

例1 考虑系统

${\begin{cases} x_{1} (n + 1) = x_{1} (n) \exp {1.8 + 0.2 \cos (\sqrt{3} n) - x_{1} (n) - \frac{(0.06 + 0.04 \cos (\sqrt{11} n)) x_{2} (n)}{0.6 + 2 x_{1} (n) + x_{2} (n)} - 2 u_{1} (n)}, \\ x_{2} (n + 1) = x_{2} (n) \exp {2.9 + 0.1 \sin (\sqrt{13} n) - x_{2} (n) - \frac{(0.07 + 0.03 \cos (\sqrt{5} n)) x_{1} (n)}{0.8 + 2 x_{1} (n) + x_{2} (n)} - 3 u_{2} (n)}, \\ Δ u_{1} (n) = - (0.45 + 0.3 \cos (\sqrt{5} n)) u_{1} (n) + (0.5 + 0.3 \sin (\sqrt{7} n)) x_{1} (n), \\ Δ u_{2} (n) = - (0.5 + 0.1 \sin (\sqrt{7} n)) u_{2} (n) + (0.05 + 0.02 \cos (\sqrt{3} n)) x_{2} (n), \end{cases}$ (12)

借助引理4和文 [1] 的定理2.1，我们可得

$M_{1} = \frac{\exp (r_{1}^{U} - 1)}{a_{1}^{L}} \approx 2 .7183, M_{2} = \frac{\exp (r_{2}^{U} - 1)}{a_{2}^{L}} \approx 7 .3891, W_{1} = \frac{M_{1} d_{1}^{U}}{e_{1}^{L}} \approx 3 .6244 .$

故 $r_{1}^{L} α_{1}^{L} - (b_{1}^{U} - r_{1}^{L} γ_{1}^{L}) M_{2} \approx 12.0436 > 0$ ， $r_{2}^{L} α_{2}^{L} - (b_{2}^{U} - r_{2}^{L} γ_{2}^{L}) M_{1} \approx 9.5794 > 0$ 即(H)成立。根据定理B，系统(12)永久持续生存,数值模拟图也支持这一论断(图1)。然而，

$r_{1}^{L} α_{1}^{L} - (b_{1}^{U} - r_{1}^{L} γ_{1}^{L}) M_{2} - c_{1}^{U} W_{1} (α_{1}^{L} + γ_{1}^{L} M_{2}) \approx - 45.8671 < 0,$

即(H₀)不成立，故我们无法借助定理A得到持久性的结论，因此我们的结论确确实实地改进了文献 [1]。

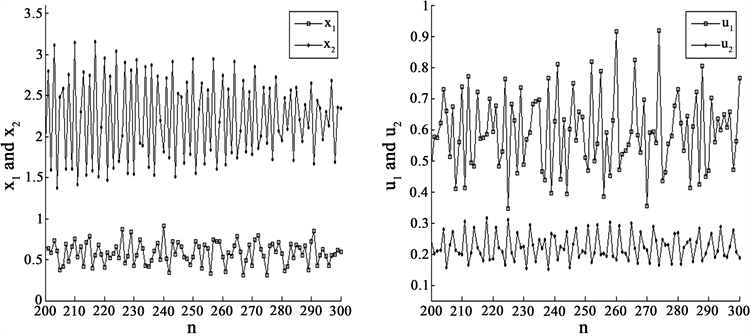
Figure 1. Numeric simulations of system (12) with the initial conditions ${(0 .3,0 .4,0 .7,0 .5)}^{T}$ , ${(1 .6,2 .1,1 .45,0 .2)}^{T}$ and ${(2 .4,3 .5,2 .21,1 .3)}^{T}$ , respectively

图1. 系统(12)在初始条件为 ${(0 .3,0 .4,0 .7,0 .5)}^{T}$ , ${(1 .6,2 .1,1 .45,0 .2)}^{T}$ 和 ${(2 .4,3 .5,2 .21,1 .3)}^{T}$ 下的数值模拟图

4. 小结

借助差分不等式，我们探讨了具Beddington-DeAngelis功能反应和反馈控制的离散非自治竞争系统，得到了一组比文 [1] 更弱的持久性条件，还明确了反馈控制变量不影响该系统的持久性的事实。数值模拟图展现了我们结论的正确性。

基金项目

2018年度福建省高等学校新世纪优秀人才支持计划；福建省自然科学基金资助项目(2019J01089)。

参考文献

参考文献

[1]	张杰华. 具反馈控制和Beddington-DeAngelis功能反应的离散竞争系统的概周期解[J]. 应用数学进展, 2020, 9(8): 1134-1145.
[2]	Chen, F.D., Chen, X.X. and Huang, S.Y. (2016) Extinction of a Two Species Non-Autonomous Competitive System with Beddington-DeAngelis Functional Response and the Effect of Toxic Substances. Open Mathematics, 14, 1157-1173. https://doi.org/10.1515/math-2016-0099
[3]	Yu, S.B. and Chen, F.D. (2019) Dynamic Behaviors of a Competitive System with Beddington-DeAngelis Functional Response. Discrete Dynamics in Nature and Society, 2019, Article ID: 4592054. https://doi.org/10.1155/2019/4592054
[4]	Zhang, J., Yu, S. and Wang, Q. (2020) Extinction and Stability of a Discrete Competitive System with Beddington-DeAngelis Functional Response. Engineering Letters, 28, 406-411.
[5]	余胜斌. 一类非自治连续型竞争系统的概周期解[J]. 福州大学学报(自然科学版), 2019, 47(3): 290-294.
[6]	Chen, F.D., Xie, X.D., Miao, Z.S., et al. (2016) Extinction in Two Species Nonautonomous Nonlinear Competitive System. Applied Mathematics and Computation, 274, 119-124. https://doi.org/10.1016/j.amc.2015.10.068
[7]	Chen, F.D., Gong, X.J. and Chen, W.L. (2016) Extinction in Two Dimensional Discrete Lotka-Volterra Competitive System with the Effect of Toxic Substances (II). Dynamics of Continuous, Discrete and Impulsive Systems Series B: Applications & Algorithms, 20, 449-461.
[8]	Yu, S.B. (2017) Extinction for a Discrete Competition System with Feedback Controls. Advances in Difference Equations, 2017, Article No. 9. https://doi.org/10.1186/s13662-016-1066-1
[9]	余胜斌. 具反馈控制和 Holling-III的修正Leslie-Gower捕食系统的持久性[J]. 延边大学学报(自然科学版), 2018, 44(1): 49-53.
[10]	余胜斌, 张杰华. 具时滞和反馈控制的修正Leslie-Gower离散系统的持久性[J]. 应用泛函分析学报, 2014, 16(3): 244-249.
[11]	王颖, 陈江彬. 具反馈控制和Holling-Ⅱ类功能性反应的修正Leslie-Gower捕食系统的持久性[J]. 福州大学学报(自然科学版), 2016, 44(2): 150-155.
[12]	Wang, L.L. and Fan, Y.H. (2008) Permanence for a Discrete Nicholson’s Blowflies Model with Feedback Control and Delay. International Journal of Biomathematics, 1, 433-442. https://doi.org/10.1142/S1793524508000369
[13]	Chen, F.D. (2008) Permanence for the Discrete Mutualism Model with Time Delays. Mathematical and Computer Modelling, 47, 431-435. https://doi.org/10.1016/j.mcm.2007.02.023

为你推荐

友情链接