1. 引言
蒸散发别名蒸腾蒸发量,是水文循环中降水到达地面后由液态或固态转化为气态又回到大气中去的过程。具体包含下垫面水分蒸发和植物表面和体内水分蒸腾,此过程不仅伴随着能量、水和碳系统的循环,还是水热循环的重要环节,主要受到温度、太阳辐射、相对湿度、风速等的影响。在全球范围内,水分收支会对天气和气候变化造成很大的影响,而青藏高原不仅能够阻挡西风气流,为我国长江流域、珠江流域等地区带来大量降水;还可以屏蔽冷暖气流,使我国受冬季风影响较小;还对我国的冬、夏季风具有促进作用,为我国夏季带来丰沛江水,冬季带来较强的季风环流。研究表明,青藏高原是影响整个东亚地区各种异常灾害天气的气候敏感区,对我国、亚洲、北半球乃至全球的天气、气候和环境变化有着及其重要的影响。由于自然因素和人类活动的共同作用,青藏高原环境发生了明显的变化,比如:冰川加速融化、冻土加速消融、高寒草甸退化、植被生长期提前等等。青藏高原是气候变化的敏感区和脆弱区,因此研究变暖最为显著阶段青藏高原蒸散的变化及其对气候变化的响应具有重要的科学意义和应用价值。一直以来,青藏高原气候变化研究都是科学家关注的焦点问题,作为气候变化的重要组成也倍受重视 [1]。青藏高原是为我国气候多样化做出了突出贡献,因此研究青藏高原的蒸散发势在必行。
青藏高原被誉为“世界第三极”,其所造成的环境后果对整个地球,特别是欧亚大陆的环境和生态系统是一场灾难。最近,中国科学院编写了一份科学报告,以评估西藏高地的环境变化,专家组消耗了超过100名国内外专家的资金。对过去2000年至今后100年环境变化影响所做的分析为现在的首脑会议的环境保护和生态建筑提供了科学依据。报告指出,全球变暖和潮湿的温度导致大溪地高原气候变化特别严重,水循环受到气候变化的影响。在过去2000年间,绿色高原内的温度变化不一样,但是终将变化无常。20世纪,全球气温上升超过以往至少2000年以来平均水平的两倍。与此同时,在青藏高原的南端和北端也存在着明显的不同,北部则呈上升趋势,而南部则呈下降趋势。同时,科学家们预测今后和未来青藏高原气候将会继续因为变暖和潮湿而受到影响 [2]。
近几十年根据青藏高原低纬度和高地势,空气密度小,太阳辐射强,日照时间长,体积偏大的特点,使其形成了冬天不寒冷,夏季温凉,气温年差较大,日较差大,高原的高原季风气候,青藏高原全体的气温是远远低于周边地区的温度,且存在两个明显的气温低值中心,昆仑山地区和祁连山的附近,柴达木盆地地区是高值中心 [3]。在降水方面,降水地区降雨量急剧下降的是青藏高原上唐古拉山地区东部和雅鲁藏布大峡谷,而河谷地区降雨量急剧上升的是西藏高原的西南部和南部地区的西宁高原东侧 [4]。此外,年降水量明显不同的是青藏高原北部和南部之间,降水逐渐增大,高原的东南西北的主要中心地区的降水量介于雅鲁藏布江地区和二级数据中心,在四川西部的高原地区。高原东部降水量由东南向西北下降,西藏东部和四川西部降水量高,柴达木盆地降水量低;降水场可分为八个分区,即西藏东部和四川的西部、南部高原西藏上部的平原、河谷、青南高原区、柴达木盆地区、四川西部高原北部、青海高原的东南部和青海东北部。蒸散发在高原气候系统中起着重要的作用,季风环流和西风环流共同作用 [5]。
近年来,蒸散受到全球变化科学研究的高度关注主要是因为它在土壤–植物–大气系统中的重要的纽带作用。生态系统蒸发与净生产力密切相关,由此产生的长期变化不仅影响到碳循环,而且也影响到水循环,水循环占全球陆地降雨量的60%~65%。蒸散是气候系统的重要过程之一,是水、能源和碳循环的核心。目前许多地面观测蒸散的方法分散在世界各地,如:① 仪器测定法。应用蒸散计(内装生长着植物的柱状土样仪器或实测种植作物整段土体的蒸散量)定期测定土壤水分损失量。② 经验公式法包含涡度相关法、液流法、波文比法、蒸渗仪法和闪烁仪法等。用数理统计方法,确定蒸散量与各种气候要素的相关关系,建立计算蒸散量的经验方程。③ 水分平衡法。在地下水较深,在根分布层无水分补给的情况下,通过定期测定降雨量和土壤水分含量确定蒸散量。④ 湍流交换法。通过测定近地面层的水汽梯度和湍流系数以计算水分的垂直通量,从而确定蒸散量。⑤ 热量平衡法。通过测定地表热量收支的各分量以确定消耗于蒸散的热量。⑥ 综合法。综合应用热量平衡方程和湍流交换方程计算可能蒸散量,再用可能蒸散量和土壤水分含量及植被状况参数建立函数关系,计算实际蒸散量。⑦ 蒸发互补法大尺度的模型模拟方法 [6]。陆面蒸散主要受气候因子如:温度、相对湿度、风速、日照常数等控制,并受植被和土壤性质以及土壤可供水量的制约,气候变化对于一个流域中敞露的水面、裸土及植被的蒸发及散发的影响都是截然不同的 [7]。
从古至今,人们对蒸散发的估算和研究就从未停歇。1963年,Bouchet研究了实际蒸发量、潜在蒸发量和潜在蒸发量之间的互补性,提出了众所周知的蒸发互补性原理,从而成为标志着蒸发研究史上的一个转折点。不需要很难获得水文和土壤数据,而利用传统气象站的数据直接估计实际蒸发量就足够了,这导致了国内外研究人员的深入研究和许多模型的出现。基于这一理论,如AA模型、CARE模型、GG模型等,最近几年许多学者又发展了互补性理论。韩松俊等提出用非线性互补关系模型来评估潜在蒸散发量与实际蒸散发量的关系;受该模型启发,Brutsaert通过对实际蒸散发与潜在蒸散发的比值和表观潜在蒸散发与潜在蒸散发的比值设定物理约束,并且将三个蒸散发表述为归一化变量的三次多项式,提出广义互补原理 [8];Craigo等人修订了Burtsaert互补性和相关性的一般原则,并根据美国关于水深和土壤降水的数据测试了经修订的模型,然后提出了一个仅基于互补理论的线性扩展。Szilagyi等人从单一估计公式P-T中推断一个无校准的CR模型和一个阿尔法参数模型,同时考虑到使用水量平衡数据的局限性。该模型具有最小的数据要求,而阿尔法参数的计算与该模型无关,该模型的真实蒸发扩散可以作为对大陆潜在热流的未校准估计。越来越多的科学家参与了基于广泛补充扩散模型的蒸汽传播研究,并取得了许多科学成果。
本文将青藏高原作为研究区域,选用互补理论的计算模型通过对近三十年的气象数据资料的计算,得到实际蒸散量,并对蒸散量随时间和空间的变化趋势进行分析,同时为水分收支对气候的影响的分析提供科学依据。截止到现在对于青藏高原上蒸散发的研究非常有限,对西藏高原蒸发的研究非常有限,有些研究侧重于高原蒸发的趋势,但仅限于独立地点或估计地点大概简单温度蒸发计算,其结果是不科学的。比如Tateshi和Ahn 1995年根据卫星测量的蒸发量得出的估计数没有考虑到湿度和风速。但是,这两个因素对于高原的高纬度很重要,因此研究不完整;还有Thomas对高原1951~1993年参照蒸散发的研究表明高原东部蒸散发既有增加又有减小的趋势,研究结果呈现矛盾使得整个研究不严谨;Thomas和Chen的研究指出青藏高原雅鲁藏布江河谷1954~1993年7月的参照蒸散发呈现速率为7.5 mm/10年减小趋势,此研究结果在误差范围内是可以认为参考蒸散发是没有变化的 [9]。因此,对于青藏高原上蒸散发变化的研究仍然比较粗略存在许多不足。进一步科学、严谨、全面的研究蒸散发需要我们不断地去分析,去探索,去研究。
2. 资料与方法
2.1. 研究区域概况
青藏高原是中国最大、世界海拔最高的高原。大部分在中国西南部,包括西藏自治区和青海省,四川省西部,新疆维吾尔自治区南部以及甘肃和云南部分地区。整个青藏高原也包括不丹、尼泊尔、印度、巴基斯坦、阿富汗、塔吉克斯坦和吉尔吉斯斯坦的部分地区,总面积250万平方公里。在我国境内面积240万平方公里,平均海拔4000~5000米,有“世界屋脊”和“第三极”之称 [10]。青藏高原从喜马拉雅山以南到昆仑山以北,从阿尔金山到祁连山,从西部的帕米尔山到喀喇昆仑山,东部和东北部与秦岭西部和黄土高原相连,介于北纬26˚00'~39˚47',东经73˚19'~104˚47'之间。它是东亚、东南亚和南亚许多河流的发源地;高原上有许多湖泊,包括青海湖,青藏高原是世界上海拔最高、垂直地带性最强的自然地理单元这个高原腹地年平均气温低于0℃;大面积最暖月份平均气温低于10℃;高原不同生态系统在水热方面与其他生态系统有很大不同。在全球气候变化条件下,其水热条件也有不同的变化趋势。因此,青藏高原蒸散量的研究对于研究青藏高原陆地生态系统和水循环的气候变化机制具有重要意义。研究区如图1。
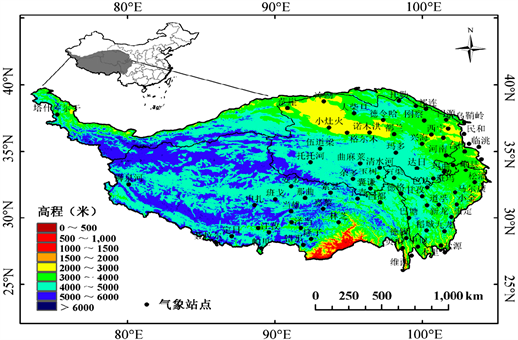
Figure 1. Sketch map of the Tibetan Plateau [11]
图1. 青藏高原示意图 [11]
2.2. 资料概况
气象数据包括青藏高原所属省份青海省和西藏的62个测站的1982年到2011年的日平均气温、最大温度、最小温度、相对湿度、气压、平均风速、日照常数。数据来源于青藏高原科学数据中心,其中心不仅提供了气象数据还提供了测站的经度、纬度信息,并且数据都是经过质量控制的。
我的数据是《中国地面气候资料日值数据集》,通过查阅参考文献的到自己所需要的是青藏高原所有测站的经度、纬度、海拔高度、平均气温、平均风速、相对湿度、日照时数这些数据。此时我所需要做的就是把所有月数据中的关键数据提取出来,由于是全国的所有测站数据,文件过大,人为费时费力所以采用MATLAB进行数据的整理。然后用得到的关键数据运用FORTRAN程序语言进行计算。得到实际蒸散量然后进行时间和空间的特征分析。
2.3. 研究方法
Bouchet (1963)首先提出的互补原理为自然景观中蒸发量的估算提供了框架,互补理论首先讨论了蒸散量中三者之间的关系,即实际蒸散量E、潜在蒸散量Epo、表观潜在蒸散量Epa。第一种当地面有充足的水分时,能量是唯一的限制条件,此时
(1)
当地表不再有足够的水供应时,E会减小此时的
,三者之间的关系是
(2)
设
,
,当
,
时
则
(3)
在潜在条件下:
。
则
(4)
由上综合可得
(5)
由幂函数的多项式可得:
(6)
考虑到以下四个边界条件:1) 在非常潮湿的条件下表明
为
。2) 当
接近零时,或者是由于真正的潜在蒸发消失,或者是因为在干旱增加的条件下
增大,在这种情况下也将接近零;因此
。3) 实际蒸发量E除表征地表水的可用量外,还取决于与
相同的变量。随着
趋于
,E也是如此,并且逐渐地,E变得相对较少地受到水的可利用性的影响,而受到其他控制变量以
的方式的影响更大。结果,当可用水量增加时,蒸发量dE的任何变化将变得与
相同。实际上,实验研究也表明
时
最终可得出
。4) 随着干旱的增加,y必然比x更接近于零,因此如果根据(2)两者都达到零,则对于给定的增量dx,dy必然会更小;因此,极限为
可以要求
。
这四个条件可以总结如下:
(7)
根据幂函数的定义,满足上面四个边界条件的多项式是一个三次多项式。
此时⑥式中的
,最终得到
,
,
,
。
得:
(8)
讲定义了y、x的式子代入,得到
(9)
1963年Bouchet最初提出的互补函数是
,而1998年Brutsaert和Parlange提出了互补函数的扩展
,此时当
时与实际变量的无量纲术语的关系最佳。此时不难看出他们仅仅满足一个边界条件,实际上在干旱条件下还会消失,与此同时当
或者
时会出现负蒸发,与实际不相符合这就更加验证了满足四个边界条件的互补理论模型才是最精确的。
目前Brutsaert和Stricker [1979]的对流干度法的方式应用于实际问题。因此潜在蒸发量可以用泰勒和普利斯特里方程来表示,即:
(10)
表观潜在蒸散量可以用Penman [1948, 1956]的开放水蒸发方程,即:
(11)
其中
(12)
最终得到实际蒸散发的公式如下:
(13)
理论公式中各个参数的意义
其中
普利斯特利和泰勒参数,表面粗糙度参数
和
,位移高度
,这四个都是可调参数,原则上可以从有关表面性质的现有信息中进行估算。但是,当某些蒸发测量可用时,可以通过用这些数据进行校准直接确定它们。在本文计算中要直接确定其值
,
,
。
是饱和水气压关于温度变化的斜率,其中马格努斯(Magnus)饱和水汽压的计算公式如下:
(14)
对它进行关于温度t (K)求导数就得到了
的计算公式如下所示:
(15)
而实际水汽压则需要借助相对湿度和饱和水汽压来计算:
(16)
指相对湿度;
指的是干湿常数,在这里使用彭曼公式:
(17)
其中p (hpa)指的是本站气压。指可用能量通量:
(18)
根据基尔霍夫辐射定律,其中
是太阳净辐射,G是青藏高原土壤热通量。
(19)
已知
(20)
(21)
,
,
是太阳高度角,H (m)是海拔高度,tmax (K)是最高温度,tmin (K)是最低温度,n (h)是日照时数,N (h)是可照时数。
指地理纬度,
指太阳赤纬,tt指地方时 [12]。
3. 研究结果
3.1. 蒸散发随空间变化趋势
1982~2011年,我国青藏高原地区多年平均蒸散量出现在748 mm到1412 mm,最大值出现在西藏的日喀则(55,578),最小值则出现在青海的冷湖(52,602)这里。根据年平均蒸散量等值线图(图2)发现青藏高原地区蒸散量呈现东高西低、南高北低的格局,具有明显的空间分布特征。根据干湿年蒸散量的对比(表1)发现青藏高原蒸散的空间分布与降水梯度分布接近,蒸散发最小的区域主要分布于藏北高原和巴颜克拉山以北,该区域广布高原降水量较少、土壤湿度低;蒸散最大的区域主要分布在藏南雅鲁藏布江及其支流流经的谷地和藏东横断山脉高山深谷的地区 [13]。
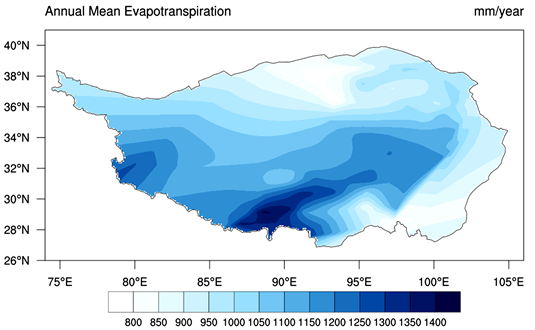
Figure 2. Annual average evapotranspiration of each station in the Tibetan Plateau in the three decades of 1982~2011 (unit: mm)
图2. 1982~2011年三十年青藏高原各站点的年平均蒸散量(单位:mm)

Table 1. Distribution comparison of actual evapotranspiration in dry and wet years from 1982 to 2011
表1. 1982~2011年干湿年实际蒸散量分布对比
3.2. 季节平均蒸散时空变化规律
本次研究采用气象划分法划分四季。本文对青藏高原月平均蒸散量(图3)进行了统计发现我国1982~2011年的季节平均蒸散空间分布呈现比较明显的变化,由于缺乏站点,沙漠和戈壁西北部地区没有蒸散量,西藏青藏高原北部和巴颜喀拉山北部的总体蒸散值低于其他地区,藏南的雅鲁藏布江及其支流、藏东横断山脉的高山深谷的蒸发蒸腾量值均高于其他地区。就季节平均蒸散空间分布规律而言,夏季平均蒸散量大于冬季。最大值出现在夏季太阳的转角处,最小值出现在冬至,类似于青藏高原降水的季节性分布。
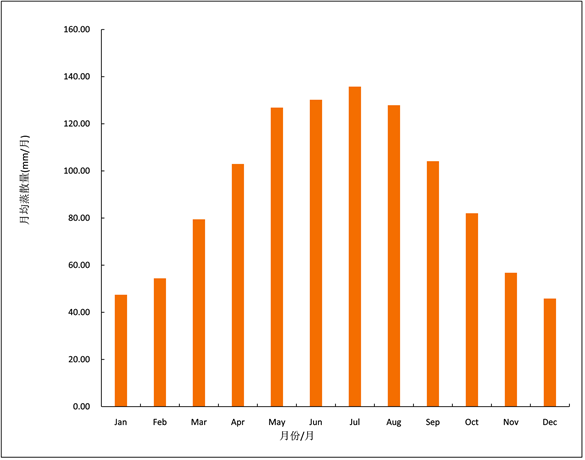
Figure 3. Average monthly evapotranspiration of the Qinghai Tibet Plateau of 1982 to 2011
图3. 1982~2011年青藏高原月平均蒸散量
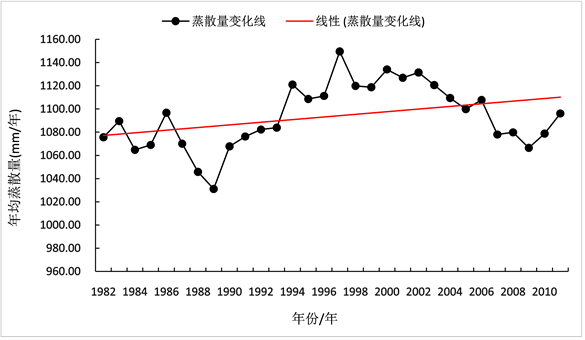
Figure 4. Mean and trend of evapotranspiration over the Tibetan Plateau from 1982 to 2011
图4. 1982~2011年青藏高原整体蒸散量均值以及趋势图
由图4可以看出,由于自然因素和人类活动的共同影响,青藏高原环境发生了显著变化:冰川融化加速、冻土消融加快、高寒草甸退化、植被生长期提前等。也会造成青藏高原近几十年蒸散量随之增长的趋势,自2000年以来,国家投入巨资开展生态修复,先后实施了一批生态环境保护与建设重大工程,如退耕还林还草、退牧还草、天然林保护、防护林体系工程等。随着生态工程的实施,部分区域的植被状况得到了改善,因此青藏高原蒸散量在1997~2005年相对稳定呈现一种下降的趋势。
3.3. 蒸散量变化趋势的空间分布特征
对青藏高原每个测站1982~2011年的蒸散数据和时间中的日期两个变量做线性回归分析,得到线性回归系数,并对它进行差值分析得到图5。我们知道线性回归函数的斜率代表的是变化的快慢,在青藏高原的北部系数为正值,说明了这三十年来实际蒸散量随时间在逐步增大,但是在青藏高原的南部少数测站出现了线性负值,即随着时间的推移实际蒸散量在逐渐减小。但是从总体看出实际蒸散量与时间的线性回归函数的斜率是增大的,也就说明了三十年来青藏高原的实际蒸散量呈现一种上升的趋势。
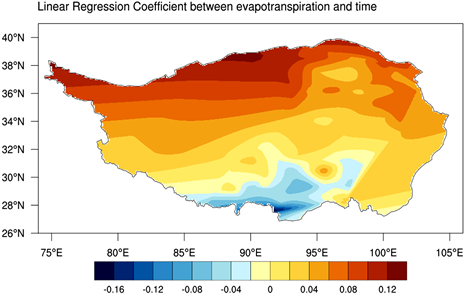
Figure 5. Spatial distribution of actual evapotranspiration over the Tibetan Plateau during three decades from 1982 to 2011
图5. 1982~2011三十年间青藏高原实际蒸散量变化趋势空间分布图
3.4. 影响因素分析
3.4.1. 环境因素的气候倾向率
对青藏高原1982~2011年的温度、相对湿度、平均风速、日照常数分别和实际蒸散量做线性回归分析,得到他们各自的线性回归系数,也就是我们这里的气候倾斜率。然后对他们分别进行分级处理,得到图7的四幅子图。气候倾斜率代表的是各个环境要素对当地气候的影响程度。
从青藏高原温度的气候倾斜率(图6(a))中可以观察到温度对青藏高原的气候起到一定的正向影响,即:温度的升高会使得气候要素值升高,反之亦然。局部来说青藏高原的北部大部分区域收到温度的影响程度较大,影响最小的区域在青藏高原是西南一侧三个测站所属区域。并且影响程度整体呈现出一种由北向南逐级递减的趋势。越往南走实际蒸散量受到温度的影响越小。但是整体呈现出的还是一种实际蒸散量增大的态势。
从青藏高原相对湿度气候倾向率(图6(b))中可以看出青藏高原的西南部地区气候受到相对湿度的正面影响,以为气候要素随着相对湿度会增加,但是在青藏高原的北部和东部部分地区则受到相对湿度的负面影响,也就是相对湿度增加,实际蒸散量反而会下降。并且相对湿度对气候的影响程度呈现出一种由西南向东北递减的趋势。
从青藏高原平均风速的气候倾向率(图6(c))中可以观察到平均风速对于气候的影响起到了逆向的作用,即:平均风速增大,实际蒸散量反而减少。并且从东北部到西南部影响程度依次减小,北部主要吹西北风,由于西北风属于干冷空气它会使得水汽大量蒸发,因而北部较之南部蒸散量下降幅度较大。
从青藏高原日照常数的气候倾向率(图6(d))中观察到日照常数对于气候倾向于一种正面影响,且在太阳辐射比较强的北部地区,蒸散量随日照常数增加幅度较大。
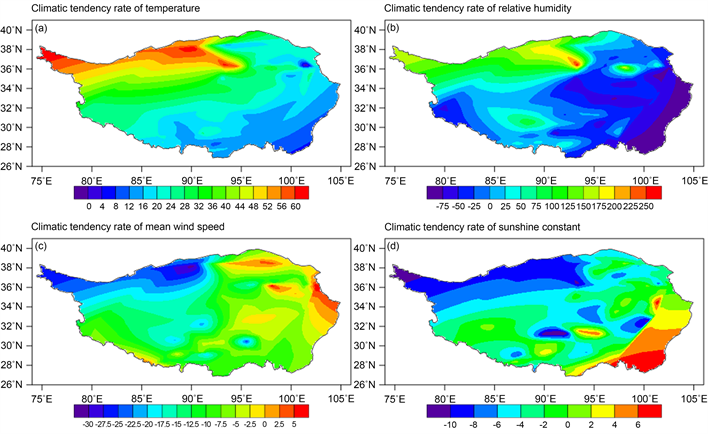
Figure 6. Climate tendency rate of various environmental factors in the Tibet Plateau from 1982 to 2011
图6. 1982~2011年青藏高原各个环境因子气候倾向率空间分布特征
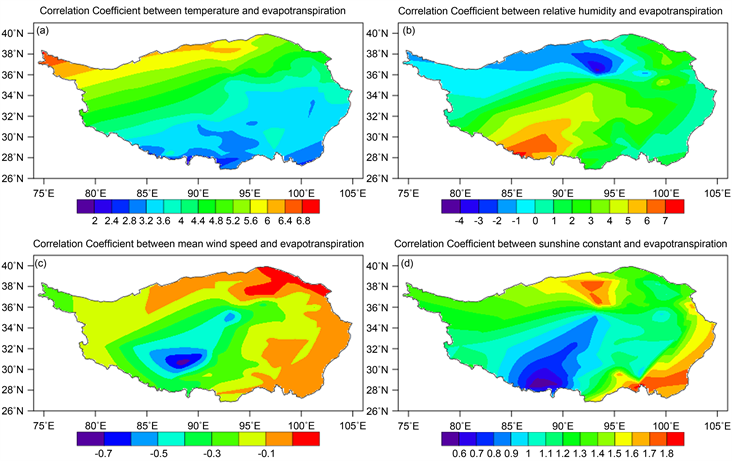
Figure 7. Spatial distribution of correlation coefficients between various environmental factors (Average temperature a; Relative humidity b; Average wind speed c; Sunshine constant d) and Actual evapotranspiration in the Tibet Plateau from 1982 to 2011
图7. 1982~2011年青藏高原各个环境因子(平均温度a;相对湿度b;平均风速c;日照常数d)与实际蒸散量相关系数空间分布图
3.4.2. 实际蒸散量与温度、相对湿度、平均风速、日照常数的相关性
相关系数反映的是实际蒸散量与温度、相对湿度、平均风速、日照常数之间的密切程度。当相关系数大于零时,实际蒸散量随着环境因子的增加,实际蒸散量呈上升趋势;相关系数小于零,则相反。相关系数的绝对值越大,说明实际蒸散量与环境因子的关系越密切。
从图7可以观察到平均风速与实际蒸散量成负相关关系,也就是随着平均风速的增加实际蒸散量呈下降趋势,其余环境因子和实际蒸散量呈正相关关系。相比较过后,发现相关系数绝对值较大的当属温度和实际蒸散量这一项,说明温度和实际蒸散量的关系更为密切。换句话来说就是温度对实际蒸散量的贡献较大。
4. 结论
根据本文分析青藏高原蒸散量时空分布特征及温度、相对湿度、平均风速、日照时数等环境因子对其的影响。结果表明,1982~2011年青藏高原多年平均实际蒸散量值为1093.77 mm/年,呈现出明显的空间分布特征,具体位置实际蒸散量最大值一般分布在青藏高原的东南部地区,即:雅鲁藏布江以南以及它的支流分布区如澜沧江、金沙江,而最小值地区分布在藏北高原一带和巴颜克拉山以北以及西北部地区,青藏高原西北部蒸散量为零,原因是由于本地区地形问题使人类无法观测到具体气象要素值;青藏高原实际蒸散量存在年、月和季节的时间变化,实际蒸散量夏季最大,之后依次是春季、秋季、冬季,且全年除冬季外都表现出明显的上升趋势,趋势变化最显著的是秋季。青藏高原三十年来实际蒸散量随时间在增加。青藏高原实际蒸散量与温度的关系密切,受到温度影响较大;且随平均风速的增加而减少,相对湿度和日照常数对实际蒸散量的影响是正向的,但是影响程度不如温度高。
5. 展望
本文抛开原有很难获得的水文和土壤数据,直接应用气象数据基于广义互补理论中边界条件的实施产生的物理约束,在完全饱和的表面水分状态允许下制定(E-Epo)之间的互补关系和(Epa-Epo)作为一个三次多项式的非线性函数,来估计实际蒸散量进而对青藏高原的气候特征进行分析。它不仅是对Bouchet [1963]最初提出的线性函数的推广,也是后来Brutsaert [1998]在只有一个约束的基础上对其进行线性扩展的又一大进步。广义互补理论相比于以往互补概念和非互补概念最大的优势是,在极其干旱的条件下具备更真实的性能。后面我会将广义互补理论非线性函数加入一个可调函数采用四次方程的形式,通过校准来估计实际蒸散量值,以确保得到更精确的估计值来进一步探索青藏高原气候的奥秘 [14]。