一类微驱动器的复合控制及稳定性分析

Stability Analysis for a Class of Micro Actuator under the Compound Control

摘要: 考虑一类基于微驱动器的微分方程摩擦模型，对微驱动器的动态方程进行重构，得到等价状态空间模型。根据该模型，提出了一种新的包括前馈控制、PID控制和径向基神经网络控制的复合控制方法。通过构造合适的李雅普诺夫函数，证明了系统在平衡点是渐近稳定的，且跟踪误差渐近收敛到零。

Abstract: The difference equation model of micro actuator is considered in this paper. An equivalent state space model is derived from the dynamic equation of micro actuator. According to the model, a new compound control method, including feed-forward control, PID control and radial basis network control, is proposed. The stability of the new control method is proved through constructing ac-ceptable Lyapunov function.

1. 引言

压电陶瓷驱动器是一种常见的微驱动器，在半导体制造 [1] [2]、生物医学 [3]、航天航空 [4] [5] 等高科技领域中得到了广泛的应用 [6] [7]。但是压电陶瓷存在着非线性 [8]、蠕变性和迟滞性 [9] 等不足，使得微位移机构的定位精度降低，瞬间响应速度变慢，给微驱动器的应用造成了一定的困难。国内外许多学者进行了大量的研究 [10] [11] [12]，采用了很多模型去模拟和研究微驱动器的迟滞特性。

在微驱动器控制算法的研究上，无论是开环控制还是闭环控制，电压驱动还是电荷驱动，要使微驱动器达到所需的定位精度及动态特性，都必须同一定的控制算法相结合。例如：PID控制、模型参考自适应控制、模糊控制以及将某两种方法结合起来的复合控制等。目前针对复合控制，国内外许多学者已经进行了广泛的研究与探索。例如：文献 [13] 提出了逆Bouc-Wen前馈控制与反馈控制相结合的复合控制算法，用于改善压电陶瓷驱动器对目标轨迹的跟踪性能；文献 [14] 设计了基于径向基函数(RBF)神经网络的复合自抗扰方法，提高了系统的动态性能和稳态精确度；文献 [15] 利用BP神经网络迟滞逆模型与专家模糊控制相结合的复合控制方法，有效地消除迟滞对定位平台的定位精度影响。这些研究均表明复合控制结合多种控制算法的优点后，在动态过程控制、鲁棒性控制和干扰抑制方面具有明显的优势。

由于压电陶瓷的迟滞特性较为复杂，难以获取准确的数学模型。另外，在精密定位过程中存在外部扰动、摩擦力等也影响了定位的精度。而径向基神经网络具有自学习，自校正的人工智能特点，经过训练后即使输入信号不在训练样本中，也能以任意精度逼近非线性函数，具有很强的鲁棒性。传统的前馈-PID复合控制 [16] 对外部扰动、摩擦力等影响不敏感，因此将径向基神经网络与传统的前馈-PID复合控制结合，为克服微驱动器的迟滞非线性提供一种新的思想。

本文在微分方程摩擦模型 [17] [18] [19] 的基础上，提出了一种基于径向基神经网络的复合控制方法，以消除微驱动器的迟滞非线性对精密定位精度的影响，提高系统定位精度。该方法利用前馈控制器、PID控制器以及径向基神经网络适配器对微驱动器进行复合控制。基于该控制方法给出了系统稳定所需的条件，通过构造合适的李雅普诺夫函数，证明了系统在平衡点是渐近稳定的，且跟踪误差渐近收敛于0。

2. LuGre摩擦模型的问题描述

LuGre摩擦模型 [17] [18] [19] 将两个不规则的接触面想象成弹性刚毛的接触，当施加切向力时，刚毛就会像弹簧一样变形，刚毛所产生的阻力便是摩擦力。而刚毛的平均形变定义为

$\stackrel{\dot{}}{h}=\stackrel{\dot{}}{x}-\frac{\left|\stackrel{\dot{}}{x}\right|}{g\left(\stackrel{\dot{}}{x}\right)}h$ (1)

其中，h是接触面之间弹性刚毛的平均形变， $\stackrel{\dot{}}{h}$ 是平均形变的一阶导数， $\stackrel{\dot{}}{x}$ 是输出位移对时间的一阶导数，表示两个接触面的相对速度，函数 $g\left(\stackrel{\dot{}}{x}\right)$ 代表Stribeck效应曲线。

由刚毛变形所产生的摩擦力描述为：

$F_h={\sigma }_{0}h+{\sigma }_1\stackrel{\dot{}}{h}+{\sigma }_2\stackrel{\dot{}}{x}$ (2)

其中， $F_h$ 是迟滞摩擦力， ${\sigma }_0$ 、 ${\sigma }_1$ 、 ${\sigma }_2$ 是控制参数。

根据牛顿第二定律，压电陶瓷驱动器的动态方程为：

$m\ddot{x}+c\stackrel{\dot{}}{x}+kx+F_h=Tu$ (3)

其中，m是压电陶瓷驱动器的有效质量，c是有效阻尼系数，k是有效机械刚度，x是压电陶瓷驱动器的输出位移， $\stackrel{\dot{}}{x}$ 和 $\ddot{x}$ 分别是输出位移对时间的一阶和二阶导数，T是输入控制系数，u是压电陶瓷驱动器的驱动电压。

由于LuGre摩擦模型存在迟滞摩擦力 $F_h$，所以压电陶瓷驱动器表现为迟滞非线性，导致它在实际工程应用中严重影响了它的定位精度。

3. 模型的重构及控制器的设计

对于上述精密运动控制问题，为了克服压电陶瓷驱动器的迟滞非线性对驱动精度的影响，提高系统定位精度，本文提出了一种基于径向基神经网络的压电陶瓷驱动器复合控制方法。

将压电陶瓷驱动器的动态方程改写为：

$\ddot{x}=-\frac{c}{m}\stackrel{\dot{}}{x}-\frac{k}{m}x-\frac{1}{m}{F}_h+\frac{T}{m}u$ (4)

假设1：压电陶瓷驱动器的期望位移 $x_d$ 和输出位移x是连续的，关于时间t是二阶可导的。

由于跟踪误差e定义为：

$e=x_d-x$ (5)

所以跟踪误差e关于时间t的二阶导数为：

$\begin{array}{l}\ddot{e}={\ddot{x}}_d-\ddot{x}\\ ={\ddot{x}}_d+\frac{c}{m}\stackrel{\dot{}}{x}+\frac{k}{m}x+\frac{1}{m}{F}_h-\frac{T}{m}u\\ ={\ddot{x}}_d-\frac{c}{m}{\stackrel{\dot{}}{x}}_d+\frac{c}{m}\stackrel{\dot{}}{x}+\frac{c}{m}{\stackrel{\dot{}}{x}}_d-\frac{k}{m}{x}_d+\frac{k}{m}x+\frac{k}{m}{x}_d+\frac{1}{m}{F}_h-\frac{T}{m}u\\ =-\frac{c}{m}\stackrel{\dot{}}{e}-\frac{k}{m}e-\frac{T}{m}u+\frac{1}{m}{F}_h+\frac{T}{m}\left(\frac{m}{T}{\ddot{x}}_d+\frac{c}{T}{\stackrel{\dot{}}{x}}_d+\frac{k}{T}{x}_d\right)\end{array}$ (6)

令：

$-\frac{T}{m}H\left(x\right)=\frac{1}{m}{F}_h$ (7)

其中， $H\left[x\left(t\right)\right]$ 是未知的非线性光滑函数。

于是：

$\ddot{e}=-\frac{c}{m}\stackrel{\dot{}}{e}-\frac{k}{m}e-\frac{T}{m}u-\frac{T}{m}H\left(x\right)+\frac{T}{m}\left(\frac{m}{T}{\ddot{x}}_d+\frac{c}{T}{\stackrel{\dot{}}{x}}_d+\frac{k}{T}{x}_d\right)$ (8)

因为误差系统上串联一个积分器可以有：

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_0^{t}e\left(\tau \right)\text{d}\tau }=e$ (9)

所以所形成的新系统状态变量为 $x_1={\displaystyle {\int }_0^{t}e\left(\tau \right)\text{d}\tau }$， $x_2=e$ 和 $x_3=\stackrel{\dot{}}{e}$。

再定义 $X={\left[\begin{array}{ccc}{x}_1& x_2& x_3\end{array}\right]}^{\text{T}}$，然后将式(8)转化为等价状态空间表达式，有：

$\stackrel{\dot{}}{X}=AX+Bu+BH\left(x\right)+B\left(\frac{m}{T}{\ddot{x}}_d+\frac{c}{T}{\stackrel{\dot{}}{x}}_d+\frac{k}{T}{x}_d\right)$ (10)

其中， $A=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& -\frac{k}{m}& -\frac{c}{m}\end{array}\right]$， $B=\left[\begin{array}{c}0\\ 0\\ -\frac{T}{m}\end{array}\right]$。

此外，微驱动器的控制电压u可取为：

$u=u_1+u_2+u_3$ (11)

其中 $u_1$， $u_2$， $u_3$ 分别设计如下：

1) 前馈控制器输出的电压信号 $u_1$ 为：

$u_1=-\frac{m}{T}{\ddot{x}}_d-\frac{c}{T}{\stackrel{\dot{}}{x}}_d-\frac{k}{T}{x}_d$ (12)

2) 系统的PID控制部分为：

$\stackrel{\dot{}}{X}\left(t\right)=AX\left(t\right)+Bu\left(t\right)$ (13)

所以确定PID控制器输出的电压信号 $u_2$ 为：

$u_2=KX=k_p{x}_1+k_i{x}_2+k_d{x}_3=k_p{\displaystyle {\int }_0^{t}e\left(t\right)\text{d}t}+k_{i}e\left(t\right)+k_d\stackrel{\dot{}}{e}\left(t\right)$ (14)

其中， $K={\left[\begin{array}{ccc}{k}_p& k_i& k_d\end{array}\right]}^{\text{T}}$， $k_p$ 是比例系数， $k_i$ 是积分时间常数， $k_d$ 是微分时间常数。

对式(13)求解，有唯一的最优控制为：

$u_2=-R^{-1}{B}^{\text{T}}PX\left(t\right)$ (15)

其中，正定对称矩阵P是黎卡提(Riccati)方程的解，

$A^{\text{T}}P+PA+PB{B}^{\text{T}}P+Q=0$ (16)

并且，Q是非负定对称矩阵( $Q=H^{\text{T}}H$ )，R是正定对称矩阵。

3) 神经网络补偿控制器的设计

为了进一步提高性能，引入径向基函数(RBF)对非线性迟滞进行建模，用RBF神经网络逼近系统径向基神的非线性部分，使余项线性化。

由于 $F_h$ 是迟滞非线性的，所以 $H\left[x\left(t\right)\right]$ 也是迟滞非线性的。理论和实践都已经证明神经网络只能逼近一对一映射或多对一映射关系，而对迟滞这样的多映射无能为力。因此，通过引入基本迟滞算子，将基本迟滞算子的输出与迟滞输入同时作为神经网络的输入，拓展了神经网络的输入空间，使得神经网络的输入与输出之间形成一对一映射，从而可以用神经网络逼近非线性迟滞 $H\left[x\left(t\right)\right]$。

如文献 [20] 的模型所示，本文所采用的基本迟滞算子(EHO)表达式为：

$f\left[x\left(t\right)\right]=\{\begin{array}{l}f\left(x_e\right)+{\left[x\left(t\right)-x_e\right]}^2,\stackrel{\dot{}}{x}\left(t\right)>0\\ f\left(x_e\right)-{\left[x_e-x\left(t\right)\right]}^2,\stackrel{\dot{}}{x}\left(t\right)<0\end{array}$ (17)

其中，x是基本迟滞算子的当前输入， $f\left[x\left(t\right)\right]$ 是基本迟滞算子的当前输出，基本迟滞算子所采用的单调曲线为 $f\left(x\right)=x^2$， $x_e$ 是位于 $x\left(t\right)$ 之前最近的一个输入极值，称为主导极值， $f\left(x_e\right)$ 是输入为 $x_e$ 时基本迟滞算子的输出。此时，基于EHO的迟滞模型，如图1所示。

由于引入基本迟滞算子扩展了非线性迟滞 $H\left[x\left(t\right)\right]$ 在神经网络的输入空间，在三维空间上将迟滞的多映射转化为一一映射，所以 $H\left[x\left(t\right)\right]$ 可以表示成一组基函数的线性组合，而RBF神经网络相当于用隐层单元的输出构成一组基函数，然后用输出层来进行线性组合，以完成逼近功能。故所用3层径向基神经网络的结构图，如图2所示。

Figure 1. Hysteresis model based on fundamental hysteresis operator

图1. 基于基本迟滞算子的迟滞模型

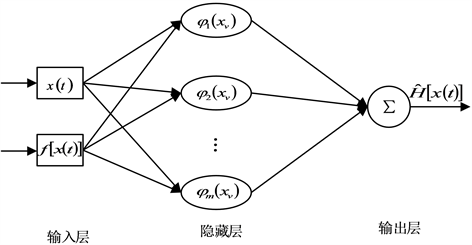
Figure 2. Structure diagram of radial basis function neural network

图2. 径向基神经网络结构图

第一层：输入层。输入向量为 $x_v={\left[\begin{array}{cc}x\left(t\right)& f\left[x\left(t\right)\right]\end{array}\right]}^{\text{T}}$。

第二层：隐藏层。径向基函数神经网络隐层节点的基函数的第i个隐藏节点的输出为：

${\phi }_i\left(x_v\right)=\exp \left(-\frac{{\Vert x_v-c_i\Vert }^2}{2{\sigma }_i^2}\right)/{\displaystyle \underset{i=0}{\overset{m}{\sum }}\exp \left(-\frac{{\Vert x_v-c_i\Vert }^2}{2{\sigma }_i^2}\right)}$ (18)

其中， $c_i$ 是第i个隐藏节点基函数的中心向量， ${\sigma }_i$ 是第i个隐藏节点基函数的宽度参数。

故非线性迟滞 $H\left[x\left(t\right)\right]$ 可以用径向基神经网络逼近为：

$H\left[x\left(t\right)\right]={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i{\phi }_i\left(x_v\right)}+\xi$ (19)

其中， ${\phi }_i\left(x_v\right)$ 是径向基函数， ${\omega }_i$ 是权重， $\xi$ 是输出层节点的阈值。

当 $\left|\xi \right|\le \epsilon$ 时，对 $H\left[x\left(t\right)\right]$ 的径向基神经网络估计为：

$\hat{H}\left[x\left(t\right)\right]={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i\left(x_v\right){\hat{\omega }}_i}$ (20)

其中， $\epsilon$ 是适当的误差精度， ${\hat{\omega }}_i$ 是径向基神经网络理想权重的估值。

因此，径向基神经网络适配器输出自适应调整后的电压信号表示为：

$u_3=-\hat{H}\left[x\left(t\right)\right]$ (21)

将式(11)、(12)、(15)和(21)代入式(10)，可以得到系统：

$\begin{array}{l}\stackrel{\dot{}}{X}=AX+B\left(u_1+u_2+u_3\right)+BH\left[x\left(t\right)\right]+B\left(\frac{m}{T}{\ddot{x}}_d+\frac{c}{T}{\stackrel{\dot{}}{x}}_d+\frac{k}{T}{x}_d\right)\\ =\left(A-B{R}^{-1}{B}^{\text{T}}P\right)X-B{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i}{\hat{\omega }}_i+B\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i}{\omega }_i+\xi \right)\\ =\left(A-B{R}^{-1}{B}^{\text{T}}P\right)X+B\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i}{\tilde{\omega }}_i+\xi \right)\end{array}$ (22)

其中， ${\tilde{\omega }}_i={\omega }_i-{\hat{\omega }}_i$。

综上，我们对模型进行了重构，并设计了复合控制方法，基于重构模型使得系统的稳定性分析更加方便。

4. 稳定性分析和误差分析

接下来考虑系统(10)的稳定性和跟踪误差问题。

定理1假设系统(10)中的未知函数 $H\left[x\left(t\right)\right]$ 采用径向基神经网络 $\hat{H}\left[x\left(t\right)\right]={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i\left(x,\stackrel{\dot{}}{x}\right){\hat{\omega }}_i}$ 来逼近，且假设径向基神经网络的理想权重的估值为：

${\stackrel{\dot{}}{\tilde{\omega }}}_i=-r{X}^{\text{T}}PB{\phi }_i$ (23)

令 $\gamma =\left[{\lambda }_{\min }\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right)-\eta {\lambda }_{\max }\left(PB{B}^{\text{T}}P\right)\right]$， $\alpha =\frac{1}{\eta }{\epsilon }^2$，当 $\Vert X\Vert >{\left(\frac{\alpha }{\gamma }\right)}^{1/2}$ 时，则系统(10)在平衡点是渐近稳定的，且跟踪误差e渐近收敛于0。

证明：根据式(22)，构造李雅普诺夫函数为：

$V=X^{\text{T}}PX+\frac{1}{r}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\tilde{\omega }}_i^2}$ (24)

显然V是正定的。

求李雅普诺夫函数关于时间t的导数如下：

$\begin{array}{l}\stackrel{\dot{}}{V}={\stackrel{\dot{}}{X}}^{\text{T}}PX+X^{\text{T}}P\stackrel{\dot{}}{X}+\frac{2}{r}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\tilde{\omega }}_i}{\stackrel{\dot{}}{\tilde{\omega }}}_i\\ =X^{\text{T}}\left(A^{\text{T}}P+PA-2PB{R}^{-1}{B}^{\text{T}}P\right)X+2X^{\text{T}}PB{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i{\tilde{\omega }}_i}+2X^{\text{T}}PB\xi +\frac{2}{r}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\tilde{\omega }}_i}{\stackrel{\dot{}}{\tilde{\omega }}}_i\\ =-X^{\text{T}}\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right)X+2X^{\text{T}}PB{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i{\tilde{\omega }}_i}+2X^{\text{T}}PB\xi +\frac{2}{r}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\tilde{\omega }}_i}{\stackrel{\dot{}}{\tilde{\omega }}}_i\end{array}$ (25)

由于 ${\stackrel{\dot{}}{\tilde{\omega }}}_i=-r{X}^{\text{T}}PB{\phi }_i$，从而 $\frac{\text{d}{\tilde{\omega }}_i}{\text{d}t}=\frac{\text{d}}{\text{d}t}\left({\omega }_i-\hat{\omega }\right)=-\frac{\text{d}\hat{\omega }}{\text{d}t}=-r{X}^{\text{T}}PB{\phi }_i$，于是有

$\begin{array}{l}\stackrel{\dot{}}{V}=-X^{\text{T}}\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right)X+2X^{\text{T}}PB{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\phi }_i{\tilde{\omega }}_i}+2X^{\text{T}}PB\xi +\frac{2}{r}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\tilde{\omega }}_i}{\stackrel{\dot{}}{\tilde{\omega }}}_i\\ =-X^{\text{T}}\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right)X+2X^{\text{T}}PB\xi \\ \le -{\lambda }_{\min }\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right){\Vert X\Vert }^2+2X^{\text{T}}PB\epsilon \end{array}$ (26)

因为

$2X^{\text{T}}PB\epsilon \le \eta X^{\text{T}}PB{B}^{\text{T}}PX+\frac{1}{\eta }{\epsilon }^2$ (27)

所以

$\begin{array}{l}\stackrel{\dot{}}{V}\le -{\lambda }_{\min }\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right){\Vert X\Vert }^2+\eta X^{\text{T}}PB{B}^{\text{T}}PX+\frac{1}{\eta }{\epsilon }^2\\ \le -{\lambda }_{\min }\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right){\Vert X\Vert }^2+\eta {\lambda }_{\max }\left(PB{B}^{\text{T}}P\right){\Vert X\Vert }^2+\frac{1}{\eta }{\epsilon }^2\\ =-\left[{\lambda }_{\min }\left(Q+PB{R}^{-1}{B}^{\text{T}}P\right)-\eta {\lambda }_{\max }\left(PB{B}^{\text{T}}P\right)\right]{\Vert X\Vert }^2+\frac{1}{\eta }{\epsilon }^2\end{array}$ (28)

当 $\Vert X\Vert >{\left(\frac{\alpha }{\gamma }\right)}^{1/2}$ 时，有

$\stackrel{\dot{}}{V}<0$ (29)

所以由李雅普诺夫第二方法知，设计的控制系统在原点平衡态是渐近稳定的，微驱动器的跟踪误差收敛到零点附近的一个小区域内，从而跟踪误差e渐近收敛于0。

5. 结束语

本文首先对系统进行重构，得到等价状态空间模型，并设计了前馈控制器、PID控制器以及径向基神经网络适配器对微驱动器进行复合控制。结合李雅普诺夫稳定性理论，分别确定了径向基神经网络理想权重的估值，给出了判断该控制系统稳定性的充分条件。它表明径向基神经网络理想权重选取适当的估值，通过调整径向基神经网络，使得系统在一定条件下渐近稳定，且跟踪误差e渐近收敛于0。所以该方法为了减小非线性迟滞特性所造成的不良影响，更好地发挥压电陶瓷的性能，开展对迟滞非线性系统的控制方法的研究，具有重要的理论意义和实际价值。为纳米定位、精密机械、主动振动消除、半导体制造及测试等应用提供可能。

基金项目

广东省自然科学基金项目(No.2018A030313505)，广州市科技计划项目(No.202002030448)。