1. 引言
乘法器电路是计算机系统、信号处理、密码系统、机器学习等众多现代数字电路系统中的重要组成部分,对其正确性进行验证是必不可少的一个环节 [1]。传统的模拟仿真技术与形式化验证方法是乘法器电路验证理论中最重要的两类验证方法。
传统的模拟仿真验证技术原理简单,可操作性强,应用范围广,但无法满足当前乘法器电路设计的巨大验证需求,取而代之的是形式化验证方法 [2]。例如,结合SAT求解方法与计算机代数方法验证乘法器 [3];使用优化乘数的SCA方法验证乘法器 [4] [5]。
近几年来,Gröbner基方法作为形式化验证方法的一种,越来越受到学术界的广泛关注与认同。
Ritirc等人提出的逐列检测方法 [6] 验证乘法器是使用C语言程序设计出相应的验证工具,并使用列式项序将电路逻辑变成切片,通过验证工具调用计算机代数系统Mathematica和Singular应用Gröbner基方法逐步验证电路每个切片的正确性进而验证乘法器的正确性。该方法在一定程度上降低了归约计算量,同时计算机代数系统Mathematica和Singular的加入,减少了手工操作,提高了其自动化程度。但在中间的约化过程中单项式数目急剧增加,验证耗费时间较长。因此,Ritirc等人在此成果之上又提出了加法器重写的方法 [7]。加法器重写即提取出电路中的加法器和半加器,约化其Gröbner基的内部变量。该方法大大的优化了Gröbner基方法,加快了验证速度,并可在有限时间内验证128位乘法器。
乘法器电路验证的Gröbner基方法逐步优化,但可供选择的计算机代数系统却只有Mathematica和Singular。由于各种操作系统优缺点不同,使用不同种方法搭配不同的代数系统,其验证结果和中间可能出现的情况未知,在一定程度上具有局限性。本文使用计算机代数系统Maple对Gröbner基方法给出了全新实现并在计算机上进行了对比实验,在某种程度上加快了乘法器验证速度,为后续验证方法的优化提供更多计算机代数系统的选择。
2. Gröbner基理论
本节介绍Gröbner基基础理论的关键内容,包括多项式理想、单项式序、Gröbner基定义和Gröbner基判定理想成员归属问题,相关证明和基础知识可以参考 [8] [9] [10]。
定义2.1 设k为任意一个数域,
是数域k上关于变量
的n元多项式环,如果非空子集
满足:
(1)
。
(2) 对任意的多项式
,
,都有
。
(3) 对任意的多项式
,
,都有
。
则称I是一个多项式理想。
任给有限个多项式
,令
易证
是
的多项式理想,
是
的生成元。
定义 2.2 设N是非负整数集合
单项式集合
,如果
上的一个序关系>满足:
(1) >是一个全序。
(2) >是一个良序。
(3) 若
,对所有
,都有
。
则序关系>是单项式序。
多项式环
中单项式序概念是一个基本概念。给定序关系后,可以将任一多项式 各项按序的大小惟一排列,保证n元多项式除法得到的余式是惟一的。单项式序包括字典序、分级字典序和分级逆字典序等。本文介绍字典序,其他类型项序可以参考 [9]。
定义2.3 对单项式
,规定
,如果
的从左向右第一个非零分量为负数,称这个序为字典序,记为
。
定义2.4 设I是
的多项式理想。
表示
的首项,
是I的所有元素关于字典序
的首项生成的理想,若存在I的有限子集
满足
则G是I的Gröbner基。
每个多项式理想都有一个Gröbner基,给定多项式理想的任意一个基,Buchberge算法会在有限步之内算出Gröbner基,具体参见 [10]。
定理2.1 设G为多项式理想I的Gröbner基,多项式
,则
当且仅当f被G除的余式为0,记为
。
定理2.1既可以作为Gröbner基的定义,也可以作为理想成员判定问题的解决方法。
3. 代数模型
我们验证具有2n个布尔输入
和个n布尔输出
的乘法器电路,电路的每个内部门(门输出)被一个门变量
表示。定义电路变量
我们将门输出(门变量) u与门的输入v,w用如下多项式(3.1)表示:
(3.1)
电路中的所有变量均为布尔变量。因此,我们可以得到关系式
,此关系式被称为域多项式F。每个门的输入与输出有相对应的变量,电路中的门被转换成这些变量的多项式关系,即通过多元多项式来模拟电路的运行方式 [11]。
4. Gröbner基方法及其优化
4.1. Gröbner基方法
定义4.1 设C是一个电路,
,G为电路C中每一个门对应的多项式(见(3.1))和输入变量的域多项式
及
构成的多项式集合。由G生成的理想记为
。
根据Gröbner基定义结合定义4.1.1可知按照字典项序
排列,G为
的Gröbner基。
定义4.2 设C是一个电路,多项式
,如果将
及由
表示的
的值代入到多项式p中结果为0,则称多项式p是电路C的规范多项式,记为PPC。电路C的所有PPC构成的集合定义为
。
定义4.3 若
是PPC,则电路C是乘法器电路。
推论4.1 任一多项式
,p是PPC当且仅当
。
根据以上定义我们可得:检验一个给定电路是否是乘法器可以归结为通过Gröbner基判定理想成员问题进行验证。即给定一个电路C和其对应的规范多项式p,检验p是否属于
。若p属于
,则该电路为乘法器电路,反之不成立。这一部分的理论知识也可以推广到任意非循环算术电路。
4.2. 逐位检测方法
逐位检测方法是使用列式项序将电路逻辑变成切片,应用Gröbner基方法验证每个电路切片的正确性进而验证乘法器的正确性。将乘法器验证问题分为更小更易于解决的子问题,逐步验证这些子问题进而验证乘法器。
如图1所示,在逐位检测方法中,每个电路切片包含且仅包含一个输出位。n位乘法器电路有2n个输出位,即有2n个电路切片。
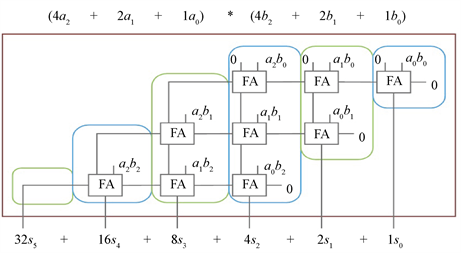
Figure 1. Schematic diagram of bit by bit detection method for 3-bit multiplier
图1. 3位乘法器的逐位检测方法示意图
定义4.4 设C是一个n位乘法器电路,有如下定义:
(1) 电路C的变量X上的一列多项式
是进位序列的进位多项式。
(2) 第i个电路切片部分乘积
。
(3) 第i个电路切片进位递归关系
。
通过这些定义,我们得到一个抽象定理,可以用来验证经过切片处理的乘法器。
定理4.1 设C是一个所有进位递归关系都成立的电路,若
,则C是乘法器。
证明
(4.1)
由定义4.3可知只要证明(4.1)是PPC即可证明电路C是乘法器。为了得到逐位检测算法,我们逐步定义切片。对每个切片中的输出
,定义它的输入锥即决定输出
的电路逻辑门(见图1)集合
。由输入锥可以定义切片
,
切片Gröbner基
为其切片
中所有门所对应的多项式集合。综上,即可得逐位检测算法:
在算法1中,
是由给定的第i列的部分乘积
、输出位
和进位多项式
唯一确定的,这就保证了进位递归关系
成立。实际上在算法中简单的取边界进位多项式
。从最后一个输出位
开始,求
模切片Gröbner基
和所有域多项式F的余式
,通过余式结果检测每个切片的正确性。若每个电路切片所得余式均为0,则电路C是乘法器电路,进而验证了乘法器的正确性。
5. Maple实现
Maple是一个具有强大符号计算能力的计算机代数系统,其符号计算能力是MathCAD和Matlab等软件符号处理的核心 [12]。
本文验证两种类型的乘法器,分别是btor乘法器和sp-ar-rc乘法器。在Gröbner基方法验证乘法器的Maple实现流程图中(见图2),file1.aig为乘法器通过AIGER [13] 转化得到的AIG文件。下面给出一个AIG文件的例子:
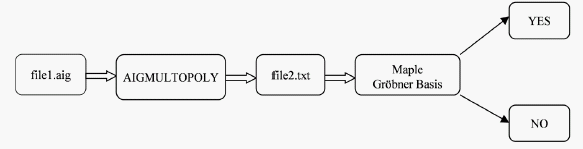
Figure 2. The Maple implementation flow chart of the multiplier verification based on Gröbner basis method
图2. Gröbner基方法验证乘法器的Maple实现流程图
aag 7 2 0 2 3 //标题
2 //输入a0
4 //输入a1
6 //输出b0
12 //输出b1
6 13 15 //与门0
12 2 4 //与门1
14 3 5 //与门2
AIG文件中第一行为标题行,7为最大变量索引,2为输入的个数,0为锁存的个数,2为输出的个数,3为与门的个数。依次列出乘法器的输入,输出和与门。本文所研究的乘法器不包含锁存,故L的值为0。我们重写验证工具AIGMULTOPOLY使其读取AIG文件后通过脚本文件中的命令行“Aigmultopoly $ aig_file $ Maple_script--maple”产生对应乘法器的Maple输出文件,通过脚本文件命令行“maple btori.maplet”使用Maple计算检测。AIGMULTOPOLY输出的 位乘法器Maple文件首先定义乘法器位数 和边界进位多项式
:
[>] with(Groebner);
[>] Size= n;
[>] Car(2*size)=0;
定义切片i的变量集M[i]和部分乘积集PP[i]。根据切片Gröbner基定义得
。
用切片i的规范多项式
归约Gröbner基
:
[>] Car[i]=NormalForm(s[i]+2Car(i+1)-PP[i],[op(FI),op(Fs[i-1]),
op(Fs[i]),op(CS[i-1]),op(CS[i]), op(Si)], plex(op(MS[i])));
归约通过Maple中Groebner基库的NormalForm函数 [14] 实现。NormalForm(f, polylist, order),其中f为被归约多项式,polylist为归约多项式集合,order为变量的序关系,我们使用的是字典序,对应Groebner基库中的plex函数。根据逐位检测算法知若电路所有切片归约得到的余式Car[i]的值均为0,则输入电路为乘法器电路,反之不成立。
我们使用Maple、Mathematica和Singular三种计算机代数系统分别对乘法器验证的Gröbner基方法和加法器重写(AR)优化的Gröbner基方法进行了实验。在我们的实验中,我们将挂钟时间设
置为1200秒,主内存限制为4 GB。所有实验中的时间都以秒为单位。我们从启动验证工具AIGMULTOPOLY开始计算到Maple、Mathematica和Singular完成计算为止,所包含的时间为AIGMULTOPOLY生成Maple、Mathematica和Singular文件的时间和使用相应计算机代数系统计算的时间。我们通过TO标记未完成的实验,MO标记达到内存限制、EE标记状态错误。实验结果如下表(见表1)所示:

Table 1. The implementation of Gröbner basis method based on different algebraic systems
表1. 基于不同代数系统的Gröbner基方法的实现
如表1所示,验证8~64位乘法器时,Maple计算速度较Mathematica相比更快且验证64位乘法器时,Maple不会出现Singular中超出内存限制的情况。验证128位乘法器时,环变量数超过32707个,Singular会出现错误 [15],使用Maple可以进行计算验证。但是由于C语言编程的多样性以及不同计算机代数系统不同版本的差异性使得Maple和Mathematica的验证时间略有差异。将来,我们将进一步重写优化验证工具以提高乘法器验证的效率。实验结果表明:Gröbner基方法验证乘法器通过Maple实现,在某种程度上加快了验证速度,为乘法器电路提供了强有力的验证平台。
6. 结束语
本文通过Maple实现乘法器验证的Gröbner基方法,为后续乘法器电路验证方法提供更多的计算机代数系统选择。随着验证方法的逐步优化,期望可以有更多的计算机代数系统可以加入到乘法器电路验证中,进一步提高验证的自动化程度。
NOTES
*通讯作者。