基于联合粒度属性约简信息损失的研究

Research on Information Loss of Attribute Reduction Based on Joint Granularity

摘要: 随着互联网技术的迅速发展，社会进入了大数据时代。数据不仅类型多种多样，结构错综复杂还具有动态变化的特点。如何从海量数据中快速获取有价值的信息是当前亟待解决的问题。粗糙集是一种处理数据不确定性的数据评价方法。属性约简是粗糙集理论的一个重要核心应用。本文将围绕属性约简后信息损失量进行研究，从而找寻一种属性约简算法，在约简后既能保持数据分类准确率较高且信息损失较少。本文借助知识粒度的概念和约简算法，引入联合粒度，并将其运用到属性约简过程，进一步得出基于联合粒度属性约简算法。然后运用其算法对决策表系统进行约简，得出该算法在保持分类准确率不变的情况下，其信息损失量降至较低。最后通过UCI数据集进行仿真实验探究，从而验证了该方法的准确性和有效性。

Abstract: With the rapid development of Internet technology, the society has entered the era of big data. The data is not only of various types and structures, but also of dynamic change. How to quickly obtain valuable information from massive data is an urgent problem to be solved. Rough set is a data evaluation method to deal with data uncertainty. Attribute reduction is an important core application of rough set theory. This paper will focus on the amount of information loss after attribute reduction, so as to find an attribute reduction algorithm, which can keep the data classification accuracy higher and information loss less after reduction. In this paper, the concept of knowledge granularity and reduction algorithm, the introduction of joint granularity, and its application to the process of attribute reduction, further get the attribute reduction algorithm based on joint granularity. Then the algorithm is used to reduce the decision table system. It is concluded that the information loss of the algorithm is reduced to a low level while the classification accuracy remains unchanged. Finally, the accuracy and effectiveness of this method are verified by the simulation experiment of UCI data set.

1. 引言

粗糙集理论 [1] 作为一种数据分析方法，在定性和定量分析的基础上用来描述决策系统中的不确定性。属性约简 [2] [3] [4] [5]，也称特征选择，是粗糙集理论的重要核心应用。它是从信息系统的所有属性中选择部分重要度较高的属性，同时不减少数据分类的准确性。属性约简已被广泛应用于许多研究领域，如模式识别、数据挖掘与机器学习等。在数据挖掘 [6] 领域中，属性约简是一种常用的数据处理工具，主要对数据中的冗余属性进行删除操作，使其达到更高的分类性能且不损失数据表的任何信息。

前期学者们提出了许多属性约简准则和约简算法，几乎所有的约简准则都宣称保持分类不变、信息无损失。然而，本文从信息熵角度 [6] 分析，定量分析删除的冗余属性可能含有一定的信息量，可以得出属性约简可能会导致信息的损失。为了探究不同约简准则信息损失量的差异，提出联合粒度属性约简算法，同时对比了正区域约简、知识粒度约简和该算法的约简准则对数据分类、信息损失量的影响，从而验证此算法的有效性。

2. 基础知识

给定一个信息系统 [1] $IS=\left(U,A\right)$ 中，U是论域，A是论域U上的条件属性集。在条件属性集中任取条件属性 $m\in A$ 都存在一个函数 $m:U\to F_m$，与其相对应， $F_m$ 为属性m的值域。U中每个元素称为个体、对象或行。

定义2.1 [5] 对于任意的属性子集 $B\subseteq A$ 和任何个体 $x\in A$ 都对应着如下的信息函数：

$In{f}_B\left(x\right)=\left\{\left(a,a\left(x\right)\right):a\in B\right\}$

B-不分明关系(或称为不可区分关系)定义为:

$IND\left(B\right)=\left\{\left(x,y\right):In{f}_B\left(x\right)=In{f}_B\left(y\right)\right\}$

任何满足 $IND\left(B\right)$ 的2个元素 $x,y$ 都不能由B的任何子集区分， ${\left[x\right]}_B$ 表示由x引导的 $IND\left(B\right)$ 等价类。

2.1. 属性约简

定义2.2 [6] 在决策系统 $DS=\left(U,C,d\right)$ 中， $B\subseteq C$ 是DS的基于正区域的相对约简当且仅当 $B\subseteq C$ 满足以下两个条件：

(1) $PO{S}_B\left(d\right)=PO{S}_C\left(d\right)$ ；

(2) 对于任意的 $a\in B$，都有 $PO{S}_{B-\left\{a\right\}}\left(d\right)\ne PO{S}_C\left(d\right)$.

定义2.3 [6] 给定一个决策系统 $DS=\left(U,A,d\right)$， $B\subseteq A$ 称为该决策系统DS的一个基于条件熵的相对约简当且仅当 $B\subseteq A$ 满足如下两个条件：

(1) $H\left(DS,\left\{d\right\}|B\right)=H\left(DS,\left\{d\right\}|A\right)$ ；

(2) 对任意的 $S\subset B$，均都有 $H\left(DS,\left\{d\right\}|S\right)\ne H\left(DS,\left\{d\right\}|A\right)$。

2.2. 知识粒度的基本概念

定义2.4 [7] 给定一个信息系统 $IS=\left(U,A,V,f\right)$，对于任意属性子集 $M\subseteq A$ 导出的划分 $U/M=\left\{R_1,R_2,R_3,\cdots ,R_n\right\}$，则该信息系统对于属性子集M的知识粒度的定义为

$GD\left(M\right)=\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\frac{|R_i{|}^2}{|U{|}^2}$

定义2.5 [7] 设给定一个信息系统 $IS=\left(U,A,V,f\right)$，如果存在属性子集 $R_1,R_2\subseteq A$，则有属性子集 $R_1$ 相对于子集 $R_2$ 的知识粒度的定义为

$GD\left(R_1|R_2\right)=GK\left(R_2\right)-GK\left(R_1\cup R_2\right)$

定义2.6 [7] 对于给定决策系统 $DS=\left(U,A\cup D,V,f\right)$，若属性子集 $R\subseteq A$ 是当且仅当满足以下两个条件：

(1) $GD\left(D|A\right)=GK\left(D|R\right)$ ；

(2) 对于任意的 $m\in R$， $GK\left(D|R-\left\{m\right\}\right)\ne GK\left(D|R\right)$。

称 $R\subseteq A$ 为该决策系统的一个知识属性约简。

定义2.7 [8] 在给定的信息系统 $IS=\left(U,A\cup D,V,f\right)$ 中，若存在属性子集 $c\in A$，则属性 $c\in A$ 与决策属性D的相似度定义为：

$s\left(c,D\right)=\frac{\left|IND\left(D\cup \left\{c\right\}\right)\right|}{\sqrt{\left|IND\left(c\right)\right|}\cdot \sqrt{\left|IND\left(D\right)\right|}}$

2.3. 知识粒度的启发式属性约简算法 [8]

根据知识属性约简的定义可得出一个属性约简算法，算法具体步骤如表1。

目前很多约简算法均要先求核属性，但该算法不需要。此算法在一定程度上减少了求核属性的工作量，同时时间复杂度相对缩减。

3. 联合粒度属性约简算法

受表1算法的启发，以知识粒度 [7] 作为启发式函数进行遍历搜索，选取知识粒度值的大小进行比较，得出一个新算法—基于联合粒度属性约简算法。算法的具体描述如表2所示。

Table 1. Heuristic attribute reduction algorithm based on knowledge granularity [8]

表1. 基于知识粒度的启发式属性约简算法 [8]

Table 2. Attribute Reduction Algorithm Based on Joint Granularity

表2. 基于联合粒度属性约简算法

基于联合粒度属性约简算法不同于上述表1，它主要从知识属性、粒计算 [9] 角度进行约简，可以直接对不同知识属性进行粒度和重要度的比较，同时使得约简过程更加精细，约简结果更加精确。

属性约简信息损失 [9]

定义3.1 [9] [10] [11] 在一个给定的决策系统 $DS=\left(U,A,d\right)$ 中，设A和 $\left\{d\right\}$ 在论域U上导出的划分分别为X和Y，其中 $X=U/A=\left\{X_1,X_2,\cdots ,X_N\right\}$， $Y=U/\left\{d\right\}=\left\{Y_1,Y_2,\cdots ,Y_M\right\}$， $p\left(X_i\right)=\frac{\left|X_i\right|}{\left|U\right|}$， $p\left(Y_j\right)=\frac{\left|Y_j\right|}{\left|U\right|}$， $p\left(X_i,Y_j\right)=\frac{\left|X_i\cap Y_j\right|}{\left|U\right|}$， $p\left(Y_j|X_i\right)=\frac{\left|X_i\cap Y_j\right|}{\left|X_i\right|}$， $i=1,2,\cdots ,N$， $j=1,2,\cdots ,M$. A和 $\left\{d\right\}$ 的信息熵 [12] 分别可

定义为：

$H\left(DS,A\right)=-{\displaystyle \underset{i=1}{\overset{N}{\sum }}p\left(X_i\right)lbp(\; X\; i\; )}$

$\left\{d\right\}$ 与A的联合熵 [13] 即可定义为：

$H\left(DS,A,\left\{d\right\}\right)=-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\displaystyle \underset{i=1}{\overset{M}{\sum }}p\left(X_i,Y_j\right)lbp\left(X_i,Y_j\right)}}$

定义3.2 [9] [10] [11] 给定 $DS=\left(U,A,d\right)$ 是一个决策系统， $B\subseteq A$ 是该决策系统的一个约简，则 $B\subseteq A$ 属性约简的信息损失定义如下：

$\Delta \left(B\right)=H\left(DS,A\right)-H\left(DS,B\right)$

$B\subseteq A$ 属性约简的信息损失率可定义如下：

$s\left(B\right)=\frac{\Delta \left(B\right)}{H\left(DS,A\right)}\times 100\%=1-\frac{H\left(DS,B\right)}{H\left(DS,A\right)}\times 100\%$

命题1 给定一个决策系统 $DS=\left(U,A,d\right)$，若 $B_1\subseteq A$ 是基于正区域的相对约简， $B_2\subseteq A$ 是基于知识粒度的属性约简， $B_3\subseteq A$ 是基于联合粒度的属性约简，则有 $\Delta \left(B_1\right)\ge \Delta \left(B_2\right)\ge \Delta \left(B_3\right)$.

证明：根据知识粒度约简、联合粒度约简及正区域相对约简可证。

例1下表所示 $D{S}_1=\left(U,C\cup D,V,f\right)$ 是一个决策表，如表3所示。U为论域，其中 $U=\left\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8\right\}$， $C=\left\{e_1,e_2,e_3,e_4\right\}$ 是条件属性， $D=\left\{d\right\}$ 是决策属性集。

Table 3. Decision System D S 1 = ( U , A , d )

表3. 决策系统 $D{S}_1=\left(U,A,d\right)$

$U/C=\left\{\left\{x_1\},\left\{x_2\right\},\{x_3,x_4\right\},\left\{x_5,x_6\right\},\left\{x_7\right\},\left\{x_8\right\}\right\}$

$U/\left\{d\right\}=\left\{\left\{x_1,x_3,x_5,x_7\right\},\left\{x_2,x_4,x_6,x_8\right\}\right\}$

由正区域的定义可得： $PO{S}_C\left(d\right)=\left\{x_1,x_2,x_7,x_8\right\}$。

根据条件属性依赖度的计算公式可得： ${\gamma }_C\left(D\right)\ne 1$，所以该决策表是不相容决策表。

(1) 根据知识粒度的属性约简算法可得约简后为： $R_1=RE{D}_C=\left\{e_2,e_3,e_4\right\}$.

根据属性约简的信息损失的计算方法可得：

$H\left(D{S}_1,C\right)=-{\displaystyle \sum p\left(X\right)lbp\left(X\right)}=2.5$

$H\left(D{S}_1,R_1\right)=-{\displaystyle \sum p\left(X\right)lbp\left(X\right)}=2.5$

故 $R_1$ 的信息损失量为： $\Delta \left(R_1\right)=0$。

(2) 由正区域约简算法可得： $R_2=\left\{e_2,e_3,e_4\right\}$， $R_3=\left\{e_1,e_3,e_4\right\}$

$H\left(D{S}_1,R_3\right)=-{\displaystyle \sum p\left(X\right)lbp\left(X\right)}=2$

故 $R_2$ 的信息损失量为0。

$R_3$ 的信息损失量为 $\Delta \left(R_3\right)=0.5$。

(3) 根据联合粒度属性约简算法可得： $R_4=\left\{e_2,e_3,e_4\right\}$

故 $R_4$ 的信息损失量为0。

例2下表所示为一个决策表， $D{S}_2=\left(U,A,d\right)$ 是一个决策系统，如表4所示。U为论域， $A=\left\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4\right\}$ 是条件属性， $\left\{d\right\}$ 是决策属性集。

Table 4. Decision system D S 2 = ( U , A , d )

表4. 决策系统 $D{S}_2=\left(U,A,d\right)$

$U/A=\left\{\left\{e_1\right\},\left\{e_2\right\},\left\{e_3\right\},\left\{e_4\right\},\left\{e_5\right\},\left\{e_6\right\}\right\}$， $U/\left\{d\right\}=\left\{\left\{e_1,e_4,e_6\right\},\left\{e_2,e_3,e_5\right\}\right\}$，

由正区域的定义可得： $PO{S}_A\left(d\right)=\left\{e_1,e_2,e_3,e_4,e_5,e_6\right\}$。

根据条件属性依赖度计算公式得： ${\gamma }_A\left(D\right)=1$，所以该决策表是相容决策表。

$H\left(D{S}_2,A\right)=-{\displaystyle \sum p\left(X\right)lbp\left(X\right)}=2.585$

(1) 基于正区域的相对约简： $S_1=\left\{a,b\right\}$

$H\left(D{S}_2,S_1\right)=-{\displaystyle \sum p\left(X\right)lbp\left(X\right)}=1.918$

故 $S_1$ 的信息损失量为： $\Delta \left(S_1\right)=0.667$。

(2) 基于知识粒度的属性约简： $S_2=RE{D}_A=\left\{a,b,e\right\}$

$H\left(D{S}_2,S_2\right)=-{\displaystyle \sum p\left(X\right)lbp\left(X\right)}=2.252$

故 $S_2$ 的信息损失量为： $\Delta \left(S_2\right)=0.333$。

(3)基于联合粒度的属性约简： $S_3=\left\{a,b,e\right\},S_4=\left\{a,b,c\right\}$

$H\left(D{S}_2,S_4\right)=-{\displaystyle \sum p\left(X\right)lbp\left(X\right)}=2.252$

故 $S_3,S_4$ 的信息损失量为： $\Delta \left(S_3\right)=\Delta \left(S_4\right)=0.333$。

4. 仿真实验分析

本节将采用一系列数据集进行验证本文所提出的算法的高效性和准确性。首先将本文提出的联合粒度属性约简算法与知识粒度属性约简算法、正区域相对约简算法 [14] 对同一组UCI数据集进行离散化处理，然后比较三种算法属性约简后的信息损失量从而验证本文算法的有效性。其实验平台的硬件环境为CPU Intel core i5和4 GB内存，操作系统为Windows 10专业版，实验所运用的编程工具为VC++6.0。

本次实验数据取自UCI数据集中的四组典型数据如表5所示。首先将每组数据集分成10等份，选择1份作为测试集，其他9份作为训练集，对这9份训练集进行联合粒度、知识粒度和正区域约简，然后比较它们约简后的信息损失量。

Table 5. Data set description

表5. 数据集描述

文中采用重庆邮电大学开发的RIDAS系统进行属性约简。使用正区域约简算法、知识粒度约简算法和联合粒度约简算法求取不同属性约简集合。根据信息熵的计算公式，根据已有计算信息熵的程序代码 [9]，计算给定信息系统的条件属性集合的信息熵及每个约简后的信息熵，可得出不同约简准则的信息损失量的大小以及信息熵与信息损失率之间的关系。

图1~4分别表示四组数据集的约简准则与信息损失量仿真实验结果图，其中横坐标表示属性约简结果，纵坐标表示信息损失量大小。图5~8分别表示四组数据集约简后集合的信息熵与信息损失率仿真实验图，其中横坐标表示约简后信息熵，纵坐标表示信息损失率大小。

根据上述8张图示可以清楚地看出，本文提出的基于联合粒度属性约简的信息损失远小于基于正区域、基于知识粒度属性约简信息损失，从而说明本文提出的基于联合粒度属性约简算法的有效性，可以有效地解决大数据时代下海量数据的约简，减少约简导致的分类准确率较低、信息损失量较大的问题。

Figure 1. Comparison of dermatology

图1. Dermatology比较

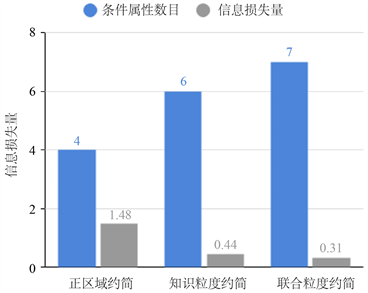
Figure 2. Comparison of conceptual method choices

图2. Contraceptive Method Choice比较

Figure 3. Comparison of mushroom

图3. Mushroom比较

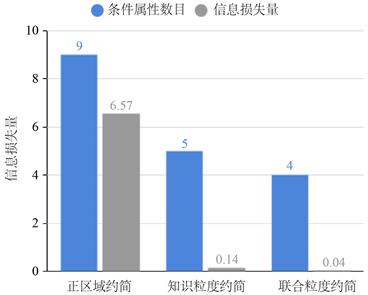
Figure 4. Comparison of letter recognition

图4. Letter Recognition比较

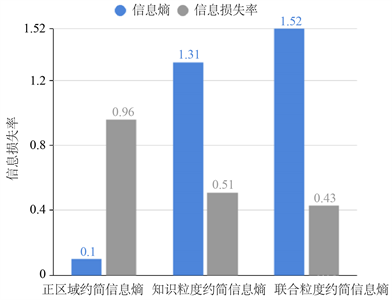
Figure 5. Analysis of dermatology

图5. Dermatology分析

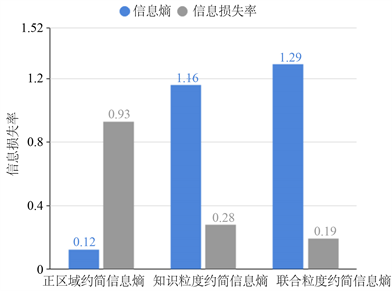
Figure 6. Analysis of conceptual method choice

图6. Contraceptive Method Choice分析

Figure 7. Analysis of mushroom

图7. Mushroom分析

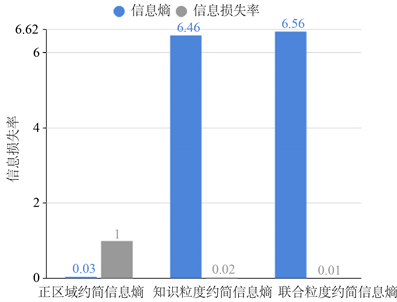
Figure 8. Analysis of letter recognition

图8. Letter Recognition分析

5. 结论

本文通过引入联合粒度的概念，并将其运用到粗糙集理论的属性约简 [15] 中，提出了基于联合粒度属性约简算法，然后分析比较不同的属性约简产生的信息损失，最终得到本文的基于联合粒度的属性约简不仅能保持数据分类的准确性，同时也能维持约简后的信息损失较低的结论。后续我们将继续研究该算法对带权决策表的约简信息损失的影响及进一步的优化。