1. 引言
睡眠是一种自发的、主动的调节过程,睡眠质量对人的身心状态有着重大影响。然而,随着生活节奏的加快,生存压力不断增大,人类的睡眠质量开始出现问题,这使人们在身体上、心理上饱受折磨,也严重影响人类的生活质量。因此,如何提高睡眠质量,减少睡眠相关疾病对健康的影响,受到了广泛的关注。
临床医学上不同时间的睡眠深度是睡眠质量判定的一个主要方面 [1],对人体睡眠的分期研究能够帮助对不同时间的睡眠深度进行准确的评估,是监测和研究人类睡眠质量和相关疾病的关键。人体在进入睡眠时大脑将以一种电信号(Electroence phalogram, EEG)形式在作用,脑电信号在不同睡眠分期所呈现的特点有所不同 [2]。基于脑电信号进行自动分期,是评估睡眠质量、诊断和治疗睡眠相关疾病的重要辅助工具,相应的研究对于预防和治疗相关的疾病有着十分重要的临床意义与应用价值。
对于利用脑电信号对睡眠状态进行分期的研究,已有诸多研究成果。2007年李谷等 [3] 在基于脑电信号Hilbert-Huang变换的睡眠分期研究中对560个睡眠脑电信号样本进行分期。2010年刘慧等 [4] 在基于模糊熵的脑电睡眠分期特征提取与分类的研究中,对数据进行模糊熵的分析,并且利用支持向量机对睡眠状态进行分类。2012年Liang等 [5] 使用多尺度熵和线性判别分析法来分析睡眠EEG信号并对其分期。2013年周鹏等 [6] 使用主成分分析法处理脑电信号,并利用SVM实现睡眠分期。2015年,Diykh M等 [7] 对睡眠分期研究中,利用结构图相似和K-means的方法对提取的EEG信号的时频统计特征量进行分析,但是这个方法实时性不好并且实用价值不大。2016年,张晓宇等 [8] 利用快速傅里叶变换处理脑电信号,并对频谱结果做符号化,将符号化之后的结果作为BP神经网络的输入参数实现睡眠自动分期。以上研究在睡眠状态分期预测中均取得较理想的效果,但在预测模型构建当中需要耗费大量时间,依然有很大的改进空间。
为了解决耗时过长的问题,本文在支持向量机分类应用于睡眠分期预测模型构建的研究基础上,采用K边界近邻法支持向量预选取算法 [9] 来构建支持向量候选集,将支持向量候选集输入到SVM中训练,减少训练样本,在保证良好分类预测准确度的前提下加快训练速度,大量减少睡眠分期预测模型构建的时间。
本文第2节介绍支持向量机和K边界近邻法支持向量预选取算法,第3节构建睡眠分期预测模型,第4节是睡眠分期预测模型数值实验。
2. 支持向量机和K边界近邻法支持向量预选取算法
2.1. 支持向量机简介
支持向量机是在统计学习的背景下产生的一种机器学习方法,由Vapnik [10] 和Cortest提出,是一种结构风险最小化的理论,主要用来解决非线性回归和分类问题。
假设训练样本
,
表示输入模式的特征空间。SVM中训练的目的是在泛化误差达到最小(或有上界)的前提下,找到最优判决函数
,将两类数据分开。假定具有最大分类间隔的超平面为
,该超平面可以满足上述条件,它是由法向量
和截距b决定。为了找到该分离超平面,我们需要求解以下凸二次规划问题 [11]:
(1)
其中
是惩罚因子,
是拉格朗日乘子,
是核函数。
通过对式(1)求解可得
。法向量
,选择
的一个正分量
,可求得截距
。引入核函数
,由凸二次规划问题得到最优判
决函数为:
。 (2)
其中
是一个符号函数,
对应的样本被称为支持向量。
SVM是二分类模型分类器,但也可以做多分类。目前建立SVM多分类器的方法有很多,常见的是利用多个二分类器组合构造一个多分类器,可以用于多分类数据的处理 [12]。已有诸多学者将SVM分类器应用于睡眠状态的识别,为了保证识别的准确度,睡眠分期预测模型的建立需要大量睡眠脑电信号样本参与SVM训练,这将导致训练时间过长。
2.2. K边界近邻法支持向量预选取算法
K边界近邻法是一种支持向量机预选取方法,SVM的最优分离超平面由支持向量来确定,而支持向量只占全部训练集的一小部分 [9]。因此,通过选取距离每个样本最近的k个异类样本作为支持向量机候选集,并将其作为训练样本进行SVM训练,能够在不影响支持向量机分类性能的前提下,大大减少训练样本,提高训练速度 [13]。
已知训练样本分为两类,正类样本
和负类样本
,
,
,
其中
,
,
,M是样本维度。
已知有两类样本
,当它们线性可分时,它们之间的样本距离可以用欧氏距离来表示:
, (3)
当两类样本非线性可分时,通过映射函数
将原输入空间映射到高维的特征空间中,样本在高维的特征空间中变得线性可分,这时的样本距离被称为非线性距离:
, (4)
其中
是核函数。常用的核函数有线性核,多项式核、高斯核以及S型核。其中,高斯核函数因对于高维样本数据的分类问题也能有很好的识别效果而被频繁使用。高斯核函数如下:
, (5)
其中r是一个常数。
在某一类中,位于该类边界上的向量称为边界向量。已知有正类样本集
和负类样本集
,
为
中的第i个样本与
中的第j个样本之间的距离。对于
中的每一个
,将
与
距离最小的k个样本定义为
的边界向量;同理,可以定义
的边界向量。当i和j遍历所有值后就可以得到边界向量集。
KNBN方法的具体步骤:
(1) 从正类样本集
中选择一个样本
,求
与所有负类样本之间的距离,保留最近的k个负类样本,将它们放入边界向量集当中。
(2) 返回步骤(1),直至遍历所有正类样本为止。
(3) 将所有负类样本按照步骤(1)和步骤(2)操作,保留离每个负类样本最近的k个正类样本,将它们放入边界向量集当中。
(4) 把上面得到的边界向量集当中相同的支持向量删去,进行唯一化处理,最终得到支持向量候选集。
如图1所示,选取的样本都是离选定样本最近的另类样本,所以KNBN选出的向量一定为与两类样本的分布无关。因此,选取适当的k值,边界向量集一定能包含所有的支持向量,构造出一个支持向量候选集。

Figure 1. Diagram of KNBN support vector preselection
图1. KNBN支持向量预选取示意图
3. 睡眠分期预测模型
3.1. 睡眠分期基础理论
睡眠过程是动态并且复杂的。在国际睡眠分期的判读标准R & K [14] 中,将睡眠状态分为:清醒期,快速眼动期(REM)和非快速眼动期(NREM);在非快速眼动期中,根据睡眠状态由浅入深的逐步变化,又进一步分为睡眠I期,睡眠II期,睡眠III期和睡眠IV期;其中睡眠III期和睡眠IV期又可合并为深睡眠期。睡眠分期如图2所示。
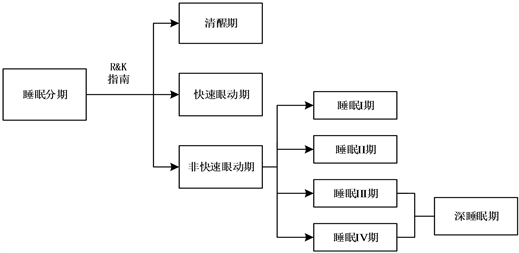
Figure 2. Diagram of sleep stages classification
图2. 睡眠分期示意图
大脑的活动状态在各个睡眠时期具有显著差异,睡眠脑电信号是一种自发型的脑电信号,其中包含了睡眠时期大量的大脑信息。引言部分已经提到基于脑电信号对睡眠分期进行分析研究,是诊断和治疗睡眠疾病的重要辅助工具。而脑电信号作为一种生理信号,其具有随机性强,信号微弱,一般波幅范围在0~200 μv,并且该信号极易受到噪声干扰。同时频率较低,频域特征比较突出,其范围一般为0.5~100 Hz。此外,EEG信号是一种典型的非线性信号,表现出较强的非平稳性 [15]。
在睡眠过程中,主要经历了快速眼动期和非快速眼动期两个大时期,EEG信号在不同睡眠分期所呈现的特点有所不同。如图3所示,自上而下依次为清醒期、睡眠I期、睡眠II期、深睡眠和快速眼动期的脑电信号时序列。
由于在不同睡眠期EEG信号有不同特征,因此我们可以利用其各个睡眠期EEG信号的特点,进行SVM分类。基于脑电信号的SVM睡眠分期模型,能够帮助更好的识别睡眠状态,有利于对相关睡眠疾病的防预和治疗。
3.2. 基于标准SVM的睡眠分期预测模型
机器学习中分类方法众多,SVM是近年来使用较多的一种方法,尤其是SVM具有判别能力优良、泛化能力强、参数设置简单等优点。本文利用SVM的诸多优点与脑电信号时序列的特点,将SVM分类方法用于脑电信号数据的分类处理,进而以较高准确率识别睡眠状态。
本文基于标准SVM算法构建睡眠分期预测模型,下面是分期预测模型的步骤:
(1) 对EEG信号样本数据进行归一化处理;
(2) 归一化后的数据分成训练数据集和测试数据集;
(3) 将EEG信号样本中的训练数据集输入至SVM分类器当中,构建基于标准SVM的睡眠分期预测模型;
(4) 测试数据集代入步骤(3)中的睡眠分期预测模型进行预测,得到预测结果。
3.3. 基于KNBN-SVM的睡眠分期预测模型
基于标准SVM的睡眠分期预测模型能达到较为理想的预测效果,但在实验测试所采集到的EEG信号样本中,包含了一些无用的或是冗余样本。换言之,训练样本中包含了支持向量和非支持向量,因此SVM的训练中还包括了对非支持向量的优化,需要花费大量的训练时间。
本文使用K边界近邻法支持向量预选取方法(KNBN)对EEG信号训练样本进行支持向量预选取。通过KNBN方法可以减少EEG信号训练样本中的冗杂样本和对分类无用的多余样本,再用SVM来训练和预测,从而减少预测模型建立的训练时间并在一定程度上提高分类预测准确度。
下面为基于KNBN-SVM的睡眠分期预测算法步骤:
(1) 将EEG信号样本数据进行归一化处理,并分成训练样本和测试样本;
(2) 将训练数据集按睡眠分期标签分为五类,随机选取其中的某一类作为正类,其余四类作为负类,按照2.2中KNBN方法在两类数据集中预选取出边界向量;
(3) 当五类样本中的每一类样本都经历过作为正样本之后,得到一个原始训练数据集的边界向量集,将其中相同的样本唯一化处理,得到支持向量候选集;
(4) 将步骤(3)中得到的支持向量候选集作为训练数据集输入到SVM模型中,得到一个五分类的睡眠分期预测模型;
(5) 将测试数据集输入到步骤(4)中得到的睡眠分期预测模型中得到分类准确度及训练时长。
图4是基于KNBN-SVM的睡眠分期预测模型流程图:
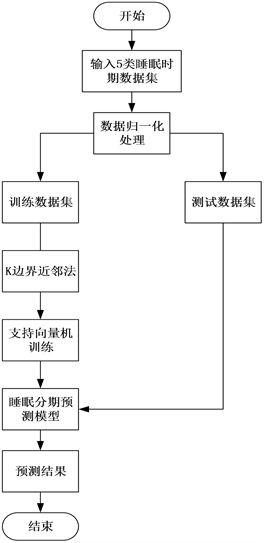
Figure 4. Flow chart of sleep staging prediction model based on KNBN-SVM
图4. 基于KNBN-SVM的睡眠分期预测模型流程图
4. 睡眠分期预测模型数值实验
下面为了讨论KNBN-SVM算法对于睡眠分期预测的有效性和可行性,将KNBN-SVM算法和标准的SVM算法下构建的睡眠分期预测模型的实验结果进行分析和比较。本文是在Matlab R2018a环境中,2.3 GHz,Pentium,DualCPU,4 GB内存的硬件平台上进行。
本文睡眠分期预测实验数据采用“‘华为杯’第十七届中国研究生数学建模竞赛”赛题C题的睡眠脑电信号数据。该数据中共包含五类睡眠状态数据集,分别为:清醒期、快速眼动期、睡眠I期、睡眠II期和深睡眠期,共有3633个样本,随机选取3600个EEG信号样本参与实验,其中2000个样本为训练样本,1600个样本为测试样本。按照3.2中的流程构建基于标准SVM的睡眠分期预测模型,并代入EEG信号测试数据集得到基于标准SVM的睡眠分期预测模型的预测准确度以及训练耗时。对于KNBN-SVM方法,将实验数据集按照3.3中的流程,先使用KNBN方法在原始的EEG训练样本集中预选取支持向量,再将支持向量候选集作为新的训练样本代入SVM中训练,构建基于KNBN-SVM的睡眠分期预测模型,最后代入EEG信号测试样本得到KNBN-SVM训练算法的预测准确度和训练总耗时,其中KNBN-SVM算法的训练时长为预选取边界向量集的时间和SVM训练时间的总和,KNBN的参数值 [9]
。SVM和KNBN-SVM中数据训练采用的核函数均选为高斯核函数,其中
。实验结果如表1所示,实验结果为100次独立实验结果的平均值。
从表1中可以看出,直接使用标准的SVM训练2000个训练样本,得到的分类预测准确率为73.75%,训练耗时864 ms;KNBN-SVM方法中对训练数据进行KNBN支持向量预选取选取出1205个边界向量作为支持向量候选集。将支持向量候选集作为训练样本集输入到标准SVM当中训练,得到的分类预测准确率为75.31%,训练总耗时380 ms。实验结果表明,KNBN-SVM训练算法的训练样本比标准的SVM算法的训练样本减少了39.75%,训练总耗时减少了484 ms,预测准确度提升了1.56%。

Table 1. Comparison of sleep stages classification of SVM and KNBN-SVM
表1. 标准SVM和KNBN-SVM的睡眠分期预测模型比较
5. 结语
本文将支持向量机分类应用于睡眠分期预测模型的研究,使用脑电信号时序列作为睡眠状态识别的工具,构建基于标准SVM的睡眠分期预测模型和基于KNBN-SVM的睡眠分期预测模型,并进行比较。实验表明,基于标准的SVM的睡眠分期预测模型预测准确度较理想;基于KNBN-SVM的睡眠分期预测模型不仅相对于标准的SVM准确度有所提高,而且还大幅度的缩短了训练时间。因此,KNBN-SVM方法适用于睡眠分期的研究,对于预防和治疗相关的疾病有着一定的应用价值。
NOTES
*第一作者。