基于晶格动力学的硅单晶热学性质研究(I)——晶格动力学与比热

Study on Thermal Properties of Silicon Single Crystal Based on Lattice Dynamics (I)—Lattice Dynamics and Specific Heat

摘要: 为探究硅单晶在低温下的热学性质，本文提出了用晶格动力学进行硅单晶热学性质计算的思路，并运用他人计算得到的最近邻和次近邻原子间个数有限的相互作用力常数，推导了完整的晶格动力学力常数矩阵和晶格动力学矩阵，并求解晶格动力学矩阵的本征值问题，得到了比热与温度的关系的数值计算结果。结果表明，本文计算得到的比热与他人通过实验得到的数据吻合，因此我们推导得到的晶格动力学矩阵是正确的，从而也能用于硅单晶的其它热学性质的计算。

Abstract: In order to study the thermal properties of silicon single crystal at low temperature, this paper puts forward the idea of calculating the thermal properties of silicon single crystal by lattice dynamics. The complete lattice dynamic force constant matrix and lattice dynamic matrix are derived by using the finite number of interaction forces between the nearest neighbor atoms and the next-nearest neighbor atoms calculated by others; then the eigenvalue problem of lattice dynamics matrix is solved; and the relationship between specific heat and temperature is calculated. It is found that the specific heat calculated by us coincides with those experimental results obtained by others, so the lattice dynamic matrix derived by us is correct, and can be used to calculate the other thermal properties of silicon single crystal.

1. 引言

利用具有负热膨胀性质的材料，就可以制备具有任意膨胀系数的复合材料，来调节材料的膨胀系数，甚至实现零膨胀，从而实现对材料热膨胀性质的裁剪和调控，满足众多领域对各种具有特定热膨胀性质的材料的需求。因此负热膨胀材料具有广泛的应用前景 [1]。硅单晶是非常重要的半导体材料，在集成电路和MEMS中一直扮演着重要角色，并在低温下有负热膨胀性质。对硅单晶的热膨胀性质的研究，将有助于对基于热膨胀性质的MEMS热驱动部件正确地进行设计，也有助于对装配或使用过程中所产生热应力进行预测而防止这些热应力对集成电路和MEMS的破坏。然而到目前为止，人们对硅单晶的负热膨胀性质的物理机制还不甚明了。

在对热膨胀性质进行理论研究的早期，人们用了过于简单的单原子或双原子的简单振子模型，因而很难保证研究结果的准确性 [2]。近年来人们广泛采用经典分子动力学研究热膨胀性质，由于该理论方法是建立在经典牛顿力学基础上的，忽视了量子效应，因而对低温下的热膨胀性质的计算也不正确 [3]。目前也有人采用从头计算方法计算力常数，再用准简谐近似(QHA)来研究固体材料的热膨胀性质 [4] [5]。由于QHA方法没有为热膨胀和非线性力常数之间提供简单明了的关系，人们不可能借助于QHA方法对硅单晶体在低温下的负热膨胀性质的物理机制做出合理的解释。

热膨胀源于原子间的非线性力常数和非和谐势能。我们曾提出了一种观点 [6]，认为硅晶体中的最近邻原子间存在的两体势中的非和谐势能随键长的增加而减小，所以在全温度范围对键长提供了正热膨胀的贡献，并且随温度从0 K增加，这部分热膨胀系数也从零开始增加；硅晶体中的一个原子和两个与之最近邻原子间存在三体势，该三体势中的和谐势能随键长的增加而增加，所以在全温度范围提供了负热膨胀的贡献，并且随着温度从0 K增加，这部分热膨胀系数也从零开始减小(负得更多)；在低温下，由于三体势引起的负热膨胀系数绝对值超过了两体势引起的正热膨胀系数，所以硅单晶总体呈现负热膨胀；而随温度的进一步升高，由于两体势引起的正热膨胀系数超过了三体势引起的负热膨胀系数绝对值，所以硅单晶总体呈现正热膨胀。但当时由于缺少来自于硅单晶中原子间相互作用力常数的直接数据支持，因此我们对硅单晶负热膨胀机制的解释还只能归于是一种假设。

由于在晶格动力学中，将晶格振动的能量量子化为了符合玻色统计的声子，即考虑了量子效应，所以用晶格动力学进行热膨胀性质的计算，结果肯定比分子动力学准确 [7] [8]。另外，由于在晶格动力学中，晶格原子位移等都有解析表达式，因此借助于量子力学微扰论，可以得到热膨胀系数的解析公式，使数值计算的工作量远远低于分子动力学的计算工作量，我们还可以从解析公式入手，分析硅单晶低温负热膨胀的机制。除此之外，晶格动力学也可以用于硅单晶的比热、热传导等热学性质研究。由于晶格动力学是建立在对晶格动力学矩阵本征值问题的求解基础上的，因此本文将运用Rignanese等人计算得到的最近邻和次近邻原子间个数有限的相互作用力常数 [5]，推导、计算完整的晶格动力学力常数矩阵，并在此基础上推导和计算晶格动力学矩阵，再求解晶格动力学矩阵的本征值问题，得到了比热与温度的关系的数值计算结果，并将之与他人通过实验得到的数据进行比较，从而对我们推导得到的晶格动力学矩阵的正确性进行评价，为后续硅单晶热膨胀等其它的热学性质的计算做必要准备。

2. 硅晶体结构及原子间线性力常数矩阵

硅单晶体具有金刚石结构，原子质量为m，每个原胞中有两个互为最近邻的硅原子，处于位置 $\left(l_x,l_y,l_z\right)a/2$ 的原子A被称为1类原子，而处于位置 $\left(l_x+1/2,l_y+1/2,l_z+1/2\right)a/2$ 的原子B被称为2类原子，其中， $l_x$、 $l_y$ 和 $l_z$ 为整数，a为晶格常数。根据硅单晶体的结构，可得原子O的其它三个最近邻原子B、C和D的位置分别为 $\left(l_x,l_y+1,l_z+1\right)a/2$、 $\left(l_x+1,l_y+1,l_z\right)a/2$ 和 $\left(l_x+1,l_y,l_z+1\right)a/2$；原子A的其它三个最近邻原子b、c和d的位置为 $\left(l_x+1/2,l_y-1/2,l_z-1/2\right)a/2$、 $\left(l_x-1/2,l_y-1/2,l_z+1/2\right)a/2$ 和 $\left(l_x-1/2,l_y+1/2,l_z-1/2\right)a/2$。

晶体中原子围绕平衡位置进行热运动，设原胞l中原子 $\chi$ 在 $\sigma$ 方向上的瞬时振动位移为 $u_{l\chi }^{\sigma }$，在线性近似下，与晶格振动有关的晶体的原子间相互作用势能可展开为：

$\text{U}=\frac{1}{2}\underset{l\chi \sigma }{{\displaystyle \sum }}\underset{l^{\prime }{\chi }^{\prime }{\sigma }^{\prime }}{{\displaystyle \sum }}\frac{{\partial }^2\text{U}}{\partial u_{l\chi }^{\sigma }\partial u_{l^{\prime }{\chi }^{\prime }}^{{\sigma }^{\prime }}}{u}_{l\chi }^{\sigma }{u}_{l^{\prime }{\chi }^{\prime }}^{{\sigma }^{\prime }}$ (1)

其中 $\chi$ 为1或2，分别代表每个原胞中的两个原子，例如，原子A和O组成一个原胞，A为1类原子，O为2类原子。 $l=\left(l_x,l_y,l_z\right)$ 代表不同的原胞， 为x、y或z， $u_{l\chi }^{\sigma }$ 代表l原胞中原子 $\chi$ 在 $\sigma$ 方向上的振动位移， ${\partial }^2\text{U}/\partial u_{l\chi }^{\sigma }\partial u_{l^{\prime }{\chi }^{\prime }}^{{\sigma }^{\prime }}$ 被称为线性力常数， $l\chi$ 和 $l^{\prime }{\chi }^{\prime }$ 原子间的9个力常数，构成一个线性力常数矩阵

${\Phi }_{l\chi l^{\prime }{\chi }^{\prime }}=\left(\begin{array}{ccc}\frac{{\partial }^2\text{U}}{\partial u_{l\chi }^x\partial u_{l^{\prime }{\chi }^{\prime }}^x}& \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^x\partial u_{l^{\prime }{\chi }^{\prime }}^y}& \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^x\partial u_{l^{\prime }{\chi }^{\prime }}^z}\\ \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^y\partial u_{l^{\prime }{\chi }^{\prime }}^x}& \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^y\partial u_{l^{\prime }{\chi }^{\prime }}^y}& \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^y\partial u_{l^{\prime }{\chi }^{\prime }}^z}\\ \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^z\partial u_{l^{\prime }{\chi }^{\prime }}^x}& \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^z\partial u_{l^{\prime }{\chi }^{\prime }}^y}& \frac{{\partial }^2\text{U}}{\partial u_{l\chi }^z\partial u_{l^{\prime }{\chi }^{\prime }}^z}\end{array}\right)$ (2)

由上式可知， ${\Phi }_{l\chi l^{\prime }{\chi }^{\prime }}$ 和 ${\Phi }_{l^{\prime }{\chi }^{\prime }l\chi }$ 互为转置矩阵，因此两者只需求其一。

同一原胞中的原子A、O是最近邻原子，它们之间的线性力常数 ${\partial }^2\text{U}/\partial u_{lA}^{\sigma }\partial u_{lO}^{{\sigma }^{\prime }}$ 可构成一个矩阵，采用Herman符号系统 [9]，可表示为

${\Phi }_{OA}=\left(\begin{array}{ccc}\alpha & \beta & \beta \\ \beta & \alpha & \beta \\ \beta & \beta & \alpha \end{array}\right)$ (3)

根据硅单晶结构的对称性，可以直接给出原子O与最近邻原子B、C和D，以及原子A与最近邻原子b、c和d之间的线性力常数矩阵

${\Phi }_{OB}={\Phi }_{Ab}=\left(\begin{array}{ccc}\alpha & \bar{\beta }& \bar{\beta }\\ \bar{\beta }& \alpha & \beta \\ \bar{\beta }& \beta & \alpha \end{array}\right)$ (4)

${\Phi }_{OC}={\Phi }_{Ac}=\left(\begin{array}{ccc}\alpha & \beta & \bar{\beta }\\ \beta & \alpha & \bar{\beta }\\ \bar{\beta }& \bar{\beta }& \alpha \end{array}\right)$ (5)

${\Phi }_{OD}={\Phi }_{Ad}=\left(\begin{array}{ccc}\alpha & \bar{\beta }& \beta \\ \bar{\beta }& \alpha & \bar{\beta }\\ \beta & \bar{\beta }& \alpha \end{array}\right)$ (6)

原子A与B互为次近邻原子，采用Herman符号系统，它们之间的线性力常数矩阵可表示为：

${\Phi }_{AB}=\left(\begin{array}{ccc}\lambda & \bar{\delta }& \bar{\delta }\\ \delta & \mu & \nu \\ \delta & \nu & \mu \end{array}\right)$ (7)

根据晶体的对称性，将晶格分别绕x轴转动180˚，可得与原子B、C和D相对应的原子 $B^{\prime }$、 $C^{\prime }$ 和 $D^{\prime }$，然后沿y轴转动180˚，由原子B、C、D、 $B^{\prime }$、 $C^{\prime }$ 和 $D^{\prime }$ 分别得原子 $B^{″}$、 $C^{″}$、 $D^{″}$、 $B^{‴}$、 $C^{‴}$ 和 $D^{‴}$，它们构成了除原子B、C和D外的原子A的另外9个次近邻原子。原子 $B^{\prime }$、 $C^{\prime }$ 和 $D^{\prime }$ 的位置分别为： $\left(l_x,l_y-1,l_z-1\right)a/2$、 $\left(l_x+1,l_y-1,l_z\right)a/2$ 和 $\left(l_x+1,l_y,l_z-1\right)a/2$，原子 $B^{″}$、 $C^{″}$ 和 $D^{″}$ 的位置分别为： $\left(l_x,l_y+1,l_z-1\right)a/2$、 $\left(l_x-1,l_y+1,l_z\right)a/2$ 和 $\left(l_x-1,l_y,l_z-1\right)a/2$，原子 $B^{‴}$、 $C^{‴}$ 和 $D^{‴}$ 的位置分别为： $\left(l_x,l_y-1,l_z+1\right)a/2$、 $\left(l_x-1,l_y-1,l_z\right)a/2$ 和 $\left(l_x-1,l_y,l_z+1\right)a/2$。根据硅晶体结构的对称性，可得以下原子A和所有次近邻原子间的线性力常数矩阵

${\Phi }_{AB}={\Phi }_{B^{\prime }A}={\Phi }_{Ob}={\Phi }_{b^{\text{'}}O}=\left(\begin{array}{ccc}\lambda & \bar{\delta }& \bar{\delta }\\ \delta & \mu & \nu \\ \delta & \nu & \mu \end{array}\right)$ (8)

${\Phi }_{A{B}^{″}}={\Phi }_{B^{‴}A}={\Phi }_{O{b}^{″}}={\Phi }_{b^{‴}O}=\left(\begin{array}{ccc}\lambda & \delta & \bar{\delta }\\ \bar{\delta }& \mu & \bar{\nu }\\ \delta & \bar{\nu }& \mu \end{array}\right)$ (9)

${\Phi }_{AC}={\Phi }_{C^{\prime }A}={\Phi }_{Oc}={\Phi }_{c^{\prime }O}=\left(\begin{array}{ccc}\mu & \nu & \delta \\ \nu & \mu & \delta \\ \bar{\delta }& \bar{\delta }& \lambda \end{array}\right)$ (10)

${\Phi }_{A{C}^{″}}={\Phi }_{C^{‴}A}={\Phi }_{O{c}^{″}}={\Phi }_{c^{‴}O}=\left(\begin{array}{ccc}\mu & \bar{\nu }& \delta \\ \bar{\nu }& \mu & \bar{\delta }\\ \bar{\delta }& \delta & \lambda \end{array}\right)$ (11)

${\Phi }_{AD}={\Phi }_{D^{\prime }A}={\Phi }_{Od}={\Phi }_{d^{\prime }O}=\left(\begin{array}{ccc}\mu & \delta & \nu \\ \bar{\delta }& \lambda & \bar{\delta }\\ \nu & \delta & \mu \end{array}\right)$ (12)

${\Phi }_{A{D}^{″}}={\Phi }_{D^{‴}A}={\Phi }_{O{d}^{″}}={\Phi }_{d^{‴}O}=\left(\begin{array}{ccc}\mu & \bar{\delta }& \nu \\ \delta & \lambda & \delta \\ \nu & \bar{\delta }& \mu \end{array}\right)$ (13)

设晶体中每个原子都作相同位移 $u_{\beta }$，则晶体中任一原子 $l\chi$ 受力 $F_{\alpha }\left(l\chi \right)$ 为零，即

${\displaystyle \underset{\beta }{\sum }{\displaystyle \underset{l^{\prime }{\chi }^{\prime }}{\sum }{\Phi }_{\alpha \beta }\left(l\chi ,l^{\prime }{\chi }^{\prime }\right)u_{\beta }}}=0$ (14)

由于上式中 $u_{\beta }$ 可取任意值，可得

$\Phi \left(l\chi ,l\chi \right)=-\underset{l^{\prime }{\chi }^{\prime }\ne l\chi }{{\displaystyle \sum }}\Phi \left(l\chi ,l^{\prime }{\chi }^{\prime }\right)$ (15)

根据(15)式和式(3)~(13)，可得

$\Phi \left(l\chi ,l\chi \right)=-\left(4\alpha +4\lambda +8\mu \right)\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$ (16)

Rignanese等人 [5] 由第一性原理出发计算得到了硅晶体原子间相互作用线性力常数，结果表明，超出次近邻原子之外的原子间相互作用线性力常数与近邻和次近邻原子间的线性力常数相比可以忽略。因此只考虑近邻和次近邻原子间的相互作用，根据以上各式即可确定所有线性力常数矩阵。

3. 晶格动力学矩阵

根据(1)式，可得原子 $l\chi$ 在 $\alpha$ 方向所受作用力公式

$F_{\alpha }\left(l\chi ,t\right)=-\underset{l^{\prime }{\chi }^{\prime }{\alpha }^{\prime }}{{\displaystyle \sum }}{\Phi }_{\alpha {\alpha }^{\prime }}\left(l\chi ,l^{\prime }{\chi }^{\prime }\right)u_{{\alpha }^{\prime }}\left(l^{\prime }{\chi }^{\prime },t\right)$ (17)

根据牛顿第二定律，得晶格原子运动方程。

$m{\ddot{u}}_{\alpha }\left(l\chi ,t\right)=-\underset{l^{\prime }{\chi }^{\prime }{\alpha }^{\prime }}{{\displaystyle \sum }}{\Phi }_{\alpha {\alpha }^{\prime }}\left(l\chi ,l^{\prime }{\chi }^{\prime }\right)u_{{\alpha }^{\prime }}\left(l^{\prime }{\chi }^{\prime },t\right)$ (18)

由于在大块晶体中存在行波，因而可以将(18)式的解设为

$u_{\alpha }\left(l\chi ,t\right)=\frac{e_{\alpha }\left(\chi \right)}{\sqrt{m}}{\text{e}}^{i\left[k\cdot R\left(l\right)-\omega t\right]}$ (19)

其中， $\omega$ 为频率， $k$ 为格波波矢。将(19)式代入(18)式，得

${\omega }^2{e}_{\alpha }\left(\chi \right)=\underset{{\chi }^{\prime }{\alpha }^{\prime }}{{\displaystyle \sum }}{D}_{\alpha {\alpha }^{\prime }}\left(\chi ,{\chi }^{\prime }|k\right)e_{{\alpha }^{\prime }}\left({\chi }^{\prime }\right)$ (20)

其中，D为格点表象中的晶格动力学矩阵，其矩阵元为 [10]

$D_{\alpha {\alpha }^{\prime }}\left(\chi ,{\chi }^{\prime }|k\right)=\frac{1}{m}\underset{l^{\prime }}{{\displaystyle \sum }}{\Phi }_{\alpha {\alpha }^{\prime }}\left(l\chi ,l^{\prime }{\chi }^{\prime }\right){\text{e}}^{-iak\cdot \left[R\left(l\right)-R\left(l^{\prime }\right)\right]}$ (21)

将硅晶体中的力常数矩阵代入(21)式，得以下格波表象中的硅单晶的晶格动力学矩阵元

$\begin{array}{l}{D}_{xx}\left(1,1|k\right)=D_{xx}\left(2,2|k\right)\\ =4\frac{\mu }{m}\cos \frac{k_{x}a}{2}\left(\cos \frac{k_{y}a}{2}+\cos \frac{k_{z}a}{2}\right)+4\frac{\lambda }{m}\cos \frac{k_{y}a}{2}\cos \frac{k_{z}a}{2}-\left(4\frac{\alpha }{m}+4\frac{\lambda }{m}+8\frac{\mu }{m}\right)\end{array}$ (22)

$\begin{array}{l}{D}_{xy}\left(1,1|k\right)=D_{yx}\left(2,2|k\right)=D_{yx}^{\text{*}}\left(1,1|k\right)=D_{xy}^{\text{*}}\left(2,2|k\right)\\ =-4\frac{\nu }{m}\sin \frac{k_{x}a}{2}\sin \frac{k_{y}a}{2}+4i\frac{\delta }{m}\sin \frac{k_{z}a}{2}\left(\cos \frac{k_{x}a}{2}-\cos \frac{k_{y}a}{2}\right)\end{array}$ (23)

$\begin{array}{l}{D}_{xy}\left(1,2|k\right)=D_{yx}^{\text{*}}\left(2,1|k\right)=D_{yx}\left(1,2|k\right)=D_{xy}^{\text{*}}\left(2,1|k\right)\\ =\frac{\beta }{m}\left[1+{\text{e}}^{-i\left(k_x+k_y\right)a/2}-{\text{e}}^{-i\left(k_y+k_z\right)a/2}-{\text{e}}^{-i\left(k_z+k_x\right)a/2}\right]\end{array}$ (24)

$D_{xx}\left(1,2|k\right)=D_{xx}^{\text{*}}\left(2,1|k\right)=\frac{\alpha }{m}\left[1+{\text{e}}^{-i\left(k_y+k_z\right)a/2}+{\text{e}}^{-i\left(k_z+k_x\right)a/2}+{\text{e}}^{-i\left(k_x+k_y\right)a/2}\right]$ (25)

用以上方法同样可以计算得到 $D_{yy}\left(1,1|k\right)$ 和 $D_{yy}\left(2,2|k\right)$，或 $D_{zz}\left(1,1|k\right)$ 和 $D_{zz}\left(2,2|k\right)$； $D_{yz}\left(1,1|k\right)$、 $D_{zy}\left(2,2|k\right)$、 $D_{zy}^{\text{*}}\left(1,1|k\right)$ 和 $D_{yz}^{\text{*}}\left(2,2|k\right)$，或 $D_{zx}\left(1,1|k\right)$、 $D_{xz}\left(2,2|k\right)$、 $D_{xz}^{\text{*}}\left(1,1|k\right)$ 和 $D_{zx}^{\text{*}}\left(2,2|k\right)$； $D_{yz}\left(1,2|k\right)$、 $D_{zy}^{\text{*}}\left(2,1|k\right)$、 $D_{zy}\left(1,2|k\right)$ 和 $D_{yz}^{\text{*}}\left(2,1|k\right)$，或 $D_{zx}\left(1,2|k\right)$、 $D_{xz}^{\text{*}}\left(2,1|k\right)$、 $D_{xz}\left(1,2|k\right)$ 和 $D_{zx}^{\text{*}}\left(2,1|k\right)$； $D_{yy}\left(1,2|k\right)$ 和 $D_{yy}^{\text{*}}\left(2,1|k\right)$，或 $D_{zz}\left(1,2|k\right)$ 和 $D_{zz}^{\text{*}}\left(2,1|k\right)$，经过将它们分别与(22)式、(23)式、(24)式和(25)式比较发现，它们可以分别由以上相应各式将x、y和z分别变为y、z和x，或z、x和y而得到，这与硅单晶的晶体结构是一致的，这也在一定程度上证明了本文的计算得到的晶格动力学矩阵是正确的。

由以上矩阵元可组成6阶的晶格动力学矩阵 $D\left(k\right)$，对应于每一个波矢 $k$，求解晶格动力学的本征值问题，可以得到6个本征值 ${\omega }_j^2\left(k\right)$ 和对应的单位本征矢 $e\left(\chi |kj\right)$，其分量为 $e_{\alpha }\left(\chi |kj\right)$，其中， $j=1,2,\cdots ,6$。量子化后，晶格原子位移和晶格振动哈密顿可分别表示为

$u_{\alpha }\left(l\chi \right)=\underset{kj}{{\displaystyle \sum }}\sqrt{\frac{\hslash }{2Nm{\omega }_j\left(k\right)}}{e}_{\alpha }\left(\chi |kj\right)A_j\left(k,t\right){\text{e}}^{iak\cdot R\left(l\right)}$ (26)

其中 $A_j\left(k\right)=a_j\left(k\right)+a_j^{+}\left(-k\right)$，为声子产生和消灭算符。

$H=\underset{kj}{{\displaystyle \sum }}\left[a_j^{+}\left(k\right)a_j\left(k\right)+\frac{1}{2}\right]\hslash {\omega }_j\left(k\right)$ (27)

4. 硅单晶比热计算与讨论

根据(27)式可得硅单晶的晶格振动内能公式

$E=\underset{kj}{{\displaystyle \sum }}\left({\bar{n}}_{kj}+\frac{1}{2}\right)\hslash {\omega }_j\left(k\right)$ (28)

其中， ${\bar{n}}_{kj}$ 为声子布居数即平均声子数，符合玻色统计：

${\bar{n}}_{kj}=\frac{1}{{\text{e}}^{\hslash {\omega }_j\left(k\right)/k_{B}T}-1}$ (29)

设硅单晶中共有N个原胞，因每个原胞中有2个原子，则硅单晶质量为2Nm，根据比热定义可得以下比热公式

$C=\frac{1}{2Nm}\underset{kj}{{\displaystyle \sum }}\frac{{\bar{n}}_{kj}}{\partial T}\hslash {\omega }_j\left(k\right)$ (30)

由(29)式和(30)式可知，当温度 $T\to 0\text{K}$ 时， $\partial {\bar{n}}_{kj}/\partial T\to 0$，因此在极低温下，硅单晶比热为零；而当温度 $T\gg \hslash {\omega }_j\left(k\right)/k_B$ 时， $\partial {\bar{n}}_{kj}/\partial T\to k_B/\hslash {\omega }_j\left(k\right)$，因此在高温下，硅单晶比热逼近于常数 $3k_B/m$，即888.03 J/K/kg。

由于在前面的所有推导和计算，都建立在原子在其平衡位置附近作小幅振动的假设的基础上的，因此只考虑了二阶势能亦即采用了和谐近似，并没有考虑三阶以上的非和谐势能项，所以有关比热公式和结果不适用于极高温的情况。对于极高温情况下出现的非和谐势能，可用量子力学中的微扰论加以解决 [8]。

求解晶格动力学矩阵的本征值问题得声子频率 ${\omega }_j\left(k\right)$，再用(30)式计算0 K到1400 K温度下硅单晶的比热，以及在极高温下比热逼近于常数 $3k_B/m$ 的渐近线。在图1中，为了判断本文计算结果的准确性，在该图中还列出了Shanks等人 [11] 和Anderson等人 [12] 的实验数据。由图1可知，在温度低于800 K的情况下，我们的理论计算结果与他人的实验数据很好地吻合，这既说明了在非极高温度的情况下，原子热振动幅度不大，因而非线性相互作用不明显，可以用在和谐近似下推导得到的比热公式进行计算，也说明了我们运用Rignanese等人用第一性原理计算得到的最近邻和次近邻原子间个数有限的相互作用力常数，所得到的完整的线性力常数矩阵是正确的，并且在此基础上得到的晶格动力学矩阵也是正确的；而当温度为800 K时，我们的计算结果与Shanks等人的实验数据略有偏离，并该偏离随温度的升高会继续加大，这主要是因为当温度较高时，非线性相互作用开始显现，而我们在公式的推导和比热的计算过程中都采用了和谐近似，并没有计入非和谐势能的影响。幸运的是，在工程实践中，硅基器件的使用温度一般远低于800 K，因此我们的模型与公式可以得到有效使用。

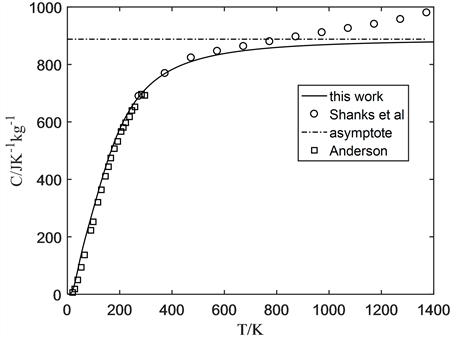
Figure 1. The specific heat of silicon single crystal vs temperature

图1. 硅单晶比热与温度的关系

5. 结论

本文推导了完整的晶格动力学力常数矩阵和晶格动力学矩阵，在此基础上运用Rignanese等人计算得到的最近邻和次近邻原子间有限数量的相互作用力常数，即可求解晶格动力学矩阵的本征值问题，得到晶格振动频率和单位极化矢量，并可得量子化后的晶格原子位移公式和晶格振动哈密顿公式，为用晶格动力学研究硅单晶热学性质做了必要准备。本文还计算了硅单晶的比热，发现在温度低于800 K的情况下，理论计算结果与实验结果能很好地吻合，但当温度增加至800 K时，理论计算结果与Shanks等人的实验数据开始有明显偏离，并该偏离随温度的升高会继续加大，但由于在工程实践中硅基器件的使用温度一般远低于800 K，因此我们的模型与公式可以得到有效使用。

NOTES

^*通讯作者。