1. 引言
近些年来,随着量子信息理论的不断发展,人们研究发现当纠缠为零时,系统仍然可以表现出量子关联特性,这就说明量子纠缠并不能包含量子系统中所有的量子关联。Ollivier和Zurek在2001年首次提出了量子失协 [1],并把它定义为量子互信息和经典关联之间的差,同时证明量子失协捕获了比纠缠更普遍的量子关联。此后,学者们对量子失协进行了大量研究,发现量子失协比量子纠缠更具有普遍性和优势。近年来,人们研究了在不同物理体系中的量子失协,其中包括自旋链 [2] [3]、原子系统 [4]、光子系统 [5]、量子点 [6] 等。另外,量子失协也被广泛应用于量子相变的研究 [7] [8]、量子态合并 [9] [10],在文献 [11] 中表明量子失协不仅是一种信息资源,也是一种物理资源,因为无论何时量子关联发生变化都应该伴随着系统和环境的熵的产生。并且更有趣的是,一些研究表明,即使纠缠突然消失,量子失协的动力学也能在很长时间内保持恒定值 [12]。前面对于量子失协的研究只是基于被测系统与测量仪器之间相互作用比较强的测量,如投影测量的条件下进行的,但是对于被测系统和测量仪器之间的相互作用很弱时,就需要讨论超量子失协。有研究已经证明,对于两体量子体系,在其中一个子系统上进行弱测量会导致超量子失协。
根据量子力学的传统解释,对量子系统的测量使它塌缩为一种不同于测量前的新状态,也就是说,量子测量过程在大多数情况下会改变被测系统的态。然而,弱测量作为一个理论方案被引入 [13],这允许我们在对研究系统造成最小影响的情况下探索量子系统 [14] - [19]。弱测量下的量子关联是一个新兴的研究课题,它的性质不同于投影测量 [20]。最近,有学者利用弱测量实验性地模拟了一个弱POVM对核磁共振量子信息处理器的影响 [21]。另一个有趣的课题是研究噪声环境中不同类型关联的动力学,量子关联的动力学行为的知识将有助于我们理解和设计合适的方式来保护信息处理过程中的关联。量子系统与其环境之间不可避免的相互作用会破坏系统之间的量子关联,并导致有用资源的减少。防止量子关联衰减,从而抵抗退相干,这对于有效的实现量子信息处理是非常重要的。因此,理解噪声环境中子系统之间量子关联的动力学对于量子信息和量子计算是至关重要的。
尽管关联动力学在耗散环境中的量子系统已经被广泛的研究,但仍然存在的问题是弱测量环境对量子失协有何影响。在这篇论文中,我们只关注两个非相互作用的两能级原子,每个原子都被独立地放置在一个热库中,我们将研究热环境中两个原子之间量子失协的动力学。我们的主要目标是通过我们的模型来研究测量强度参数对量子失协的影响。我们的结果表明,在耗散环境下,弱测量可以揭示更多的两体系统量子态的量子关联。
2. 理论描述
为了讨论的完整性,下面我们对强测量下的量子失协和弱测量下的超量子失协做简要介绍。
2.1. 强测量下的量子失协
正交投影测量就是我们最常用到的强测量的一种,它又被称为Von Neumann测量。给定一个复合系统的状态
,标准量子失协被定义为总关联和经典关联之间的差,如下式所示:
(1)
其中总关联由量子互信息来度量,量子互信息被定义为:
(2)
是量子系统的Von Neumann熵,它描述了子系统a或b或者整个复合系统的不确定性:
(3)
下标j表示子系统a(b)或者整个系统,
和
是
的约化密度矩阵,
是量子态
的非零本征值。
是两量子系统的经典关联,经典关联被定义为:
(4)
其中,
是作用在子系统b上的一组完备的投影算符。
是子系统a在给定子系统b上完备集的量子条件熵,并且有
,
。因此,量子失协可以表示为:
(5)
2.2. 弱测量下的超量子失协
在弱测量下的量子失协,被Singh和Pati称之为“超量子失协”(SQD) [22],它实质上是在Von Neumann测量和POVM (正算符取值测量)的基础上发展起来的一种状态部分塌缩测量。
首先考虑测量算符。弱测量理论可以用Oreshkov和Brun的测量算符形式来表述 [23]。弱测量算符定义为:
(6)
其中x是测量过程中测量强度的参数,
和
是正交投影算符,并且
。
在超量子失协条件下,量子条件熵
被弱量子条件熵
代替,下标w表示用弱测量算符
对子系统b执行弱测量。进行弱测量以后,子系统a的状态为:
(7)
相应的概率为:
(8)
弱量子条件熵由下式给出:
(9)
因此,超量子失协被定义为:
(10)
其中
,即:
(11)
3. 分析与讨论
在本文的研究中,我们考虑两个非相互作用的两能级原子,它们分别被放置在两个空间分离的热库中,并且独立地与具有相同特征的热库相互作用,原子之间没有直接的相互作用。根据一般量子库理论 [24],我们可以推导出两能级原子与它们的局部热库相互作用的约化密度矩阵的运动方程:
(12)
其中
是局部热库的平均热光子数,
是原子
的自发辐射率,
是原子i的上升(
)和下降(
)算符,这里我们假设二能级原子和热库之间的关联时间比二能级原子动态演化的特征时间短得多,因此马尔可夫近似是有效的。等式(12)的解取决于两能级原子的初始状态。选取二量子体系中的基矢为
,
,
,
,我们考虑下面的二量子比特初始态:
(13)
其中
,并且有
。在这种状态下,Bell态
和激发态
是混合的。当
时,该状态是可分离态,当
时,该状态是最大纠缠态
。为了简单起见,我们假定
并且
。主方程(12)的解的矩阵元由下式给出:
(14)
除此以外其他矩阵元均为零。
为了研究耗散环境中弱测量下的超量子失协的动力学演化行为,我们将通过上述耗散模型研究测量强度参数和热效应对于量子关联的影响。在下面的讨论中,我们将强测量下的量子失协和弱测量下的超量子失协的动力学绘制成标度时间
的函数进行分析。根据上面的分析,我们可以画出量子失协和超量子失协的演化如下所示:
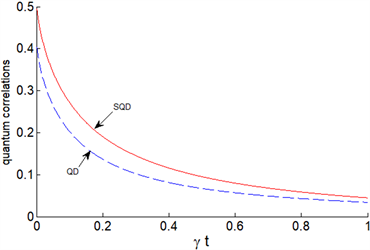 (a)
(a)  (b)
(b)  (c)
(c)
Figure 1. Dynamic evolution of two-atom quantum discord and superquantum discord. Solid line (red) represents super quantum discord, and dotted line (blue) represents quantum discord. In which parameters P = 0.5, x = 1 (a) n = 0.01; (b) n = 1; (c) n = 5
图1. 二原子量子失协与超量子失协的动力学演化。实线(红色)代表超量子失协,虚线(蓝色)代表量子失协。其中参数P = 0.5,x = 1 (a) n = 0.01;(b) n = 1;(c) n = 5
 (a)
(a) 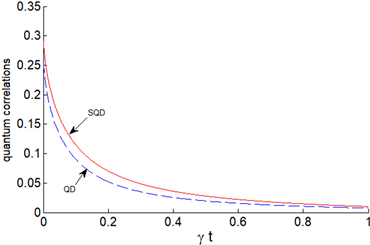 (b)
(b) 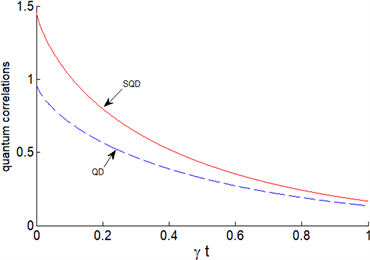 (c)
(c)
Figure 2. Dynamic evolution of two-atom quantum discord and superquantum discord. Solid line (red) represents super quantum discord, and dotted line (blue) represents quantum discord. In which parameters n = 0.1, x = 1 (a) P = 0.1; (b) P = 0.3; (c) P = 0.99
图2. 二原子量子失协与超量子失协的动力学演化。实线(红色)代表超量子失协,虚线(蓝色)代表量子失协。其中参数n = 0.1,x = 1 (a) P = 0.1;(b) P = 0.3;(c) P = 0.99
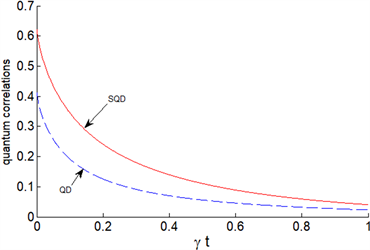 (a)
(a)  (b)
(b)  (c)
(c)
Figure 3. Dynamic evolution of two-atom quantum discord and superquantum discord. Solid line (red) represents super quantum discord, and dotted line (blue) represents quantum discord. In which parameters P = 0.5, n = 0.1 (a ) x = 0.1; (b ) x = 1; (c ) x = 5
图3. 二原子量子失协与超量子失协的动力学演化。实线(红色)代表超量子失协,虚线(蓝色)代表量子失协。其中参数P = 0.5,n = 0.1 (a ) x = 0.1;(b ) x = 1;(c ) x = 5
在图1中,当混合程度P和测量强度参数x取固定值,只改变平均热光子数n的取值,图中的曲线显示了标准量子失协和弱测量下的超量子失协的时间演化过程。首先,我们注意到两个量子关联都消失在渐近极限中,这是因为量子系统与其耗散环境产生了相互作用。当n取值很小,即耗散效应较弱时,两种关联的差异较大,衰减较慢。随着平均热光子数n的取值逐渐增大,耗散效应逐渐增强,两种关联的差异逐渐减小,并且衰减速度加快。
在图2中,将平均热光子数n和测量强度x取固定值,只改变混合程度P的值,我们发现,随着P值的增加,关联时间和初始值都在增加,衰减速度减慢。当P取值较小时,此时的系统接近于可分离态,两种关联的差异很小,而随着混合程度增大时,两种关联差异逐渐变大,且主要表现在初始时刻,这就说明混合程度的改变影响了两关联的初始值,随着混合程度逐渐增加,两种关联的差异也逐渐变大,衰减速度逐渐减慢。但是混合程度只取决于我们所选取的初始状态,并不是主要的影响因素,我们更多考虑外部环境和测量强度对两种关联的影响。
图3中我们考虑测量强度对于关联演化的影响。在这种情况下,我们固定混合程度P和平均热光子数n的值,只改变测量强度x的值。当x取值比较小时,两种关联的差异比较大,逐渐增大测量强度x的值,我们发现,随着x的增加两条曲线逐渐靠近,并且增大到某个值时,两条曲线近似重合,当
时,重合曲线不再发生变化,弱测量下的量子失协会成为Von Neumann测量下的量子失协,此时,弱测量就转化成了强测量。此外,我们注意到,图1和图2中不论P和n如何改变,量子失协总是小于超量子失协,并且清楚地表明,尽管量子失协和超量子失协之间存在差异,但两种失协的动力学在性质上表现出相似的行为。
一般来说,图1,图2和图3中的所有曲线都表明,在热环境下,两个量子关联都趋向于在渐近极限内消失。很明显,在热环境中,量子关联很容易被破坏,因此,我们可以推断出量子关联可以通过增加热场参数来消除。此外,我们在所有图中观察到,弱测量下的超量子失协总是大于标准的量子失协,这就意味着弱测量比强测量(投影测量)能捕获更多的两体量子系统的量子关联。换句话说,如果我们对一个系统进行微弱的量子测量,那么在子系统之间会有更多的量子关联,这些就可以用于实际应用。此外,我们所研究得到的这些结果还表明测量确实改变了量子失协的动力学行为。
4. 结论
在本文中,我们研究了耦合到独立热库的两个原子在弱测量下的超量子失协和强测量下的量子失协的动力学行为。主要通过改变测量强度参数和平均热光子数的值,讨论了它们的变化对量子关联的影响。从结果可以看出,随着耗散效应逐渐变弱,强测量下的量子失协与弱测量下的超量子失协之间的差异趋于增大,并且两种量子关联都消失在渐近极限内。我们特别研究了弱测量在两个量子比特量子失协演化过程中的作用。结果表明,强测量下的量子失协和弱测量下的量子失协的差异随着测量强度参数的减小而增大,这就意味着量子失协的动力学行为对测量强度参数很敏感,并且弱测量比强测量能捕获更多的两体量子系统的量子关联。