单原子层薄膜热传导性质的晶格动力学研究(II)——数值计算与结果分析

Lattice Dynamics Study on the Thermal Conduction Properties of Single Atomic Layer Films (II)—Numerical Calculations and Analysis on the Results

摘要: 本文在先前得到公式的基础上，对单原子层薄膜晶格的声子线宽、声子自由程和声子对热传导系数贡献与其波矢的关系进行了计算，并计算了薄膜热膨胀系数随尺寸的变化规律。计算结果表明，短波矢声子即低频声子具有较长的自由程，对热传导系数的贡献较大。当薄膜尺寸增加时，声子自由程分布越往低波矢区域集中，并且低波矢区域的声子自由程越大，短波矢声子即低频声子对薄膜热传导系数的贡献越大。薄膜尺寸越大，热传导系数越大，并且当尺度N超过40个晶格常数时，其热传导系数与尺寸的对数logN之间存在线性关系，当尺寸趋于无穷时，热传导系数趋于发散，因此大尺寸单原子层薄膜有卓越的散热性能。

Abstract: Based on the formulas derived previously by the authors, the variation of the phonon line width, phonon free path, the contribution of phonon to thermal conductivity with its wave vector are calculated. The results show that the phonon with a shorter wave vector, or with a lower frequency, has a longer free path and a greater contribution to the thermal conductivity. When the size of the film increases, the more phonon free path distribution is concentrated in the low wave vector region, the phonon free path in the low wave vector region is larger, and the contribution of the short wave vector phonon, that is the low frequency phonon, to the thermal conductivity of the film is bigger. The larger the size of the film, the larger the thermal conductivity, and when the size N exceeds 40 lattice constants, there is a linear relationship between the thermal conductivity and logN. When the size tends to infinity, the thermal conductivity tends to diverge, so single atomic layer film with large size has excellent heat dissipation performance.

1. 引言

学术界已经有许多用分子动力学方法模拟热传导性质的报导 [1] [2] [3] [4]，该方法建立在牛顿力学的基础上，通过对多原子的运动方程进行求解来计算热传导性质。但在参考文献 [5] 中，我们已经分析过分子动力学存在一些局限性，并通过晶格动力学和和Green函数等理论，推导得到了以下的单原子层薄膜的声子频率、群速度、声子线宽和热传导系数公式

${\omega }_k^2=\frac{2k}{m}\left(2-\cos k_{x}a-\cos k_{y}a\right)$ (1)

$v_k^x=\frac{ka}{m{\omega }_k}\sin k_{x}a$ (2)

${\Gamma }_k=\frac{72}{{\hslash }^2}\underset{k_1{k}_2}{{\displaystyle \sum }}\underset{\pm }{{\displaystyle \sum }}\left[\left({\bar{n}}_{k_2}+\frac{1}{2}\right)\pm \left({\bar{n}}_{k_1}+\frac{1}{2}\right)\right]\frac{\omega \left({\omega }_{k_1}\pm {\omega }_{k_2}\right)\left({\Gamma }_{k_1}+{\Gamma }_{k_2}\right){\left|V\left(k_1;k_2;-k\right)\right|}^2}{{\left[{\omega }^2-\left({\omega }_{k_1}\pm {\omega }_{k_2}\right)\right]}^2+{\left[2\omega \left({\Gamma }_{k_1}+{\Gamma }_{k_2}\right)\right]}^2}$ (3)

${\kappa }_x=\frac{3k_B{\beta }^2}{V}{\displaystyle \underset{k}{\sum }{\hslash }^2{\omega }_k^2{L}_k^x{v}_k^x{\bar{n}}_k\left({\bar{n}}_k+1\right)}$ (4)

本文将用以上公式，对声子频率 ${\omega }_k$ 、群速度 $v_k^x$ 、线宽 ${\Gamma }_k$ 、自由程 $L_k^x$ 以及单原子层薄膜沿x方向的热传导系数 ${\kappa }_x$ 进行计算，探究其热传导的性质及其规律。由于符合M-P模型的材料实际并不存在，它的意义在于结构简单，在这个模型上可以较为方便地研究材料的一些性质，因此这里综合、借鉴了其它一些材料的参数，准备用以下参数进行模拟：a为0.5432 nm，原子质量m为6.63 × 10⁻²⁶ kg，线性力常数k为0.1206 N/m，非线性常数 $\delta$ 为1.767 × 10¹⁰ N/m。

2. 声子色散关系与群速度

波矢在单原子层薄膜平面内的 $\sigma$ 方向波矢分量为 $k_{\sigma }a=2\pi n_{\sigma }/N$，其中 $\sigma$ 为x、y， $n_{\sigma }$ 为 $-N/2$， $-N/2+1,\cdots ,-1,0,1,2,N/2-1$。根据(1)式分别计算尺寸为 $N=40$ 和80的单原子层薄膜的各个不同波矢的声子频率，并在频率–波矢坐标系中，由这些离散的点连接而成频率–波矢关系曲面，如图1所示。由该图可知，在低频段即短波矢区域，声子频率与波矢 $k$ 大小成正比。由声子频率公式可计算其比例系数为 $a\sqrt{k/m}$，该比例系数即为低频声子的传播速度。由该图及(1)式还可知，当单原子层薄膜尺寸不同时，由于声子的色散关系并没有发生变化，因此声子频率与波矢关系曲面形状相同，只是曲面上的格点疏密不同。

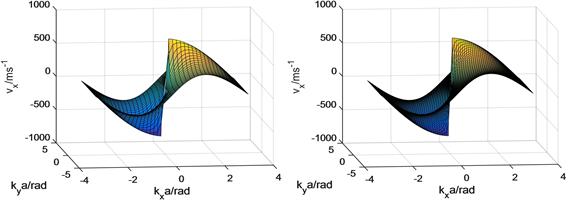
根据(2)式分别计算尺寸为 $N=40$ 和80的单原子薄膜的各个不同波矢的声子在x方向的群速度 $v_k^x$，并在群速–波矢坐标系中，将这些离散的点连接而构成群速–波矢关系曲面，如图2所示。由图可知，群速为正或负，分别对应于沿x方向的正向或反向传播，低频声子即短波矢声子的群速度较大。当单原子层薄膜尺寸不同时，由于由(2)式所决定的群速与波矢的关系并没有发生变化，因此声子群速与波矢关系曲面形状相同，只是曲面上的格点疏密不同。

(a) N = 40(b) N = 80

Figure 1. The phonon’s frequency vs. its wave vector

图1. 声子频率与波矢关系

(a) N = 40(b) N = 80

Figure 2. The phonon’s group velocity vs. its wave vector

图2. 声子群速度与波矢关系

3. 声子寿命与平均自由程

由声子线宽公式(2)式可以分别计算得到在100 K温度下尺寸为 $N=40$ 和80的单原子层薄膜的声子线宽 ${\Gamma }_k$ 与波矢 $k$ 间的关系，结果如图3所示。由图可知，波矢较小即声子频率较小时，声子线宽较小，并且随着波矢的减小，声子线宽继续减小，一直趋近于0，同时声子寿命 ${\tau }_k=1/{\Gamma }_k$ 持续增加，趋近于无穷。由图还可知，不同尺寸的单原子层薄膜，其声子线宽与波矢间的关系曲面具有相同形状，只是曲面上格点的疏密不同。

根据声子自由程公式 $L_k^x=v_k^x/{\Gamma }_k$，计算在100 K温度下尺寸为 $N=40$ 和80的单原子层薄膜的声子自由程与波矢间的关系，结果如图4所示。由图可知，短波矢声子即低频声子具有较长的自由程，并随着波矢的减小，其自由程增加，当声子的波矢接近0时，且声子线宽接近于0，其自由程接近于无穷。由图还可知，当单原子层薄膜尺寸增加时，声子自由程分布越往低波矢区域集中，并且低波矢区域的声子自由程越大。

(a) N = 40(b) N = 80

Figure 3. The phonon’s linewidth vs. its wave vector at T = 100 K

图3. 100 K温度下声子线宽与波矢之间的关系

(a) N = 40(b) N = 80

Figure 4. The phonon’s freepath vs. its wave vector at T = 100 K

图4. 100 K温度下声子自由程与波矢之间的关系

我们计算了在100 K温度下尺寸为 $N=40$ 和80的单原子薄膜， $k_{x}a=k_{y}a=\pi$ 的声子线宽收敛情况，结果如图5所示，可知，在迭代次数Ncount达5次时，声子线宽基本收敛。

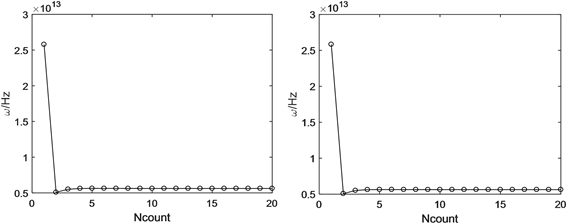(a) N = 40(b) N = 80

Figure 5. The Convergence of phonon’s linewidth at T = 100 K

图5. 100 K温度下声子线宽收敛情况

4. 单原子层薄膜热传导及尺寸效应

根据单原子层薄膜的热传导系数公式(3)式分别计算在100 K温度下尺寸为 $N=40$ 和80的单原子层薄膜不同波矢的声子对热传导系数的贡献，如图6所示。由图可知，波矢较小的声子即低频声子对热传导系数的贡献较大，并且波矢越小即声子频率越低，其对热传导系数的贡献越大；由图还可知，当单原子层薄膜尺寸增加时，短波矢声子即低频声子对薄膜热传导系数的贡献越大，并且相比于长波矢声子即高频声子，逐渐占据主导地位。

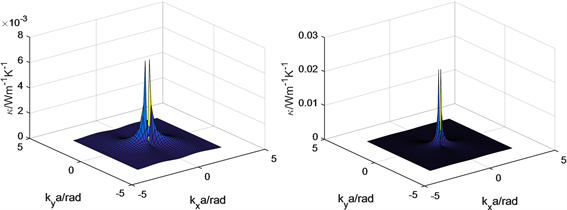(a) N = 40(b) N = 80

Figure 6. The phonon’s thermal conductivity vs. its wave vector at T = 100 K

图6. 100 K温度下声子热传导系数与波矢之间的关系

为了要检验热传导系数的迭代计算收敛情况，我们分别计算了在100 K温度下尺寸为 $N=40$ 和80单原子层薄膜的热传导系数收敛情况，结果如图7所示。由图可知，在迭代次数Ncount达5次时，热传导系数已经收敛。

(a) N = 40(b) N = 80

Figure 7. The Convergence of phonon’s thermal conductivity at T = 100 K

图7. 100 K温度下声子热传导系数收敛情况

为了研究单原子层薄膜热传导性质的尺寸效应，分别在100 K温度下对尺寸N为10、20、40、80、160、320和640的单原子层薄膜热传导系数进行计算，得热传导系数随尺寸N变化的规律，如图8图所示。由图可知，单原子层薄膜尺寸越大，热传导系数越大，并且当N超过40时，其热传导系数与尺寸满足线性关系 ${\kappa }_x=p1\ast \log N_x+p2$，其中 $p1=0.022881$， $p2=0.15357$，残差模为0.0010979。当尺寸趋于无穷时，热传导系数趋于发散。本文得到的单原子层薄膜热传导系数尺寸效应的规律与Xu等人 [4] 的实验结果描述的规律是一致的。综合以前我们对分子机器中链状分子热传导性质的理论研究的结论 [6]，我们发现，与块体晶体不同，一维和二维结构的热传导系数都随其尺寸增加而增加，当尺寸趋于无穷时，其热传导系数也趋于无穷，该结论对纳米机电系统和集成电路的散热设计有重要的指导意义。

Figure 8. The thermal conductivity vs. size of single atomic layer film at T = 100 K

图8. 100 K温度下热传导系数与尺寸的关系

5. 总结与讨论

本文利用先前得到的公式的基础上，对单原子层薄膜晶格振动声子线宽、声子自由程、声子对热传导系数贡献与其波矢的关系，以及薄膜热传导系数的尺寸效应进行了计算，并解释了其物理机制。计算结果表明，短波矢声子即低频声子具有较长的自由程，对热传导系数的贡献较大。当单原子层薄膜尺寸增加时，声子自由程分布越往低波矢区域集中，并且低波矢区域的声子自由程越大，短波矢声子即低频声子对薄膜热传导系数的贡献越大，逐渐占据主导地位。单原子层薄膜尺寸越大，热传导系数越大，并且当尺度N超过40个晶格常数时，其热传导系数与尺寸 $\log N$ 满足线性关系，当尺寸趋于无穷时，热传导系数趋于发散，即大尺寸单原子层薄膜有卓越的散热性能，该结论对纳米机电系统和集成电路的散热设计有重要的指导意义。