1. 引言
支持向量机是一种机器学习方法,主要针对小样本分类问题开展的一种学习方法,遵守结构风险极小化原则,获取全局最优解,并在压缩感知、模式识别以及图像处理等热点领域中得到了广泛的应用。半监督支持向量机是一种能够同时兼顾标签与无标签样本的学习方法,因而半监督支持向量机的学习方法在处理大规模数据识别与分类的过程中处理良好。半监督支持向量机的数学模型优化问题较为复杂,在处理非线性分类问题时比较消耗时间,因此对半监督分类的模型与算法进行研究与设计非常重要。
2. 半监督支持向量机
2.1. 支持向量机
训练样本集为
,任意
,
,
,m表示样本特征的维数,l表示样本训练的个数。如果训练样本集是线性的,支持向量机需要满足条件
,则:
(1.1)
根据公式(1.1),能够得到
,如图1所示,图中的三角标志和圆圈表示的是两种不同类型的样本点,实线表示分类超平面,虚线表示支撑超平面 [1],两条虚线支撑超平面分别表示:
,
。
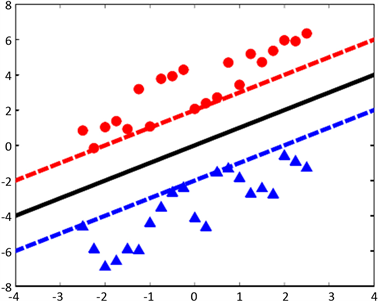
Figure 1. Linear Separable Support Vector Machine
图1. 线性可分支持向量机
2.2. 半监督支持向量机方法
在半监督支持向量机中,需要考虑到标签训练样本集和无标签样本集两种方式,分别为
和
,
,
,如图2所示,实心表示标签样本,空心表示无标签样本,无标签样本更能够体现出样本集的实际分布状况 [2]。
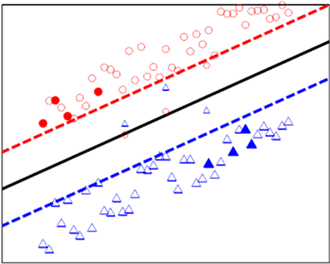
Figure 2. Semi-supervised support vector machines
图2. 半监督支持向量机
将未知的样本类标签看成是一种新的变量,能够得到半监督支持向量机的模型:
(1.2)
其中,
,
表示标签样本与为标签样本之间的惩罚参数。
在半监督分类过程中,为了避免类标签偏差较为明显,可以引入公式:
(1.3)
r表示所占比例。
公式(1.2)的求解方式有组合优化方式和连续优化方式,这两种方式的求解思想为:
组合优化方式中需要考虑
的取值可能性,对每一组固定的
进行取值,将公式(1.2)转化为标准的求解支持向量机的问题。对
的所有取值可能性进行遍历,得到相应的优化求解方式:
(1.4)
公式(1.4)属于混合正数规划问题,求解的方式较为困难。
在连续优化方法中,固定的数值在面对任意的
时,都可以使用
表示,得到关于固定数值的连续优化问题:
(1.5)
其中
,公式(1.5)属于一个非凸优化问题,该问题中的平衡约束可以表示为:
(1.6)
3. 半监督支持向量机的锥松弛方法
锥规划问题有着其特殊的结构方式,有较好的表述能力,在实际问题的解决中得到了广泛的应用于推广。本节介绍的半监督支持向量机的锥松弛方法,在原问题的基础上提出新的问题,并估计原问题的最优质与最新半正定松弛问题的比值,同时数值实验的结果证明松弛方法所取得的分类效果。
3.1. 半正定松弛
根据引理结论“若
和
成立,则
”,则
(2.1)
将公式(2.1)的目标函数进行转化,为:
(2.2)
引入变量
,公式(2.1)等价于 [3]:
(2.3)
该问题是含有凸与非凸的二次规划问题。
3.2. 双非负松弛
公式(2.1)的双非负松弛问题,在解决这类较难的非凸二次规划问题时,首先需要给出问题的完全正松弛。
令
,问题(2.1)能够被等价转换为 [4]:
(2.4)
其中,
,则:
(2.5)
公式(10)的目标函数可以进行转化,相应的等价问题为:
(2.6)
3.3. 数值实验
通过数值实验测试的方式对上述两种方法的分类表现进行记录,并将测得的试验结果与半监督支持向量机进行比较,对标签样本个数的分类精度影响进行重点的分析与实验。
选择两组人工数据,四组基准数据这六组数据集进行试验,如图3所示。具体的数据集信息如表1所示。

Figure 3. Artificial Data Set Sample Point Distribution and Classification Hyperplane
图3. 人工数据集样本点分布与分类超平面
首先,对半正定松弛与双非负松弛进行分类,根据图3所示的平面得到两组人工数据集的分类决策函数。其次,使用半正定松弛与双飞负松弛这两种方法对基准数据进行分类,记录使用这两种方式对采集到的数据集分类精度的最佳数值,其数值对比结果如表2所示,从表2可以看出,双非负松弛问题比半正定松弛所得到的分类精度更好更准确 [5]。

Table 2. Comparison results of positive semi-definite relaxation method and twin non-negative relaxation method
表2. 半正定松弛方法和双非负松弛方法对比结果
结果UCI数据集,对比半监督支持向量机与半正定松弛、双非负松弛,在对比的过程中采取的方法有梯度下降法、凹凸过程法等,不同对比方法的错分率结果如图4所示。
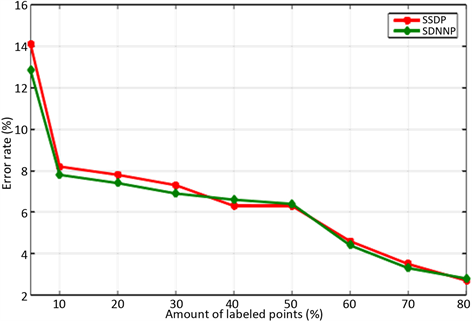
Figure 4. The influence of the number of labeled sample points on the error rate
图4. 有标签样本点个数对错分率的影响
本节提出的半监督支持向量机所对应的规划问题,其中介绍的两种锥松弛方法都能够得到元混合正数规划问题,通过进一步的分析能够得到更好的下届,通过数值实验的数据结果显示,这两种松弛方法都能够得到较好的分类效果,且双非负松弛比半正定松弛的分类精度更高更准确。
4. 多视角双平面支持向量机
将双平面支持向量机进行扩展,升级为多视角双平面支持向量机,在同一视角中,正样本与负样本由矩阵
表示,在另一个视角中,正样本与负样本
表示,为了使公式变得更加简洁,将所有的e表示为1的向量,都是合适维数的数值 [6]。即:
(3.1)
公式(3.1)中的
表示+1参数,
是−1参数。
多视角双平面支持向量机的优化问题可以表示为:
(3.2)
是全为1的向量,这些向量均是合适维数的数值,
表示分类器参数,
表示非负参数。对公式(3.2)用拉格朗日公式表示为:
(3.3)
表示拉格朗日向量。对公式(3.3)求偏导,使公式结果等于0,可以得到:
(3.16)
得到对偶问题:
(3.4)
在进行计算的过程中要注意一个分类准则 [7],对于同一个样本x,有两个不同的视角,如果
,
,则该公式属于+1类,否则为−1类,多视角半监督双平面支持向量机能够解决二次优化问题,但是它的复杂度较高,有两个不同视角的维数。
5. 半监督支持向量机学习分类方法
5.1. 优化方式分类
5.1.1. 组合优化方式
组合优化方式能够同时优化三个参数,分别为
,其中
的值能够通过人为的方式进行指定。即:
(4.1)
采用指定的方式就可以像优化标准的支持向量机一样,对组合方程进行优化。这种组合的方式可以供很多的优化算法进行使用,将组合优化方式应用在文本分类中,但是这些都是局部优化,无法对全局最优化起到一定的作用。
5.1.2. 连续优化方式
连续优化方式首先需要通过固定的参数
,寻找到代价函数最小的值:
,用指定标签值符号
进行表示,然后重复步骤标注其他的符号。即:
(4.2)
通过公式(4.2)能够看出,前两项是标准的支持向量机,最后一项是用二次代价函数进行代替,是一个非凸优化,如图5所示。
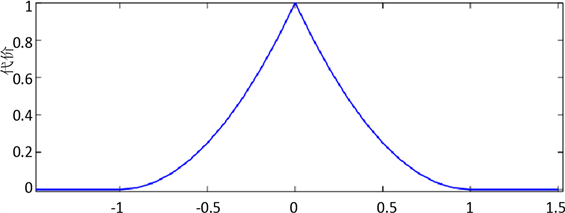
Figure 5. Symbolic output of decision function
图5. 决策函数的符号输出
5.2. 凹凸优化过程
凹凸优化过程采用的是半监督连续优化的方式,优化的方式就是将方程
中的最后一项进行分解,将其分解成凸函数与凹函数,在后面的迭代过程中,将这个凸函数替换为线性函数 [8],这种替换的方法叫做切线近似法,这样在迭代的过程中就只是一个凸函数和线性函数的计算,在进行求解的过程中较为简单。即:
(4.3)
为了可以达到优化的最终目的,可以将代价函数的值应用在目标方程中,这样就可以通过迭代的方式进行求解,从而得到最优解。对方程式作进一步的分类过程中,可以指定其中一个无标签的值为正数,并将其应用到训练的下一次迭代中,对结果目标方程所造成的影响为:
(4.4)
使用凹凸优化方法应用在半监督算法计算中,可以按照以下流程进行计算:
首先用监督支持向量机标签样本得到参数值
;
(4.5)
使用凹凸优化方法的优势就是能够对原来的非凸函数进行替换,将其替换成凹凸函数之和,大大简化了求解的复杂程度;但是存在的缺陷就是无法更好的利用原有的样本分布信息。
5.3. 基于标签传递的分类方法
采用标签传递的方式进行分类,标签传递的分类方法相当于聚类方式直接进行无标签样本分类,并与原数据进行训练,从而得到最终的决策函数,其主要的思想可以表示为 [9]:
对所有有标签的样本和无标签的样本进行构图,如果构建的图距离原来的标签样本越来越近,则说明与标签样本的类别相似,可以表示为:
(4.6)
表示图中样本点距离。
表示无标签样本,通过迭代求解的方式让其收敛,然后在
中选择其他类的无标签样本,并指定为该类别。其优势就是考虑到训练样本中存在的流形,采用构图的方式进行聚类,然后使用分类器进行整体分类;但是缺陷就是构图完成后,这张图的效果是影响整个作品的关键,只能够通过寻找这种流形的方式进行聚类,在构图的过程中选择相邻点容易出现模糊的情况,对分类精度的标签样本影响较大。
基于相似度标签传递的半监督支持向量机
半监督分类算法有聚类假设和流形假设两种方式,有标签的训练样本无法更好的描述整个样本空间的实际情况,如果只是用标签样本进行训练则分类的精度较低,不能更好的更新更多的数据。而大量的无标签样本则有可能更好的反映出整个样本空间的真实情况。因此,引入无标签样本能够更好的指导分类器的整个训练过程,从而提高分类器的精度。在进行标注的过程中,如何选择无标签样本则是需要重点考虑的问题。可以通过迭代的方式进行标注,通过其纠错能力解决这个问题。
用训练样本构建一个相似度图,数据表示节点,对所有的数据进行连接,如果两点之间的相似度较大,则相应的权值就越高,计算方法为 [10]:
(4.7)
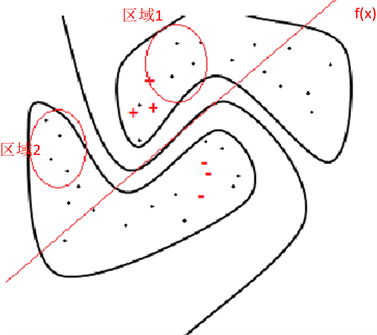
Figure 6. Approximately filter points with the same label according to similarity
图6. 按照相似度近似筛选可能相同标签的点
通过该公式构建了一个含有所有样本点的矩阵,该矩阵会受到t的影响,在取值的过程中需要适当的考虑向量机中径向基核函数的参数。
在进行标签传递的过程中,可以使用相似度的方式进行数据点的筛选,类似于聚类思想中的标签,但是与聚类思想不同的是在开始时没有使用聚类思想进行类别的划分,而是通过归纳式的支持向量机的方式进行结果的训练,将其作为标签传递的方向,并找到所有与其类别相同的数据点,这样做的目的就在于必须限定正负类比例的问题,才能够更好的完成数据的分类。通过新的标签样本重新定义决策函数,这种逐渐加入的样本信息,能够让决策函数变得更加完善。如图6所示。
6. 结束语
对提出的半监督支持向量机规划问题中所采用的两种凸锥松弛方法,能够更好地得到原混合正数规划问题的下界,从而得到更为准确的下界。对半监督支持向量机的分类方法进行了讨论与研究,在标签样本较少的情况下,可以使用无标签样本的方式提高分类的准确度,并在支持向量机的基础上进一步学习半监督学习方法。改进的半监督学习分类算法在失去平衡的情况下依旧能够发挥出其作用,用标签传递的方式对无标签样本进行标记,并在可能出现错误的地方进行标注和纠错,从而寻找到无标签样本中更合适的比例。
基金项目
新疆师范大学优秀青年教师科研启动基金资助项目(XJNU202012)。