1. 引言
洪水预报对防洪减灾、合理规划水资源等方面具有重要的指导意义 [1]。由于水文过程具有高度非线性、随机性和多峰分布等特征,以确定的表达方式描述不确定的水文过程存在较大偏差 [2],导致模型输出的预报值存在较大不确定性 [3]。近年来,数值降水预报被证实可以有效延长洪水预报的预见期 [4],为解决传统预报中实测降雨量难以满足工作需要的问题提供了可能,提高了较高预见期内洪水预报的精度。以概率形式量化不确定性的集合预报(ESP)系统被证实是减少不确定性的有效工具。不同来源的不确定性需要特定的方法来解决 [5],仅对模型输入及参数施加扰动,ESP系统无法改善模型固有的结构误差 [6],采用多模型水文集合预报可以考虑并减少模型结构带来的不确定性。代刊 [7] 等指出集合预报结果常出现系统性偏差及欠离散或过离散等问题,需要通过统计后处理方法予以校正。近年来,贝叶斯模型平均方法(BMA)广泛应用到多模型集合预报中,可以综合考虑模型输入、参数和模型结构的不确定性 [8]。董磊华 [9] 等利用BMA方法推求出新安江、SIMHYD和SMAR模型的预报值后验分布,发现BMA方法不仅提高了预报精度,还能推求出可靠的预报区间。但BMA方法以假定实测和预报流量服从正态分布为前提,需要对其进行正态转换处理 [10],如Box-Cox等方法,计算过程繁琐且容易产生随机误差和计算误差。与传统的基于正态分布的BMA方法相比,Sloughter [11] 等提出了改进的BMA方法(M-BMA),引入了Gamma分布,并考虑了零值,应用到风速等非正态分布变量的概率预报中。巴欢欢 [12] 等在三峡入库洪水集合概率预报中对比分析了集合输出统计模型(EMOS)、BMA、基于Copula函数的BMA (Copula-BMA)和M-BMA方法的应用效果,结果表明M-BMA方法能够考虑预报分布的异方差性,且不需要正态变换,确定性预报和概率预报效果最优。对于水文预报后处理对象,多数研究针对模型模拟值进行统计后处理,对考虑预见期内数值降水预报的多模型预报值进行统计后处理研究较少。
本文以陆水水库为研究对象,采用欧洲中期数值气象预报中心的降水预报数据,驱动API、新安江、GR4J三个模型,获得3 h、6 h、9 h、12 h预见期的陆水入库流量预报值。采用BMA和M-BMA方法对流量预报结果进行后处理,得到确定性的综合预报值和置信度90%的预报区间,并与单一模型预报结果进行对比,以此考虑不同预见期内模型结构的不确定性对洪水预报的影响及两种统计后处理方法对洪水预报的有效性。
2. 研究方法
2.1. 贝叶斯模型加权平均方法
贝叶斯模型平均方法是对预报成员的分布函数加权平均,降低预报量的不确定性,得到更为可靠的后验分布函数,其原理如下:
(1)
式中:h是预报量;H表示实测流量;k是模型个数;
是各个模型的预报值;
是给定实测数据H,第i模型预报值
的后验概率,反映了预报值与实测流量的匹配程度,可视为BMA方法的权重
,
。预报结果越好,其所分配的权重就越大;
是给定第i模型预报值
和实测数据H,预报量h的后验概率密度。
在实际应用中,径流系列往往不服从正态分布,需要采用Box-Cox转换法,将偏态变量转换为正态变量,具体公式如下:
(2)
式中:
为Box-Cox变换系数,
为正态变换后的变量。
Sloughter [11] 等对BMA方法进行了改进,假设非正态分布变量服从Gamma分布,即公式(1)中的
可由Gamma分布概率密度函数来表达:
(3)
式中:
代表伽马函数;
分别为伽马分布的参数,可根据变量的均值和方差进行计算:
(4)
在M-BMA方法中,分布的统计参数均值和标准差可以由各个模型的预报值估计得到:
(5)
式中:
是每个模型的预报值;
分别是需要估计的参数;其中
可通过线性回归进行估计得到,假定每个模型的
是相同的,即为
。
M-BMA方法的表达式为:
(6)
式中:
为每个模型预报值的权重。
两种统计后处理方法得到后验概率预报的期望值作为确定性预报结果,并且可以与集合预报成员进行对比,期望值采用下式计算:
(7)
有相关研究表明,基于正态分布的BMA方法在采用期望最大化(EM)算法估计参数时具有较强的鲁棒性,在应用BMA方法变种时采用全局优化算法较为合适 [13]。因此,BMA和M-BMA方法的参数分别采用EM算法和拟牛顿法中的BFGS算法进行估计,BFGS算法的优化目标函数为连续概率排位分数(CRPS)。
2.2. 模型评价指标
采用纳什效率系数(NSE)和径流总量相对误差(RE)以及平均绝对误差(MAE) 3个常用指标对确定性预报结果精度进行评价。采用Q-Q图、可靠性(α_index)和连续概率排位分数(CRPS)等指标来评定概率预报的性能。采用覆盖率(CR)、平均带宽(B)和单位平均相对区间宽度所包含的实测点据比例(PUCI)来评价预报置信区间的优良性。
2.2.1. 确定性预报
1) 纳什效率系数(NSE)
(8)
2) 径流总量相对误差(RE)
(9)
3) 平均绝对误差(MAE)
(10)
式中:
分别是t时刻实测流量和预报流量;
是实测流量均值。
NSE表明预报流量与实测流量模拟精度,NSE越接近于1,表明精度越高,模型方法越优。RE的绝对值越小,表明实测流量总量和预报流量总量误差越小。MAE表征预报流量与实测流量之间的平均误差,MAE越小,精度越高。
2.2.2. 概率预报
1) Q-Q图。Q-Q图通过比较预报值概率分布与实测值概率分布的差异,从概率角度检验预报概率分布的准确性 [14]。设第t个时段的预报累积分布函数为
,P值是第t个时段实测流量
对应的预报累积概率分布函数值,记为
。如果预报概率分布与实测值的概率分布相同,则
符合标准均匀分布
,对应于Q-Q图中的1:1线,否则就反映了预报概率的偏差。Q-Q图曲线越接近于1:1线,概率预报结果越合理。图1为概率预报Q-Q示意图 [15]。
2) 可靠性(α_index)。α_index用来定量描述可靠性的高低 [16],计算公式如下:
(11)
式中:
为P值的经验分位数,通过数学期望公式计算;
为通过标准均匀分布
计算得到的P值理论分位数。α_index取值为0~1,取值越接近1,表明概率预报可靠性越高。
3) 连续概率排位分数(CRPS)。连续概率排位分数是结合可靠性和集中度的综合指标,是评估概率预报结果总体效果的标准方法 [15],数学表达式为:

Figure 1. Schematic diagram of probability forecast Q-Q
图1. 概率预报Q-Q示意图
(12)
式中:
是第t时段预报流量的累积分布函数;
是第t时段的实测流量;积分变量r表示流量;
是实际流量的累积分布函数,当
时等于0,否则等于1。
当预报结果为单一确定性值时,CRPS变为平均绝对误差(MAE) [3]。CRPS指标是沟通确定性预报和概率预报的桥梁 [12],使得我们可以更加直观地比较确定性预报和概率预报结果的性能优劣,CRPS越低表示预报结果越好。
4) 覆盖率(CR)和平均带宽(B)。覆盖率是指预报区间覆盖实测流量数据的比率,是最常用的预报区间评价指标。
(13)
(14)
式中:n为预报区间覆盖的实测数据个数,T为总样本个数;
分别为第t时刻的预报区间的上界和下界。
5) 单位平均相对区间宽度所包含的实测点据比例(PUCI)
(15)
式中:RB为相对平均带宽,计算公式为
。PUCI是综合覆盖率和平均相对带宽评价预报区间优良性的指标。对于指定的置信水平,在保证有较高的覆盖率前提下,预报区间平均相对带宽越下越好。PUCI值越大,预报区间表现优良。
3. 水文模拟预报结果
3.1. 研究流域及数据
陆水为长江中游右岸一级支流,源出湘、鄂、赣三省交界的幕阜山北麓,流经湖北省通城、崇阳、蒲圻、嘉渔四县,于陆溪口汇入长江。干流全长约183 km,通城以下长约148 km,流域面积3950 km²,流域地势起伏较大,通城以上为上游,通城至陆水水库大坝为中游,以下为下游。上游为花岗岩山地峡谷区,中游为红砂岩宽谷,下游为平原。陆水水库控制面积3400 km²,占陆水流域面积的86.2%,水库总库容7.42亿m³,年均来水量33.02亿m³,是我国第一座混凝土预制安装试验坝,并以发电、灌溉为主,兼有防洪、养鱼、航运等综合效益。
采用陆水流域2012~2019年实测降水、蒸发和陆水水库入库流量资料,资料时段步长均为3 h。其中,陆水水库流域17个雨量站(白霓桥站、沙墩站、塘口站、路口站、施家塅站、新庄站、通城站、北港站、大沙坪站、高枧铺站、黄土塝站、崇阳站、以及崇阳~陆水水库区间的白霓桥站、崇阳站、洪下站和陆水水库站),分布密集且较为均匀,可用算数平均法计算流域面降水量。蒸散发资料来源于长江委水文局监测处提供的陆水水库E601型蒸发器观测数据。预见期内降水预报采用2014年~2019年汛期欧洲中期数值气象预报中心的6 h降水量累积预报网格数据,空间尺度为0.125˚E × 0.125˚N。由于下载的降水预报值时间尺度为6 h,采用数值平均获得3 h的降水预报数据。
3.2. 水文模拟结果分析
采用新安江、GR4J模型模拟陆水流域降雨径流关系。新安江有15个参数,且每个参数有很强的物理意义 [17]。GR4J模型是一个概念性降雨径流模型,仅含有4个参数,采用两个非线性水库进行产汇流计算 [18],模型结构简单,应用便捷。选用2012~2016年共5年数据作为模型率定期,2017~2019年共3年数据作为模型检验期。使用纳什效率系数和水量误差作为目标函数,并采用SCEM-UA算法对新安江和GR4J模型参数进行优化,模型计算步长为3 h。

Table 1. Calibration and verification results of Xinanjiang and GR4J models
表1. 新安江和GR4J模型的率定和检验结果
表1列出了新安江和GR4J模型的模拟结果。新安江模型率定期和检验期的纳什效率系数(NSE)分别为88.87%和89.34%,水量相对误差(RE)分别为−2.53%和5.07%;GR4J模型率定期和检验期的NSE分别为89.56%和91.91%,RE分别为−1.9%和3.79%,表明建立的新安江和GR4J模型对陆水水库入库流量模拟效果良好,水量误差较小,可应用于陆水水库入库流量预报。
3.3. 考虑降水预报的洪水预报结果分析
API模型由降雨径流相关图和单位线构成,属于多输入、单输出静态的系统数学模型 [19]。API模型是陆水水库实际作业预报采用的主要预报模型,使用效果良好。本文基于API、新安江、GR4J三个模型,以流域实测的面平均降水和欧洲中心数值天气预报数据作为输入,以2014~2019年汛期(5月1日~11月1日)每日8:00为基准点,计算得到预见期1~4个时段(时段为3 h)陆水水库入库流量的预报结果。表2列出1~4个时段预见期的API、新安江和GR4J模型预报入库流量的各项评价指标。
由表2可知,三种模型预报方案中,预报效果均为良好,其中,在各个预见期内,GR4J模型和新安江模型预报方案的各项指标表现相当,API模型预报方案效果相对较差。可以看出,API模型方案的相对水量误差较大,4个预见期的水量误差均超过29%,其他两种方案的相对水量误差均在11%以内。分析原因,可能是API模型在参数率定过程中通过人工结合计算机交互功能进行计算 [19],特别是在地下水分割时具有一定的主观性和随意性,从而出现模型模拟和预测过程出现不一致的情况,影响模型计算精度。此外,随着预见期的延长,输入及参数等不确定性不断放大及增加,预报精度也呈现出下降的趋势,符合客观实际的规律。

Table 2. Evaluation of flood forecasting results in Lushui Reservoir
表2. 陆水水库洪水预报结果评价
4. 集合概率预报结果评价
4.1. 自适应滑动窗口
水文过程受到降水特性、流域地理特征等不确定性因素的影响,水文时间序列常随季节变化发生周期性波动 [20]。因此,对于时变性较强的水文序列采用滑动窗口更新集合预报模型参数较为合适。滑动窗口基本思想是窗口随时间逐步向前滑动,不断舍弃旧数据和纳入新数据来更新模型参数 [21],使得模型参数随时序变化实时响应,提高模型自适应能力。为保证窗口能够较好的反映出序列的信息特征,本文以CRPS最小为目标,采用试算法优选不同预见期的窗口长度,试算范围为30~100个时段,步长为10个时段。经过试验综合分析,最优窗口长度为50个时段。
4.2. 集合概率预报期望值评价
采用BMA、M-BMA方法分别对三个模型的预报结果进行集合概率预报,并分析集合概率预报结果的可靠性和准确性,同时对比分析这两种统计后处理方法的有效性。
采用BMA、M-BMA方法得出预报量的后验概率分布函数(密度函数),并根据式(3)算得不同预见期后验分布的期望值。由表2可知,GR4J模型水量误差相对新安江模型较小,因此以GR4J预报值代表单一模型预报值与BMA、M-BMA方法期望值进行比较。以NSE、RE、MAE三个指标评价4个预见期时段的确定性预报结果。由表3可知,经BMA、M-BMA校正的预报值相较于原始确定性预报值,NSE、MAE指标均有所改善。BMA方法的NSE值提高0%~2.95%,MAE值降低6.58~9.82 m³/s;M-BMA方法的NSE值提高0.68%~3.07%,MAE值降低6.15~10.04 m³/s,但两种方法的RE值改善不明显。综合分析,两种统计后处理方法在一定程度上提高了预报精度。由各指标可知,M-BMA法期望值在不同预见期表现较优于BMA法。
图2给出了2019年6月4日~7月3日30天不同预见期原始确定性预报值和2个统计后处理期望值过程线,可以看出,原始确定性预报值偏大,期望值过程线与实测流量拟合效果较好,且两种方法得到的预报期望值差距较小,拟合效果均随着预见期的延长而降低。


Table 3. Comparison of deterministic forecast results in different lead times
表3. 不同预见期时段的确定性预报结果对比
4.3. 概率预报结果评价
为评价两种方法概率预报的可靠性,得出不同预见期内的Q-Q图、可靠性(α_index)指标。图3给出了两种方法不同预见期的陆水水库入库流量预报Q-Q图。依据图1中的评价方法,BMA和M-BMA方法不同预见期Q-Q曲线均接近于1:1线,说明概率预报整体表现良好,较好的捕捉了入库预报流量的不确定性,可靠性较高。可以看出BMA方法概率预报结果的可靠性略优于M-BMA方法。由α_index值可知,BMA和M-BMA方法α_index值均接近于完美值1,与Q-Q图的定性结果相对应,但两种方法差距较小,表明BMA和M-BMA方法的概率预报结果可靠性较高,概率预报分布可以较为清晰地模拟出实测流量概率分布的统计特征。
以覆盖率(CR)、平均带宽(B)、单位平均相对区间宽度所包含的实测点据比例(PUCI)来评价预报区间的优良性。表4列出了不同预见期置信度90%预报区间的评价指标结果,可以得知,BMA和M-BMA方法得到的不同预见期覆盖率CR值均超过83%,接近指定的置信水平90%,表明两种方法得到的预报区间基本可以包含实测资料,得到的预报区间较为可靠。随着预见期的延长,平均带宽B值逐渐增大,表明预报区间的精度下降,入库流量预报的不确定性增加。虽然BMA方法得到的覆盖率高于M-BMA方法,但它的预报区间宽度远远大于M-BMA方法,由综合指标PUCI可知,在不同预见期内M-BMA方法均高于BMA方法,表明覆盖率接近指定的置信水平90%的情况下,获得较高的集中度,M-BMA法得到的预报区间表现较为优良。因此,90%置信区间可以为防洪决策提供更多的信息,能够定量考虑不确定性,实现水文预报与防洪决策的有机结合。

Table 4. Evaluation index value of 90% forecast interval for different leading times
表4. 不同预见期置信度90%预报区间评价指标值
以连续概率排位分数(CRPS)指标评价概率预报整体性能,通过考虑CRPS相对MAE的降幅,突出概率预报的有效性 [12]。由表4可知,相较于确定性预报指标MAE值,两种方法概率预报结果的CRPS均明显减小。M-BMA方法不同预见期内CRPS值降低幅度为32%~44%,BMA方法CRPS值降低幅度小于M-BMA方法,表明M-BMA方法改善效果较为明显。研究结果表明,随着预见期的延长,综合指标CRPS值也呈现不断增加的趋势,意味着概率预报的性能和总体效果略有降低。
 (a) 预见期3 h
(a) 预见期3 h 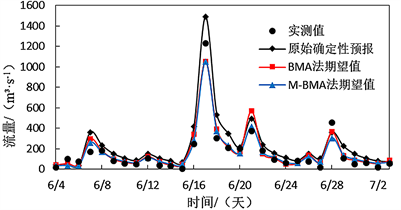 (a) 预见期6 h
(a) 预见期6 h  (c) 预见期9 h
(c) 预见期9 h  (d) 预见期12 h
(d) 预见期12 h
Figure 2. The deterministic forecast and the expected value of the two methods for different lead times
图2. 不同预见期确定性预报和两种方法期望值过程线
 (a) 预见期3 h
(a) 预见期3 h  (a) 预见期6 h
(a) 预见期6 h  (c) 预见期9 h
(c) 预见期9 h  (d) 预见期12 h
(d) 预见期12 h
Figure 3. Flow probability forecast Q-Q diagrams of BMA and M-BMA methods in different lead times
图3. 不同预见期BMA和M-BMA方法概率预报Q-Q图
综合各项指标可以发现,M-BMA方法在保证可靠性的情况下,具有较高的集中度和最佳的整体预报性能,因此M-BMA方法的预报性能优于BMA方法。这是由于自然状态下流量呈现偏态分布,正态转换处理过程复杂繁琐,在计算过程中难免加入计算误差和随机误差,导致部分信息失真,以偏态分布函数模拟较为合理;同时BMA方法没有考虑预报成员内的异方差性,容易导致集合成员分布函数离散性单一,从而出现PUCI值偏小等问题,而M-BMA方法通过建立方差与成员预报值的线性关系来实现异方差性,这也是M-BMA方法预报区间表现相对优良的原因之一。
5. 结论
本文综合考虑了陆水入库流量预报过程中的降水预报以及模型结构的不确定性,采用欧洲中心数值降水预报数据作为API、新安江以及GR4J模型的输入,建立了三种陆水入库流量集合预报方案,并基于BMA、M-BMA方法开展了陆水水库4个预见期的入库流量集合概率预报试验。得到以下结论:
1) 三种模型方案预报中,GR4J模型和新安江模型预报结果整体表现相当,API模型预报结果整体表现较差,但GR4J模型方案水量误差相对较小,新安江模型次之,API模型方案水量误差最大。
2) 纳什效率系数(NSE)等指标表明,经统计后处理方法校正过的预报值在一定程度上提高了预报精度。两种后处理方法得到的期望值预报效果差距较小,均与实测流量序列拟合效果较好,且优于确定性预报结果,随着预见期的延长,概率预报期望值的精度会相应降低。
3) BMA和M-BMA方法不同预见期覆盖率CR值接近指定置信水平90%,因此90%预报区间是可靠的,由PUCI指标可知,M-BMA方法的预报区间表现更为优良,可以为防洪决策提供更多的预报风险信息。随着预见期的延长,平均带宽逐渐增大,入库流量的不确定性增加。
4) BMA和M-BMA方法得出的概率预报分布均能较为可靠地模拟出实测流量概率分布的统计特征。由CRPS指标可知,经统计后处理的预报值的整体表现要优于确定性预报值,且可靠性较高;M-BMA方法相较于BMA方法整体表现更为优良。随着预见期的延长,两种方法的概率预报性能和总体效果降低。总体而言,M-BMA方法应用灵活,不需要正态变换,预报效果良好,有良好的研究前景。
基金项目
国家自然科学基金资助项目(51879192);湖北省自然科学基金资助项目(2020CFB239)。