基于MATLAB App Designer的汽车爬坡能力建模与仿真

Modeling and Simulation of Vehicle Climbing Ability Based on MATLAB App Designer

摘要: 本文基于汽车爬坡能力的理论基础，以某款轻型货车为例，对其相关参数进行匹配计算，利用MATLAB/ Simulink建立汽车爬坡能力计算模型，并结合MATLAB App Designer设计开发一款App，该程序可进行相关参数匹配计算并可绘制汽车爬坡度的仿真曲线，得到最大爬坡度、最大坡度角以及附着率，通过校验并确定轻型货车的爬坡能力。为汽车爬坡能力的确定，提供一款简便实用的工具。

Abstract: Based on the theory of automobile gradeability, taking a light truck as an example, matching cal-culation on its relevant parameters, the motor gradeability calculation model was established based on MATLAB/Simulink, and combined with MATLAB App Designer to design and develop an App, the program can match the relevant parameters and draw the simulation curve of automobile climbing degree, get the maximum climbing degree, the maximum slope angle and the attached rate, and verify and determine the climbing ability of light trucks. It provides a simple and practical tool for determining the climbing ability of automobile.

1. 引言

汽车常常需要在不同区域的不同道路上行驶，尤其在山区道路上，坡陡路窄，汽车必须具有一定的爬坡能力，爬坡能力通常由最大爬坡度来衡量，最大爬坡度是汽车动力性能的重要指标之一。为此开展了基于MATLAB App Designer的汽车最大爬坡度的研究。

2. 汽车爬坡能力的理论基础

汽车动力性通常由三个性能指标来评价，分别为汽车的最高车速、汽车的加速时间、汽车能爬上的最大坡度，汽车动力性是汽车的基本使用性能。汽车的爬坡能力是表征汽车极限运动的能力 [1]，也是汽车运动性能中较为重要的一项，而汽车最大爬坡度作为评价汽车爬坡能力的最为主要的参数，其数值的高低，对汽车的性能有着极其重要的作用。

2.1. 汽车发动机的相关参数

2.1.1. 汽车发动机转矩

根据汽车行驶速度和发动机转速之间的关系确定发动机转速n：

$n=\frac{u{}_{a}i{}_g{i}_0}{0.377r}$ (1)

式中，u_a为汽车的行驶速度(km/h)；n为发动机的转速(r/min)；r为车轮半径(m)；i_g为变速器传动比；i₀为主减速器传动比。

本文假设发动机的最低转速 $n_{\text{min}}=\text{6}00\text{r}/\text{min}$，最高转速 $n_{\text{max}}=4\text{0}00\text{r}/\text{min}$。

根据轻型汽车汽油发动机使用外特性的T_q-n曲线的拟合公式确定发动机转矩T_q：

$T_q=-19.313+295.27\left(\frac{n}{1000}\right)-165.44{\left(\frac{n}{1000}\right)}^2+40.874{\left(\frac{n}{1000}\right)}^3-3.8445{\left(\frac{n}{1000}\right)}^4$ (2)

式中，T_q为发动机转矩(N·m)；n为发动机转速(r/min)。

2.2. 汽车驱动力与行驶阻力

2.2.1. 汽车驱动力

汽车发动机产生的转矩，经传动系传至驱动轮上，此时作用于驱动轮上的转矩，产生一个对地面圆周力F₀，地面对驱动轮的反作用力即是驱动汽车的外力，此外力称为汽车的驱动力 [2]，其数值为：

$F_t=\frac{T_t}{r}$ (3)

作用于驱动轮上的转距是由发动机产生的转距经传动器传至车轮上的，即：

$T_t=T_q{i}_g{i}_0{\eta }_T$ (4)

式中，T_t为作用于驱动轮上的转矩(N·m)，r为车轮半径(mm)，T_q为发动机转矩(N·m)，i_g为变速器的传动比，i₀为主减速器的传动比，η_T为传动器的机械效率。

2.2.2. 汽车行驶阻力

假设汽车水平道路原地起步，且保持匀速，即汽车的加速度为0，由此可忽略坡道阻力和加速阻力，最后汽车受到阻力的只有空气阻力以及滚动阻力。

在汽车行驶过程中，受到的空气阻力为：

$F_w=\frac{1}{2}{C}_{D}A\rho u_r^2$ (5)

式中，C_D为空气阻力系数，ρ为空气密度(kg/m³)，A为迎风面积(m²)，u_r为相对速度(m/s)。

设定汽车处于无风条件下行驶，u_r即为汽车行驶速度u_a，则空气阻力为：

$F_w=\frac{C_{D}A{u}_a^2}{21.15}$ (6)

车轮滚动时，由于路面变形以及轮胎的弹性迟滞现象而产生滚动阻力，其数值为：

$F_f=G\times f$ (7)

式中，G为汽车的重力(N)，f为滚动阻力系数。

2.3. 汽车爬坡度与附着率

2.3.1. 汽车爬坡度

假设汽车在爬坡时保持匀速，即汽车的加速度为0。

汽车的爬坡能力是指汽车在良好路面上克服F_f + F_w后的余力，全部用来克服坡度阻力时能爬上的坡度，设定 $F_i=G\ast \sin \alpha$ 作为坡度阻力，则可求出汽车能爬上斜坡的坡度角 $\alpha$ 为：

$\alpha =\arcsin \frac{F_t-\left(F_f+F_w\right)}{G}$ (8)

2.3.2. 汽车附着率

附着率是反映汽车附着性能的重要指标，是在不打滑条件下，驱动轮能够充分发挥驱动力的最低地面附着系数 [2]。

设定汽车前轮驱动，汽车在爬坡时，前轮受到静态轴荷的法向反作用力，即：

$F_{Zs1}=G\left(\frac{b}{L}\cos \alpha -\frac{h_g}{L}\sin \alpha \right)$ (9)

式中：h_g为汽车质心高(m)，L为汽车轴距(m)，b为汽车质心至后轴的距离(m)。

当汽车加速和上坡时，可忽略空气阻力和滚动阻力，由此受到阻力的只有加速阻力以及坡度阻力，由此前轮受到的附着率为：

$C_{\phi 1}=\frac{F_i+F_j}{F_{Zs1}-\frac{G}{g}\frac{h_g}{L}\frac{\text{d}u}{\text{d}t}}=\frac{i+\frac{1}{\cos \alpha }\frac{1}{g}\frac{\text{d}u}{\text{d}t}}{\frac{b}{L}-\frac{h_g}{L}\left(i+\frac{1}{\cos \alpha }\frac{1}{g}\frac{\text{d}u}{\text{d}t}\right)}$ (10)

令 $i+\frac{1}{\cos \alpha }\frac{1}{g}\frac{\text{d}u}{\text{d}t}=q$，则前轮的附着率可简化为：

$C_{\phi 1}=\frac{q}{\frac{b}{L}-\frac{h_g}{L}q}$ (11)

式(10)中 $C_{\phi 1}$ 为汽车在爬等效坡时q所要求的附着率，当 $\phi >C_{\phi 1}$ 时，则附着率满足要求，当 $\phi <C_{\phi 1}$，则应重新计算，在实际地面附着系数 $\phi$ 的路面上能通过的最大等效坡度为 [3]：

$q=\frac{\frac{b}{L}}{\frac{1}{\phi }+\frac{h_g}{L}}$ (12)

3. 汽车爬坡能力建模及App设计开发

文章设定货车行驶在路面附着系数为0.7的路面上，根据上述理论计算公式，以某款轻型货车为例，其整车基本参数如表1所示，通过MATLAB/Simulink的搭建爬坡能力计算模型，并结合MATLAB App Designer开发设计出一款程序，以实现爬坡度的仿真计算。

Table 1. Basic parameters of a light truck

表1. 某款轻型货车整车基本参数

3.1. MATLAB/Simulink爬坡度计算建模

根据上述汽车爬坡能力的理论基础，在MATLAB/Simulink平台上搭建出如图1所示的爬坡度计算仿真模型。该爬坡度计算模型由四个子系统组成，分别为驱动力计算子系统、空气阻力计算子系统、滚动阻力子系统、爬坡度计算子系统。

驱动力子系统由式(1)、(2)、(3)、(4)建立，其中主要运用了“Fcn模块”来完成计算模型的搭建，还利用“Saturation模块”，对汽车的转速进行了限制，以符合设定要求。最终以仿真车速为输入，实现对汽车的驱动力F_t的输出，汽车的驱动力计算子系统框图如图2所示。

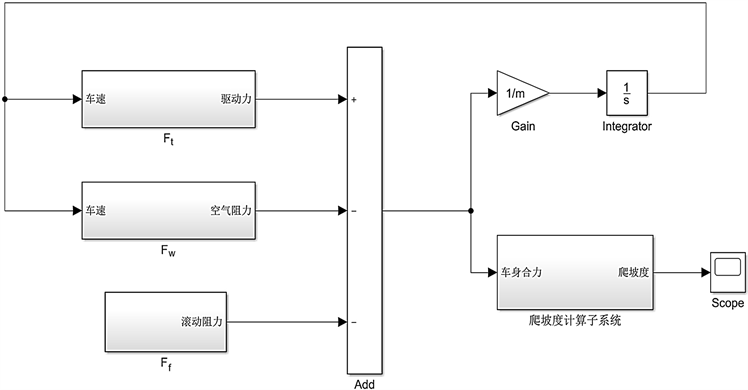
Figure 1. Simulation model of climbing degree calculation

图1. 爬坡度计算仿真模型

Figure 2. Block diagram of driving force subsystem

图2. 驱动力子系统框图

空气阻力子系统由式(5)、(6)建立，其中运用“In模块”，“Fcn模块”“Out模块”搭建，以仿真车速为输入，实现对空气阻力F_w的输出，空气阻力F_w子系统框图如图3所示。

Figure 3. Block diagram of air resistance subsystem

图3. 空气阻力子系统框图

滚动阻力子系统由式(7)建立，运用“Constant模块”对滚动阻力进行定义，实现对滚动阻力F_f的输出，滚动阻力F_f子系统框图如图4所示。

Figure 4. Block diagram of rolling resistance subsystem

图4. 滚动阻力子系统框图

爬坡度子系统由式(8)建立，根据公式选用“Gain模块”，“Trigonometric Function模块”搭建计算模型，对爬坡度进行运算，实现对爬坡度的输出，爬坡度子系统框图如图5所示。

Figure 5. Block diagram of climbing degree subsystem

图5. 爬坡度子系统框图

3.2. MATLAB App Designer程序界面设计

App Designer是MATLAB R2016A中正式推出的产品，旨在帮助用户利用新的图形系统且方便地设计更为美观的GUI (Graphical User Interface，图形用户界面) [4]。用户可利用App Designer对程序界面编辑设计，并对其行为功能进行编写，开发出专业的应用程序。

程序需根据某款轻型货车的整车参数和性能指标，实现爬坡能力参数匹配，故所设计的程序界面应具备多个“Edit Field”组件，供用户输入基本参数及显示数据结果；添加“UI Figure”组件，实现了爬坡度仿真曲线的绘制；“Button”组件的运用，用于命令匹配计算的开始。通过编辑和美化界面，设计出的程序界面如图6所示。

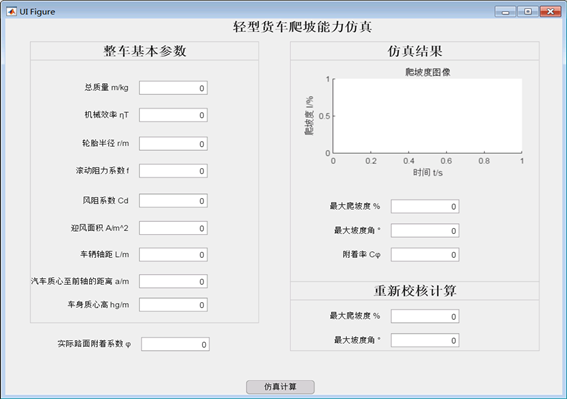
Figure 6. The designed program interface

图6. 设计的程序界面

程序界面的设计主要分为三个面板，左侧为“整车基本参数”面板，在该面板内可输入用于计算的参数；右侧为“仿真结果”及“重新校核计算”面板，该部分可展现爬坡度仿真曲线并显示爬坡能力相关参数计算结果。

3.3. MATLAB App Designer程序代码编写

所设计程序的代码，可在App Designer的代码视图中，对其功能代码进行编写。该程序可根据输入的整车基本参数和性能指标，通过点击“仿真计算”按钮计算爬坡能力相关数据，并在界面上绘制仿真图像，基于此功能的实现，编写的部分代码如图7所示。主要通过“sim”函数，使“Simulink”空间与“App Designer”空间实现了数据交互，程序可调用Simulink模型仿真得出的结果数据，在程序界面的仿真结果面板中绘制出爬坡度仿真曲线。借助“if”语句，检验计算出的附着率是否符合要求，并在“重新校核计算”面板中，得到最终确定的能满足实际路面附着系数的最大爬坡度和最大爬坡角。

Figure 7. Part of program code

图7. 部分程序代码

3.4. App Designer程序运行及参数匹配结果

经过调试，程序可顺利运行。在输入相应参数后，点击“仿真计算”按钮，可得到仿真图像及计算结果，图8为程序的运行结果。

Figure 8. Program running results

图8. 程序运行结果

从爬坡度图像中可以看出，货车爬坡度在0 s到1.7 s之间稳定在20%，之后逐渐上升，3.6 s时爬坡度到达最大，最后逐渐下降，最终稳定在28%左右。根据理论基础，校核计算得出该轻型货车的爬坡能力参数如表2所示。开发设计中，可根据参数匹配确定的最大爬坡度对所设计车辆的性能进行初步验证。

Table 2. Climbing ability parameter

表2. 爬坡能力参数

4. 结束语

本文基于MATLAB App Designer设计开发了一款汽车爬坡能力建模与仿真App，实现了与MATLAB/Simulink仿真数据的交互，在程序界面中绘制出了仿真图像并对爬坡能力相关参数进行了匹配计算。该款App的开发，也为汽车爬坡能力的确定，提供了一款简便实用的工具。

基金项目

自治区级大学生创新创业训练计划项目(项目名称：基于MATLAB的电动汽车关键技术的APP设计(201910593143)。