用户异质下铁路交通通勤者出行成本

The Travel Cost of Rail Commuters under Heterogeneous Users

摘要: 在铁路交通出行系统中，首先在考虑出发时间选择的基础上，通勤者按照早到惩罚与体触拥挤参数的差异被分成两组，研究了两组通勤者乘坐地铁时的出行行为，并由此推导出两组异质性用户乘坐铁路时的出行成本。其次，研究了双站点下两组异质性用户的出行行为，并由此推导出双站点下异质性用户乘坐铁路时的出行成本。研究表明，在考虑异质性差异的存在时，通勤者的出行成本相比同质性假设下的出行成本更低，且异质性差异越大成本将会越低，并且随着通勤人数的增长，异质性因素对出行成本的影响也将变得更显著。最后，算例的结果也表明了在进行铁路出行成本计算时，异质性因素需要被关注。

Abstract: In the railway transportation system, first of all, on the basis of considering the choice of departure time, commuters are divided into two groups according to the difference in the parameters of early arrival penalty and physical contact congestion. The travel behavior of the two groups of commuters when riding the subway is studied. This derives the travel costs of two groups of heterogeneous users when riding the railway. Secondly, the travel behavior of two groups of heterogeneous users under dual-sites is studied, and the travel costs of heterogeneous users under dual-sites are derived from this. Studies have shown that when considering the existence of heterogeneous differences, the travel cost of commuters is lower than the travel cost under the homogeneity assumption, and the greater the heterogeneity, the lower the cost, and as the number of commuters increases growth, the impact of heterogeneous factors on travel costs will also become more significant. Finally, the results of the calculation example also show that the heterogeneity factors need to be paid attention to when calculating the railway travel cost.

1. 引言

随着社会经济水平不断提高和基础建设的不断发展，出行方式也逐渐多样化，相应的出行行为研究也在逐步跟进。对于公路通勤者出行，Vickrey [1] 于1969年应用确定性排队理论，首次提出了瓶颈模型，即通过选择出发时间使得所有出行者具有相同出行成本的模型。随后，很多学者在此之上进行了一系列拓展。Arnott [2] [3] 等研究了用户异质对公路通勤者出行成本的影响。Liu和Nie [4] 研究了双瓶颈系统的出行问题。Huang [5] 则研究了考虑弹性需求的出行问题等。显然对于公路通勤出行而言，近年来的研究已经有了相当大的进展。

然而城市交通系统中不仅仅只有公路运输模式，还存在铁路等公共交通运输模式。公共交通的基本经济模式是Mohring [6] 于1972年提出的，其假设不存在拥堵，列车容量有限，用户随机到达车站。Kraus和Yoshida [7] 改进了公共交通模型，假设通勤者在车站排队等待乘车服务，每个乘车服务之间存在一个间隔。而Tabuchi [8] 在研究公路出行成本的基础上，还提出了一个与公路并行的铁路线路出行成本模型，其同样假设列车服务可以使通勤者准时到达且不存在拥堵。然而，他们提出的交通模型都类似于瓶颈模型，地铁交通需要一个与公路运输有所不同的出行成本表达。

随后，在Tabuchi [8] 的研究基础上，Danielis和Marcucci [9] 认为地铁交通虽然可以让人们准时到达工作地点，但车站及车厢内的体触拥挤也会给通勤者带来不适。Horowitz和Sheth [10] 认为如果这种拥挤很强烈的话还会导致通勤者认为自己失去独立性和隐私。Huang [11] [12] 则因此将体触拥挤成本引入地铁交通成本中，并且给出了可能的地铁交通成本表达。Rouwendal和Verhoef [13] 以及Buyukeren和Hiramatsu [14] 也采用了体触拥挤成本来进行出行成本研究。此外，在现实生活中，无论是收入水平还是个人偏好来看，出行者的时间价值并不相同，理想化的同质假设不能准确的描述出行者的出发选择行为。因此，除了体触拥挤成本之外，地铁交通异质性用户出行的研究也被学者所重视。Huang [11] 同时也研究了铁路交通通勤者的异质性情况，扩展了上述研究，但其使用的是静态模型。Van den Berg和Verhoef [15] 则研究了在动态发车下，异质性对用户出行的铁路交通成本影响。然而，高峰期过于严重的交通拥挤不仅会产生拥挤成本，还将导致出行者改变出发时间以避免拥挤。因此，Wu和Huang [16] 在计算铁路交通成本中考虑了出发时间选择，但却又忽视了异质性通勤者可能产生的影响。

本文首先在Wu和Huang [16] 等人的研究基础上，结合考虑出发时间选择和异质性因素，导出用户异质下的铁路交通成本表达，然后研究了多站点下异质性用户的出行行为及其成本表达，进而分析用户异质性对铁路交通通勤者出发时间选择和出行成本的影响。

2. 同质性用户铁路出行模型

考虑一个只含单一O-D对的简单交通网络，O (住宅区)和D (工作区)之间由一条铁路交通线路连接。每天早晨都会有N位通勤者乘坐该条地铁交通路线从O到达D处上班，并且每位通勤者的期望到达时间一致，为 $t^{*}$。我们假设铁路交通能力无限，可以让通勤者选择相同的出发时间准时到达工作，但同时也会给人们带来因车站和车厢内体触拥挤而产生的不适。这种不适感将会影响用户的出发时间选择，导致某些通勤者可能会选择提早或晚些出发，以避免体触拥挤。因此，我们需要考虑地铁交通通勤时间延误的惩罚成本，t时刻时的通勤者离开率越高，拥挤效应就越严重。令 $\alpha$， $\beta$， $\gamma$ 分别为铁路交通单位行驶时间成本、单位早到时间成本和单位晚到时间成本，假设 $0<\beta <\alpha <\gamma$ (根据Small [17] 的估计)，铁路交通通勤者的单位晚到时间成本和单位早到时间成本之比恒为常数，即 $\eta =\gamma /\beta$。

令 $r\left(t\right)$ 为铁路交通线路上的通勤者的离开率， $\left[t_s,t_e\right]$ 为铁路交通线路上通勤者选择的出行峰期，显然有 $r\left(t\right)=0,\forall t\notin \left[t_s,t_e\right]$。假设 $\xi$ 为在 $\left[t_s,t_e\right]$ 期间调度列车的时间间隔，且在本文中，为了便于研究通勤行为，我们遵循Wu和Huang [16] 中的假设，即在一个列车调度间隔期间，铁路交通线路通勤者的离开率是连续的，并且在一个时间间隔内的出发速率基本保持不变，也就是说，搭乘在 $t_0$ 时刻开出的列车的

乘客数目为 ${\displaystyle {\int }_{t_0-\xi }^{t_0}r\left(t\right)\text{d}t}\approx \xi t_0$。此外，假设铁路交通内部拥堵成本与车厢内乘客人数和行驶时间成正比。

因此，每个列车通勤者的出行成本由以下式子给出：

$C\left(t\right)=\{\begin{array}{l}\alpha T+\beta \left(\tilde{t}-t\right)+\psi \xi Tr\left(t\right)+F,t\in \left[t_s,\tilde{t}\right]\\ \alpha T+\gamma \left(\tilde{t}-t\right)+\psi \xi Tr\left(t\right)+F,t\in \left[\tilde{t},t_e\right]\end{array}$ (1)

其中， $\psi$ 为车厢拥挤参数，T为铁路自由流时间， $\psi \xi Tr\left(t\right)$ 为车厢内拥挤成本，F为铁路交通固定费用， $\tilde{t}$ 是铁路乘客可以准时到达自己的期望到达时间 $t^{*}$ 的出发时间，也即 $\tilde{t}+T=t^{*}$。在均衡情况下，任何一位通勤者都无法通过改变自己的出发时间来降低其出行成本。

在出行发生的最初时刻和出行结束的最末时刻，显然有 $r\left(t_s\right)=r\left(t_e\right)=0$，且在用户均衡情况下， $C\left(t_s\right)=C\left(t_e\right)=C\left(t\right),\forall t\in \left[t_s,t_e\right]$，即：

$C=\alpha T+\beta \left(\tilde{t}-t_s\right)+F=\alpha T+\gamma \left(t_e-\tilde{t}\right)+F$ (2)

将等式(2)代入等式(1)之中，在均衡的情况下，如图1所示，可得铁路交通通勤者离开率为：

$r\left(t\right)=\{\begin{array}{l}\frac{\beta \left(t-t_s\right)}{\psi \xi T},t\in \left[t_s,\tilde{t}\right]\\ \frac{\gamma \left(t_e-t\right)}{\psi \xi T},t\in \left[\tilde{t},t_e\right]\end{array}$ (3)

根据人数约束有 ${\displaystyle {\int }_{t_s}^{t_e}r\left(t\right)\text{d}t}=N$，并将等式(3)代入，可得：

$\beta {\left(t-t_s\right)}^2+\gamma {\left(t_e-t\right)}^2=2\psi \xi TN$ (4)

根据 $r\left(t_s\right)=r\left(t_e\right)=0$ 可得：

$\gamma \left(t_e-\tilde{t}\right)=\beta \left(\tilde{t}-t_s\right)$ (5)

整合等式(4)、(5)，以及 $t_s<t_e$，可得唯一合理解：

$t_s=\tilde{t}-\sqrt{2\delta \psi \xi TN}/\beta$ (6)

$t_e=\tilde{t}+\sqrt{2\delta \psi \xi TN}/\gamma$ (7)

其中， $\delta =\beta \gamma /\left(\beta +\gamma \right)$。

因此，将等式(6)代入等式(2)中，可得用户出行成本为：

$C=\alpha T+\sqrt{2\delta \psi \xi TN}+F$ (8)

Figure 1. Homogeneous railway commuter departure rate

图1. 同质性铁路通勤者离开率

3. 考虑出发时间下的异质性用户出行模型

3.1. 单站点异质性用户铁路交通出行成本

考虑存在两组异质性通勤者，也即 $i=1,2$。因为铁路交通到达准时有保障，列车并不会遇到排队等待状况，故而T为常量，所以异质性通勤者 ${\alpha }_i$ 的不同对分析结果没有影响，因此假设对于任意i，有 $\alpha \equiv {\alpha }_i$，但是允许 $\beta$， $\gamma$ 和 $\psi$ 随着通勤者不同而变化。令 ${\mu }_i={\beta }_i/{\psi }_i$， ${\gamma }_i/{\psi }_i=\left({\gamma }_i/{\beta }_i\right)\ast \left({\beta }_i/{\psi }_i\right)=\eta {\mu }_i$，为不失一般性，定义 $a=u_1/u_2\ge 1$ 为异质性差异，即第一组通勤者相对更注重早到带来的损失，而第二组通勤者则相对更注重体触拥挤带来的损失。又因为在拥挤峰期内，通勤者的离开率是连续的，所以根据Arnott [3] 中考虑公路异质性时的均衡，可以得到两组铁路交通通勤者均衡出发态如图2所示，由图可知第二组通勤者是早到期间( $\left[t_s,\tilde{t}\right]$ )最早出发的或者是在晚到期间( $\left[\tilde{t},t_e\right]$ )最迟出发的通勤者，因为在这两个时间段拥有着最低的相对体触拥挤成本。同样的，第一组通勤者则是选择在早到期间( $\left[t_s,\tilde{t}\right]$ )最迟出发或者在晚到期间( $\left[\tilde{t},t_e\right]$ )最早出发，因为在这两个时间段拥有着最低的相对延误成本。

Figure 2. Departure rate of railway commuters for heterogeneous users of single station

图2. 单站点异质性用户铁路通勤者离开率

如图2所示，显然，对于在 $\left[t_s,t_1\right]$ 期间出发的第二组通勤者而言，晚于 $t_1$ 时刻出发意味着面临着相对更高的通勤者离开率，这将导致付出的出行成本更高。同样的，对于在 $\left[t_1,\tilde{t}\right]$ 期间出发的第一组通勤者而言，早于 $t_1$ 时刻出发也意味着面临着相对更高的通勤者离开率，这将导致付出的出行成本更高，也即图2中的离开率曲线为等成本离开率曲线。而对于晚到期间的两组用户也是亦然。因此，与等式(1)相同，两组通勤者的成本分别由以下两式给出：

$C_1\left(t\right)=\{\begin{array}{l}\alpha T+{\beta }_1\left(\tilde{t}-t\right)+{\psi }_1\xi T{r}_1\left(t\right)+F,t\in \left[t_1,\tilde{t}\right]\\ \alpha T+{\gamma }_1\left(t-\tilde{t}\right)+{\psi }_1\xi T{r}_1\left(t\right)+F,t\in \left[\tilde{t},t_2\right]\end{array}$ (9)

$C_2\left(t\right)=\{\begin{array}{l}\alpha T+{\beta }_2\left(\tilde{t}-t\right)+{\psi }_2\xi T{r}_2\left(t\right)+F,t\in \left[t_s,t_1\right]\\ \alpha T+{\gamma }_2\left(t-\tilde{t}\right)+{\psi }_2\xi T{r}_2\left(t\right)+F,t\in \left[t_2,t_e\right]\end{array}$ (10)

与同质性通勤者出行情况相同，对于第二组通勤者，显然有 $r_2\left(t_s\right)=r_2\left(t_e\right)=0$，且在用户均衡情况下， $C_2\left(t_s\right)=C_2\left(t_e\right)=C_2\left(t\right),t\in \left[t_s,t_1\right]\cup \left[t_2,t_e\right]$，即：

$C_2=\alpha T+{\beta }_2\left(\tilde{t}-t_s\right)+F=\alpha T+{\gamma }_2\left(t_e-\tilde{t}\right)+F$ (11)

因此，在均衡的情况下，将等式(11)代入等式(10)，可得第二组通勤者的离开率为：

$r_2\left(t\right)=\{\begin{array}{l}\frac{{\mu }_2\left(t-t_s\right)}{\xi T},t\in \left[t_s,t_1\right]\\ \frac{\eta {\mu }_2\left(t_e-t\right)}{\xi T},t\in \left[t_2,t_e\right]\end{array}$ (12)

而对于第一组通勤者，在用户均衡情况下则有 $C_1\left(t_1\right)=C_1\left(t_2\right)=C_1\left(t\right),\forall t\in \left[t_1,t_2\right]$，即：

$C_1=\alpha T+{\beta }_1\left(\tilde{t}-t_1\right)+{\psi }_1\xi T{r}_1\left(t_1\right)+F=\alpha T+{\gamma }_1\left(\tilde{t}-t_2\right)+{\psi }_1\xi T{r}_1\left(t_2\right)+F$ (13)

由图2可知， $r_1\left(t_1\right)=r_2\left(t_1\right),r_1\left(t_2\right)=r_2\left(t_2\right)$，将等式(13)代入等式(9)中，可得第一组通勤者的离开率为：

$r_1\left(t\right)=\{\begin{array}{l}{r}_2\left(t_1\right)+\frac{{\mu }_1\left(t-t_1\right)}{\xi T},t\in \left[t_1,\tilde{t}\right]\\ r_2\left(t_2\right)+\frac{\eta {\mu }_1\left(t_2-t\right)}{\xi T},t\in \left[\tilde{t},t_2\right]\end{array}$ (14)

设第一组通勤者在通勤时总人数为 $N_1$，第二组用户数在通勤时总人数为 $N_2$， $N_1+N_2=N$，根据两组通勤者人数约束则有：

${\displaystyle {\int }_{t_1}^{\tilde{t}}{r}_1\left(t\right)\text{d}t}+{\displaystyle {\int }_{\tilde{t}}^{t_2}{r}_1\left(t\right)\text{d}t}=N_1$， (15)

${\displaystyle {\int }_{t_s}^{t_1}{r}_2\left(t\right)\text{d}t}+{\displaystyle {\int }_{t_2}^{t_e}{r}_2\left(t\right)\text{d}t}=N_2$， (16)

整合等式(11)~(16)，并且考虑时间顺序 $t_s<t_1<t_2<t_e$，可得唯一合理解：

$t_s=\tilde{t}-\left(\frac{\sqrt{a{N}_1+N_2}+\left(a-1\right)\sqrt{N_2}}{a}\right)\sqrt{2m\xi T/u_2}$， (17)

$t_1=\tilde{t}-\left(\frac{\sqrt{a{N}_1+N_2}-\sqrt{N_2}}{a}\right)\sqrt{2m\xi T/u_2}$， (18)

$t_2=\tilde{t}+\left(\frac{\sqrt{a{N}_1+N_2}-\sqrt{N_2}}{a}\right)\sqrt{2p\xi T/u_2}$， (19)

$t_e=\tilde{t}+\left(\frac{\sqrt{a{N}_1+N_2}+\left(a-1\right)\sqrt{N_2}}{a}\right)\sqrt{2p\xi T/u_2}$， (20)

其中， $m=\frac{\eta }{1+\eta }$， $p=\frac{1}{\eta \left(1+\eta \right)}$。

最后，将等式(17)代入等式(11)，可得第二组通勤者出行成本为：

$C_2=\alpha T+{\beta }_2\left(\frac{\sqrt{a{N}_1+N_2}+\left(a-1\right)\sqrt{N_2}}{a}\right)\sqrt{2m\xi T/u_2}+F$， (21)

同时，也可得第一组通勤者出行成本为：

$C_1=\alpha T+{\beta }_1\sqrt{\frac{a{N}_1+N_2}{a}}\sqrt{2m\xi T/u_1}+F$， (22)

从等式(22)可知，当 ${\beta }_1={\beta }_2,a=u_1/u_2=1$ 时，即两组用户同质时，等式(21)与等式(22)相同且化为同质性情况下的出行成本。

进一步地，考虑G组通勤者，且他们之间的关系为 ${\mu }_1\ge {\mu }_2\ge \cdots \ge {\mu }_G$，并令 $N_i$ 为第i组的通勤者数，N为总通勤者数。同样的，在用户均衡时，每一组组通勤者的离开率的斜率均为 ${\mu }_i\left(t-t_s\right)/\left(\xi T\right),t\in \left[t_j,t_i\right]$ 和 $\eta {\mu }_i\left(t_e-t\right)/\left(\xi T\right),t\in \left[{t^{\prime }}_i,{t^{\prime }}_j\right]$。以五组通勤者为例，则铁路交通通勤者离开率应为如下图3所示：

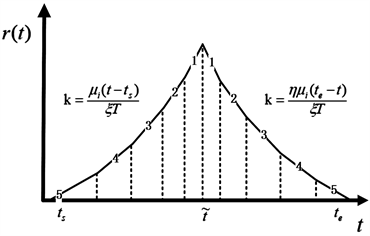
Figure 3. Departure rate of railway commuters in five groups for heterogeneous users

图3. 五组异质性用户铁路通勤者离开率

图3显示了五个组的平衡示例。第五组通勤者出行时间相对成本最低，在高峰时间开始和结束时出发。第四组在相邻的时间间隔上旅行，以此类推。显然可以推知，当G趋于无穷时，铁路交通通勤者离开率将变为一条光滑的曲线。

3.2. 双站点异质性用户铁路交通出行成本

考虑一个只含两个铁路站点生活区O₁和O₂以及一个工作区D的简单交通网络，住宅区和工作区之间由一条铁路交通线路连接，如图4所示。两组居民居住在O₁和O₂两个生活区，并且从O₁乘车至O₂以及从O₂乘车至D之间的时间都为T，对体触拥挤更为厌恶的第二组通勤者居住在O₂处，第一组通勤者则居住在远离市中心的O₁处，也即 ${\mu }_1\ge {\mu }_2$。

Figure 4. Dual-site transportation network

图4. 双站点交通网络

此时，因为 ${\mu }_1\ge {\mu }_2$，且第二组通勤者居住区更近于工作区，则可假设其最早出发时间 $t_s+T\ge {t^{\prime }}_s$ 且 $t_e+T\le {t^{\prime }}_e$。则两组通勤者的成本分别由以下两式给出：

$C_1\left(t\right)=\{\begin{array}{l}2\alpha T+{\beta }_1\left(\tilde{t}-t\right)+{\psi }_1\xi T{r}_1\left(t\right)+{\psi }_1\xi T\left[r_1\left(t\right)+r_2\left(t+T\right)\right]+F,t\in \left[t_s,\tilde{t}\right]\\ 2\alpha T+{\gamma }_1\left(t-\tilde{t}\right)+{\psi }_1\xi T{r}_1\left(t\right)+{\psi }_1\xi T\left[r_1\left(t\right)+r_2\left(t+T\right)\right]+F,t\in \left[\tilde{t},t_e\right]\end{array}$ (23)

$C_2\left(t\right)=\{\begin{array}{l}\alpha T+{\beta }_2\left(\tilde{t}+T-t\right)+{\psi }_2\xi T\left[r_1\left(t-T\right)+r_2\left(t\right)\right]+F,t\in \left[{t^{\prime }}_s,\tilde{t}+T\right]\\ \alpha T+{\gamma }_2\left(t-\tilde{t}-T\right)+{\psi }_2\xi T\left[r_1\left(t-T\right)+r_2\left(t\right)\right]+F,t\in \left[\tilde{t}+T,{t^{\prime }}_e\right]\end{array}$ (24)

同样的，在均衡情况下，求得两组通勤者的离开率如图5及下式所示：

$r_1\left(t\right)=\{\begin{array}{l}\frac{\left({\mu }_1-{\mu }_2\right)\left(t-t_s\right)}{\xi T},t\in \left[t_s,\tilde{t}\right]\\ \frac{\eta \left({\mu }_1-{\mu }_2\right)\left(t_e-t\right)}{\xi T},t\in \left[\tilde{t},t_e\right]\\ 0,其他\end{array}$ (25)

$r_2\left(t\right)=\{\begin{array}{l}\frac{{\mu }_2\left(t-{t^{\prime }}_s\right)}{\xi T}-r_1\left(t-T\right),t\in \left[{t^{\prime }}_s,\tilde{t}+T\right]\\ \frac{\eta {\mu }_2\left({t^{\prime }}_e-t\right)}{\xi T}-r_1\left(t-T\right),t\in \left[\tilde{t}+T,{t^{\prime }}_e\right]\end{array}$ (26)

Figure 5. Dual-site transportation network

图5. 双站点交通网络

设第一组通勤者在通勤时总人数为 $N_1$，第二组用户数在通勤时总人数为 $N_2$， $N_1+N_2=N$，根据均衡条件及两组通勤者人数约束，可得唯一合理解：

$t_s=\tilde{t}-\sqrt{2m\xi T{N}_1/\left(u_1-u_2\right)}$， (27)

$t_e=\tilde{t}+\sqrt{2p\xi T{N}_1/\left(u_1-u_2\right)}$， (28)

${t^{\prime }}_s=\tilde{t}-\sqrt{2m\xi TN/u_2}+T$， (29)

${t^{\prime }}_e=\tilde{t}+\sqrt{2p\xi TN/u_2}+T$， (30)

最后，代入等式可得两组通勤者出行成本分别为：

$C_1=2\alpha T+{\beta }_1\sqrt{2m\xi T{N}_1/\left(u_1-u_2\right)}+{\psi }_1\sqrt{2u_{2}m\xi TN}+F$， (31)

$C_2=\alpha T+{\beta }_2\sqrt{2m\xi TN/u_2}+F$。 (32)

可以看到，距离工作区更近的第二组通勤者，其通勤成本只受到通勤者总人数影响，而距离工作区更远的第一组通勤者的成本则还受到两组通勤者之间的异质性差异影响。

3.3. 模型性质

性质1：在用户均衡时，铁路出行中每一组通勤者中有 $\eta /\left(1+\eta \right)$ 的部分是提前出发的，其余则是延后出发。

证明：首先考虑最早出发的第一组通勤者，显然有 $r_1\left(t_s\right)=r_1\left(t_e\right)=0$，且在用户均衡情况下， $C_1\left(t_s\right)=C_1\left(t_e\right)=C_1\left(t\right),t\in \left[t_s,t_1\right]\cup \left[{t^{\prime }}_1,t_e\right]$，即：

$C_1=\alpha T+{\beta }_1\left(t_1-t_s\right)+F=\alpha T+{\gamma }_1\left(t_e-{t^{\prime }}_1\right)+F$ (33)

又因为该组通勤者中提前出发与延后出发的人数分别为 ${\displaystyle {\int }_{t_s}^{t_1}{r}_1\left(t\right)\text{d}t}$ 及 ${\displaystyle {\int }_{{t^{\prime }}_1}^{t_e}{r}_1\left(t\right)\text{d}t}$，将 $r_1\left(t\right)$ 以及等式(33)代入，即可证明该组通勤者中提前出发与延后出发的人数之比为 $\eta$，也即有 $\eta /\left(1+\eta \right)$ 的部分人数是提前出发，以此可类推至最后一组。

性质2：对单站点两组异质性通勤者，当某组通勤者本身的成本参数 $\alpha ,{\beta }_i,{\gamma }_i$ 和 ${\psi }_i$ 不变时，也即 $u_1$ 或 $u_2$ 不变，随着异质性差异a变大，该组通勤者出行成本将会减少。

证明：为简化证明，令 $N_1=N_2$，则 $C_2=\alpha T+{\beta }_2\left(\left(\sqrt{a+1}+a-1\right)/a\right)\sqrt{m\xi TN/u_2}+F$，当第二组通勤者的成本参数 $\alpha ,{\beta }_2,{\gamma }_2$ 和 ${\psi }_2$ 不变时， $\partial \left[\sqrt{a+1}+a-1\right]/\partial a\le 0$，也即 $\partial C_2\left(t\right)/\partial a\le 0$，这就意味着随着异质性差异a变大，该组通勤者出行成本将会逐渐下降，而当 $a\to +\infty$ 时， $\left(\sqrt{a+1}+a-1\right)/a\to 1$，其出行成本将与只有N/2位第二组通勤者乘坐地铁交通时所产生的出行成本相等。同样的，当第一组通勤者的成本参数 $\alpha ,{\beta }_1,{\gamma }_1$ 和 ${\psi }_1$ 不变时， $\partial \left[\sqrt{\left(a+1\right)/a}\right]/\partial a\le 0$，也即 $\partial C_1\left(t\right)/\partial a\le 0$，而当 $a\to +\infty$ 时， $\sqrt{\left(a+1\right)/a}\to 1$，其出行成本将与只有N/2位第一组通勤者乘坐地铁交通时所产生的出行成本相等。

性质3：对单站点两组异质性通勤者，当相对拥挤成本较大的第二组通勤者本身的成本参数 $\alpha ,{\beta }_2,{\gamma }_2$ 和 ${\psi }_2$ 不变时，随着异质性差异a变大，通勤峰期( $\left[t_e,t_s\right]$ 以及 $\left[t_1,t_2\right]$ )将会缩短。当相对拥挤成本较小的第一组通勤者本身的成本参数 $\alpha ,{\beta }_1,{\gamma }_1$ 和 ${\psi }_1$ 不变时，随着异质性差异a变大，通勤峰期( $\left[t_e,t_s\right]$ 以及 $\left[t_1,t_2\right]$ )将会增大。

证明：为简化证明，令 $N_1=N_2$，则 $t_e-t_s=\left(\left(\sqrt{a+1}+a-1\right)/a\right)\left(\sqrt{2p\xi TN/u_2}+\sqrt{2m\xi TN/u_2}，\right)$，以及 $t_2-t_1=\left(\left(\sqrt{a+1}-1\right)/a\right)\left(\sqrt{2p\xi TN/u_2}+\sqrt{2m\xi TN/u_2}\right)$，则当第二组通勤者本身的参数 $\alpha ,{\beta }_2,{\gamma }_2$ 和 ${\psi }_2$ 不变时， $\partial \left[\sqrt{a+1}+a-1\right]/\partial a\le 0$， $\partial \left[\sqrt{a+1}-1\right]/\partial a\le 0$ 也即 $\partial \left(t_e-t_s\right)/\partial a\le 0$， $\partial \left(t_2-t_1\right)/\partial a\le 0$，这就意味着随着异质性差异a变大，通勤峰期( $\left[t_e,t_s\right]$ 以及 $\left[t_1,t_2\right]$ )将会缩短。而同样的，当第一组通勤者本身的成本参数 $\alpha ,{\beta }_1,{\gamma }_1$ 和 ${\psi }_1$ 不变时， $\partial \left[\sqrt{\left(a+1\right)/a}\right]/\partial a\le 0$， $\partial \left[\left(\sqrt{a+1}-1\right)/\sqrt{a}\right]/\partial a\le 0$，也即 $\partial \left(t_e-t_s\right)/\partial a\ge 0$， $\partial \left(t_2-t_1\right)/\partial a\ge 0$，这就意味着随着异质性差异a变大，通勤峰期( $\left[t_e,t_s\right]$ 以及 $\left[t_1,t_2\right]$ )将会增大。

由性质1和性质2，我们可以看出，与同质性通勤者出行成本相比，考虑异质性因素的通勤者的出行成本将会更小，而随着异质性差异a增大，通勤者成本还会进一步减小。因为当 $u_2$ 不变时，a的增大，也即 $u_1$ 的增大意味着第一组通勤者越发重视早到带来的成本损失，这将会使得第一组通勤者相对忽略车厢内拥挤带来的损失，越发集中在 $\tilde{t}$ 时刻出发，这就使得 $\left[t_1,t_2\right]$ 缩短，从而 $\left[t_e,t_s\right]$ 也会缩短，也就让第二组通勤者相对更接近于 $\tilde{t}$ 时刻出发，减少了其延误成本损失。而当 $u_1$ 不变时的情况也类似。

4. 地铁出行数值分析

下面用单站点两组通勤者的数值算例进行验证上述结论。本文部分基本参数来源于Wu和Huang [16]，并进行了适当的调整。具体参数假设如下： $N=10000人$， $T=40分钟$， $F=6元$， $t^{*}=9:00\text{am}$， $N_1=N_2=N/2=5000人$， $\left(\alpha ,{\beta }_1,{\gamma }_1\right)=\left(1.2,0.6,3.0\right)\left(元/分钟\right)$， $\left(\alpha ,{\beta }_2,{\gamma }_2\right)=\left(1.2,0.5,2.5\right)\left(元/分钟\right)$， $\xi =2.5分钟$， ${\psi }_1=0.0003$， ${\psi }_2=0.0005$。

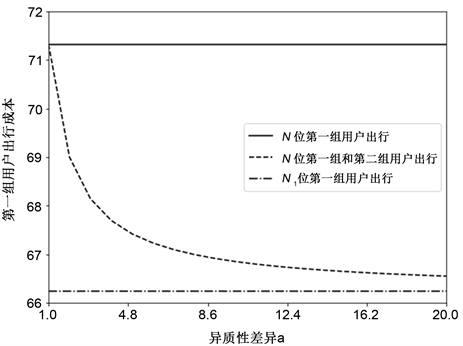
Figure 6. The first group of commuters travel cost change chart

图6. 第一组通勤者出行成本变化图

Figure 7. The second group of commuters travel cost change chart

图7. 第二组通勤者出行成本变化图

图6显示了三种情况下的第一组通勤者出行成本，显然，当异质性差异 $a=1$ 时，也即第一组和第二组通勤者之间不存在异质性差异时，相当于只有N位第一组通勤者乘坐地铁出行，也就是图6当中的实线所对应的出行成本，这里 $N_1+N_2=N$。而随着异质性差异a逐渐增大，两组通勤者出行差异逐渐增大，第一组通勤者出行成本将逐渐降低，而从图6中的虚线也可看出，而当异质性差异 $a\to +\infty$ 时，其出行成本将下降至相当于只有N₁位第一组通勤者乘坐地铁交通时所产生的出行成本。而从图7也是可以得出第二组通勤者在相似出行情况下的同一结论，并且这一结果也与Van den Berg和Verhoef [15] 的研究结果相一致。此外，对比图6和图7的横坐标，我们还可以看出相对重视延误损失的第一组通勤者对异质性差异a的变化更为敏感。

为了表述简洁，本文中把只有 $N$ 位第一组通勤者乘坐地铁交通的出行成本称为同质性下第一组用户出行成本，把 $N_1$ 位第一组通勤者和 $N_2$ 第二组通勤者联合出行时的第一组通勤者成本称为异质性下第一组用户出行成本，第二组用户出行成本也是类似定义。显然，从图8中我们可以看出，随着通勤人数 $N$ 从0增加15,000人，异质性下用户出行成本与同质性的用户出行成本之差将会逐步增大，当 $N$ = 5000人时，第一组和第二组的差异分别是 $0.7\%$ 和 $2.5\%$，而当 $N$ 增至15,000人时，第一组和第二组的差异上升至 $1.1\%$ 和 $3.9\%$。并且，从图6中我们还可以明显地看出，是否考虑异质性因素对第二组用户的出行成本计算影响不是很大，而对于相对重视延误损失的第一组用户，计算其出行成本时则不可随意忽略这一因素，这也正是由于两组通勤者对异质性差异 $a$ 变化的敏感程度不同所造成的。

Figure 8. The graph of travel costs with the number of commuters

图8. 出行成本随通勤者人数变化图

5. 研究结论

本文主要是研究了地铁交通通勤者在异质性假设下及双站点下的出行成本问题。异质性通勤者按照其单位早到成本与拥挤成本损失的比值递增的顺序，在早到期间依次出发，而在晚到期间则按照比值递减的顺序依次出发以便使自己的出行成本最小。然后，根据离开率、人数等约束条件导出各组通勤者的地铁交通出行成本表达。从所求得的单站点各组通勤者的地铁交通出行成本我们可以看出，随着异质性差异的增大，通勤者出行成本将会逐渐减小，通勤峰期也会随之改变。而对双站点通勤者出行模型来说，距离工作区更近的通勤者其通勤成本只受到通勤者总人数影响，而距离工作区更远的通勤者的成本则还受到通勤者之间的异质性差异影响。随后本文对单站点异质性出行进行了数值模拟，发现对于相对重视延误成本的通勤者来说，其对异质性差异变化并不敏感，而对于相对重视拥挤成本的通勤者来说，则不可随意忽略异质性因素对其成本计算产生的影响，并且随着通勤人数的增加这一因素将会对的出行成本计算产生更大的影响。

本论文在Wu和Huang [16] 等人的研究基础上，结合考虑出发时间选择和异质性因素，研究了用户异质下通勤者乘坐地铁交通时的出行成本，但还存在很多的问题值得下一步研究，例如连续异质性通勤者、拥挤收费下与公路异质性通勤者组合产生的出行选择问题等等。

参考文献