基于HUST-Ship的方波数值造波方法研究

Numerical Studies of Square Wave Generation Using HUST-Ship

摘要: 当不同的天气模式导致海洋在不同的方向产生两个海流系统时，就会产生一个交叉波，最终导致海面上的方波生成。方波的出现将威胁船舶的航行性能，严重时可能导致船舶倾覆。本文利用自研CFD软件HUST-Ship开展了基于规则波叠加方法进行方波数值波浪水池的研究。在进行数值模拟时，对不可压缩流体的RANS方程进行求解，数值造波采用在入口边界施加相应规则波的数学方程模拟方波，自由液面采用level-set方法获取。数值模拟结果表明两个有90度交叉角、相同波长和相位的规则波叠加在一起能够形成方波。选择水池中的四个点作为标记点，追踪标记点处液面高度变化，仿真结果与解析解得到的结果吻合。

Abstract: When two waves in different directions meet due to different weather patterns, a cross wave pattern will be generated, which will finally result in the spread of square waves on the sea surface. The emergence of square waves will threaten the navigation performance of the ship and may lead to ship capsized in severe case. In this paper, the numerical square wave flume is developed by using the in-house CFD software HUST-Ship. In the process of data simulation, by means of solving the RANS equation of incompressible fluid, the analytical solution of the corresponding regular wave is imposed at the inlet boundary, and the free surface is captured by level-set method. Two regular waves with a cross angle of 90 degrees and the same wavelength and phase are superimposed. The probe is used to deal with the simulation results and trace the selected points to obtain the relative errors between the simulation results and the analytical solutions. Moreover, error analysis is used to ensure the accuracy of the numerical tank.

1. 引言

随着海洋资源的开发利用，船舶航线由近海向远洋延伸已成为一种必然趋势。这一趋势意味着船舶更有可能遇到极端的海洋环境和不可预测的天气模式，因此复杂的海洋条件和天气模式的结合增加了遇到方波的风险。为了保证水面舰船的生命力和安全，有必要对方波进行分析。

方波的形成是两个方向的波浪在一定角度上相交而产生相互作用的一种海况。世界各国科学家对方波的形成机理、数值模拟的理论和方法以及波的特性进行了研究。关于交叉波的非线性动力学已有许多早期研究。2003年，Janssen等 [1] 利用Zakharov方程对系综系统进行了直接模拟，将齐次四波相互作用理论扩展到包括非共振传输效应，揭示了四波相互作用在表面重力波谱演化中的重要作用。在线性理论中，波之间没有相互作用。在线性理论中，波之间不存在相互作用。只有当波的相位有利时，波的能量才会叠加，最高可增加一倍。然而，非线性波的情况是不同的，因为波之间的相互作用。由于相互作用，波高最多可达一维平均波高的3倍，二维平均波高的4.5~5倍。他们验证了观察到的概率分布函数和理论概率分布函数之间有很好的一致性。Onorato等人 [2] 在2006年使用了一个简单的弱非线性模型来描述不同传播方向的双波系统的相互作用。假设两个海洋系统都是窄带状的，他们通过Zakharov方程两个耦合非线性薛定谔方程，描述每个波谱峰的演变过程。对于单个不稳定平面波，引入在不同方向传播的第二个平面波会导致不稳定增长速率的增加和不稳定区域的扩展。2011年，Toffoli等人 [3] 研究了过海条件下地表高程的统计特性。在波浪水池内进行了实验，采用高阶法求解欧拉方程得到了数值结果。用高阶谱法进行的数值模拟与实验结果吻合较好。数值和实验结果表明，极端事件的数量与两个相互作用的系统之间的角度有关。不稳定性可能是由共存的非共线波系之间的非线性相互作用引起的。2012年，Cavaleri等人 [4] 分析了Louis Majesty游轮遭遇巨浪袭击事故的海况。利用波浪模型(WAM)对局部波浪条件进行了详细的后推。结果表明，存在两个频率几乎相同的相似波系，并用两个耦合非线性薛定谔(CNLS)方程讨论了海况。2015年Trulsen等人 [5] 研究了油轮Prestige事故中极端海况和异常浪发生的概率。这两个波系几乎成直角相交。利用四种不同的非线性模型，他们能够估计大波出现的统计数据。在事故发生的那一刻，最大峰值高度比预期的峰值高度高出约5%~6%。两个交叉波系统之间可能存在非线性相互作用，但实际上不会改变峰度或最大峰高。Senthilkumar等人 [6] 使用HilbertHuang变换(HHT)讨论了方波海态的结果，它是经验模态分解(EMD)和希尔伯特谱分析(HSA)的结果。HHT采用HSA方法获取瞬时频率数据，EMD方法将信号分解为所谓的固有模态函数。2018年，Gramstad等 [7] 研究了波的统计特性和极端波的发生。该研究不仅涉及单个波系的光谱形状，而且涉及两个波系的交叉角和峰值频率的分离。利用Zakharo方程分析了两种交叉stokes波的调制不稳定性，该方程适用于任意带宽的扰动。峰度与两种Stokes波的最大不稳定生长速率呈正相关。2018年，Brennan [8] 等利用高阶谱方法求解自由表面欧拉方程，研究了方波海况的演化和该系统中巨浪的出现。分析了两种交叉波系统：一种是利用Draupner波在不同角度交叉的方向谱，另一种是利用Draupner波与窄带JONSWAP状态交叉的方向谱来模拟风胀与海之间的光谱增长。虽然交叉角对统计演化有一定影响，但三阶效应不显著。

本研究采用自研粘性流CFD软件研究方波的数值造波方法，形成了基于粘性流CFD的数值方波水池，分析了产生方波的相对误差，仿真结果和解析解的结果比较验证了仿真结果的可靠性。

2. 流体控制方程和数值方法

2.1. 控制方程

HUST-Ship采用有限差分法对URANS方程进行离散，采用水平集法对自由液面进行捕获。不可压缩连续方程和RANS方程如下：

$\frac{\partial u_i}{\partial x_i}=0$ (1)

$\frac{\partial \overline{u_i{u}_j}}{\partial x_j}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\gamma \left(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i}\right)\right]-\frac{\partial \left(-\overline{{u^{\prime }}_i{u^{\prime }}_j}\right)}{\partial x_j}+f_i$ (2)

其中： $\overline{u_i}$ 代表时均速度； ${u^{\prime }}_i$ 代表脉动速度； $\overline{{u^{\prime }}_i{u^{\prime }}_j}$ 代表雷诺应力；f_i表示体积力。

在基于粘性流体理论构建的数值波池中，自由表面处理方法采用level-set的方法进行处理。以水为自由界面，为流场中任意点到液体表面的距离函数， $\phi >0$ 表示空气， $\phi <0$ 表示水。在任意时刻自由表面为零，意味着液体表面上的任何点都为0 [9] [10]。

$\frac{\partial \phi }{\partial t}+v\nabla \phi =0$ (3)

其中v为流场中的速度矢量。

利用插值法求自由曲面，在方程的局部区域内求解流动液体。 $\phi <0$ 由单相水平集法得到：

$\nabla v\cdot n_j=0,n_j=\frac{\partial \phi /\partial x_i}{\left|\partial \phi /\partial x_i\right|}$ (4)

水平集方法的主要优点是网格质量稳定，易于控制。计算两个交点界面处的曲率和法向量更容易、更方便，模拟自由曲面的精度更高。

2.2. 造波与消波的方法

使用边界造波法实现造波(边界造波法是在入口处设置相应的水质点运动速度来实现造波的方法 [11] [12] )。通过在入口边界设置速度条件形成方波，其任意时刻的幅值可由幅值相同、波长相同、垂直相交方向相同的两个简谐波线性波叠加而成。

在模拟目标波时(与数值水池产生的普通单向波不同，本研究数值水池有两个入口)，流场入口自由表面位置设为余弦函数：

$\eta \left(t\right)=A\cos \left(kx-\omega t+\phi \right)$ (5)

流体质点在入口的速度设置为：

$u=A\omega \frac{\cosh k\left(z+d\right)}{\sinh kd}\sin \left(kx-\omega t+\phi \right)$ (6)

$w=A\omega \frac{\sinh k\left(z+d\right)}{\sinh kd}\sin \left(kx-\omega t+\phi \right)$ (7)

其中A为幅值；d为水深；k是波数；Ox为波传播方向，Oy为水池宽方向，Oz为水深方向；u是ox方向上的速度，w是oz方向上的速度，z = 0是静态水面。

方波仿真过程中采用了网格衰减和阻尼消波两种方法。网格衰减是一种简单实用的方法，通过设置逐渐粗化的网格或在水池末端附加一个扩展区域，使其数值耗散。与均匀网格相比，该方法可以减少计算量。

数值波水池的阻尼消波方法修正了消波区动量方程。修正的动量方程为：

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=g_x-\frac{1}{\rho }\frac{\partial p}{\partial x}+v\left[\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right]-\mu \left(x\right)u$ (8)

$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=g_y-\frac{1}{\rho }\frac{\partial p}{\partial y}+v\left[\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right]-\mu \left(x\right)v$ (9)

式中，为人工阻尼系数，其大小在消波区沿波传播方向为线性阻尼：

$\mu \left(x\right)=\{\begin{array}{l}{a}_s\left(x-x_0\right)/L_{s}x>x_0\\ 0x\le x_0\end{array}$ (10)

$x_0$ 为消波开始起作用的位置； $L_s$ 为阻尼层总长度； $a_s$ 为消波的强度。消波强度是一个经验值。值越大，消波强度越大。但是，如果这个值太大，可能会产生负面影响，导致更严重的反射波。因此，有必要选择一个合理的消波强度值，以获得更好的模拟结果。

3. 数值波浪水池

建立单位长度7、宽度7、高1.4 (自由液面上方)、水池深度1的数值造波计算域，如图1所示。水池前部是一个足够大的造波浪的区域，其俯视图为边长4的正方形。如果今后开展方波的耐波性研究，在数值模拟过程中真实船舶的长度将被缩放到1，产生波区域的大小可以完全满足要求。水池的后端是出口附近的波吸收区域(波吸收区域的长度是3米)，而消波强度是设置为1，这是用于提高质量的模拟波结合网格的耗散效应。在网格生成方面，产生波区域沿x轴和y轴采用均匀网格布局，消波区域网格逐渐粗化。对自由液面附近的网格分布进行加密，可以准确地模拟波面变化。该加密区域布置在一个自由均匀的网格中，且远离波面的上下方向较粗。

数值水池的边界条件如图2所示。数值水池的前端为入口边界条件(inlet)；出口为零压力边界条件(Farfield#1)，共有两个出口和两个入口。底部为零压力边界条件(Farfield#1)；顶部为零压力梯度(Farfield#2)的边界条件。网格边界层离壁面的距离均满足y+ = 1，雷诺数Re = 4.545E6，弗劳德数Fr = 0.168，压力-速度耦合采用标准投影算法。网格点分布如图3所示。

4. 方波数值造波和误差分析

方波仿真结果如图4所示。从造波区可以看出，波面呈方形(波高为0.02)，与预期结果一致。根据Airy波原理，将方波的解析解由两个方向正交的规则波叠加，得到的解析解的波形如图5所示，其数学表达式如下：

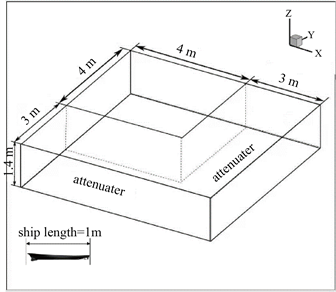
Figure 1. Dimension of the computation domain

图1. 计算域几何尺寸示意图

Figure 2. Boundary condition

图2. 数值模型的边界条件

Figure 3. Grid distribution

图3. 型网格点分布

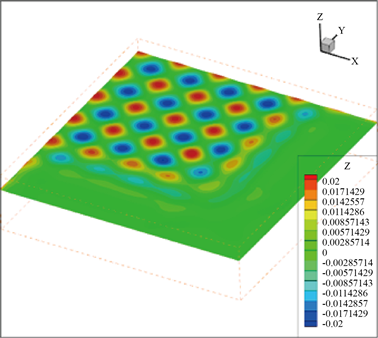
Figure 4. Numerical results of square wave

图4. 方波的波形模拟结果

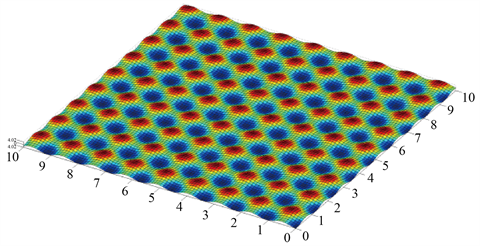
Figure 5. Analytical results of square wave

图5. 方波的解析解结果

$x=0.02\cos \left(5.461x-13.884t\right)+0.02\left(-5.461y-13.884t\right)$ (11)

与常规波水池不同，方波水池内各点的最大幅值并不完全相同，其最大幅值由该点相交波的叠加确定。为了评价数值波的精度，通过追踪选定点的液面高度随时间变化特性，比较最大幅值时域特性的相对误差及其连续变化，来验证数值造波的精度。在数值模拟过程中，为避免造波区到消波区过程的影响，对远离消波区的造波区域的波形特性进行分析和研究。通过选取造波区域中心的4个不同位置的点作为监测点，如图6所示，得到这4个监测点幅值的时域曲线。

将仿真结果与解析解进行了比较，得到了相对误差时历曲线。点1的幅值解析解最大为0.020，将仿真结果与解析解进行比较，如图7所示，相对误差如图8所示。监测点1的幅值误差均小于5%。

监测点点2的幅值解析解最大为0.018，将仿真结果与解析解进行对比，如图9所示，相对误差如图10所示。从相对误差的图可以看出，监测点2的幅值误差均小于4%。

点3处的幅值解析解最大为0.018，将仿真结果的时域特性与解析解进行比较，如图11所示。相对误差如图12所示。从相对误差的图可以看出，监测点2的幅值误差均小于5%。

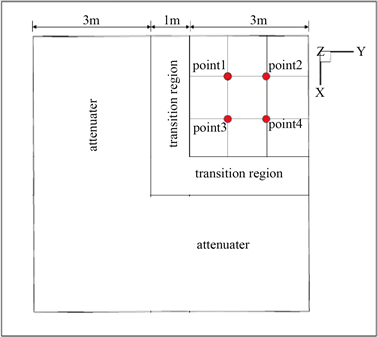
Figure 6. Monitor points of wave amplitudes in computational domain

图6. 监测点布置图

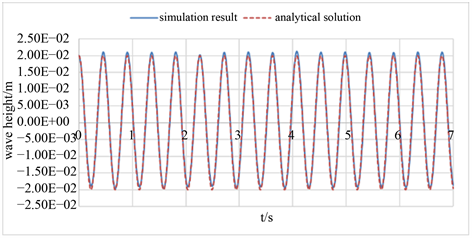
Figure 7. Comparison of wave amplitude between numerical and analytical results at point 1

图7. 监测点1的仿真结果与解析解比较

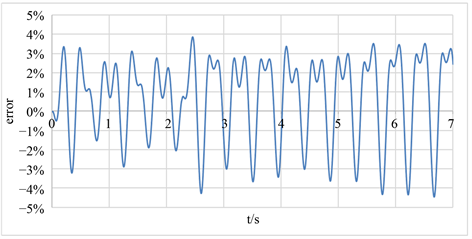
Figure 8. Comparison of wave amplitude difference between numerical and analytical results at point 1

图8. 监测点1最大幅值的相对误差

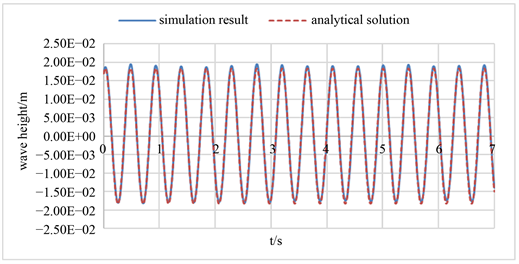
Figure 9. Comparison of wave amplitude between numerical and analytical results at point 2

图9. 监测点2的仿真结果与解析解比较

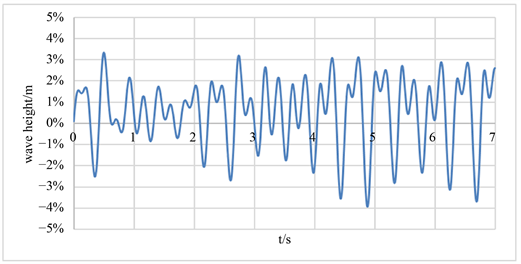
Figure 10. Comparison of wave amplitude difference between numerical and analytical results at point 2

图10. 监测点2最大幅值的相对误差

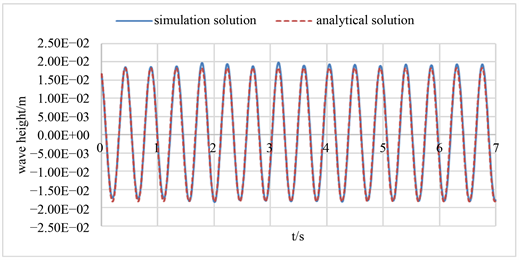
Figure 11. Comparison of wave amplitude between numerical and analytical results at point 3

图11. 仿真结果与点3的解析解

点4的最大幅值解析解为0.014，将仿真结果与解析解进行比较，如图13所示。相对误差如图14所示。

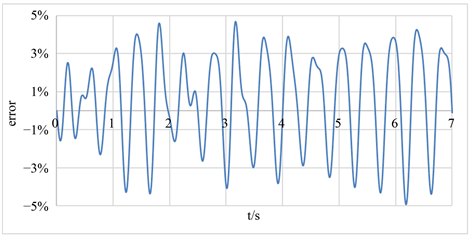
Figure 12. Comparison of wave amplitude difference between numerical and analytical results at point 3

图12. 点3最大幅值的相对误差

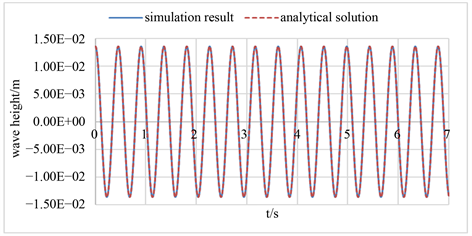
Figure 13. Comparison of wave amplitude between numerical and analytical results at point 4

图13. 仿真结果与点4的解析解

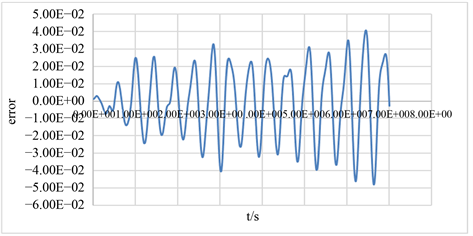
Figure 14. Comparison of wave amplitude difference between numerical and analytical results at point 4

图14. 点4最大幅值的相对误差

5. 结论

本文利用自研的粘性流CFD软件HUST-Ship，使用在边界输入速度条件的边界造波法，通过两个相位相同方向90度相交的规则波进行叠加生成方波，采用level-set方法捕获自由液面的运动。根据规则波的叠加理论，得到了两个相位相同方向90度相交的规则波进行叠加后波浪的解析解。对基于粘性流CFD软件得到方波进行了分析，采用双入口数值水池，使用边界造波法，即可得到对应的方波。通过比较监测点时域特性的运动幅值相对误差。对采用粘性流CFD软件的方波的造波精度进行了评估，仿真结果与解析解吻合较好，方波幅值与解析解比较相对误差小于5%，采用上述方法得到的数值方波能够用于分析和研究方波对舰船航行性能的评估和预报，为后期分析和研究方波对船舶航行安全性影响奠定了坚实的基础。