材料力学中梁内单根纵向纤维弯曲变形研究

The Bending Deformation Analysis of a Beam Longitudinal Fiber in Mechanics of Materials

摘要: 众所周知，根据单向受力假设，在纯弯矩作用下只在梁横截面上存在正应力，而不存在横向正应力。因此，可能会出现这样的疑问:对于梁上横向尺寸趋于零的纵向纤维，在这样的应力状态下为何会发生弯曲？本文将简要讨论这个问题。首先，梁中任意薄层的弯曲应力梯度会产生弯矩，然后得到该弯矩引起的弯曲变形，最后令薄层厚度趋于零，薄层应力梯度引起的弯曲变形曲率与一般梁理论推导的弯曲梁的曲率完全一致，最终证实薄层弯曲的原因是应力梯度。本文可以为学生深入理解梁弯曲与应力梯度提供一个有趣的视角。

Abstract: It is well-known that only normal stress keeps along the cross-section of a beam under pure bending moment, without transverse normal stress according to the famous Kirchhoff assumption. Consequently, the doubt may come out: Why does the beam bend under such a load? This paper will present a brief discussion to answer this question. Firstly, the gradient of the bending stress along the transverse direction of the beam results in bending moment; and then, this moment will cause the bending deformation of the beam; finally, this paper proves that the curvature of the bending deformation arising from the stress gradient just mentioned is exactly consistent with that of bending beam derived by general theory of beam. This evidence conclusively confirms the key point of this study, and can be an interesting view for students to deeply understand the analysis of bending beam, as well as the methodology of mechanics.

1. 引言

材料力学是工科学生的基础课。教学中，不仅要传授知识，而且要培养学生多思考，能逆向思维的能力。北航学子多年在大学生力学竞赛中取得优异成绩，与教学讨论的良好氛围是分不开的。材料力学中弯曲正应力推导是基于两个基本假设的：平面假设和单向受力假设 [1]。有聪明的学生提出了这样的疑问：若认为梁由无穷多的纵向纤维组成，根据单向受力假设，单拿出一个纵向纤维，当梁纵向纤维的横向尺寸趋于零时，通常可简化为两侧受到均匀力作用，它在单向应力状态下只应该发生伸长或缩短，它是怎么变弯的？本文对这个问题进行了研究。

2. 梁横向应力的数值方法研究

对于上述问题，笔者与多名材料力学教师进行过探讨，往往解释为横向挤压导致纤维弯曲，但这种说法与单向受力假设矛盾，而这个假设已经得到理论及实验的证实。

用数值方法也证实了小变形情况下没有横向挤压的结论，也就是说横向应力有限元计算结果是零。那么大变形情况下结果如何呢？对大变形条件下的轴向及横向应力进行有限元分析的结果如图1所示。由于大变形情况下梁两侧加载方向没随截面转动而发生转动，导致存在边界效应，其影响区域的横向最大应力约为纵向最大应力的5%。去除边界效应影响区域，中间区域基本没有横向挤压。显然，即使在大变形情况下，横向应力也极小，不应是纤维变形的主要因素。

(a) 梁轴向正应力计算结果(b) 梁横向挤压应力计算结果

Figure 1. Finite element results of beam stress under large deformation

图1. 大变形条件下梁应力的有限元分析结果

3. 纵向纤维应力梯度引起的变形分析

单根纵向纤维变弯的最主要影响因素到底是什么呢？本文从应力梯度的角度进行了探讨。通常在分析应力状态时，都是取无穷小尺寸的微体，并简化为受到均匀应力作用。其实，即使这时尺寸无穷小导致应力梯度也无穷小，微体还是可以发生弯曲变形的。下面以纯弯梁为例，在材料力学理论的框架内，对单层纵向纤维的弯曲变形进行讨论。

假设在任意梁上，距离中性轴为y_A的地方取高度为Δy_A的由纵向纤维组成的薄层，如图2所示。梁横截面上的正应力沿梁高度方向是线性分布的，也就是说存在应力梯度。尽管薄层上应力梯度非常小，产生的弯曲力偶也非常小，但是另一方面，薄层厚度很小也使薄层的抗弯刚度非常小，其弯曲变形正是由于这一应力梯度造成的。下面将详细进行分析计算。

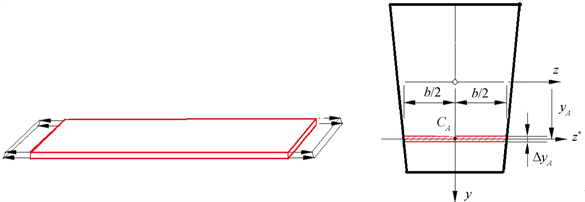
Figure 2. Schematic diagram of taking an arbitrary thin layer from the beam

图2. 梁中取薄层示意图

以该薄层为研究对象。由于薄层厚度Δy_A很小，该薄层可视为宽度为b的矩形截面梁。当然也可以将研究对象从纵向薄层改为纵向纤维，只是将薄层宽度b改为纤维宽度Δb即可，分析步骤和结论都是相同的，所以这里仅仅按薄层进行了计算。

薄层横截面上距离中性轴为y处取微面积bdy，如图3所示，其上的力为 $\sigma b\text{d}y$ ，该力对薄层形心轴z^*的距为 $\left[y-y_A\right]\sigma b\text{d}y$ ，进行积分即可得到薄层横截面所有力对z^*轴的距，也就是薄层应力梯度引起的弯曲力偶

$\Delta M={\displaystyle {\int }_{y_A-\Delta y_A/2}^{y_A+\Delta y_A/2}\sigma \left[y-y_A\right]b\text{d}y}$ (1)

其中，梁的弯曲正应力为

Figure 3. Micro-area in the section of the thin layer

图3. 薄层截面内取微面积

$\sigma =\frac{My}{I_z}$ (2)

$I_z$ 为整体梁的截面惯性矩。将其代入式(1)可得

$\Delta M={\displaystyle {\int }_{y_A-\Delta y_A/2}^{y_A+\Delta y_A/2}\frac{My}{I_z}\left[y-y_A\right]b\text{d}y}=\frac{Mb}{I_z}{\left[\frac{y^3}{3}-y_A\frac{y^2}{2}\right]}_{y_A-\Delta y_A/2}^{y_A+\Delta y_A/2}$ (3)

化简得到

$\Delta M=\frac{M}{I_z}\frac{b}{12}\Delta y_A^3$ (4)

可以看到，应力梯度引起的弯曲力偶与薄层位置y_A无关，只与薄层厚度Δy_A相关。

如果薄层处于中性层附近，则弯曲力偶引起的薄层曲率为

$\frac{1}{\rho }=\frac{\Delta M}{E{I}_z^A}$ (5)

其中， $I_z^A$ 为薄层截面惯性矩

$I_z^A=\frac{b\Delta y_A^3}{12}$ (6)

将式(4)、(6)代入式(5)，并进行化简后得到

$\frac{1}{\rho }=\frac{M}{E{I}_z}$ (7)

其余薄层则处于拉(压)弯组合变形情况，而不能视为单纯受拉或压，其曲率半径 ${\rho }_A$ 可以由其中性层曲率半径加(减)其到中性层的距离得到，

${\rho }_A=\rho +y_A=\frac{E{I}_z}{M}+y_A$ (8)

需要指出的是，当薄层厚度Δy_A趋于零时，ΔM趋于零，分析时如果简化为均匀应力状态，就会产生均匀应变，但事实上，根据(4)及(6)式，由于ΔM与 $I_z^A$ 同时趋于零，依然可以得到相同的中性层曲率

$\frac{1}{\rho }={\lim }_{\Delta y_A\to ０}\frac{\Delta M}{E\frac{b}{12}\Delta y_A^3}=\frac{M}{E{I}_z}$ (9)

这与整体分析时梁的中性层曲率公式是完全一致的。也就是说，在分析弯曲变形时，当薄层厚度趋于零，应力梯度依然是不能被忽略的。

通过这一实例告诉我们，导致纵向纤维弯曲的最主要因素是应力梯度，纠正了关于纤维弯曲主要影响因素是横向挤压应力的错误概念。

这个问题体现了材料力学教学中被忽视的一个知识点，即应力梯度对变形的影响。分析强度时微体各个面上应力一般是简化为均匀的，但即使微体所受应力梯度无穷小，微体也可以发生弯曲变形，所以分析变形时还是需要考虑应力梯度的。当然，应力梯度不仅影响变形，对疲劳、断裂的影响也很大，需要引起高度重视。

这个问题也可以作为开展研究型教学的一个切入点，推动学生与教师深入理解弯曲问题。对于弯曲问题还可进行一系列讨论，例如变截面梁弯曲切应力公式的讨论 [2] 及应用曲梁公式分析孔边应力集中 [3] 等。

参考文献