1. 引言
Progabil为氨基丁酸类药物,熔点133℃~135℃,沸点525.4℃ ± 50℃,水溶性37.16 mg/L,能直接激活GABA受体,该制剂能促进药物在脑内的传递,在中枢神经系统内外代谢成相应的酸,最后分解为氨基丁酸。药物在口服后2~3小时达到血药浓度峰值。它们几乎都是通过肝脏代谢的,相应的酸、氨基丁酸和氨基丁酸在服药几分钟后就会出现在大脑中。对癫痫、痉挛、运动障碍有较好的治疗作用。适用于癫痫、痉挛、帕金森病的治疗。在服用药物后,部分人群易出现诸如嗜睡、眩晕、疲劳及胃肠障碍等不良反应。
本文采用定量计算的方法对制剂的结构和红外光谱特性进行了研究,以期更好地了解药物的各种性质,为临床减少各种副作用的发生提供指导。
2. 计算方法
高斯计算软件广泛应用于化学计算领域 [1] [2] [3] [4],它提供了多种功能密度泛函方法,可用于计算分子能量和结构、过渡态能量和结构、化学键和反应能、红外和拉曼光谱反应路径和激发态性质 [5] [6]。除分子体系外,还可以计算溶液体系和周期体系 [7] [8]。本文系统地研究了普罗加比的分子结构和红外光谱分布。我们首先用GaussView软件构造了普罗加比的初始结构,然后用Gaussian 09在B3LYP/3-21G的水平上对其初始结构进行了优化,在此基础上,采用B3LYP/6-31+G (D, p)对其进行了结构优化和频率计算。在频率计算中没有虚拟频率,因此确定该构型为稳定构型。通过对频率计算结构的分析,得到了普罗加比分子的红外振动光谱,并对光谱中出现的谱线进行了识别,分析了谱线的形成机理。频率计算采用0.9613的修正系数 [9]。
3. 结果与讨论
3.1. 普罗加比分子结构
普罗加比分子的稳定构型如图1所示。在分子结构中共含有的H-C、C-C、C-O、C=O、C-F、C-Cl、C-N和H-N八种化学键,分子结构不具有良好对称性。在整个分子结构中含有2个环状结构,两个环状与氨基丁酸相连结,其中一个环状结构中含有一个F原子和一个O原子,在该环状结构中,各化学键键长变化如图2所示。分析发现,在该环状结构中,各C-C键键长变化较大,其中2C-1C键键长为1.359 Å,3C-2C键键长为1.468 Å,4C-3C键键长为1.488 Å,5C-4C键键长为1.443 Å,6C-5C键键长为1.356 Å。在该环状结构的其他化学键长中,31F-6C键长最长,为1.356 Å;而7H-1C、8H-2C和9H-5C三个H-C键的键长相差不大,分别为1.086 Å、1.085 Å和1.083 Å。
分子结构中另一个环状结构中含有一个Cl原子,各化学键键长变化如图3所示。在所形成的C-C键中,11C-10C键键长最大,为1.396 Å;13C-11C键键长最小为1.388 Å,而在环状结构的C-H键中,14H-11C和18H-13C键键长相等,均为1.084 Å,而16H-12C和19H-15C的键长也相差不大,分别为1.086 Å和1.084 Å。
氨基丁酸通过C-C键与两个环状结构相连结,其各化学键键长变化曲线如图4所示。在所含各C-C键重,35C-32C、27C-24C和32C-27C键键长均为1.531 Å,10C-20C键键长为1.486 Å,4C-20C键键长为1.404 Å。在氨基丁酸的骨架结构中,22N-20C键键长为1.360 Å,37N-35C键键长为1.364 Å,24C-22N键键长为1.460 Å。在氨基丁酸的侧链结构中,与37N相连的39H-37N和38H-37N键键长分别为1.007 Å和1.009 Å,23H-22N键键长为1.012 Å,25H-24C键键长为1.092 Å,而26H-24C键键长较之略长,为1.099 Å;与27C相连的28H-27C和29H-27C键的键长均为1.096 Å,与32C相连的33H-32C和34H-32C键键长分均为1.097 Å,36O-35C键键长为1.221 Å。
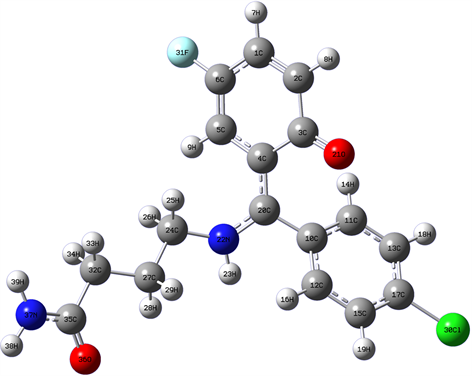
Figure 1. Stable structure of progabi
图1. 普罗加比分子的稳定构型
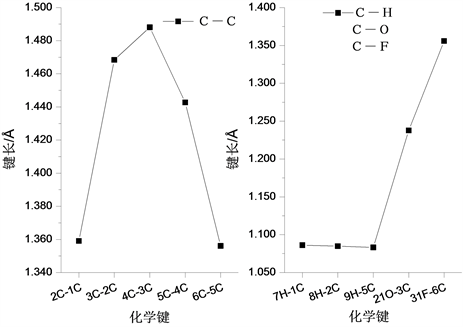
Figure 2. The variation curve of chemical bond length with the ring structure of F atom
图2. 含F原子环状结构的化学键长变化曲线
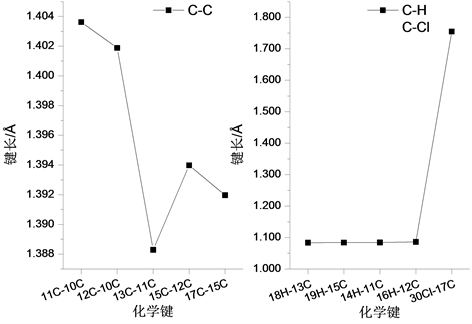
Figure 3. The variation curve of chemical bond length with the ring structure of Cl atom
图3. 含Cl原子环状结构的化学键长变化曲线
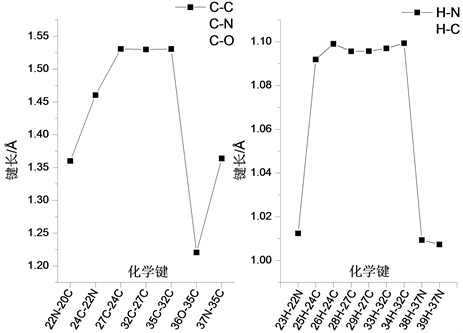
Figure 4. The variation curve of chemical bond length of side chian structure
图4. 侧链结构的化学键长变化曲线
在真个分子结构中,各原子形成的键角相对变化关系如图5~图7所示所示。分析发现在各形成的键角中出现了大量键角近似相等的现象。在各原子所形成的二面角中,∠4C-3C-2C-1C、∠5C-4C-3C-2C、∠6C-5C-4C-3C和∠17C-15C-12C-10C四个二面角均为0˚,∠7H-1C-2C-3C、∠8H-2C-1C-6C和∠18H-13C-11C-10C三个二面角均为180˚,参与形成相应二面角的四个原子处于同一平面内,而∠19H-15C-12C-10C、∠30Cl-17C-15C-12C和∠32C-27C-24C-22N三个二面角均为179˚,参与形成该三个二面角的四个原子近似处于同一平面内。
3.2. 普罗加比分子的红外振动光谱
红外振动光谱的强度主要取决于跃迁几率,而电子的跃迁几率又取决于红外电磁波的电矢量,跃迁偶极矩 [8]。与分子的永久偶极矩不同,跃迁偶极矩反应出的是振动时偶极矩变化的大小。因此,红外吸收强度取决于偶极矩的变化。如果振子过程中偶极矩变化较大,跃迁概率较大,谱强度较强;如果偶极矩在振动过程中变化不大,跃迁概率也相应较小,红外光谱强度较低 [9]。
图8给出了经频率分析后得到的普罗加比的红外光谱。结果表明,分子的正振动数大于光谱中实际谱线数,这主要是由于某些分子振型引起的分子偶极矩变化不大,存在简并现象。此外,红外光谱的每一谱线基本上都是由多个振动模式共同引起的 [10] [11] [12]。根据分子振动类型的不同,可将红外振动光谱分为三个区域,即:(0~1000) cm−1、(1000~3000) cm−1和(3000~4000) cm−1。
在(0~1000) cm−1区域,主要以分子内环状结构的呼吸振动、各部分的整体转动和摆动为主,最强峰出现在90 cm−1处,这是由含37N的NH2基团绕35C-37N键的整体旋转造成的。第二强峰出现在576 cm−1
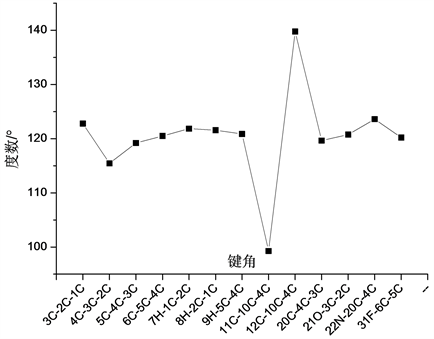
Figure 5. The variation curve of bond angle of ring structure containing F atom
图5. 含F原子环状结构各键角变化曲线
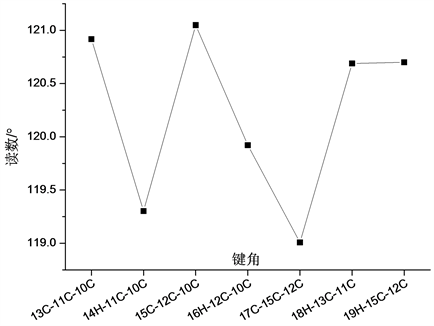
Figure 6. The variation curve of bond angles in ring structure of Cl atom
图6. 含Cl原子环状结构各键角变化曲线
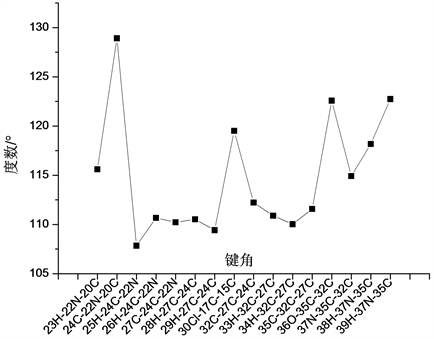
Figure 7. The variation curve of bond angle of side chain structure
图7. 侧链结构各键角变化曲线
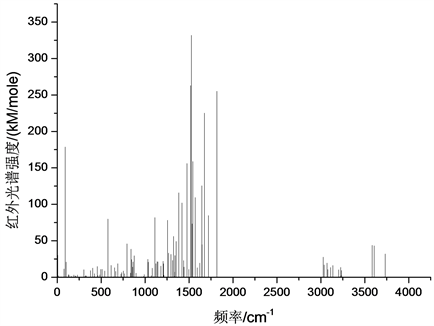
Figure 8. Infra-red specturm of progabi
图8. 普罗加比分子红外光谱
处,是由双环结构的呼吸振动和NH2基团整体摆动的联合振动引起的。在795 cm−1处的振动峰是由35C-36O和30Cl的复合振动引起的,分子振动模式如图9所示。841 cm−1处的振动峰值是由7H和8H左右摆动、14H和18H左右摆动、16H和19H左右摆动引起的,分子振动模式如图10所示。16H和19H左右摆动和含10C环结构的呼吸振动在877 cm−1处产生一个强共振峰,而含有1C的环形结构的呼吸振动、21O和31F的左右摆动在847 cm−1处引起一振动峰值。此外,在25 cm−1、71 cm−1和627 cm−1处出现了没有红外活动的现象,这主要是因为相应的振动模式不会引起分子偶极矩的变化。25 cm−1处的振型主要是31F左右摆和21O左右摆动的复合振动,71 cm−1位置的振动模式主要是含1C和环状结构绕4C-20C的整体转动,而627 cm−1位置的振动模式主要与氨基丁酸侧链结构的整体摆动相对应。在864 cm−1位置出现了双重简并现象,分别与23H和16H的整体摆动、14H和19H的整体摆动相对应。
在(1000~3000) cm−1区域,分子的振动模式主要为面外摇摆振动、剪式振动和面内摇摆振动。光谱振动峰主要在(1000~1850) cm−1范围内,而在(1850~3000) cm−1区域没有共振峰出现,其中区域的最强峰出现在1527 cm−1位置,是由含28H和29H的剪式振动引起地,它也是整个红外光谱的最强峰,分子振动模式如图11所示。区域次强峰出现在1517 cm−1位置,它是由25H和26H的剪式振动,以及28H和29H的剪式振动的复合振动引起地,它也是红外光谱的次强峰,分子振动模式如图12所示。而25H和26H的剪式振动,以及28H和29H的剪式振动的复合振动在1542 cm−1位置也引起一振动峰,但28H和29H剪式振动的振动强度较1517 cm−1位置的对应的28H和29H剪式振动强度低,分子振动模式如图13所示。1817 cm−1位置振动峰是由38H和39H的剪式振动引起地,25H的面内摇摆振动和26H的面外摇摆振动的复合振动在1676 cm−1位置引起一较强共振峰;在1476 cm−1位置的振动峰是由33H和34H的面内摇摆振动引起地,1645 cm−1位置的共振峰是由38H和39H的剪式振动引起地,振动模式如图14所示。28H和29H的面外摇摆在1384 cm−1位置引起一较强共振峰。25H和26H的面内摇摆振动和在1571 cm−1位置引起一共振峰。1418 cm−1位置谱峰是由38H和39H的扭曲振动和33H和34H的面外摇摆振动的复合振动引起地。33H和34H的扭曲振动和28H和29H的剪式振动的符合振动在1721位置引起一较强共振峰。
此外,在该区域的1214 cm−1、1070 cm−1、1098 cm−1和1334 cm−1四个位置的谱峰出现了无红外活性的现象,其中1214 cm−1位置振动峰是由16H、19H的剪式振动和14H、18H的剪式振动的复合振动引起地,1070 cm−1位置的振动峰是由33H和34H的面外摇摆振动、28H和29H的面外摇摆振动和25H和26H的面外摇摆振动的复合振动引起地,1098 cm−1位置振动峰主要是由33H和34H的扭曲振动引起地,而1334 cm−1位置共振峰是由14H、18H面内摇摆振动及16H和19H的面内摇摆振动的复合振动造成地。在1721 cm−1位置出现了双重简并现象,其分别与25H、26H的扭曲振动和33H和34H的扭曲振动的复合振动,以及25H、26H的扭曲振动和7H、8H的面外摇摆振动的复合振动相对应。
在(3000~4000) cm−1区域,分子振动均为伸缩振动,该区域共振峰数量偏少,强度也较低。区域中的最强峰出现在3584 cm−1位置,它是由23H的对称伸缩振动引起地,分子振动模式如图15所示。区域次强峰出现在3606 cm−1位置,其对应的分子振动模式主要是38H和39H的对称伸缩振动,分子振动模式如图16所示。在3733 cm−1位置出现的共振峰主要是由38H和39H的反对称伸缩振动引起地,其分子振动模式如图17所示。26H和34H的伸缩振动在3028 cm−1位置引起一较强共振峰,而28H和29H的对称伸缩振动在3069 cm−1位置引起一共振峰,分子振动模式如图18所示。3038 cm−1位置出现的共振峰主要是由33H和34H的对称伸缩振动引起地,3136 cm−1位置出现的共振峰主要是由25H的伸缩振动引起
地,而3226 cm−1位置出现的共振峰主要是由7H和8H的对称伸缩振动引起地。28H和29H的反对称伸缩振动在3110 cm−1位置引起一共振峰,34H和34H的反对称伸缩振动在3078 cm−1位置引起一共振峰,7H的伸缩振动在3204 cm−1位置引起一共振峰。此外,3226 cm−1位置出现了无红外活性的现象,其振动模式主要为14H和18H的反对称伸缩振动。
4. 结论
本文利用Gaussian计算软件在B3LYP/6-31 + G (d, p)水平上确定出了普罗加比分子的稳定构型,并通过频率计算析的方法得到了普罗加比分子的红外振动光谱。对分子结构特点进行了详细的分析,然后对红外光谱中的谱线进行了指认归属。研究发现,普罗加比分子的红外振动光谱可划分为(0~1000) cm−1、(1000~3000) cm−1和(3000~4000) cm−1三个区域,每个区域中的谱线所对应的分子振动模式有所不同,其中在(0~1000) cm−1区域,振动主要为环状结构的呼吸振动、各部分的整体转动和摆动,而在(1000~3000) cm−1区域,分子的振动模式主要为分子的弯曲振动,该区域存在有光谱的最强峰和次强峰;在(3000~4000) cm−1区域,振动类型均为伸缩振动。此外,光谱中存在无红外活性和简并现象,致使实际光谱数量比实际数量少。