基于DLR模型的PM10–能见度–湿度相关性研究

Correlation Study of PM10-Visibility-Humidity Based on DLR Model

摘要: 针对当前大数据在单机运算时间过长，对硬件设备要求高的问题，为此提出基于云环境下使用分布式逻辑回归算法DLR (Distributed Logistic Regression)模型对PM10与能见度以及湿度之间的相关性问题，根据二分类思想，将能见度、湿度作为特征值，PM10作为标签值使用逻辑回归算法构建模型对其进行分析，实验结果表明，在同一湿度范围下能见度值越小，大气气溶胶PM10浓度偏大，在同一能见度范围下湿度值越大，大气气溶胶PM10浓度偏低。并且DLR算法模型在时间性能方面要优于传统回归模型，具有更好的鲁棒性以及实时性。

Abstract: Considering the problem that the current big data has a long stand-alone operation time and high requirements for hardware devices, this paper proposes the use of the Logistic Regression (DLR) model in the cloud environment for the correlation between PM10 and visibility and humidity. According to the idea of two classifications, visibility and humidity are used as feature values, and PM10 is used as a tag value to construct a model using a logistic regression algorithm. The experimental results show that under the same humidity range, the smaller the visibility value is, the higher the PM10 concentration of atmospheric aerosol is. The higher the humidity value in the same visibility range, the lower the concentration of PM10 in atmospheric aerosols. And the DLR algorithm model outperforms the traditional regression model in terms of temporal performance, and has better robustness and real-time performance.

1. 引言

在目前的研究中，经常使用数学领域中的统计学方法对湿度、大气能见度与气溶胶PM10进行研究，如文献 [1] 用标准化降水指数作为为干旱指标，分析贵州省年度和季节的干旱发生频率的变化特征；刘艳萍等 [2] 应用统计学和Arc GIS软件分析中国四大工业基地主要城市大气颗粒物污染的时间及空间分布特征，并利用SPSS软件对大气污染物PM10、SO₂、NO₂、CO、O₃和PM2.5的相关性进行分析；文献 [3] 分析显示PM10浓度增大以及颗粒物吸湿性增长可导致能见度数值降低。但这类方法存在人为影响的客观因素。近年来，更多的学者寻找其他的替代方法。20世纪80年代以来人工智能领域兴起，人工神经网络成为研究的热点。石灵芝等人提出基于BP人工神经网络 [4] 的大气颗粒物PM10质量浓度预测，建立人工神经网络模型捕捉污染物浓度与气象因素间的非线性影响规律，能够准确预测大气PM10质量浓度的实时变化。D. K. Papanastasiou等人提出使用神经网络 [5] 和多元回归模型 [5] 以预测一个中型的地中海城市PM10水平，两个模型都能够较好的预测PM10实时日均值。

然而，气象领域在处理气象数据的问题上使用的多是投入耗费大的传统方法。对于硬件设备的要求过高，普通的单机运算已经无法满足大数据时代的要求。云计算，一种按量付费模式，融合了分布式计算、并行计算、网络存储等技术的新型产物。能够方便、快速、按需分配的完成客户端的运算任务。云计算的低成本运算快让更多研究者用这种方法解决大数据的运算问题。郑湃等 [6] 提出云计算环境下面向数据密集型应用的数据布局策略与方法，介绍了一种三阶段数据布局策略以解决跨数据中心数据传输、数据依赖关系和全局负载均衡三个问题，实验分析所提出的方法在时间性能上得到有效提高。王晓燕等 [7] 提出基于云计算环境中面向OLTP应用的数据分布研究，提出以数据分片、数据分片和负载执行为变量对基于计算环境中大数据OLTP应用的数据分布问题进行详细归纳分析。张石磊/武装提出一种基于Hadoop云计算平台的聚类算法优化的研究 [8]，对首先选定初始聚类中心的并行K-means聚类算法进行相关实验验证优化后的算法在时间性能上更优。在气象数据方面，云计算技术也有相应的研究。如潘吴斌提出的基于云计算的并行K-means气象数据挖掘研究与应用，并行K-means算法可以有效解决分布式数据问题，而大规模数据对运算负荷暴增，为此提出在Hadoop平台上实现K-means算法的MapReduce并行化 [9]，实验表明K-means聚类效果较好，运行时间较传统方法更优，具有一定的应用意义。如文献 [10] 基于改进贝叶斯网络的气象数据预测算法研究，提出Hadoop平台上使用贝叶斯网络方法对气象数据进行预测，所提出的改进方法与现有的气象预测算法有效地提高了预测精度。以上研究表明，云计算可以有效的解决大规模数据的运算问题，并且可以有效应用在气象领域方面。

为此，本文基于中国气象局气象数据中心和南宁市环保局环境监测站历年气象数据提出了基于云环境下DLR (Distributed Logistic Regression)模型用于能见度、湿度与气溶胶PM10相关性的研究，实验分析表明，湿度区间一致大气气溶胶PM10浓度越大能见度就越小，能见度区间一致大气气溶胶PM10浓度越低湿度越大。实验结果还发现湿度介于40%~90%，能见度介于8~19 km DLR模型预测效果最好。

2. 逻辑回归定义

在介绍逻辑回归前，我们先简单了解一下线性回归。线性回归的核心思想是：相当于拟合一条直线，设定界限中间值0.5，归属一类，归属为另一类。线性回归可以用于一些分类问题 [11]，但存在的缺点是，线性回归的鲁棒性太差，导致训练的性能较差。

逻辑回归主要用于二分类问题，简单地可以理解为：分类结果要么是，要么是。本实验将PM10溶度大于0.15 mg/m³设定为，将PM10溶度小于0.15 mg/m³设定为。大气能见度指标、湿度指标为自变量，对应y的数学期望如式(1)：

$E\left(y|x_i\right)=p\left(y=1|x_i\right)$ (1)

其中， $p\left(y=1|x_i\right)$ 表示在 $x=x_i$ 时 $y=1$ 的概率。那么，建立逻辑回归问题可以简单理解为：y在[0,1]内取某个值的概率与x的函数关系。本文采用极大似然估计利用特征数据集以及分类数据集构建逻辑回归模型如式子(2)：

$p=p\left(y=1|x\right)=\frac{\exp \left(\alpha +\beta x\right)}{1+\exp \left(\alpha +\beta x\right)}$ (2)

变换得式(3)：

$\frac{p}{1-p}=\exp \left(\alpha +\beta x\right)$ (3)

其中p表示溶度大于0.15 mg/m³， $1-p$ 表示溶度小于0.15 mg/m³， $\alpha$ 、 $\beta$ 是模型参数。式子(2)为一元逻辑回归模型，对取得式子(4)：

$\text{logit}\left(p\right)=\ln \left(\frac{p}{1-p}\right)=\alpha +\beta x$ (4)

式(4)是关于的线性函数，式子(2)是关于的非线性函数。实际应用中，变量会有多个，此时就需要引用多元逻辑回归，通过式子(3)和式子(4)可以得到式(5)、式(6)。

$p=p\left(y=1|x_1,\cdots ,x_k\right)=\frac{\exp \left(\alpha +{\displaystyle \underset{i=1}{\overset{k}{\sum }}{\beta }_i{x}_i}\right)}{1+\exp \left(\alpha +{\displaystyle \underset{i=1}{\overset{k}{\sum }}{\beta }_i}{x}_i\right)}$ (5)

$\text{logit}\left(p\right)=\ln \left(\frac{p}{1-p}\right)=\alpha +{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k$ (6)

DLR模型设计思想

云计算环境下，DLR模型设计思想主要分以下过程：

1) 训练样本集，

2) 对测试集分类结果进行结果预测。

根据上述逻辑回归模型定义可以设定属于正类概率的DLR模型回归方程如式(7)：

$f\left(x,\beta \right)=p\left(y=1|x_1,x_2\right)=\frac{\exp \left({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2\right)}{1+\exp \left({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2\right)}$ (7)

其中DLR模型回归方程的参数 $\beta =\left({\beta }_0,{\beta }_1,{\beta }_2\right)$ 可以从训练结果中得到，向量 $x=\left(x_1,x_2\right)$ 为能见度和湿度。于是可以得出y的概率如式(8)：

$P\left(y|x,\beta \right)=f{\left(x,\beta \right)}^y{\left[1-f\left(x,\beta \right)\right]}^{1-y}$ (y=0或1) (8)

采用极大似然估计建立似然函数L如下(9)：

$L=P\left(y|x,\beta \right)={\displaystyle \underset{i=1}{\overset{n}{\prod }}f{\left(x_i,\beta \right)}^{y_i}{\left[1-f\left(x_i,\beta \right)\right]}^{1-y_i}}$ (9)

令 $\theta =\ln L=\ln P\left(y|X,\beta \right)={\displaystyle \underset{k=1}{\overset{N}{\sum }}\left(y_i\ln f\left(x_i,\beta \right)+\left(1-y_i\right)\left(1-f\left(x_i,\beta \right)\right)\right)}$，其中，x_i为数据集X得第i个记录，y_i是第i个记录的分类结果，计算 $\theta$ 的最大值可以得到参数：

$\beta =\max \ln P\left(y|x,\beta \right)$ (10)

本文采用梯度下降法解极大似然估计：

${\beta }^{i+1}={\beta }^i+\epsilon \frac{\partial \ln P\left(X,y,\beta \right)}{\partial \beta }={\beta }^i+\epsilon X^{\text{T}}\left(y-f\left(X,\beta \right)\right)$ (11)

云计算环境下分布式DLR模型基本步骤如下：

1) 初始化参数，若干运算节点同时训练训练数据集。

2) 各运算节点分别计算对应样本的以及样本各特征值与的积。

3) 各节点求和得出行向量并转置得到的值。

4) 判断是否收敛，是则运算结束，否则执行(1)、(2)，直至收敛。

3. DLR模型实验结果与分析

3.1. 实验数据集

数据集为广西南宁环保局环境监测站以及中国气象局气象数据中心1980~2014年气象数据，包括气溶胶、能见度、湿度等特征值。

实验过程将湿度、能见度各划分三个区间范围，湿度的三个区间分别是：湿度值<40%；40% ≤ 湿度值 ≤ 90%；湿度值>90%。能见度的三个区间分别是能见度值<8 km；8 km ≤ 能见度值 ≤ 19 km；能见度值>19 km。然后使用数据库SQL语句将这些区域进行两两组合构成9种组合方式，再分别通过SQL语句连接PM10数据表，共9个实验数据表源，分别是数据表1为湿度值<40%，能见度值<8 km对应的气溶胶PM10值；数据表2为湿度值<40%，8 km ≤ 能见度值 ≤ 19 km对应的气溶胶PM10值；数据表3为湿度<40%，能见度值>19 km对应的气溶胶PM10值；数据表4为湿度值>90%，能见度值<8 km对应的气溶胶PM10值；数据表5为湿度值>90%，8 km ≤能见度值 ≤ 19 km对应的气溶胶值；数据表6为湿度>90%，能见度值>19 km对应的气溶胶PM10值；数据表7为40% ≤ 湿度值 ≤ 90%，能见度值<8 km对应的气溶胶PM10值；数据表8为40% ≤ 湿度值 ≤ 90%，8 km ≤ 能见度值 ≤ 19 km对应的气溶胶PM10值；数据表9为40% ≤ 湿度值 ≤ 90%，能见度值>19 km对应的气溶胶PM10值，以下数据源表格以数据表2为例，数据源内容如表1所示(即湿度值<40%，8 km ≤ 能见度值 ≤ 12 km组合的表格数据源)，实验结果截图以数据表2和数据表8为例。

Table 1. Part data of data table 2

表1. 数据表2部分数据

Figure 1. Experiment procedure of DLR model

图1. DLR模型实验过程

3.2. 实验过程

DLR模型是通过二分类的思想来对输入的数据源进行预测分析，将能见度、湿度作为特征列，对气溶胶PM10标签列进行预测分析。在实验当中，我们分为四个部分，分别是读取数据源以及对数据预处理；使用直方图、全表统计对数据表进行统计分析；DLR模型的训练以及预测分析。最后通过评估模型分析DLR模型的预测准确率，以及哪个区间范围内的数据更适合用来预测PM10的值，实验过程如图1所示。

3.3. 实验结果分析

以数据表2、数据表8作为分析对象，训练前按照0.3比例划分数据，即30%作测试集，70%作训练集。设置迭代次数100；正则系数1；最小收敛误差0.00001。DLR模型输出如图2、图3所示。

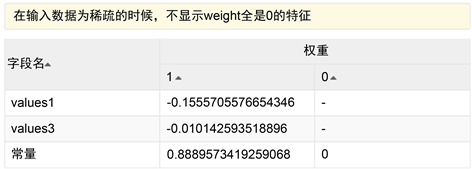
Figure 2. DLR model output results of data Table 2

图2. 数据表2 DLR模型输出结果

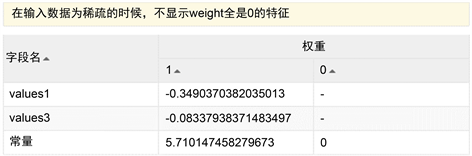
Figure 3. DLR model output results of data Table 8

图3. 数据表8 DLR模型输出结果

其中系数值越大影响越大，+表示正相关，−表示负相关。图2中表明湿度、能见度与PM10呈负相关。数据表2和数据表8为数据源的DLR模型准确性分别为0.6649和0.8279即ROC面积，值越大表明分类效果越好，如图4、图5所示。

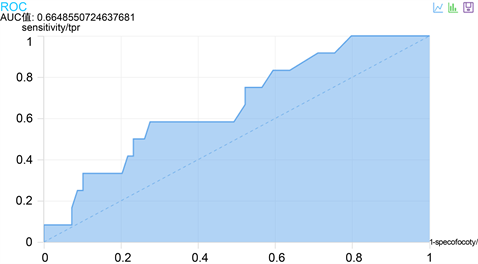
Figure 4. DLR model roc curve of data Table 2

图4. 数据表2 DLR模型ROC曲线

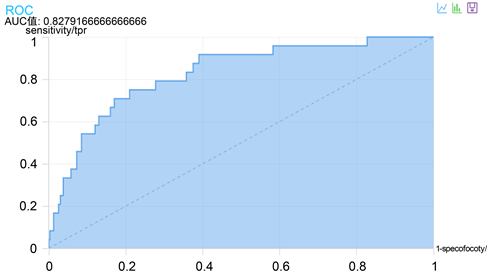
Figure 5. DLR model roc curve of data Table 8

图5. 数据表8 DLR模型ROC曲线

下面给出了DLR模型数据表2、数据表8的预测值与原值拟合图(见图6，图7)，进一步说明本文提出的DLR模型较好的预测性能。

数据源的相关结果为表1 (湿度值<40%，能见度值<8 km) AUC值为0.6671；表2 (湿度值<40%，8 km ≤ 能见度值 ≤ 19 km) AUC值为0.6648；表3 (湿度值<40%，能见度值>19 km) AUC值为0.8695；表4 (湿度值>90%，能见度值<8km) AUC值为0.5518；表7 (40% ≤ 湿度值 ≤ 90%，能见度值<8 km) AUC值为0.7876；表8 (40% ≤ 湿度值 ≤ 90%，8 km ≤ 能见度值 ≤ 19 km) AUC值为0.8279，表9 (40% ≤ 湿度值 ≤ 90%，能见度值>19 km) AUC值为0.5。实验结果分析主要依据预测准确率即AUC的值以及特征列的相关系数。通过实验证明湿度值在40%~90%之间，能见度值在8~19 km之间效果最好即数据表8，其次是湿度值在 40%~90%之间，能见度值小于8 km即数据表7。效果最差的是湿度值小于40%，能见度值在8 km~19 km之间即数据表2。并且针对上述各个数据表的实验，特征列values1的相关系数都比values3的相关系数大。表九的分析结果出现反常，此表的范围为40% ≤ 湿度值 ≤ 90%，能见度值>19 km，这个区间被称为“非常好”能见度，本文不做参考对象，同时表3实验结果AUC值也偏大，考虑样本数的情况，样本数太小，不能作为评估对象。表5、表6两个数据表中符合条件的样本数太少，并且只有一个类别，故无法得到实验结果。

Figure 6. Fitting the predicted and original values of DLR model in data Table 2

图6. 数据表2 DLR模型预测值与原值拟合图

Figure 7. Fitting the predicted and original values of DLR model in data Table 8

图7. 数据表8 DLR模型预测值与原值拟合图

从实验结果分析可知，湿度指标在40%~90%之间，能见度指标在8 km~19 km之间，预测PM10值正确率最高，并且在同一湿度范围下，PM10值与能见度值成反比；在同一能见度范围下，PM10值与湿度值成反比。相比湿度指标，能见度指标相关性更高。针对本文研究的数据集，DLR模型在预测正确率上比较高。

4. DLR模型与传统回归模型时间性能的比较

如图8所示，DLR模型在时间性能上要优于传统的回归模型，基本在所有划分的数据源表上运行速度都明显提高，从运行时间性能上比较进一步证明了本文提出的DLR算法在PM10–能见度–湿度相关性研究上具有较好的性能，鲁棒性更强。

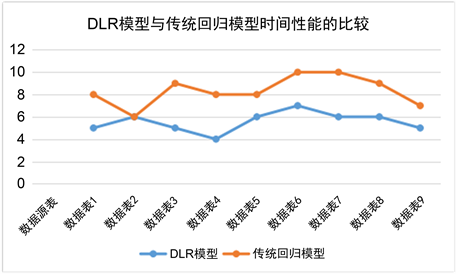
Figure 8. Comparison of running time between DLR model and traditional regression model

图8. DLR模型与传统回归模型运行时间比较

5. 结论

本文提出一个基于云计算环境的DLR模型，所用模型用于PM10–能见度–湿度相关性研究模型总体得分较高，鲁棒性强，模型得分存在差异是由于符合条件数据样例数不同造成。从实验结果分析可知，湿度指标在40%~90%之间，能见度指标在8~19 km之间，预测PM10值正确率最高，并且在同一湿度范围下，PM10值与能见度值成反比；在同一能见度范围下，PM10值与湿度值成反比。相比湿度指标，能见度指标相关性更高。此外DLR算法模型在时间性能方面要优于传统回归模型。云计算环境下DLR模型的验证对于实际应用具有一定可行性。本文研究存在如下不足：实验气象因子(如风速、降水等)考虑欠缺，后续工作考虑加入更多的影响因子进行实验研究。

基金项目

2018年广西高校中青年教师基础能力提升项目(NO.2018KY0699)：云环境下基于机器学习分析广西PM10的相关性研究；2020年度广西高校中青年教师科研基础能力提升项目(2020KY23019)：基于深度学习的桂中地区PM2.5浓度预测模型研究；2020年广西高校中青年教师基础能力提升项目(NO.2020KY23026)；2020年校级本科教学改革工程一般项目A类(NO.2020GKSYGA01)；来宾市智慧农业及农业大数据应用研究团队(GXKS2020QNTD02)。