1. 引言
储层预测是储层评价研究中的重要问题,而评价储层的好坏的重要岩石物性指标之一为孔隙度。测井解释研究工作之一就是如何利用现有的岩心样本数据预测并解释全井段的地质属性。概率与数理统计强调用样本特性参数去估计总体特性参数,常用的方法有矩估计、极大似然函数及最小二乘法。但由于试验数据存在一定不可避免误差,如:量具仪器超过额定检校周期、人工数据传递失误等。针对该类情况,在二十世纪初,研究概率与数理统计的相关数学家们总结出了采用置信区间消除残差等方法来控制误差确保估计精度。然而现实存在的误差远超理论误差,为了应对致密碳酸盐岩储层这种非均质性极强的地层,目前测井解释模型已经运用了多种非线性方法,如分段最小二乘法 [1]、人工神经网络法 [2]、数值模拟法 [3] 等。近几年来,许多研究者在支持向量机对于储层的孔隙度预测方面取得了较大的研究成果。乐友喜等 [4] 在胜利油田某区块应用支持向量机法,以地震波波形作为输入向量,进行了砂体孔隙度和含油性预测,预测结果与已知结果吻合较好。张尔华等 [5] 在地震属性组合的基础上确定支持向量机模型,进而预测火山岩储层厚,并在实际应用中取得了良好效果。熊晨皓等 [6] 利用支持向量机方法对珠–坳陷恩平组致密砂岩储层某井进行砂体孔隙度预测,证明了采用粒子寻优法下的支持向量机对实现少量样本分类具有显著的准确性。
由于岩心的取芯和测试费用较高,岩心测量数据一般较少且不连续,针对碳酸盐岩储层复杂的岩石架构下难以寻得合适的方程模型对孔隙度进行预测,故在支持向量机分类的基础上,根据岩心柱结合测井成像图片确定储集类型并取样,其后进行样本训练及全井段预测,确定沿深度方向岩层的各储集类型。通过对比分析各类储层电性特征,根据不同岩石的储集类型定向建立多元回归方程对孔隙度进行预测。
川中北部磨溪–高石梯地区是四川盆地天然气的主要产区,其主力储集层为震旦系灯影组和寒武系龙王庙组,其中龙王庙组厚度受古地貌影响显著,呈北西偏薄、南东偏厚的特征,岩石类型主要有砂屑白云岩、残余砂屑白云岩以及细–中晶白云岩。这些岩石的裂缝、孔洞比较发育,具有良好的储层发育条件,为油气的形成奠定了基础。震旦系灯影组的沉积厚度较大,分布范围较广,主要发育浅灰色微–粉晶白云岩、藻白云岩,其中灯二段和灯四段均为良好的含气层系。储层岩石结构主要以中白云岩为主,孔隙度分布在10%~20%,储层间的非均质性较强 [7]。
2. 原理分析
2.1. 基于MATLAB支持向量机分类(LIBSVM)应用
MATLAB与Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等。用MATLAB来解算问题要比用C,FORTRAN等语言完成相同的事情简捷得多。同时也可用MATLAB软件便利的调用各种工具箱,如:神经网络工具箱、曲线拟合工具箱及支持向量机等 [8]。
如果我们在低维空间里找不到一个线性分类面把样本分开,支持向量机就为我们提供了一个思路:将数据从低维空间映射到高维空间后,就很可能使得这堆数据线性可分。比如说,我们要在猫科动物这个特征很局限的“低维空间”里去分猫和老虎,是比较困难的,因为他们很多特征比较相近。但是,如果我们有了更多的参考依据,从生物界的视角,即一个“高维空间”再去区分猫和老虎,我们就有了更多的理由来做出科学的辨别。
2.1.1. 调用MATLAB支持向量机分类器(LIBSVM)相关函数
可先通过安装MATLAB支持向量机分类器(LIBSVM)安装包 [9],对样本进行训练及其后的预测需调用下列函数:
(1)
式中,train_label——训练集样本标签(储集类型);
train_matrix——训练集样本;
model——待训练模型;
'libsvm_options'——其他参数选项。
(2)
式中,test_label——测试集样本标签(储集类型);
test_matrix——测试集样本;
model——已训练好的模型;
predict_label——预测后样本标签;
accuracy——预测准确度。
2.2. 基于MATLAB定向回归拟合原理
在统计学中,回归分析(regression analysis) [10] 指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量的多少,分为一元回归和多元回归分析。按照自变量和因变量之间的关系类型,又可分为线性回归分析和非线性回归分析。广泛的应用于各项研究。针对有时样本过于离散,无论是采用单元线性回归还是多元线性回归,其决定系数R2值依旧不理想,针对该类现象,通常的做法是删除残差较大的样本点,重新拟合回归方程,进而获取较大的R2值。由于该类办法的随机性较大的削减了样本真实性,造成样本失真,进而影响了预测效果。基于前人的研究上,经过大量的试验与数据论证,开发定向多元回归分析处理该类问题。
2.2.1. 定向多元回归分析原理
最小二乘法定义不同的样本集具有唯一且单一的回归方程使其决定系数R2值达到最大,但往往“最优方程”却不能得到“最优解”,其原因多重各样无法臆测。需要人工反向修正以修订正确的拟合方向,得到更合理的预测结果。对于样本集合:
(3)
对于各样本的不同属性参数可用矩阵P表示:
(4)
选取两个主控因素进行二维平面散点图分析,可调用MATLAB绘图plot函数 [11] 进行绘制:
(5)
通过MATLAB ginput()函数 [12] 可以方便快捷的在图上选取两个坐标点并获取坐标点数据,再根据两数据点坐标确定直线方程:
(6)
根据直线方程删除偏离该直线附近的样本点,最后获取定向回归目标样本集其代码如下:
(7)
式中,rint——为残差容许区间,经过大量试验,取1~1.5为最佳。定向拟合如图1所示:
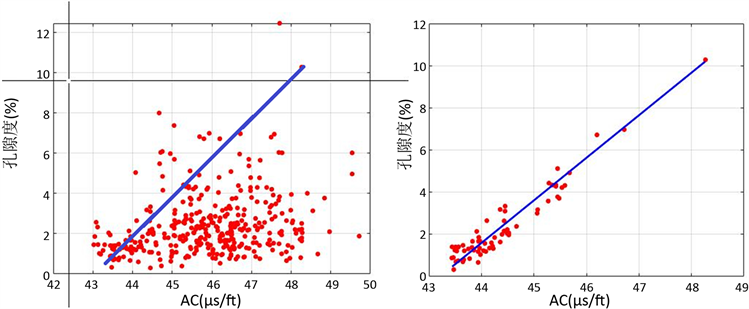
Figure 1. Process chart of directional fitting
图1. 定向拟合过程图
最后根据定向拟合获取的样本进行多元线性回归拟合,最终确定最优回归方程 [13]。
(8)
式中,
为回归系数。
3. 孔隙度预测过程
3.1. 数据标准化
由于少部分井测井原始曲线获取条件的差异,不同井测井仪器型号不统一,仪器操作人员的熟练程度不同以及井下环境不一样等因素,使得各井相同的地层、相同的岩性在同种测井曲线上的响应值具有一定的系统误差,这些差异会直接影响到测井储层参数的计算精度,给储量参数的准确计算带来一定的不确定性,要消除这些非地质因素的影响,使测井资料更真实地反映地层的实际情况,有必要对测井数据进行标准化,避免在之后的预测工作中陷入“失之毫厘,差之千里”的困境,针对不同井测井曲线深度不一致等问题,采用线性内插归一化的方式矫正。本文通过MATLAB 2018a软件编程实现对GR、DT、DEN、CNL、RT等测井曲线的批量标准化及调用interp1函数 [14] 进行深度值线性内插预处理。
3.2. 样本分类与预测
3.2.1. 储层的分类
本文结合岩心样本,选择具有取心资料的测试进行物性分析,结合成像测井 [15] 分别确定出这些典型层位的物性特征,在此基础上总结出了各类产层的孔隙度大小及储集能力。根据上述方法,可将A地区灯二段储层按照储集物性的好坏依次分为I、II、III、IV四类储层,各类储层的划分标准如表1所示。

Table 1. Reservoir classification and evaluation table of Denger formation in area A
表1. A地区灯二段储层分类评价表
其中I类为在自然开采条件下能够获得较好产能的储层;II类为自然开采条件下基本能够获得工业产能的较好储层;III类储层在自然开采条件下不能达到工业的差储层;IV类储层为含油性很差的非储层。
3.2.2. 样本选取及储集类型预测
将磨溪–高石梯13口重点井灯二段的960个实测岩心样本依据照表1分为四类。各类样本分布较均匀,随机选取其中的70%作为训练样本,剩下的30%样本作为测试样本,模型样本与训练样本的分配如表2所示。

Table 2. Sample distribution of Denger formation in area A
表2. A地区灯二段样本分配表
所有样本数据根据测井响应识别的原则,选取代表地层特征的3个参数,其中GR为伽马,DT为声波,CNL为中子密度。本次建模使用MATLAB 2018a支持向量机(LIBSVM)用训练后的模型对13口重点井进行了储集类型预测。
3.2.3. 预测结果分析
最终训练报告显示,样本集预测正确率为96.36%,测试集预测正确率为92.33%。根据预测结果,通过对储集类型电性参数的分析发现不同储集类型对DT声波时差有显著的相关性。其结果如图2所示。
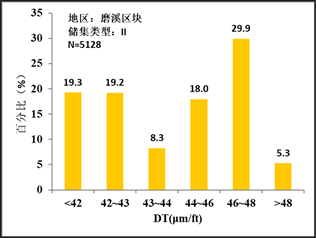
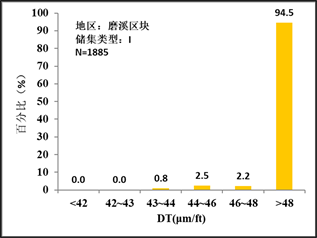
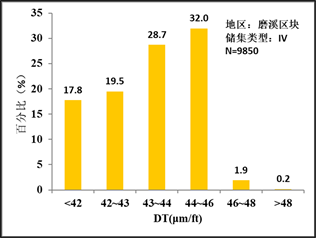
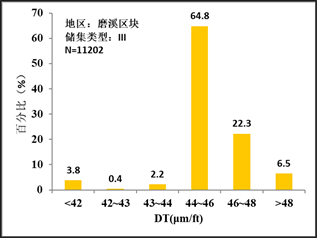
Figure 2. Distribution of DT values of reservoir types in Moxi block
图2. 磨溪区块储集类型DT值分布图
通过对比各类样本的储集类型声波值分布区间,可以明显的划分出各类储层的差异及特征。通过整理得到结论如表3所示:

Table 3. Characteristics of acoustic value of each reservoir type in the Denger formation in Moxi area
表3. 磨溪地区灯二段各储集类型声波值分布特点
3.3. 定向拟合及孔隙度值预测
在储层类型划分的基础上,确定以声波值为主控因素的前提下,采用逐步回归法 [16] 对孔隙度进行预测,对不同储集类型分别建立不同回归方程定向拟合,并预测孔隙度。
3.3.1. 定向拟合
选取磨溪区块A、B、C井共计样本362个,孔隙度值分布在5%~13%,声波值分布在43~51 μm/ft,并根据前叙述结论各储集类型声波值的划分特点,分区块定向拟合(图3)并建立回归方程。
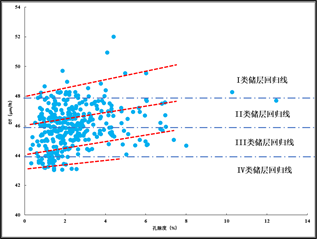
Figure 3. Chart of directional fitting of reservoir type
图3. 储集类型定向拟合效果图
3.3.2. 回归方程的确定
在定向拟合的基础上,新确立4类样本,其中I类样本13个,II类样本14个,III类样本154个及IV类样本194个,在此基础上进行逐步回归法建立回归方程对孔隙度进行预测,各类回归方程如下:
(9)
(10)
(11)
(12)
试中,
为孔隙度;
DT (μm/ft)为声波时差;
CNL (%)为补偿中子。
3.3.3. 预测结果
在分类对该区段全井储层孔隙度进行预测后,通过分析孔隙度值的分布区间,作如图4直方图。
从直方图可得出,I类储层孔隙度主要分布在8%以上,II类储层主要分布在4%~8%,III类储层主要分布在2%~4%,IV类储层主要分布在2%以下,预测效果良好。
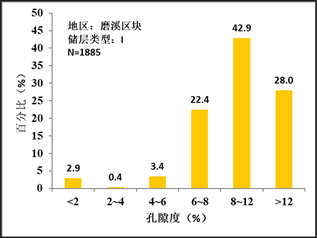
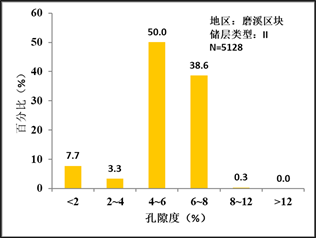
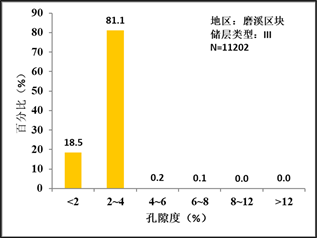
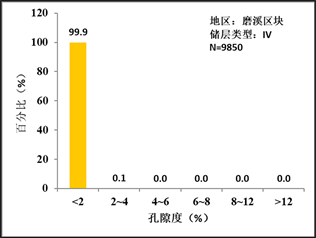
Figure 4. Predicted porosity distribution of each reservoir type
图4. 各储集类型预测孔隙度分布图
3.4. 预测效果
根据4类回归方程分别对4类储集类型的孔隙度进行预测,并将B井灯影组在Resform软件中成图,可以得到储层类型的测井解释图如图5所示。
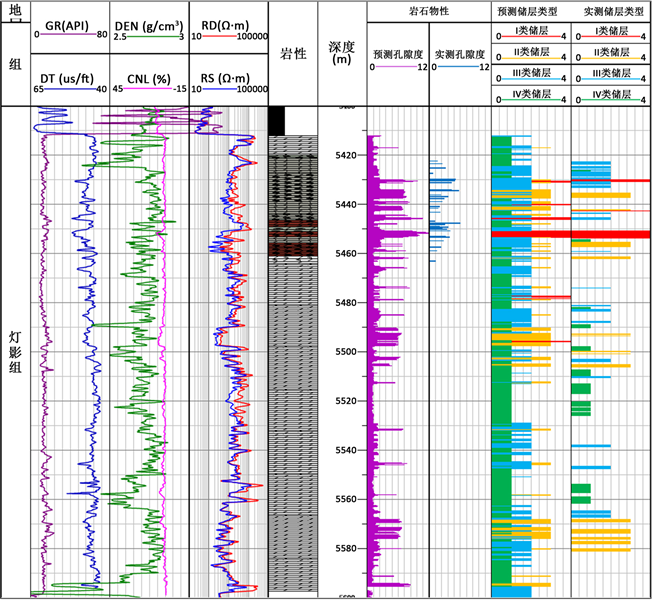
Figure 5. Reservoir type prediction map of Denger formation in well B
图5. B井灯二段储层类型预测图
4. 结论
1) 支持向量机具有显著的分类能力,在样本较少的情况下能够精确度较高地进行预测。
2) 定向多元线性回归在应对碳酸盐岩储层等非均质性极强的预测工作较实用,同时有效地解决了样本数据人工误差等问题。
3) 单只依照声波曲线值分布特征无法明确地划分II类储层与III类储层,还需进一步分析其他电性参数对划分II类储层与III类储层的贡献率。
4) 该预测方法建立在MATLAB 2018a软件编程基础上,结合Excel VBA进行统计分析绘图,全程自动化实现,将MATLAB数据处理功能与Excel的绘图功能相结合,实现统计分析绘图的自动化和批量化,将烦琐、机械的绘图工作解放出来,提高工作效率和质量。同时该程序操作简单灵活,实用性强。