1. 引言
地层结构是在漫长的地质历史演化过程中形成的,其时空分布具有不均匀、不规则等特点,在宏观上具有一定的统计规律 [1]。地层结构的识别有多种方法,其中钻探法是获取地层构造以及岩性分层详细分布信息最为直观、可靠的手段 [2];钻孔数据所记录的信息准确率高,是三维地质建模的重要依据 [3],也是地铁工程选线、设计和施工中必不可少的数据资料。在三维地质建模中连接各钻孔地层时,主要使用线性插值、多项式插值、反距离插值和kriging插值等空间插值方法,各种不同的插值方法得到的模拟结果存在一些差异,具有一定的局限性 [4]。
本文以南宁地铁1号线部分路段作为研究对象,由于线路要穿越人口稠密繁华商业区、市民居住区以及车流量较大的交通要道,勘察施工会给周围环境和市民生活带来影响 [5]。南宁地区可溶岩广泛分布,施工时很容易发生岩溶塌陷与突水事故 [6]。因此,在南宁地铁建设中,往往由于勘探场地受限,获取钻孔数据成本高,如何利用有限的钻孔数据识别地层岩性及其层序分布是值得关注和探索的问题。
近年来,机器学习算法得到了迅速发展,算法建模既可以用于大型复杂数据集,也可以在较小数据集上建立更准确的模型 [7],此方法在地质学领域得到不断推广和应用;陈玉林等 [8] 基于K近邻算法识别合水地区的岩性,分类准确率达到89.5%;郭甲腾等 [9] 基于支持向量机和BP神经网络实现钻孔数据自动地层分类,提出需进一步探索超参数的经验值确定方法;Cracknell等 [10] 基于地球物理数据对比研究了5种机器学习方法的地层分类效果,其中随机森林算法的分类效果最好;马梓程等 [11] 利用光谱和纹理信息,基于随机森林建立了火成岩分类模型;徐剑波和陈军林 [12] 应用随机森林算法结合区域的化探数据来推断地质体的空间分布。因此,在此基础上,本文提出了一种基于随机森林(Random Forest, RF)模型的钻孔数据地层识别方法,并与支持向量机(Support Vector Machine, SVM)模型进行对比分析。
2. 研究方法
2.1. 随机森林算法
随机森林是Bagging方法和Random子空间的组合 [13],基本构成单元是决策树,通过多棵决策树的组合提高分类的准确性。首先随机生成训练集,利用bootstrap方法随机为每棵树生成训练数据,可能重复包含,也可能不重复包含某些数据,并由此构建K棵分类决策树,每次未被抽到的样本组成袋外数据(Out-Of-Bag, OOB)。随机选择特征子集:当决策树节点拆分时,随机选择特征子集,该子集的大小m通常小于特征总数M。计算m个特征下的基尼系数,选择最佳分割特征。集合每棵决策树的预测结果,且每棵树被采样的机会均等,可以有效地生成随机树,并且将大量随机树组合在一起可以得出准确的模型,通过最终投票对未知类别的样本进行分类。
本文提出的基于随机森林的钻孔数据地层识别流程如图1所示。关键步骤包括:1) 对钻孔数据进行预处理,按地层类型划分样本并随机划分训练集和测试集;2) 利用训练集内部交叉验证寻找适合当前问题的随机森林模型超参数组合;3) 根据最优超参数,训练随机森林分类器;4) 由训练好的分类器对测试集进行预测分类,确定其地层类型。
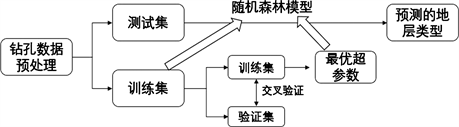
Figure 1. Process of strata recognition for borehole data based on Random Forests
图1.基于随机森林模型的钻孔数据地层识别流程
2.2. 地层分类树
本文以CART分类树 [14] 为基学习器构建RF地层识别模型。CART分类树为二叉分类树,由根节点、子节点和叶子节点组成,其中每个从根节点到叶子节点的路径都对应着其依据地层相关属性的分类过程,而叶子节点则对应一种地层类别。使用CART决策树进行节点分割时,选择具有最小基尼系数的特征作为最佳分割属性 [15],计算如下:
(1)
式中:Pi为地层类型i在t节点处的概率,Gini(t)为0时,表示在t节点处的样本数据为同一地层类型;Gini(t)越大,表明在t节点处的样本数据越趋于均匀,能获得的分类信息越少。
如图2所示,样本集S1的训练过程对应于CART分类树的生长过程,即把位于根节点的样本集S1按所给定的属性划分不断进行递归分割。单棵地层分类树的生长训练过程如下:
1) 利用bagging方法获取训练集。从具有N个样本的总训练集中有放回地随机抽取n个组成单棵树的训练集S1。
2) 随机选取节点的属性指标。在钻孔数据当中共有M个属性,随机地从M个指标中选取m个作为节点指标。

Figure 2. Single strata classification tree
图2. 单棵地层分类树
3) 节点的递归分割。对于每一个节点的钻孔属性指标都要遍历所有可能的分割方法,选择最小的基尼系数作为此节点的分割标准,对应的属性指标为最优的地层分类指标,然后按最优地层分类指标进行分割。如图2中数据集S4根据最优属性指标t3分为两个子数据集4和S5,其中4节点的基尼系数已经很小(通过设定的阈值判断),可认为该节点所有样本属于同一类别,即地层类别4,不用继续向下分割;而数据集S5则继续分割。
4) 然后将生成的多棵树组成RF,用RF对新的数据进行分类,分类结果按树分类器投票决定。
2.3. 模型评价
假定
表示被分类为j类的i类样本,k表示地层类别的数量,则分类准确率A以正确分类的样本数与总样本数N的比值来表示:
(2)
该指标是用来衡量分类器对于测试集的总体分类精度,总体分类精度越高说明算法的分类效果越好。除整体分类精度外,各单一地层分类准确率也十分重要,这里选用召回率R和精确度的综合指标F1来表达,R表示被正确分类的地层样本占所有实际为该地层的样本比例,P表示被正确分类的地层样本占所有预测为该地层的样本比例,F1是召回率R和查准率P的综合指标。随机森林模型的评价指标公式 [16] 如下:
(3)
(4)
(5)
RF在训练过程中每次的bootstrap抽样,N个地层数据中的每条数据未被抽中的概率为
,当N足够大时,
,即为袋外数据(Out Of Bag, OOB)。RF利用这部分数据进行内部误差
估计,产生OOB误差,为在RF中为测试集误差的无偏估计,可利用python的机器学习库Scikit-learn直接输出。有2个主要参数会影响RF的效率和性能 [17]:树的数量以及叶节点的最小样本数量,可以使用网格参数搜索的办法来确定其最优超参数。
为量化地层分类预测的可靠性,引入余量函数(Margin function) [18],定义为:
(6)
式中:
为示性函数,余量函数用于度量平均正确分类数超过平均错误分类数的程度,余量值越大,分类预测越可靠。随机森林的泛化误差 [18] 定义为:
(7)
式中:下标X,Y表示概率P覆盖X、Y空间。在RF当中,当决策树数量足够多时,
会趋于一个上界,RF算法不会过拟合(Overfitting) [19]。
3. 应用算例
3.1. 研究区概况和钻孔数据分析
研究区域位于南宁市中心城区,选取地铁1号线170个钻孔勘察资料进行研究,其钻孔点位主要位于白苍岭站、南宁火车站站、朝阳广场站、新民路站、民族广场站,地铁5号线和7号线也将穿过本研究区域。朝阳广场站规划成为地铁1、2、7号线三线换乘车站,也是南宁市已有规划中唯一一座三线换乘站。钻孔揭露的地层主要为杂填土、粉土、泥岩、粉砂岩、砾石、黏土、粉砂共7类,统计的对应地层样本数量分别为124、75、221、101、131、180、68,总共900个样本。
首先将钻孔数据按钻孔编号整理,然后根据地层类型的不同,划分为不同的样本,表1为随机选取的2个钻孔数据及揭露的部分地层,展示了相关特征属性。钻孔剖面图如图3所示,训练中涉及的属性值包括钻孔位置坐标,每个地层分界点的起始深度、终止深度、层厚、钻孔地面标高。

Table 1. Drilling data and feature attributes
表1. 钻孔数据及特征属性
数据样本中钻孔坐标和土层厚度数量级差异很大,为了提高分类器的学习能力,对每个输入特征值进行标准化 [20],将处理后的输入数据标准化为零均值和单位方差,转化函数为
(8)
式中:
为标准化后的值;X为待标准化的值;
为样本数据的均值;
为样本数据的方差。
3.2. 超参数的敏感性分析
机器学习方法中,对于不同的建模数据,超参数难以确定唯一值,而不同的超参数组合会对建模结果产生很大影响。RF的性能主要受树的数量以及最小叶子节点数的影响,而SVM的性能则受到惩罚因子C和RBF核函数参数gamma这2个超参数的影响 [21]。因此,需要研究RF和SVM模型的超参数选取对建模准确率的影响。RF与SVM模型的超参数敏感性分析结果如图4所示。在机器学习中,常采用交叉验证分析超参数的敏感性 [22],为方便比较,统一采用5折交叉验证和网格搜索方法计算分析不同参数设置下模型分类准确率,结果显示RF分类器整体表现更好,且具备较低的超参数敏感性。图4(a)显示RF的两个重要超参数树的数量以及最小叶子节点数变化时,分类准确率的波动很小,图4(b)和图4(c)中RF的2个参数敏感性曲线都很平滑,不存在过拟合(over-fitting)与欠拟合(under-fitting)情况,测试集的波动范围相比于整体准确率而言很小,体现了模型分类的稳定性。图4(d)、图4(e)、图4(f)结果表明,SVM的参数非常敏感,波动范围很大,甚至会出现训练集和测试集结果相背离的情形,需要重点调整优化关键参数。图4(e)结果还表明,当C值设置不当时,总体精度只有大约20%。同时, 值设置对分类性能也有明显影响(见图4(f))。在实际应用中,使用粗网格搜索可能难于选定最优SVM参数,而使用精细网格进行计算,无疑会加大计算工作量。
3.3. 地层识别结果分析
为验证建模准确率,按照4:1划分训练集与测试集,即随机选择180个地层数据(占全部地层数据的20%)作为测试集用以评判建模结果,利用Scikit-learn机器学习包中的网格搜索进行模型参数调优 [23],混淆矩阵分析方法是评价模型性能好坏最直接有效的方法 [24]。图5和图6以混淆矩阵形式分别给出RF和SVM的分类预测结果。通过对比发现,2种模型都具有较好的分类能力,但RF模型在不同地层的分

Figure 4. Hyperparameter sensitivity map of Random Forest (a)~(c) and Support Vector Machine (d)~(f) under 5-fold cross-validation.
图4. RF(a)~(c)和SVM (d)~(f)在5折交叉验证下的超参数敏感性图
类结果几乎均强于SVM模型。表2给出了利用公式(2)、(3)、(4)、(5)得到的模型整体精度、综合指标F1值以及5折交叉验证得到的结果,随机森林模型3项指标分别为0.817、0.816和0.824,均略高于SVM,另外,RF的OOB值为0.824,具备较好的泛化性能。
为应对实际工程中钻孔数据样本有限的问题,此处验证RF对样本量的鲁棒性,随机选择不同数量样本,因需要验证在样本数量较少时的模型性能,所以此处按7:3划分样本集进行模型训练测试,以减
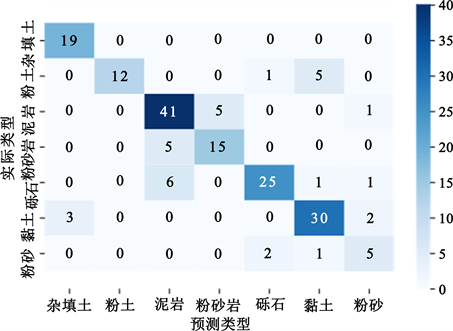
Figure 5. Confusion matrix of the RF classifier
图5. RF分类器分类结果的混淆矩阵

Figure 6. Confusion matrix of the SVM classifier
图6. SVM分类器分类结果的混淆矩阵

Table 2. Classification results of RF and SVM classifiers
表2. RF与SVM模型的分类结果
小测试误差。图7是不同样本数量下的测试集分类结果。由图7(a)可知,RF运行100次后获得的平均精度随样本数量的增加而增加,图7(b)显示标准差则会随之减小。样本数量由100增至900时,平均精度增加约20%,标准偏差下降约0.05。计算结果表明RF对于样本集数量的标准差稳定性较好,样本数量为300以上时,其准确率就达到70%以上,基本可以满足实际工程的需求。
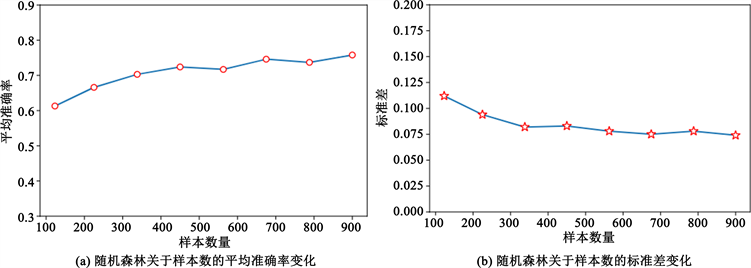
Figure 7. Mean accuracy and its standard deviation (RF runs 1000 times) versus the number of samples
图7. 随机森林随机划分1000次数据集,平均准确度及其标准偏差与样本数的关系
4. 结语
本文以南宁市地铁1号线的钻孔勘探资料为研究基础,提出了基于钻孔数据的随机森林地层分类方法,比较分析了随机森林和支持向量机2种机器学习算法在地层岩性分类中的应用,得出以下主要结论:
1) 分类模型评价指标为总体准确率和综合指标F1值,随机森林的准确率达到81.7%,F1值为0.816,不论是整体的分类能力还是各个地层的分类能力随机森林均强于支持向量机,它们的交叉验证结果也在0.8以上,保证了其泛化能力,同时随机森林在实际应用当中还可以不用划分测试集,用OOB误差精准便捷地评价其泛化能力。
2) 在超参数敏感性方面,与支持向量机比较,随机森林的参数敏感性更低,这在实际应用中会更加便捷、快速。与此同时,随机森林模型对于样本集数量的要求低,在低样本数量时得到的地层预测准确率和标准差良好。
3) 随机森林模型在利用钻孔数据识别地层方面具有明显的优越性,可以有效解决城市区域岩土工程勘探钻孔有限、稀疏的问题,对后续南宁地铁工程建设具有一定指导意义。
基金项目
国家重点研发计划资助项目(2017YFC0803300),南宁市科技局重点研发项目(02902530072)。
NOTES
*通讯作者。