1. 引言
在科学研究领域,偏振光已作为一门独立的光学学科。在生物、化学、医疗领域有着广泛的应用。一个普通的发光体是由大量的发光原子或分子组成的,每个发光原子每次发射一个持续时间为微秒级或更短的近似平面波的波列,每一个原子或分子都是一个随机的自发辐射过程,彼此没有联系,从而导致合成的振动方向光场矢量各不相同,相关时间大大缩短了。光波在介质的表面上发生了反射、透射或是散射时,其偏振态的改变与物质自身的性质有关,如目标的表面结构,材料属性等。光在物体内部传输时,在一些物体外部施加磁场、应力时,也会出现不同的偏振态形式。偏振态能够提供比非偏振技术更丰富的信息。根据光波偏振特性来研究目标识别的偏振特性,最初是应用于天体表面物质特性研究和空间天体探测方面,在天体物理学中,空间被测目标也有一定偏振特性。因此,偏振态可以识别目标的位置和材料属性,偏振遥感成像与分析技术已应用于大气和云层中溶胶状态的探测、资源调查等领域 [1]。对生物组织病变前后反馈的光偏振参数进行对比和分析,可以快速、准确的给病理信息。在医疗诊断方面,圆偏振光的传播方式和螺旋型的蛋白质等分子结构相吻合,透过人体时吸收效果较好,光偏振检测技术在影像处理方面也有应用 [2] [3] [4],对偏振参数和光谱参数进行融合计算,在恶劣的环境下可以增强图像边缘信息,了解探测目标散射特点后,被侦查目标可以通过雷达识别,可最大限度的对敌方军事目标进行毁伤,并对敌方更有效的军事打击 [5] [6]。2010年,吕鑫,蒋卓勤 [7] 等人在现有的方案上推导出了新的斯托克斯计算公式,提出了一种能对高速变化的偏振态进行实时测量的新方案。近几年来,随着激光技术的发展,光学的应用产品越来越多,其中偏振光作为一种重要的测量手段更受人们的欢迎 [8] [9] [10],可以在复杂的背景环境中检测出实用的信息。通过高速偏振态测量系统的理论计算,偏振态探测技术的研究对光通信、光传感等领域,有着重要的指导意义。
2. 理论计算
如果用偏振态测量装置测量自然景物反射光的偏振特性时,假设进入测量系统的光子集合表示为:
(1)
其中
表示状态为
(2)
为总的光子数量,其中
和
分别表示沿x轴和y轴的单位矢量,并且
。
在大多数偏振文献中,实现偏振态测量的方案很多,图1~图4为一种典型的偏振态测量方法 [11]。

Figure 1. Principle of measuring polarization state
图1. 测量偏振态原理
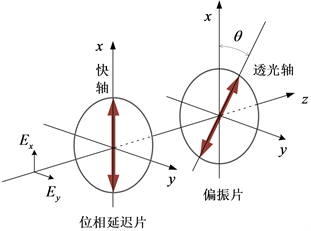
Figure 2. The orientation of the device (the third channel has a wave plate)
图2. 器件的方位(第3通道有波片)
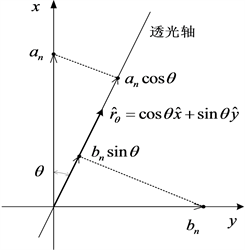
Figure 3. Amplitude of light transmitted by polarizer
图3. 偏振片透射光的振幅
图1的四路输出测量系统的分光器是等光强分束器、并且偏振无关(保偏分束器),因此入射光子经过分束器后,光子的状态保持原有的信息,对于四路分束器来讲,根据归一化要求,可得到各路光子状态的归一化系数为0.5。对于
状态的光子,在分束器各路的状态可以表示为:
(3)

Figure 4. θ Unit vector decomposition of direction
图4. θ方向的单位矢量分解
在图1的偏振测量装置中,根据(3)式,可得第1路光强为:
(4)
当测量系统入射的光子数为
时,则第1路的光强为:
(5)
在第2路偏振片之后,光子状态为:
(6)
则第二路的光强为:
(7)
入射
状态的光子数为
时,则第2路的光强为:
(8)
对于第3路,根据偏振片透光轴与x轴夹角为
,可得到偏振片后的光子状态为:
(9)
在(9)式中,
表示沿偏振片透光轴方向的单位矢量,其表达式为
(10)
当第3路的偏振片方位角
时,透过偏振片的光子状态为:
(11)
第3路偏振片后的光强为:
(12)
在(12)式中
。
当入射光子数为
时,则偏振片后光强为:
(13)
对于第4路,波片后的光子状态为:
(14)
可得到偏振片后的光子状态为:
(15)
当第4路的偏振片方位角
时,偏振片后的光子状态为:
(16)
此时光强为:
(17)
当入射光子数为
时,则加偏振片后光强为:
(18)
因为所有的光子状态相同,通过
、
、
和
的结果得出光子集合态的斯托克斯参量。并给出每个斯托克斯参量的计算公式。
(19)
(20)
(21)
(22)
3. 光子集合与Stokes关系
如果进入偏振光测量系统的光子集合为
的情况时,各光探测器输出电流分别为:
(23)
(24)
(25)
(26)
(22)式至(25)式探测器输出信号
、
、
和
为光子集合的贡献。此时系统给出的斯托克斯参量为
(27)
(28)
(29)
(30)
由于系统输入的是光子集合,无法利用(26)~(29)结果得出集合中光子的斯托克斯参量。
4. 结论
根据以上推导分析,可分两种情况进行解释不同集合光子的偏振态的叠加。假设第一种情况是
个
状态的光子和
个
状态的光子,利用(26)-(29)式得出斯托克斯参量为:
(31)
(32)
(33)
(34)
如第二种情况是
个
状态的光子和
个
状态的光子,利用(26)~(29)式得出斯托克斯参量为:
(35)
(36)
(37)
(38)
针对光学偏振态的测试需求,对光子集合偏振态的理论研究,推导出光子集合与斯托克斯矢量的关系以及相应的计算公式,得到光子集合偏振态的斯托克斯四个矢量参数,如果适当选择
、
、
、
这些参数,可以使得
、
、
和
。虽然光子集合偏振态的构成有所不同,但是测量装置给出的结果却是相同的,这就是目前偏振态测量装置的特性。理论推导出光子集合偏振态与斯托克斯矢量的函数关系,对今后的偏振态测量技术有一定的指导意义。
NOTES
*通讯作者。