舰艇纵倾平衡系统水锤冲击激振特性分析

Analysis of Vibration Characteristics Induced by Water Hammer of Ship’s Longitudinal Inclination and Balance System

摘要: 舰艇水下航行过程中需频繁进行纵倾平衡水舱的移水操作，经常出现水锤现象，从而诱发系统高强度瞬态振动及瞬态噪声，通过FLOWMASTER输出瞬态载荷力，并在CAESAR II中建立纵倾移水系统模型，进行时间历程分析计算。同时，计算分析了支撑高度、支撑刚度、固定方式和支撑间隔对舰艇纵倾平衡系统振动的影响，为后续管路系统的三维设计提供支撑。

Abstract: In the process of underwater navigation, it is necessary to move water in the longitudinal inclina-tion and balance tank frequently. Water hammer often occurs, which induces high-intensity tran-sient vibration and transient noise of the system. The transient load force is output through Flow Master, and the model of water transfer system is established in CAESAR II for time history analysis and calculation. At the same time, the influence of support height, support stiffness, fixing mode and support spacing on the vibration of longitudinal inclination and balance system is calculated and analyzed, which provides support for the subsequent three-dimensional design of pipeline system.

1. 引言

舰艇纵倾移水系统的功能是通过艏、艉平衡水舱间的移水，改变艏、艉液舱的动载荷重量，消除纵倾力矩差，实现纵倾姿态的调整。舰艇水下航行过程中需频繁进行纵倾平衡水舱的移水操作，经常出现水锤现象。水锤引起的冲击激振十分剧烈，水锤问题 [1] [2] [3] 是诱发系统高强度瞬态振动及瞬态噪声的主要原因。因此，需对本系统进行水锤冲击振动的仿真计算。

输流管道，系统操作会诱发水力暂态过程，严重时产生水锤的极端水力现象。作为一种极端的非定常流动问题，水锤产生的压力升高以波的形式在管道系统中运动，从而造成了在管道中同时并存有流体运动、压力波动以及管道振动等多种运动的形式，这些具有不同特性的运动形式之间的耦合作用称为流体与结构之间的耦合(Fluid Structure Interaction)，或简称为流固耦合(FSI)。

通常对管道系统耦合动力学分析 [4] [5] 的主要方法有：特征线方法(The Method of Characteristics, MOC)、有限元法(Finite Element Method, FEM)和传递矩阵法(Transfer Matrix Method, TMM)、行波法(The Traveling Wave Method)。

其中有限单元法是将连续的求解域离散为一组有限个单元的组合，这样的组合体能解析地模拟或逼近求解区域。在流固耦合过程中，流体与固体两相介质交互作用，其非线性特性是非常明显的。不仅流体运动方程是非线性的，而且耦合运动的特性将随着结构振动的幅值不同而变化，这就使得耦合过程的力学行为呈现出十分复杂的特征，其数学描述是高度非线性的。与其它方法相比，有限元方法具有对复杂边界条件和几何形状良好适应性和更容易处理复杂本构关系和非线性问题的优点，因此它能够灵活地模拟和逼近复杂的求解区域。

2. 水锤基本理论与数学模型

在有压管道中，当流体的流速因为某种原因发生突然改变时，由于流体的动能和压能相互转换，流体会对阀门、管壁等水力部件产生一个压力，而管壁摩擦损失一般较低，在惯性的作用下，后续流体会使得压力迅速达到最大，从而在管道内引起可能会破坏管路的水击现象。引起管道中产生水锤现象的诱因有很多，比如水泵开启或突然失电，阀门的突然启闭等。因此需要对纵倾平衡系统的过渡过程进行分析研究，特别是压力波在管道中的传播过程。水锤波在有压管道中的传播过程较为复杂。在流体的压缩性和惯性、管道弹性和阻力的共同作用下，水锤波会在管路中以多种形式来回传播，如叠加、干涉、反射，直至水锤波消散达到稳定。所以主要利用特征线法对纵倾平衡系统的水力过渡过程进行计算，这里主要介绍相关的基本理论和公式推导。

2.1. 水锤基本方程

水锤基本方程包含两个方程：运动方程和连续性方程。运动方程是基于流体的动量守恒定律，连续性方程是基于流体的质量守恒定律。

2.1.1. 运动方程

如图1所示，假设有一团微小流体，长度为 $\Delta x$，横截面积为A，离基准线高度为Z，压力为H，且流体的原始运动方向与x坐标轴的正方向相反，管道与水平基准线的夹角为水锤发生点为 $\alpha$，直径为D，摩擦应力为τ₀，水锤发生在坐标原点。

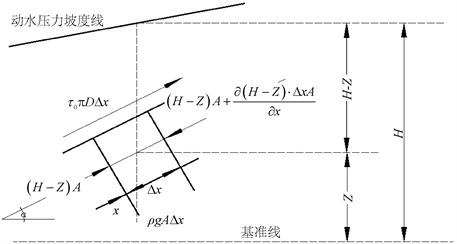
Figure 1. Forces on small water bodies

图1. 微小水体上的作用力

对微小水体进行受力分析，其受到上下表面的压力，管道的摩擦力和重力的作用，根据牛顿第二定律：

$-\frac{\partial \left(H-Z\right)\cdot \Delta xA}{\partial x}-\rho g\Delta x\sin \alpha -{\tau }_0\pi D\Delta x=\rho A\Delta x\frac{\text{d}V}{\text{d}t}$ (2.1)

由于：

$\frac{\text{d}V}{\text{d}t}=\frac{\partial V}{\partial t}+\frac{\partial V}{\partial x}\frac{\partial x}{\partial t}=\frac{\partial V}{\partial t}+V\frac{\partial V}{\partial x}$ (2.2)

可将式2.1化简为：

$g\frac{\partial H}{\partial x}+V\frac{\partial V}{\partial x}+\frac{\partial V}{\partial t}+\frac{4{\tau }_0}{\rho D}=0$ (2.3)

切应力τ₀的值在速度为定常时是不变的，按照Darcy-Weisbach公式，即得到：

${\tau }_0=\frac{1}{8}\rho f{V}^2$ (2.4)

式中f为摩阻系数。将式2.4代入式2.3中即可得：

$\frac{\partial H}{\partial x}+\frac{V}{g}\frac{\partial V}{\partial x}+\frac{1}{g}\frac{\partial V}{\partial t}+\frac{fV}{2gD}\left|V\right|=0$ (2.5)

式2.5被称为水锤运动方程。

2.1.2. 连续性方程

仍利用图1，根据质量守恒定律：dt时段内流入与流出控制体的流体质量差等于同一时段此控制体流体质量的变化量，即：

$-\frac{\partial }{\partial x}\left(\rho AV\text{d}t\right)\text{d}x=\frac{\partial }{\partial t}\left(\rho A\text{d}x\right)\text{d}t$ (2.6)

整理得：

$\frac{\partial \left(\rho A\right)}{\partial t}+\frac{\partial \left(\rho AV\right)}{\partial x}=0$ (2.7)

在产生水锤时，流体断面积A、流体密度 $\rho$ 、以及截面平均流速V都是关于x和t的函数，可对式2.7化简整理为：

$-\frac{\partial V}{\partial x}=\frac{1}{A}\frac{\text{d}A}{\text{d}t}+\frac{1}{\rho }\frac{\text{d}\rho }{\text{d}t}$ (2.8)

将式2.8继续简化可得：

$\frac{\partial H}{\partial t}+V\frac{\partial H}{\partial x}+\frac{a^2}{g}\frac{\partial V}{\partial x}=0$ (2.9)

式中：H——管道中流体的压力水头(m)；

V——管道中流体的流速(m/s)；

$\alpha$ ——水锤波波速(m/s)。

一般而言：

$\frac{\partial H}{\partial x}\ll \frac{\partial H}{\partial t}$ (2.10)

所以式2.9可以继续化简为：

$\frac{\partial H}{\partial t}+\frac{a^2}{g}\frac{\partial V}{\partial x}=0$ (2.11)

式2.9和2.11均为水锤的连续性方程。

3. 系统建模

纵倾移水系统包含直管、弯管、阀门以及支承架等主要元件。计算结果精确度的关键在于合理地确定力学模型中每个元件的弹性与惯性性质。

为了保证模型的准确性，建模时遵守以下原则：凡是由地面支承的管线，无论覆土与否，直径大于300 mm的管道，节点之间的距离小于等于20倍的管道直径；而对于直径小于等于300 mm的管道，节点之间的距离不大于30倍管道直径。对于有管架约束的管道，管段节点均划分在管架处，否则管架间的节点将因为重量无承载而产生错误的纵向位移。

对于建立的模型进行分析、比对和调整，保证建立模型的准确，并且确保各管路运行的安全与稳定。整体系统模型如图2所示，其中阀门与法兰模型如图3所示。

Figure 2. Overall system model

图2. 系统整体模型

Figure 3. Flange—valve model

图3. 法兰——阀门模型

4. 纵倾移水系统水锤激振时间历程分析

首先运用FLOWMASTER输出瞬态载荷力，得到不同时刻下的各管段水锤力数值。进而在CAESAR II中建立纵倾移水系统模型，进行模态分析，确定系统的固有频率与模态振型。将FLOWMASTER中得到的水锤力输入到计算模型中，并设置水锤力方向，进行工况组合，完成时间历程计算。

针对不同移水方向、移水压力、阀门启闭时间，选取了移水压力0.8 MPa，移水方向艏向艉，关阀时间1 s的工况，此次重点关注球阀前后法兰与支架的振动情况，将阀前法兰、阀后法兰、阀前支撑、阀后支撑四处节点各时刻、各方向的位移数据分别输出。CAESAR II原始计算结果如图4所示，此时阀前支撑、法兰位移如下表1左侧两栏，阀后冲击峰值压力为4.87 MPa，此时阀后支撑、法兰位移为右侧两栏。阀门处水锤荷载和重力荷载共同作用下的位移变形和应力云图如图5~8所示。

Table 1. Displacement under maximum impact pressure

表1. 受最大冲击压力时位移

5. 管系振动影响因素研究

5.1. 支撑高度

以移水压力0.8 MPa，艏向艉移水，1 s关阀的工况为例，分别取支撑高度为520 mm、1020 mm (实际高度)、1520 mm的三种情况，计算阀前支撑、阀前法兰、阀后法兰、阀后支撑最大位移的大小，结果如下表2~4。由计算结果可见，支撑高度对管系振动存在影响，支撑越高，管系振动越大。

Figure 4. Original calculation results

图4. 原始计算结果

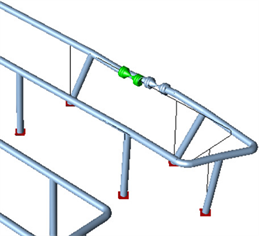
Figure 5. Peak vibration displacement deformation of water hammer in front of valve

图5. 阀前水锤峰值振动位移变形

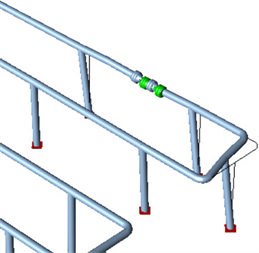
Figure 6. Peak vibration displacement deformation of water hammer behind valve

图6. 阀后水锤峰值振动位移变形

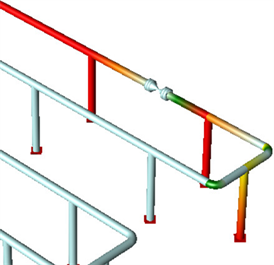
Figure 7. Cloud chart of peak stress of water hammer in front of valve

图7. 阀前水锤峰值应力云图

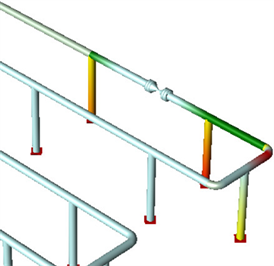
Figure 8. Cloud chart of peak stress of water hammer behind valve

图8. 阀后水锤峰值应力云图

Table 2. Maximum displacement of flange and support near valve at 520 mm height

表2. 高度520 mm下阀门附近法兰、支撑最大位移

Table 3. Maximum displacement of flange and support near valve at 1020 mm height

表3. 高度1020 mm下阀门附近法兰、支撑最大位移

Table 4. Maximum displacement of flange and support near valve at 1520 mm height

表4. 高度1520 mm下阀门附近法兰、支撑最大位移

5.2. 支撑刚度

以移水压力0.8 MPa，艏向艉移水，1 s关阀的工况为例，分别取支撑刚度为1000 N/cm、2500 N/cm (实际刚度)、5000 N/cm、10000 N/cm的情况，计算阀前支撑、阀前法兰、阀后法兰、阀后支撑最大位移的大小，结果如下表5~8。可见支撑刚度越大，则管系的振动越小。

Table 5. Maximum displacement of flange and support near valve under 1000 N/cm stiffness

表5. 刚度1000 N/cm下阀门附近法兰、支撑最大位移

Table 6. Maximum displacement of flange and support near valve under 2500 N/cm stiffness

表6. 刚度2500 N/cm下阀门附近法兰、支撑最大位移

Table 7. Maximum displacement of flange and support near valve under 5000 N/cm stiffness

表7. 刚度5000 N/cm下阀门附近法兰、支撑最大位移

Table 8. Maximum displacement of flange and support near valve under 10000 N/cm stiffness

表8. 刚度10000 N/cm下阀门附近法兰、支撑最大位移

5.3. 固定方式

纵倾移水系统中，管道支撑均采用刚性管夹连接，限制管道的径向振动与竖直方向振动，对应CAESAR II模型中Y方向与Z方向。以移水压力0.8 MPa，艏向艉移水，1 s关阀的工况为例，将管夹改为固定支撑，限制轴向、径向与竖直方向位移，计算阀前支撑、阀前法兰、阀后法兰、阀后支撑最大位移的大小，与原固定方式形成对比，结果如下表9~10。可见采取固定支撑后，管系振动减小。

Table 9. Maximum displacement of flange and support near the valve when fixed support is adopted

表9. 采取固定支撑时阀门附近法兰、支撑最大位移

Table 10. Maximum displacement of flange and support near valve when original support is adopted

表10. 采取原有支撑时阀门附近法兰、支撑最大位移

5.4. 支撑间隔

将DN80管段支撑间隔由2 m改为4 m，以移水压力0.8 MPa，艏向艉移水，1 s关阀的工况为例。计算阀前支撑、阀前法兰、阀后法兰、阀后支撑最大位移的大小，与原支撑间隔形成对比，结果如下表11~12。可见支撑间隔越大，管系振动幅度越大。

Table 11. Maximum displacement of flange and support near valve with support interval of 4 m

表11. 支撑间隔4 m时阀门附近法兰、支撑最大位移

Table 12. Maximum displacement of flange and support near valve when original support is adopted

表12. 采取原有支撑时阀门附近法兰、支撑最大位移

6. 小结

支撑高度、支撑刚度、固定方式和支撑间隔都会对舰艇纵倾平衡系统的振动产生影响。通过建模，并进行水锤激振时间历程分析得知，支撑越高、支撑间隔越大或支撑刚度越小，管系振动则越大。采取固定支撑后，管系振动则会减小。