基于事件触发脉冲控制的变时滞系统稳定性研究

Stability Analysis of Time-Varying Delay Systems Based on Event-Triggered Impulsive Control

摘要: 本文研究了事件触发脉冲控制下变时滞系统的稳定性问题。首先我们设计了一种由系统状态决定脉冲作用时刻的事件触发脉冲控制，证明了系统不存在Zeno现象。其次我们得到了变时滞系统在提出的事件触发脉冲控制下指数稳定的充分条件。最后仿真实验结果验证了理论方案的有效性。

Abstract: This paper investigates the stability of time-varying delay systems via an event-triggered impulsive control. Firstly, the event-triggered impulsive control is designed where the impulsive instants are determined by the system states, and Zeno-behavior is ruled out. In addition, sufficient conditions of exponential stability of time-varying delay systems are gained under the proposed event-triggered impulsive control. A numerical example is finally given to illustrate the effectiveness of the theoretical results.

1. 引言

近几十年来，非线性系统在工程、生物等各领域展现出巨大的应用潜力，其稳定性问题一直是学者们关注的焦点。在实际应用中，许多非线性系统如Mackey-Glass模型 [1] 和蔡氏电路系统 [2] 中存在的时滞可能导致不稳定、振荡和混沌等复杂的动力学行为 [3]。为了使非线性时滞系统达到稳定，目前大多采用状态反馈控制 [4]、牵引控制 [5]、自适应控制 [6] 等控制方法。

上述连续或分段连续控制方法虽然能保证系统控制性能，但是控制成本高。此外，在某些情况下如卫星轨道转换系统 [7] 无法接受连续控制。因此，作为一种只在某些时刻输入到系统中的离散控制方法，脉冲控制被广泛应用于各个领域 [8] [9]。Yang等 [10] 将脉冲控制应用到非线性时滞系统中，并给出了脉冲控制下非线性时滞系统指数稳定的充分条件。Tang等 [11] 基于脉冲控制方法分析了一类参数不匹配的领导跟随系统的有界同步行为。Guan等 [12] 研究了分布式脉冲控制下两种不同类型时滞的复杂动态网络的同步问题。由于在网络系统中控制每个节点的成本高，Sun等 [13] [14] 基于脉冲牵引控制讨论了强连通、非强连通网络和混杂网络的同步问题。

在脉冲控制中脉冲作用时刻是由时间决定的，也就是说，所有的采样点是按照时间周期提前设置好的，与系统状态无关，这可能会导致通信带宽、计算资源的浪费。事件触发控制是由系统状态决定的，只有当系统状态误差超过规定的阈值时才执行 [15]。由于它能有效弥补脉冲控制按周期触发的不足，提高资源利用率而受到学者们的广泛关注。Dimarogonas等 [16] 研究了集中式事件触发和分散式事件触发控制下多智能体系统的一致性问题，并证明了多智能体系统在两种事件触发控制下都不存在Zeno现象。Lu等 [17] 基于两种不同的事件触发控制讨论了耦合动力系统的同步问题。

近年来，事件触发控制和脉冲控制相结合形成的事件触发脉冲控制是控制领域研究的热点之一。其脉冲时刻是由一些与系统状态相关的条件决定的，在一定程度上减少了数据采样次数，这一优势使得相关研究不断增加。Zhu等 [18] 讨论了事件触发脉冲控制下线性、非线性动力系统的稳定性问题，以及主从记忆网络系统的同步问题。Sun等 [19] 研究了事件触发脉冲控制下异构网络系统的有界同步问题。目前这些研究成果建立在没有时滞的理想状态下，然而，在实际应用过程中由于信息传递速度、通信时间有限等因素，时滞是不可避免的 [20] [21] [22]。因此，本文在已有工作的基础上，研究了变时滞系统在事件触发脉冲控制下的稳定性问题，证明了系统不存在Zeno现象。此外，我们得到了变时滞系统在提出的事件触发脉冲控制下指数稳定的充分条件。最后，数值仿真验证了理论方案的有效性。

2. 问题描述及预备知识

考虑以下非线性变时滞微分方程：

$\stackrel{\dot{}}{x}\left(t\right)=-Cx\left(t\right)+Af\left(x\left(t\right)\right)+Bg\left(x\left(t-\tau \left(t\right)\right)\right)+U\left(t\right)$ (1)

式中 $x\left(t\right)={\left(x_1\left(t\right),\cdots ,x_n\left(t\right)\right)}^{\text{T}}\in R^n$ 是方程的状态向量，对角矩阵 $C=diag\left(c_1,\cdots ,c_n\right)$ 为正定矩阵，A，B为 $n\times n$ 阶常数矩阵。非线性函数 $f\left(x\left(t\right)\right)={\left(f_1\left(x\left(t\right)\right),\cdots ,f_n\left(x\left(t\right)\right)\right)}^{\text{T}}$， $g\left(x\left(t\right)\right)={\left(g_1\left(x\left(t\right)\right),\cdots ,g_n\left(x\left(t\right)\right)\right)}^{\text{T}}$ 为连续可微函数且 $f\left(0\right)=g\left(0\right)=0$。 $\tau \left(t\right)$ 为有界变时滞函数，即 $0\le \tau \left(t\right)\le \tau$。时滞系统初值函数 $\psi \left(s\right)={\left[{\psi }_1\left(s\right),\cdots ,{\psi }_n\left(s\right)\right]}^{\text{T}}\in C\left(\left[-\tau ,0\right],R^n\right)$，其中 $C\left(\left[-\tau ,0\right],R^n\right)$ 是从 $\left[-\tau ,0\right]$ 到 $R^n$ 的连续映射。 $U\left(t\right)$ 为控制输入。

为了减少数据采样次数，提高资源利用率，本文采用以下事件触发脉冲控制：

$U\left(t\right)={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\left[Kx\left(t_k\right)-Lx\left(t\right)\delta \left(t-t_k\right)\right]}$ (2)

式中K，L为增益矩阵， $\delta (\cdot )$ 表示Dirac函数， $x\left(t_k\right)\ne 0$，事件触发脉冲时刻 ${\left\{t_k\right\}}_{k=1}^{\infty }$ 满足 $0=t_0<t_1<\cdots <t_k<\cdots ,{\lim }_{k\to \infty }{t}_k=\infty$。

因此，在控制(2)的作用下，(1)式可以转化为：

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=-Cx\left(t\right)+Af\left(x\left(t\right)\right)+Bg\left(x\left(t-\tau \left(t\right)\right)\right)+Kx\left(t_k\right),\\ \Delta x\left(t_k\right)=-Lx\left(t_k\right),t=t_k\end{array}$ (3)

其中 $\Delta x\left(t_k\right)=x\left(t_k^{+}\right)-x\left(t_k^{-}\right)$ 且 $x\left(t_k^{+}\right)={\lim }_{h\to 0^{+}}x\left(t_k+h\right)$， $x\left(t_k\right)=x\left(t_k^{-}\right)={\lim }_{h\to 0^{-}}x\left(t_k+h\right)$。定义变时滞方程(3)的测量误差为 $e\left(t\right)=x\left(t_k\right)-x\left(t\right)$，I为单位矩阵，则(3)式可以进一步表示为：

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=-Cx\left(t\right)+Af\left(x\left(t\right)\right)+Bg\left(x\left(t-\tau \left(t\right)\right)\right)+K\left(e\left(t\right)+x\left(t\right)\right)\\ x\left(t_k^{+}\right)=\left(I-L\right)x\left(t_k\right),t=t_k.\end{array}$ (4)

为了研究变时滞微分方程(1)的稳定性，本文给出以下假设、引理和定义：

假设1 [11] 对 $\forall z_1,z_2\in R^n$ 非线性函数 $f(\cdot ),g(\cdot )$ 满足Lipschitz条件：

$\Vert f\left(z_1\right)-f\left(z_2\right)\Vert \le u_1\Vert z_1-z_2\Vert ,\Vert g\left(z_1\right)-g\left(z_2\right)\Vert \le u_2\Vert z_1-z_2\Vert ,$

$u_1,u_2>0$ 为Lipschitz常数。

假设2 [11] 假设 $x\left(t\right)$ 有界，即对于任意的初值 $\psi \left(s\right)$， $-\tau \le s\le 0$，存在正数 $d>0$， $T>0$ 使得对每一个 $t\ge T$ 有 $\Vert x\left(t\right)\Vert \le d$。

引理1 [20] 若 $\gamma >0$，则对任意 $x,y\in R^n$ 以及 $n\times n$ 阶矩阵A，不等式

$2x^{\text{T}}Ay\le \gamma x^{\text{T}}A{A}^{\text{T}}x+\frac{1}{\gamma }{y}^{\text{T}}y$

成立。

引理2 [10] 令 $PC=\left\{\phi |\phi :\left[-\tau ,\infty \right)\to R\right\}$，假设存在常数m，n，p使得 $\mu \left(t\right),\vartheta \left(t\right)\in PC$ 满足：

$\{\begin{array}{l}{D}^{+}\mu \left(t\right)\le -m\mu \left(t\right)+n\mu \left(t-\tau \left(t\right)\right),t\ne t_k\\ \mu \left(t_k^{+}\right)\le p\mu \left(t_k\right),k=1,2,\cdots \end{array}$

且

$\{\begin{array}{l}{D}^{+}\vartheta \left(t\right)>-m\vartheta \left(t\right)+n\vartheta \left(t-\tau \left(t\right)\right),t\ne t_k\\ \vartheta \left(t_k^{+}\right)=p\vartheta \left(t_k\right),k=1,2,\cdots \end{array}$

若 $-\tau \le t\le 0$ 时 $\mu \left(t\right)\le \vartheta \left(t\right)$，则当 $t>0$ 时仍有 $\mu \left(t\right)\le \vartheta \left(t\right)$ 成立，其中 $D^{+}\mu \left(t\right)=\lim {\sup }_{h\to 0^{+}}\frac{\mu \left(t+h\right)-\mu \left(t\right)}{h}$。

定义1 [18] 若存在常数 ${\rho }_1$ 使得

${\rho }_{\text{1}}=\inf \left\{t_{k+1}-t_k\right\}>0,$

则系统(1)在事件触发脉冲控制(2)下不存在Zeno现象，即事件触发脉冲控制在有限时间段内不会无限次采样。

定义2 [10] 对于事件触发脉冲控制(2)下的系统(1)，若存在常数 $M>0$， $\lambda >0$ 使得系统(1)的解 $x\left(t\right)$ 满足：

$\Vert x\left(t\right)\Vert \le M\Vert \psi \Vert \exp \left(-\lambda \left(t-t_0\right)\right),\forall t\ge t_0=0$

则系统(1)在事件触发脉冲控制(2)的作用下达到指数稳定，其中 $\Vert \psi \Vert ={\sup }_{-\tau \le s\le 0}\Vert \psi \left(s\right)\Vert$ 为 $C\left(\left[-\tau ,0\right],R^n\right)$ 上的范数。

3. 主要结果

定理1 针对变时滞系统(1)，若假设1，2成立且存在对称正定矩阵 $P>0$，正数 ${\alpha }_i>0\left(i=1,2,3,\text{4}\right)$， ${\beta }_i>0\left(i=1,2\right)$， ${\beta }_{\text{3}}\ge \text{1}$，使得：

${\aleph }_1=-C^{\text{T}}P-PC+{\alpha }_{1}PA{A}^{\text{T}}P+\frac{u_1^2}{{\alpha }_1}I+{\alpha }_{2}PB{B}^{\text{T}}P+{\alpha }_{4}I+{\beta }_{1}P+2PK\le 0,$ (5)

${\aleph }_{\text{2}}={\left(I-L\right)}^{\text{T}}P\left(I-L\right)-{\beta }_{3}P\le 0,$ (6)

$-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3>0,$ (7)

${\alpha }_{4}I-{\alpha }_{3}PK{K}^{\text{T}}P>0,$ (8)

则在下面的事件触发条件下：

$t_{k+1}=\inf \left\{t\in \left(t_k,\infty \right)|{\Vert e\left(t\right)\Vert }^2\ge {\alpha }_3{x}^{\text{T}}\left(t\right)\left({\alpha }_{\text{4}}I-{\alpha }_{3}PK{K}^{\text{T}}P\right)x\left(t\right)\right\},$ (9)

系统(1)不存在Zeno现象且指数稳定。

证明 首先，我们证明系统(1)不存在Zeno现象。

令 $\Gamma \left(t\right)=e^{\text{T}}\left(t\right)e\left(t\right)$，由于 $e\left(t\right)=x\left(t_k\right)-x\left(t\right)$ 则对 $\Gamma \left(t\right)$ 求导得：

$\begin{array}{c}\stackrel{\dot{}}{\Gamma }\left(t\right)=2e^{\text{T}}\left(t\right)\stackrel{\dot{}}{e}\left(t\right)=-2e^{\text{T}}\left(t\right)\stackrel{\dot{}}{x}\left(t\right)\\ =-2e^{\text{T}}\left(t\right)\left[-Cx\left(t\right)+Af\left(x\left(t\right)\right)+Bg\left(x\left(t-\tau \left(t\right)\right)\right)+Kx\left(t_k\right)\right]\\ \le 4e^{\text{T}}\left(t\right)e\left(t\right)+{\left(-Cx\left(t\right)\right)}^{\text{T}}\left(-Cx\left(t\right)\right)+{\left(Af\left(x\left(t\right)\right)\right)}^{\text{T}}\left(Af\left(x\left(t\right)\right)\right)\\ +{\left(Bg\left(x\left(t-\tau \left(t\right)\right)\right)\right)}^{\text{T}}\left(Bg\left(x\left(t-\tau \left(t\right)\right)\right)\right)+{\left(Kx\left(t_k\right)\right)}^{\text{T}}\left(Kx\left(t_k\right)\right)\end{array}$

$\begin{array}{l}\le 4e^{\text{T}}\left(t\right)e\left(t\right)+\left({\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)x^{\text{T}}\left(t\right)x\left(t\right)+u_2^2{\Vert B\Vert }^2{\left(x\left(t-\tau \left(t\right)\right)\right)}^{\text{T}}\left(x\left(t-\tau \left(t\right)\right)\right)+{\Vert K\Vert }^2{x}^{\text{T}}\left(t_k\right)x\left(t_k\right)\\ \le 2\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)e^{\text{T}}\left(t\right)e\left(t\right)+2\left({\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2+\frac{1}{2}{\Vert K\Vert }^2\right)x^{\text{T}}\left(t_k\right)x\left(t_k\right)+u_2^2{\Vert B\Vert }^2{d}^2\\ \text{=2}\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)\Gamma \left(t\right)\text{+}\tilde{M},\end{array}$

其中 $\tilde{M}=2\left({\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2+\frac{1}{2}{\Vert K\Vert }^2\right)x^{\text{T}}\left(t_k\right)x\left(t_k\right)+u_2^2{\Vert B\Vert }^{\text{2}}{d}^2$。

由于 $e\left(t_k\right)=0$，计算从 $t_k$ 到t的积分可得

$0\le {\Vert e\left(t\right)\Vert }^2\le \frac{\tilde{M}}{2\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)}\left({\text{e}}^{2\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)\left(t-t_k\right)}-1\right),$

由触发条件(9)可知

$\theta \left(x\left(t_{k+1}\right)\right)\le \frac{\tilde{M}}{2\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)}\left({\text{e}}^{2\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)\left(t_{k+1}-t_k\right)}-1\right),$

其中 $\theta \left(x\left(t\right)\right)={\alpha }_3{x}^{\text{T}}\left(t\right)\left({\alpha }_{4}I-{\alpha }_{3}PK{K}^{\text{T}}P\right)x\left(t\right)$。若 $\theta \left(x\left(t_{k+1}\right)\right)=0$ 则 $x\left(t_{k+1}\right)=0$。由于 $f\left(0\right)=g\left(0\right)=0$，显然有 $-C\cdot 0+A\cdot f\left(0\right)+B\cdot g\left(0\right)+K\cdot x\left(t_k\right)=0$，则 $x\left(t_k\right)=0$，这与 $x\left(t_k\right)\ne 0$ 相矛盾，故 $\theta \left(x\left(t_{k+1}\right)\right)>0$。令 $T_k=t_{k+1}-t_k$，因而

$T_k\ge \frac{\ln \left(1+\frac{2\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)\theta \left(x\left(t_{k+1}\right)\right)}{\tilde{M}}\right)}{2\left(2+{\Vert C\Vert }^2+u_1^2{\Vert A\Vert }^2\right)}>0.$

因此， ${\rho }_1=\inf \left\{t_{k+\text{1}}-t_k\right\}=\inf T_k>0$，即系统不存在Zeno现象。

下面证明在控制输入(2)的作用下系统(1)指数稳定。构造Lyapunov函数 $V\left(t\right)=x^{\text{T}}\left(t\right)Px\left(t\right)$，当 $t\ne t_k$ 时，沿着系统(3)的轨线对函数 $V\left(t\right)$ 求导得：

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)=2x^{\text{T}}\left(t\right)P\stackrel{\dot{}}{x}\left(t\right)\\ =2x^{\text{T}}\left(t\right)P\left(-Cx\left(t\right)+Af\left(x\left(t\right)\right)+Bg\left(x\left(t-\tau \left(t\right)\right)\right)+Kx\left(t_k\right)\right)\\ =2x^{\text{T}}\left(t\right)P\left(-Cx\left(t\right)+Af\left(x\left(t\right)\right)+Bg\left(x\left(t-\tau \left(t\right)\right)\right)+Ke\left(t\right)+Kx\left(t\right)\right),\end{array}$

由假设1及引理1得：

$\begin{array}{c}\text{2}{x}^{\text{T}}\left(t\right)PAf\left(x\left(t\right)\right)\le {\alpha }_1{x}^{\text{T}}\left(t\right)PA{A}^{\text{T}}Px\left(t\right)+\frac{1}{{\alpha }_1}{f}^{\text{T}}\left(x\left(t\right)\right)f\left(x\left(t\right)\right)\\ \le {\alpha }_1{x}^{\text{T}}\left(t\right)PA{A}^{\text{T}}Px\left(t\right)+\frac{u_1^2}{{\alpha }_1}{x}^{\text{T}}\left(t\right)x\left(t\right),\end{array}$

$\begin{array}{c}\text{2}{x}^{\text{T}}\left(t\right)PBg\left(x\left(t-\tau \left(t\right)\right)\right)\le {\alpha }_2{x}^{\text{T}}\left(t\right)PB{B}^{\text{T}}Px\left(t\right)+\frac{1}{{\alpha }_2}{g}^{\text{T}}\left(x\left(t-\tau \left(t\right)\right)\right)g\left(x\left(t-\tau \left(t\right)\right)\right)\\ \le {\alpha }_2{x}^{\text{T}}\left(t\right)PB{B}^{\text{T}}Px\left(t\right)+\frac{u_2^2}{{\alpha }_2}{x}^{\text{T}}\left(t-\tau \left(t\right)\right)x\left(t-\tau \left(t\right)\right),\end{array}$

$2x^{\text{T}}\left(t\right)PKe\left(t\right)\le {\alpha }_3{x}^{\text{T}}\left(t\right)PK{K}^{\text{T}}Px\left(t\right)+\frac{1}{{\alpha }_3}{e}^{\text{T}}\left(t\right)e\left(t\right).$

由事件触发条件(9)可知，当 $t\in \left(t_k,t_{k+1}\right)$ 时，

${\Vert e\left(t\right)\Vert }^2<{\alpha }_3{x}^{\text{T}}\left(t\right)\left({\alpha }_{\text{4}}I-{\alpha }_{3}PK{K}^{\text{T}}P\right)x\left(t\right),$

因此， $t\in \left(t_k,t_{k+1}\right)$ 时，

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)<x^{\text{T}}\left(t\right)\left[-PC-C^{\text{T}}P+{\alpha }_{1}PA{A}^{\text{T}}P+\frac{u_1^2}{{\alpha }_1^2}I+{\alpha }_{2}PB{B}^{\text{T}}P+2PK\right]x\left(t\right)\\ +\frac{u_2^2}{{\alpha }_2^2}{x}^{\text{T}}\left(t-\tau \left(t\right)\right)x\left(t-\tau \left(t\right)\right)\\ +{\alpha }_3{x}^{\text{T}}\left(t\right)PK{K}^{\text{T}}Px\left(t\right)+x^{\text{T}}\left(t\right)\left({\alpha }_{4}I-{\alpha }_{3}PK{K}^{\text{T}}P\right)x\left(t\right)\\ =x^T\left(t\right){\aleph }_{1}x\left(t\right)-{\beta }_1{x}^{\text{T}}\left(t\right)Px\left(t\right)+\frac{u_2^2}{{\alpha }_2^2}{x}^{\text{T}}\left(t-\tau \left(t\right)\right)x\left(t-\tau \left(t\right)\right)\\ \le -{\beta }_{1}V\left(t\right)+{\beta }_{2}V\left(t-\tau \left(t\right)\right),\end{array}$

其中 ${\beta }_2=\frac{u_2^2}{{\alpha }_2^2}{\lambda }_{\max }\left(P^{-1}\right)$。

当 $t=t_k$ 时，由 $x\left(t_k^{+}\right)=\left(I-L\right)x\left(t_k\right)$ 及 ${\aleph }_2\le 0$ 可得

$\begin{array}{c}V\left(t_k^{+}\right)=x^{\text{T}}\left(t_k^{+}\right)Px\left(t_k^{+}\right)\\ =x^{\text{T}}\left(t_k\right){\left(I-L\right)}^{\text{T}}P\left(I-L\right)x\left(t_k\right)\\ =x^{\text{T}}\left(t_k\right)\left[{\left(I-L\right)}^{\text{T}}P\left(I-L\right)-{\beta }_{3}P\right]x\left(t_k\right)+x^{\text{T}}\left(t_k\right){\beta }_{3}Px\left(t_k\right)\\ =x^{\text{T}}\left(t_k\right){\aleph }_{2}x\left(t_k\right)+{\beta }_{3}V\left(t_k\right)\\ \le {\beta }_{3}V\left(t_k\right).\end{array}$

对任意 $\epsilon >0$，设 $v\left(t\right)$ 是下列时滞方程的唯一解：

$\{\begin{array}{l}\stackrel{\dot{}}{v}\left(t\right)=-{\beta }_{1}v\left(t\right)+{\beta }_{2}v\left(t-\tau \left(t\right)\right)+\epsilon ,t\ge 0,t\ne t_k\\ v\left(t_k^{+}\right)={\beta }_{3}v\left(t_k\right),t=t_k\\ v\left(t\right)={\lambda }_{\max }\left(P\right){\Vert \psi \left(t\right)\Vert }^2,-\tau \le t\le 0\end{array}$

式中 ${\lambda }_{\max }\left(P\right)$ 为矩阵P的最大特征值。当 $-\tau \le t\le 0$ 时 $V\left(t\right)\le {\lambda }_{\max }\left(P\right){\Vert \psi \left(t\right)\Vert }^2=v\left(t\right)$，由引理2得，当 $t\ge 0$ 时 $v\left(t\right)\ge V\left(t\right)\ge 0$。设 $W\left(t,s\right),t,s\ge 0$ 是线性方程组

$\{\begin{array}{l}\stackrel{\dot{}}{v}\left(t\right)=-{\beta }_{1}v\left(t\right),t\ne t_k\\ v\left(t_k^{+}\right)={\beta }_{3}v\left(t_k\right),t=t_k\end{array}$

的Cauchy矩阵，则

$W\left(t,s\right)={\text{e}}^{-{\beta }_1\left(t-s\right)}\left({\displaystyle {\prod }_{s\le t_k\le t}{\beta }_3}\right).$

因为 ${\beta }_3\ge 1$， ${\rho }_1=\inf \left\{t_{k+1}-t_k\right\}>0$，所以

$W\left(t,s\right)={\text{e}}^{-{\beta }_1\left(t-s\right)}\left({\displaystyle {\prod }_{s\le t_k\le t}{\beta }_3}\right)\le {\text{e}}^{-{\beta }_1\left(t-s\right)}{\beta }_3{}^{\frac{t-s}{{\rho }_1}+1}={\beta }_3{\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)\left(t-s\right)},$ (10)

由参数变分公式得， $t\ge 0$ 时

$\nu \left(t\right)=W\left(t,0\right)\nu \left(0\right)+{\displaystyle {\int }_0^{t}W\left(t,s\right)\times \left[{\beta }_2\nu \left(s-\tau \left(s\right)\right)+\epsilon \right]\text{d}s},$ (11)

因此， $t\ge 0$ 时

$\begin{array}{c}\nu \left(t\right)=W\left(t,0\right)\nu \left(0\right)+{\displaystyle {\int }_0^{t}W\left(t,s\right)\times \left[{\beta }_2\nu \left(s-\tau \left(s\right)\right)+\epsilon \right]\text{d}s}\\ \le {\beta }_3{\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)t}{\lambda }_{\max }\left(P\right){\Vert \psi \left(0\right)\Vert }^2+{\displaystyle {\int }_0^t{\beta }_3{e}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)\left(t-s\right)}\times \left[{\beta }_2\nu \left(s-\tau \left(s\right)\right)+\epsilon \right]\text{d}s}\\ \le \sigma {\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)t}+{\displaystyle {\int }_0^t{\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)\left(t-s\right)}\times \left[{\beta }_2{\beta }_3\nu \left(s-\tau (s)\right)+\epsilon {\beta }_3\right]\text{d}s},\end{array}$ (12)

其中 $\sigma ={\beta }_3{\lambda }_{\max }\left(P\right){\sup }_{-\tau \le t\le 0}\left\{{\Vert \psi \left(t\right)\Vert }^2\right\}$。

定义 $\hslash \left(\rho \right)=2\rho +\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)+{\beta }_2{\beta }_3{\text{e}}^{2\rho \tau }$，则对于连续函数 $\hslash \left(\rho \right)$ 由(7)式可得 $\hslash \left(\text{0}\right)=\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)+{\beta }_2{\beta }_3<0$， $\hslash \left(\infty \right)>0$ 且 $\stackrel{\dot{}}{\hslash }\left(\rho \right)=2+2\tau {\beta }_2{\beta }_3{\text{e}}^{2\rho \tau }>0$，故 $\hslash \left(\rho \right)=0$ 存在唯一解 $\rho >0$。那么当 $-\tau \le t\le 0$， $\rho >0$ 且 ${\beta }_{\text{3}}\ge \text{1}$ 时，

$\begin{array}{l}v\left(t\right)={\lambda }_{\max }\left(P\right){\Vert \psi \left(t\right)\Vert }^2\le {\beta }_3{\lambda }_{\max }\left(P\right){\Vert \psi \left(t\right)\Vert }^2{\text{e}}^{-2\rho t}\\ <\sigma {\text{e}}^{-2\rho t}+\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3},\end{array}$ (13)

下面证明，当 $t>0$ 时

$v\left(t\right)<\sigma {\text{e}}^{-2\rho t}+\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}.$ (14)

若不等式(14)在 $t>0$ 时不成立，则存在 $t^{\text{*}}>0$ 使得

$v\left(t^{\text{*}}\right)\ge \sigma {\text{e}}^{-2\rho t^{*}}+\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3},$ (15)

当 $t<t^{\text{*}}$ 时，

$v\left(t\right)<\sigma {\text{e}}^{-2\rho t}+\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}.$ (16)

由 $\hslash \left(\rho \right)=0$ 及不等式(12)、(16)得：

$\begin{array}{c}v\left(t^{\text{*}}\right)\le \sigma e^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)t^{\text{*}}}+{\displaystyle {\int }_0^t{\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)\left(t^{\text{*}}-s\right)}}\times \left[{\beta }_2{\beta }_{3}v\left(s-\tau \left(s\right)\right)+{\beta }_3\epsilon \right]\text{d}s\\ <{\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)t^{\text{*}}}\left\{\sigma +\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}+{\displaystyle {\int }_0^{t^{*}}{\text{e}}^{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)s}}\times \left[{\beta }_2{\beta }_{3}v\left(s-\tau \left(s\right)\right)+{\beta }_3\epsilon \right]\text{d}s\right\}\\ <{\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)t\text{*}}\{\sigma +\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}+{\displaystyle {\int }_0^{t\text{*}}{\text{e}}^{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)s}}\end{array}$

$\begin{array}{l}\times \left[{\beta }_2{\beta }_3\left(\sigma {\text{e}}^{-2\rho \left(s-\tau \left(s\right)\right)}+\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}\right)+{\beta }_3\epsilon \right]\text{d}s\}\\ <{\text{e}}^{\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)t^{\text{*}}}\{\sigma +\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}+\frac{{\beta }_2{\beta }_3\sigma }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1+2\rho \right)}{\text{e}}^{2\rho \tau }\left[{\text{e}}^{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1+2\rho \right)t^{\text{*}}}-1\right]\\ +\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}\left[{\text{e}}^{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)t^{*}}-1\right]\}\\ =\sigma {\text{e}}^{-2\rho t^{\text{*}}}+\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3},\end{array}$

这与(15)矛盾，故当 $t>0$ 时， $\nu \left(t\right)<\sigma {\text{e}}^{-2\rho t}+\frac{{\beta }_3\epsilon }{-\left(\frac{\ln {\beta }_3}{{\rho }_1}-{\beta }_1\right)-{\beta }_2{\beta }_3}$。因此，当 $\epsilon \to \text{0}$ 时， $\Vert x\left(t\right)\Vert \le \sqrt{{\beta }_3\frac{{\lambda }_{\max }\left(P\right)}{{\lambda }_{\min }\left(P\right)}}\Vert \psi \Vert {\text{e}}^{-\rho t}$，其中 $\rho$ 为 $\hslash \left(\rho \right)=0$ 的解，即系统(1)在事件触发脉冲控制(2)的作用下指数稳定。定理得证。

4. 数值仿真

考虑以下非线性变时滞系统 [11]：

$\stackrel{\dot{}}{x}\left(t\right)=-Cx\left(t\right)+Af\left(x\left(t\right)\right)+Bg\left(x\left(t-\tau \left(t\right)\right)\right)$ (17)

其相应的系数矩阵为： $C=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$， $A=\left[\begin{array}{cc}2& -0.1\\ -5& 3\end{array}\right]$， $B=\left[\begin{array}{cc}-1.5& -0.1\\ -0.2& -2.5\end{array}\right]$，状态向量 $x\left(t\right)={\left(x_1\left(t\right),x_2\left(t\right)\right)}^{\text{T}}$，非线性函数 $f\left(x\left(t\right)\right)={\left(f_1\left(x\left(t\right)\right),f_2\left(x\left(t\right)\right)\right)}^{\text{T}}$， $g\left(x\left(t-\tau \left(t\right)\right)\right)={\left(g_1\left(x\left(t-\tau \left(t\right)\right)\right),g_2\left(x\left(t-\tau \left(t\right)\right)\right)\right)}^{\text{T}}$，且式子中 $f_1(\cdot )=f_{\text{2}}(\cdot )=g_1(\cdot )=g_2(\cdot )=\tanh (\cdot )$，变时滞函数 $\tau \left(t\right)=1+0.3\sin \left(2t\right)\le 1.3=\tau$。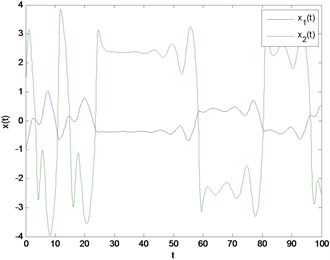图1(a)给出了变时滞系统初值为 ${\left[\begin{array}{cc}-1& 1\end{array}\right]}^{\text{T}}$ 时的相图，图1(b)为其状态轨迹，可以看出在没有控制的情况下状态向量 $x\left(t\right)$ 不稳定。

在事件触发脉冲控制下，参数设置为： ${\alpha }_1={\alpha }_2=1$， ${\alpha }_3=0.182$， ${\alpha }_4=2.322$， $K=\left[\begin{array}{cc}1& 0.99\\ 1& 1\end{array}\right]$， $L=\left[\begin{array}{cc}1.532& -0.732\\ 1.132& -0.232\end{array}\right]$， $P=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$。图2(a)、图3(a)分别为系统(17)在事件触发脉冲控制和脉冲控制下系

统的状态轨迹图，图2(b)、图3(b)分别为两种控制方法下系统的采样时间间隔图。从图2(a)、图3(a)中可以看出，在两种控制方法下系统都可以稳定到原点。由图2(b)、图3(b)可以得到，在本文提出的事件触发脉冲控制下，系统数据采样次数为173，而在脉冲控制下，至少需要的采样次数为500。这说明事件触发脉冲控制方法只需要约34.6%的采样和信息传递次数就能使系统(17)指数稳定。

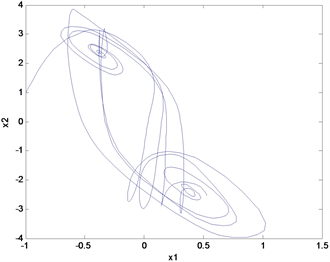(a) (b)

Figure 1. The evolution of the time-varying delay system (17) in the absence of any control. (a) Phase diagram; (b) State trajectories

图1. 无控制时变时滞系统(17)的状态演化。(a) 相图；(b) 状态轨迹

(a) (b)

Figure 2. The evolution of the time-varying delay system (17) under the event-triggered impulsive control. (a) State trajectories; (b) The steps of samplings

图2. 事件触发脉冲控制下变时滞系统(17)的演化过程。(a) 状态轨迹；(b) 采样时间间隔

(a) (b)

Figure 3. The evolution of the time-varying delay system (17) under the impulsive control. (a) State trajectories; (b) The steps of samplings

图3. 脉冲控制下变时滞系统(17)的演化过程。(a) 状态轨迹；(b) 采样时间间隔图

5. 结论

本文为变时滞系统设计了一种事件触发脉冲控制方法，并讨论其稳定性问题。理论计算表明系统在事件触发脉冲控制下不存在Zeno现象。此外，我们通过理论分析得到了变时滞系统在提出的控制方法下指数稳定的充分条件。仿真结果表明本文设计的事件触发脉冲控制方法易于实现，稳定效果好，可以在一定程度上减少数据采样次数，提高资源利用率。今后，我们将进一步研究事件触发脉冲控制在更加复杂的网络环境下的协同问题。