二维Burgers方程的分裂高阶有限差分方法

The Splitting High-Order Finite Difference Method of Two-Dimensional Burgers Equation

摘要: 本文主要研究了二维Burgers方程的分裂高阶差分方法，利用能量的方法，证明了所提出的差分格式在时间上具有二阶收敛率以及在空间上具有四阶收敛率。数值结果验证了算法的精度和有效性。

Abstract: The study is concerned with the splitting higher-order finite difference method of two-dimensional Burgers equation. By using the energy method, the proposed difference scheme is proved to have the second-order convergence rate in time and the fourth-order convergence rate in space. The accuracy and efficiency of the algorithm are verified by numerical findings.

1. 引言

在如今这个科技快速发展的情势下，偏微分方程的理论形成和发展在数学及科学技术中应用广泛，Burgers方程作为其重要分支，应用于数学及社会生活的许多领域，它作为最简单的非线性对流扩散的模型，在湍流、传热、传质、大气、水资源污染及连续随机过程等众多领域中发挥着极其重要的作用。对Burgers方程的深入研究有助于其他非线性问题 [1] 的研究，所以求解非线性Burgers方程的数值解十分有意义。

近年来，关于Burgers方程的数值研究有不少的成果 [2] [3] [4]。文献 [3] 研究了一维Burgers方程的两种线性化差分格式，文献 [1] [3] 研究了二维Burgers方程的Crank-Nicolson格式，并得到了时间二阶和空间二阶的收敛速度。本文参考文献 [5] 中的技巧，采用维数分裂的技巧，提出二维Burgers方程的分裂高阶有限差分方法，并对其稳定性以及收敛性进行理论性分析，最后通过数值算例进行验证。

2. 分裂高阶有限差分方法

考虑如下二维Burgers方程

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+u\frac{\partial u}{\partial y}=V\frac{{\partial }^{2}u}{\partial x^2}+V\frac{{\partial }^{2}u}{\partial y^2}$, (a)

其初边值条件为

$u\left(x,y,0\right)=u\left(x,y\right)$, $\left(x,y\right)\in \Omega$, (b)

$u\left(x,y,t\right)=0$, $\left(x,y\right)\in \partial \text{Ω}$, $t\in \left[0,T\right]$. (c)

其中矩形区域 $\Omega =\left(0,a\right)\times \left(0,b\right)$，时间周期为 $T>0$。

2.1. 记号

为建立差分格式，首先对求解区域

$\Omega =\left\{\left(x,y,t\right)|0\le x\le I,0\le y\le J,0\le t\le T\right\}$ 做网格剖分。取x-和y-方向上的空间步长分别为 $h_x=\frac{a}{I}$， $h_y=\frac{b}{J}$，时间步长为 $\tau =\frac{T}{N}$，其对应网格节点坐标为 $u\left(x_i,y_j,t_n\right)$ 且 $x_i=i\cdot h_x$， $i=0,1,\cdots ,I$ ； $y_j=j\cdot h_y$， $j=0,1,\cdots ,J$ ； $t_n=n\cdot \tau$ ； $n=0,1,\cdots ,N$。记 ${\Omega }_{h_x}=\left\{x_i|0\le x\le I\right\}$， ${\Omega }_{h_y}=\left\{y_j|0\le y\le J\right\}$， ${\Omega }_{{\tau }_n}=\left\{{\tau }_n|0\le \tau \le N\right\}$， ${\Omega }_{h\tau }={\Omega }_{h_x}\times {\Omega }_{h_y}\times {\Omega }_{{\tau }_n}$。

设 $\left\{u_{ij}^n|0\le i\le I,0\le j\le J,0\le n\le N\right\}$ 为一个网格函数。下面，我们定义一些差分算子：

${\delta }_x{u}_{ij}^n=\frac{u_{i+1,j}^n-u_{ij}^n}{h_x}$, $u_{ij}^n=\frac{u_{i,j+1}^n-u_{ij}^n}{h_y}$,

${\delta }_t{u}_{ij}^n=\frac{u_{ij}^{n+1}-u_{ij}^n}{\tau }$,

${\delta }_{\hat{x}}{u}_{ij}^n=\frac{u_{i+1,j}^n-u_{i-1,j}^n}{2h_x}$, ${\delta }_{\hat{y}}{u}_{ij}^n=\frac{u_{i,j+1}^n-u_{i,j-1}^n}{2h_y}$,

${\delta }_x^2{u}_{ij}^n=\frac{u_{i+1,j}^n-2u_{ij}^n+u_{i-1,j}^n}{h_x^2}$, ${\delta }_y^2{u}_{ij}^n=\frac{u_{i,j+1}^n-2u_{ij}^n+u_{i,j-1}^n}{h_y^2}$.

根据泰勒展开式所得 为二阶，为提升至四阶，引入高阶紧算子，

$L_x{u}_{ij}^n=\frac{1}{12}\left(u_{i+1,j}^n+10u_{ij}^n+u_{i-1,j}^n\right)$,

$L_y{u}_{ij}^n=\frac{1}{12}\left(u_{i,j+1}^n+10u_{ij}^n+u_{i,j-1}^n\right)$,

$M_x{u}_{ij}^n=\frac{1}{6}\left(u_{i+1,j}^n+4u_{ij}^n+u_{i-1,j}^n\right)$,

$M_y{u}_{ij}^n=\frac{1}{6}\left(u_{i,j+1}^n+4u_{ij}^n+u_{i,j-1}^n\right)$,

满足

$L_x\frac{{\partial }^2{u}_{ij}^n}{\partial x^2}={\delta }_x^2{u}_{ij}^n+o\left(h_x^4\right)$,

$L_y\frac{{\partial }^2{u}_{ij}^n}{\partial x^2}={\delta }_y^2{u}_{ij}^n+o\left(h_y^4\right)$,

$M_x\frac{\partial u_{ij}^n}{\partial x}={\delta }_{\hat{x}}{u}_{ij}^n+o\left(h_x^4\right)$,

$M_y\frac{\partial u_{ij}^n}{\partial x}={\delta }_{\hat{y}}{u}_{ij}^n+o\left(h_y^4\right)$.

2.2. 差分格式的建立

根据抛物方程的分裂技巧，在时间步 $\left(t_n,t_{n+1}\right]$ 下，将方程(a)分裂成两个方程

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=V\frac{{\partial }^{2}u}{\partial x^2}$, (2.2.1)

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial y}=V\frac{{\partial }^{2}u}{\partial y^2}$. (2.2.2)

令 $U_{ij}^n$ 是 $u_{ij}^n$ 的近似解，对于方程(2.2.1)~(2.2.2)，我们提出分裂差分格式：

$\frac{U_{ij}^{n+\frac{1}{2}}-U_{ij}^n}{\tau }+\frac{1}{3}\varphi \left(U_{ij}^{n+\frac{1}{4}}\right)=V{L}_x^{-1}{\delta }_x^2{U}_{ij}^{n+\frac{1}{4}}$, (2.2.3)

$\frac{U_{ij}^{n+1}-U_{ij}^{n+\frac{1}{2}}}{\tau }+\frac{1}{3}\psi \left(U_{ij}^{n+\frac{3}{4}}\right)=V{L}_y^{-1}{\delta }_y^2{U}_{ij}^{n+\frac{3}{4}}$. (2.2.4)

其中

$\varphi \left(U_{ij}^{n+\frac{1}{4}}\right)=U_{ij}^{n+\frac{1}{4}}{M}_x^{-1}{\delta }_{\hat{x}}{U}_{ij}^{n+\frac{1}{4}}+M_x^{-1}{\delta }_{\hat{x}}{\left(U_{ij}^{n+\frac{1}{4}}\right)}^2$，

$\psi \left(U_{ij}^{n+\frac{3}{4}}\right)=U_{ij}^{n+\frac{3}{4}}{M}_y^{-1}{\delta }_{\hat{y}}{U}_{ij}^{n+\frac{3}{4}}+M_y^{-1}{\delta }_{\hat{y}}{\left(U_{ij}^{n+\frac{3}{4}}\right)}^2$.

格式的边界条件为

$U\left(x,y,t\right)=0$, $\left(x,y\right)\in \partial \Omega$, $t\in \left[0,T\right]$, (2.2.5)

初值条件为

$U_{ij}^0=u\left(x,y\right)$. (2.2.6)

2.3. 守恒性和收敛性分析

为了方便稳定性和收敛性的证明，我们给出一些内积和范数的定义。令 $V_h=\left\{u_{ij}|\left(x_i,y_j\right)\in {\bar{\Omega }}_h,u_{ij}|\partial {\Omega }_h=0\right\}$，我们定义离散的内积和范数

$\left(u,v\right)={\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{u}_{ij}{v}_{ij}{h}_x{h}_y}}$,

${\left(u,v\right)}_x={\displaystyle \underset{i=0}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{u}_{ij}{v}_{ij}{h}_x{h}_y}}$,

${\left(u,v\right)}_y={\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=0}{\overset{J-1}{\sum }}{u}_{ij}{v}_{ij}{h}_x{h}_y}}$,

$\Vert u\Vert =\sqrt{\left(u,u\right)}$, ${\Vert u\Vert }_x=\sqrt{{\left(u,u\right)}_x}$, ${\Vert u\Vert }_y=\sqrt{{\left(u,u\right)}_y}$.

为了证明紧格式的离散电荷和能量的守恒性，我们给出以下一些引理。

引理2.3.1 [5] 对于网格函数 $u,\nu \in V_h$，我们有

$\left({\delta }_x^{2}u,\nu \right)=-{\left({\delta }_{x}u,{\delta }_x\nu \right)}_x$, $\left({\delta }_y^{2}u,\nu \right)=-{\left({\delta }_{y}u,{\delta }_y\nu \right)}_y$.

引理2.3.2 [5] 对于网格函数 $\mu ,\nu \in V_h$，我们有

$\left(L_{x}u,\nu \right)=\left(u,L_x\nu \right)$, $\left(M_{x}u,\nu \right)=\left(u,M_x\nu \right)$,

$\left(L_x^{-1}u,\nu \right)=\left(u,L_x^{-1}\nu \right)$, $\left(M_x^{-1}u,\nu \right)=\left(u,M_x^{-1}\nu \right)$.

引理2.3.3 [5] 对于网格函数 $U,V\in V_h$，若 ${\Vert U\Vert }_{L_2}$ 和 ${\Vert V\Vert }_{L_2}$ 有界，则存在正常数C，使得

$\left(\varphi \left(U\right)-\varphi \left(V\right),U-V\right)\le C\left({\Vert U-V\Vert }^2+{\Vert {\delta }_x\left(U-V\right)\Vert }_x^2\right)$.

引理2.3.4对于对称的正定矩阵 ${\mathcal{L}}_x^{-1}$， ${\mathcal{M}}_x^{-1}$，我们有

${\mathcal{L}}_x^{-1}={\mathcal{R}}_1^{\text{T}}{\mathcal{R}}_1$, ${\mathcal{M}}_x^{-1}={\mathcal{R}}_2^{\text{T}}{\mathcal{R}}_2$.

和

$C_0\Vert U^n\Vert \le \Vert {\mathcal{R}}_1{U}^n\Vert \le C_1\Vert U^n\Vert$, $C_3\Vert U^n\Vert \le \Vert {\mathcal{R}}_2{U}^n\Vert \le C_4\Vert U^n\Vert$

其中 ${\mathcal{R}}_1=Chol\left({\mathcal{L}}_x^{-1}\right)$， ${\mathcal{R}}_2=Chol\left({\mathcal{M}}_x^{-1}\right)$， $C_i\left(i=1,2,3,4\right)$ 为正常数。

证：因为 ${\mathcal{L}}_x^{-1}$ 是一个对称的正定矩阵，故存在矩阵 ${\mathcal{R}}_1$，其中 ${\mathcal{R}}_1$ 为上三角矩阵，满足 ${\mathcal{L}}_x^{-1}={\mathcal{R}}_1^{\text{T}}{\mathcal{R}}_1$，其中 ${\mathcal{R}}_1=Chol\left({\mathcal{L}}_x^{-1}\right)$。

根据矩阵中范数的定义，我们有

$C_0\Vert U^n\Vert \le \Vert {\mathcal{R}}_1{U}^n\Vert \le C_1\Vert U^n\Vert$

同样，矩阵 ${\mathcal{M}}_x^{-1}$， ${\mathcal{R}}_2$ 也有类似的结果。

引理2.3.5 [5] 对于网格函数 $u\in V_h$，我们有

${\Vert {\delta }_x{u}^n\Vert }_x^2\le \frac{4}{h_x^2}{\Vert u^n\Vert }^2$, ${\Vert {\delta }_y{u}^n\Vert }_y^2\le \frac{4}{h_y^2}{\Vert u^n\Vert }^2$.

引理2.3.6 [5] (Gronwall不等式)设 $w^n\ge 0$ 且存在常数 $C_3,C_4$，使得 $w^n\le C_3+C_4\tau {\displaystyle {\sum }_{k=0}^{n-1}{w}^k}$， $0<n\tau <T$，

那么

$w^n\le C_3{\text{e}}^{C_{4}T}$, $0<n\tau <T$.

定理2.3.1 (守恒性)分裂高阶有限差分格式(2.2.3)~(2.2.6)满足离散的电荷守恒，即

$Q^{n+1}=Q^n$. (2.3.1)

其中

$Q^n={\displaystyle {\sum }_{i=1}^{I-1}{\displaystyle {\sum }_{j-1}^{J-1}{U}_{ij}^n{h}_x{h}_y}}$. (2.3.2)

对任意的 $n\ge 0$ 成立。

证：对方程(2.2.3)两端同时乘以 $h_x{h}_y$，i从1到 $I-1$ 求和，j从1到 $J-1$ 求和：

$h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\frac{U_{ij}^{n+\frac{1}{2}}-U_{ij}^n}{\tau }}}+\frac{1}{3}{h}_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\varphi \left(U_{ij}^{n+\frac{1}{4}}\right)}}-V{h}_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{L}_x^{-1}{\delta }_x^2{U}_{ij}^{n+\frac{1}{4}}}}=0$

考虑边界条件(2.2.5)，有

$U_{0j}^n=U_{1j}^n=U_{i0}^n=U_{i1}^n=U_{I-1,j}^n=U_{Ij}^n=U_{i,J-1}^n=U_{iJ}^n=0$

$\begin{array}{c}{h}_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{L}_x^{-1}{\delta }_x^2{U}_{ij}^{n+\frac{1}{4}}}}=h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{\delta }_x^2{U}_{ij}^{n+\frac{1}{4}}}}=h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\frac{U_{i+1,j}^{n+\frac{1}{4}}-2U_{ij}^{n+\frac{1}{4}}+U_{i-1,j}^{n+\frac{1}{4}}}{h{x}^2}}}\\ =h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\left[\left(U_{i+1,j}^{n+\frac{1}{4}}-U_{ij}^{n+\frac{1}{4}}\right)-\left(U_{ij}^{n+\frac{1}{4}}-U_{i-1,j}^{n+\frac{1}{4}}\right)\right]}}=0\end{array}$

因为

$\begin{array}{l}{h}_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\varphi \left(U_{ij}^{n+\frac{1}{4}}\right)}}\\ =h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\left(U_{ij}^{n+\frac{1}{4}}{M}_x^{-1}{\delta }_{\hat{x}}{U}_{ij}^{n+\frac{1}{4}}+M_x^{-1}{\delta }_{\hat{x}}{\left(U_{ij}^{n+\frac{1}{4}}\right)}^2\right)}}\\ =h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\left(M_x^{-1}{U}_{ij}^{n+\frac{1}{4}}{\delta }_{\hat{x}}{U}_{ij}^{n+\frac{1}{4}}\right)}}+h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{\delta }_{\hat{x}}{\left(U_{ij}^{n+\frac{1}{4}}\right)}^2}}\\ =h_x{h}_y\left({\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{U}_{i+1,j}^{n+\frac{1}{4}}}}\right)\left({\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{\delta }_{\hat{x}}{U}_{ij}^{n+\frac{1}{4}}}}\right)+h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{\delta }_{\hat{x}}{\left(U_{ij}^{n+\frac{1}{4}}\right)}^2}}=0\end{array}$

所以

$h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}\frac{U_{ij}^{n+\frac{1}{2}}-U_{ij}^n}{\tau }}}=0$

即

$h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{U}_{ij}^{n+\frac{1}{2}}}}=h_x{h}_y{\displaystyle \underset{i=1}{\overset{I-1}{\sum }}{\displaystyle \underset{j=1}{\overset{J-1}{\sum }}{U}_{ij}^n}}$

即 $Q^{n+1}=Q^n$，因此(2.2.3)~(2.2.6)满足电荷守恒。

推论 (稳定性)差分格式(2.2.3)~(2.2.6)是无条件稳定的。

证：由定理2.3.1可得：对于任意的 $n\ge 0$，有

$\Vert U^{n+1}\Vert =\Vert U^n\Vert =\Vert U^{n-1}\Vert =\cdots =\Vert U^1\Vert =\Vert U^0\Vert$ 成立

因此，差分格式(2.2.3)~(2.2.6)是无条件稳定的。

定理2.3.2 (收敛性）假设问题(a)~(c)的精确解ν足够光滑，令u是分裂高阶有限差分格式(2.2.3)~(2.2.6)的数值解，对于固定的 $T>0$，存在一个独立的 $\tau$， $h_x$， $h_y$ 和正常数C，满足：

$\underset{1\le n\le N}{\max }\Vert {\nu }^n-u^n\Vert \le C\left({\tau }^2+h_x^4+h_y^4\right)$.

证：令截断误差

${\xi }_{ij}^n=\frac{{\nu }_{ij}^{n+\frac{1}{2}}-{\nu }_{ij}^n}{\tau }+\frac{1}{3}\varphi \left({\nu }_{ij}^{n+\frac{1}{4}}\right)-V{L}_x^{-1}{\delta }_x^2{\nu }_{ij}^{n+\frac{1}{4}}$,

${\eta }_{ij}^n=\frac{{\nu }_{ij}^{n+1}-{\nu }_{ij}^{n+\frac{1}{2}}}{\tau }+\frac{1}{3}\psi \left({\nu }_{ij}^{n+\frac{3}{4}}\right)-V{L}_y^{-1}{\delta }_y^2{\nu }_{ij}^{n+\frac{3}{4}}$.

由(2.2.3)易得：令 $e_{ij}^n={\nu }_{ij}^n-u_{ij}^n$

有：

${\xi }_{ij}^n=\frac{e_{ij}^{n+\frac{1}{2}}-e_{ij}^n}{\tau }+\frac{1}{3}\varphi \left({\nu }_{ij}^{n+\frac{1}{4}}\right)-\frac{1}{3}\varphi \left(u_{ij}^{n+\frac{1}{4}}\right)-V{L}_x^{-1}{\delta }_x^2{e}_{ij}^{n+\frac{1}{4}}$.

让 ${\xi }_{ij}^n$ 与 $e_{ij}^{n+\frac{1}{2}}+e_{ij}^n$ 作内积：

$\begin{array}{c}\left({\xi }^n,e^{n+\frac{1}{2}}+e^n\right)=\frac{1}{\tau }\left({\Vert e^{n+\frac{1}{2}}\Vert }^2-{\Vert e^n\Vert }^2\right)+\frac{1}{3}\left(\varphi \left({\nu }_{ij}^{n+\frac{1}{4}}\right)-\frac{1}{3}\varphi \left(u_{ij}^{n+\frac{1}{4}}\right),e^{n+\frac{1}{2}}+e^n\right)\\ -V\left(L_x^{-1}{\delta }_x^2{e}^{n+\frac{1}{4}},e^{n+\frac{1}{2}}+e^n\right)\end{array}$.

由引理2.3.3：

$\varphi \left({\nu }_{ij}^{n+\frac{1}{4}}\right)-\varphi \left(u_{ij}^{n+\frac{1}{4}}\right)\le C\left({\Vert e^{n+\frac{1}{2}}\Vert }^2+{\Vert e^n\Vert }^2+{\Vert {\delta }_x{e}^{n+\frac{1}{2}}\Vert }_x^2+{\Vert {\delta }_x{e}^n\Vert }_x^2\right)$. (2.3.3)

根据引理2.3.4：

$\begin{array}{l}\left|L_x^{-1}{\delta }_x^2{e}^{n+\frac{1}{4}},e^{n+\frac{1}{2}}+e^n\right|\\ =\left|R_1{\delta }_x^2{e}^{n+\frac{1}{4}},R_1\left(e^{n+\frac{1}{2}}+e^n\right)\right|=\left|-\left[R_1{\delta }_x{e}^{n+\frac{1}{4}},R_1{\delta }_x{\left(e^{n+\frac{1}{2}}+e^n\right)}_x\right]\right|\\ =\frac{1}{2}{\Vert R_1{\delta }_x\left(e^{n+\frac{1}{2}}+e^n\right)\Vert }_x^2\le \frac{1}{2}{\Vert {\delta }_x\left(e^{n+\frac{1}{2}}+e^n\right)\Vert }_x^2\le {\Vert {\delta }_x{e}^{n+\frac{1}{2}}\Vert }_x^2+{\Vert {\delta }_x{e}^n\Vert }_x^2\end{array}$, (2.3.4)

又：

$\left({\xi }^n,e^{n+\frac{1}{2}}+e^n\right)\le {\Vert {\xi }^n\Vert }^2+2{\Vert e^{n+\frac{1}{2}}\Vert }^2+2{\Vert e^n\Vert }^2$, (2.3.5)

将(2.3.3)~(2.3.5)代入，则有：

$\begin{array}{c}\frac{1}{\tau }\left({\Vert e^{n+\frac{1}{2}}\Vert }^2-{\Vert e^n\Vert }^2\right)\le {\Vert {\xi }^n\Vert }^2+2{\Vert e^{n+\frac{1}{2}}\Vert }^2+2{\Vert e^n\Vert }^2+C{\Vert e^{n+\frac{1}{2}}\Vert }^2+C{\Vert e^n\Vert }^2\\ +C{\Vert {\delta }_x{e}^{n+\frac{1}{2}}\Vert }_x^2+C{\Vert {\delta }_x{e}^n\Vert }_x^2+V{\Vert {\delta }_x{e}^{n+\frac{1}{2}}\Vert }_x^2+V{\Vert {\delta }_x{e}^n\Vert }_x^2\end{array}$,

所以：

$\begin{array}{c}{\Vert e^{n+\frac{1}{2}}\Vert }^2-{\Vert e^n\Vert }^2\le \tau {\Vert {\xi }^n\Vert }^2+\tau \left(2+C\right){\Vert e^{n+\frac{1}{2}}\Vert }^2+\tau \left(2+C\right){\Vert e^n\Vert }^2\\ +\tau \left(V+C\right){\Vert {\delta }_x{e}^{n+\frac{1}{2}}\Vert }_x^2+\tau \left(V+C\right){\Vert {\delta }_x{e}^n\Vert }_x^2\end{array}$,

由引理2.3.5得：

${\Vert e^{n+\frac{1}{2}}\Vert }^2-\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right){\Vert e^{n+\frac{1}{2}}\Vert }^2\le {\Vert e^n\Vert }^2+\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right){\Vert e^n\Vert }^2+\tau {\Vert {\xi }^n\Vert }^2$,

即：

$\left[1-\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right)\right]{\Vert e^{n+\frac{1}{2}}\Vert }^2\le \left[1+\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right)\right]{\Vert e^n\Vert }^2+\tau {\Vert {\xi }^n\Vert }^2$

我们假设 $\tau =o\left(h_x^2\right)$，有 $1-\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right)>0$

则：

${\Vert e^{n+\frac{1}{2}}\Vert }^2\le \frac{1+\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right)}{1-\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right)}{\Vert e^n\Vert }^2+\frac{\tau }{1-\tau \left(2+C+\frac{4}{h_x^2}\left(V+C\right)\right)}{\Vert {\xi }^n\Vert }^2$

令 $P_1=2+C+\frac{4}{h_x^2}\left(V+C\right)$，则有：

${\Vert e^{n+\frac{1}{2}}\Vert }^2\le \frac{1+\tau P_1}{1-\tau P_1}{\Vert e^n\Vert }^2+\frac{\tau }{1-\tau P_1}{\Vert {\xi }^n\Vert }^2$ (2.3.6)

类似地：由方程(2.2.4)，令 $P_2=2+C+\frac{4}{h_y^2}\left(V+C\right)$，有：

${\Vert e^{n+1}\Vert }^2\le \frac{1+\tau P_2}{1-\tau P_2}{\Vert e^{n+\frac{1}{2}}\Vert }^2+\frac{\tau }{1-\tau P_2}{\Vert {\eta }^n\Vert }^2$ (2.3.7)

由(2.3.6)，(2.3.7)得到：

${\Vert e^{n+1}\Vert }^2\le \frac{\left(1+P_1\tau \right)\left(1+P_2\tau \right)}{\left(1-P_1\tau \right)\left(1-P_2\tau \right)}{\Vert e^n\Vert }^2+\frac{\tau }{1-P_2\tau }{\Vert {\eta }^n\Vert }^2+\frac{\tau }{1-P_1\tau }\cdot \frac{1+P_2\tau }{1-P_2\tau }{\Vert {\xi }^n\Vert }^2$

即

$\begin{array}{c}{\Vert e^{n+1}\Vert }^2\le \left(1+C_1\tau \right){\Vert e^n\Vert }^2+C_2\tau \left({\Vert {\xi }^n\Vert }^2+{\Vert {\eta }^n\Vert }^2\right)\\ \le \left(1+C_1\tau \right){\Vert e^n\Vert }^2+C_2\tau {\left({\tau }^2+h_x^4+h_y^4\right)}^2\end{array}$

又 $e^0=0$，由Gronwall不等式：

$\underset{1\le n\le N}{\max }\Vert {\nu }^n-u^n\Vert \le C\left({\tau }^2+h_x^4+h_y^4\right)$.

3. 数值算例

通过算例验证数值结果，考虑二维Burgers方程

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+u\frac{\partial u}{\partial y}=V\frac{{\partial }^{2}u}{\partial x^2}+V\frac{{\partial }^{2}u}{\partial y^2}$

区域为 $\left[0,1\right]\times \left[0,1\right]$，精确解为

$u\left(x,y,t\right)=\exp \left(-2{\pi }^{2}t\right)\sin \left(\pi x\right)\cos (\; \pi \; y\; )$

初始条件和边界条件有精确解直接得到。

表1和表2列出了分裂高阶有限差分格式具有空间四阶的收敛率、时间二阶的收敛率，这个结果和我们的理论分析是一致的。

Table 1. When $t={10}^{-6}$ , space step error and convergence order, where $\tau ={10}^{-7}$， $h_x=h_y=h$

表1. 当 $t={10}^{-6}$ 时，空间步长的误差和收敛阶，其中 $\tau ={10}^{-7}$， $h_x=h_y=h$

Table 2. When $t=0.1$, space step error and convergence order, where $h_x=h_y=0.1$

表2. 当 $t=0.1$ 时，时间步长的误差和收敛阶，其中 $h_x=h_y=0.1$

我们考虑下方的精确解

$u\left(x,y,t\right)=\exp \left(-k{\pi }^{2}t\right)\sin \left(\pi x\right)\cos (\; \pi \; y\; )$

表3可以看出，当k的值发生变化时，时间步长和空间步长分别为 $h_x=h_y=0.2$， $\tau ={10}^{-7}$，我们提出的差分格式的电荷的误差足够小，并且始终为正值，因此差分格式满足电荷守恒，也验证了定理2.3.1的分析结果。

Table 3. When $h_x=h_y=0.2$， $\tau ={10}^{-7}$, space error and convergence order of different exact solutions

表3. 当 $h_x=h_y=0.2$， $\tau ={10}^{-7}$ 时，不同精确解的时间步长的误差和收敛阶

图1和图2分别展示了 $\tau ={10}^{-7},h_x=h_y=0.05$ 时，差分格式的数值解和精确解的图像。可以看出，精确解和数值解的三维立体图是完全一致的，而且曲面的几何特性也是完全相同的。而且我们发现，当空间步长 $h_x,h_y$ 越小时，网格剖分越密集，Burgers方程的解模拟的更加精密。

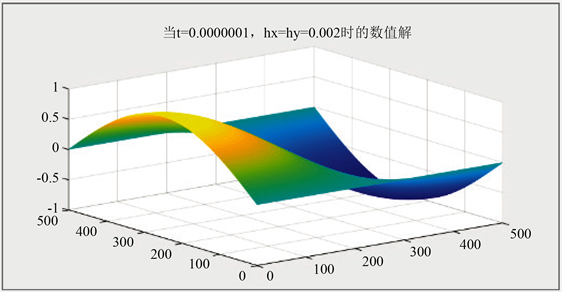
Figure 1. When $\tau ={10}^{-7}$, $h_x=h_y=0.002$, numerical solutions of difference schemes

图1. $\tau ={10}^{-7}$， $h_x=h_y=0.002$ 时，差分格式的数值解

Figure 2. When $\tau ={10}^{-7}$, $h_x=h_y=0.002$, the exact solutions of difference schemes

图2. $\tau ={10}^{-7}$， $h_x=h_y=0.002$ 时，差分格式的精确解

4. 结论

通过抛物型方程的高精度分裂方法 [6] [7]，我们提出了二维Burgers方程的高阶分裂有限差分方法。借用能量法，我们证明了所提格式是守恒的，并且满足时间二阶、空间四阶的收敛性。最后，数值算例和理论结果一致。

基金项目

大学生创新创业训练计划项目(项目编号202010059074)。