石墨烯内聚能的密度泛函理论研究

DFT Studies on the Cohesive Energy of Graphene

摘要: 本文基于第一性原理和密度泛函理论，在局域密度近似以及广义梯度近似下，研究了石墨烯的几何结构和内聚能。石墨烯是由碳原子组成的六角形结构，通过密度泛函理论的计算程序，计算得到了石墨烯体系的总能量，以及孤立碳原子体系的总能量。计算结果表明：石墨烯的内聚能约为−9~−10 eV，对于不同的计算方法及参数，得到的内聚能总为负，这表明石墨烯结构相对于孤立的碳原子来说能量更低。因此相比于孤立的碳原子来说，吸引的相互作用使得系统更倾向于形成石墨烯的结构，说明石墨烯的结构是稳定的。通过本计算模拟研究可对今后石墨烯的结构以及新型结构(例如转角石墨烯)的性能研究及应用发展提供理论参考。

Abstract: In this paper, the geometric structure and cohesive energy of graphene are investigated under local density approximation (LDA) as well as generalized gradient approximation (GGA) based on first principles and density functional theory. Graphene is a hexagonal structure composed of carbon atoms. The total energy of the graphene system and the total energy of the isolated carbon atom system are calculated by the density functional theory. The calculation results show that the cohesive energy of graphene is about -9 to -10eV, and for different calculation methods and parameters, the cohesive energy obtained is always negative, which indicates that the graphene structure has lower energy relative to the isolated carbon atoms. Therefore, the attractive interaction makes the system more inclined to form the graphene structure compared to the isolated carbon atoms, indicating that the graphene structure is stable. This computational simulation study can provide a theoretical reference for the future development of graphene structures, as well as the performance studies and applications of novel structures (e.g., twist graphene).

1. 引言

2004年，英国学者Geim和Novoselov [1] 发现他们可以用一种很简易的方式获得愈来愈薄的石墨薄片。他们通过从高定向热解石墨中剥离出石墨片，然后将薄片的两面粘在胶带上面，进一步撕开胶带从而将石墨一分为二。正是通过不断地这样操作，最终可以得到仅由一层碳原子构成的石墨烯结构。石墨烯是一种由碳原子组成六角型呈蜂巢晶格的二维材料 [2]，由于其具有优良的光学、力学、电学性能以及丰富的物理特性，在物理、材料学、加工、能源、医学等领域有着广阔的应用前景 [3] [4] [5]，近些年来一直是人们研究的热点。

2. 计算方法及过程

2.1. 理论方法

基于密度泛函理论 [6]，可以求的体系的总能量。对于本文采用的计算方法来说，离子势采用了赝势，电子波函数通过平面波基组来展开，计算可以给出体系的基态能量以及电子态密度，从而允许计算和总能量相关的任意物理量，如：晶格常数、弹性常数、几何结构、能带结构等。

考虑Born-Oppenheimer近似 [7]，可以将核与电子部分变量分离。对于固定的核坐标，最终的总能量只需将当前核坐标下的电子部分能量加上核的势能即可(核的动能一般可以不作考虑)。对于电子部分来说，基于密度泛函理论，将计算的电子部分的总能量写成密度的泛函，分为四个部分，具体表达式为 [8]：

$E\left[\rho \right]=T_0\left[\rho \right]+U_{ext}\left[\rho \right]+E_{cl}\left[\rho \right]+E_{xc}\left[\rho \right]$ (1)

其中， $\rho$ 是电子密度， $T_0\left[\rho \right]$ 是非相互作用电子动能项， $U_{ext}\left[\rho \right]$ 是外势项， $E_{cl}\left[\rho \right]$ 是库伦相互作用项， $E_{xc}\left[\rho \right]$ 是交换关联项。对于电荷密度 $\rho$ 来说，它的值可以通过体系波函数来得到，具体的表达式为：

$\rho \left(r\right)={\displaystyle {\sum }_{i=1}^N{\left|{\varphi }_i^{KS}\left(r\right)\right|}^2}$ (2)

根据Hohenberg-Kohn定理 [7]，在粒子数不变的约束条件下，对能量泛函取极小值可以得到体系的基态波函数，于是通过对波函数求变分，即可导出Kohn-Sham方程 [9]，这是一个非相互作用电子的薛定谔方程：

$\left[-\frac{1}{2}{\nabla }_i^2+{\hat{V}}_{eff}\left(r\right)\right]{\varphi }_i^{KS}\left(r\right)={ϵ}_i{\varphi }_i^{KS}\left(r\right)$ (3)

其中， ${\hat{V}}_{eff}\left(r\right)$ 是非局域的有效势，它包含了电子–核的相互作用(外势项)，电子–电子的相互作用(库伦项)，以及交换关联项。更进一步地，电子部分总能量的泛函在Kohn-Sham的框架下可以写为：

$E\left[\rho \right]={\displaystyle {\sum }_{i=1}^N{ϵ}_i}-\frac{1}{2}{\displaystyle \iint \frac{\rho \left(r\right)\rho \left(r^{\prime }\right)}{\left|r-r^{\prime }\right|}\text{d}r\text{d}{r}^{\prime }}-{\displaystyle \int {\hat{V}}_{xc}\left(r\right)\rho \left(r\right)\text{d}r}+E_{xc}\left[\rho \right]$ (4)

其中，右边的第一项为轨道能量之和，第二项为库伦项，第三项为交换关联势，最后一项为交换关联关

于密度的泛函。对于最后一项 $E_{xc}\left[\rho \right]$ 来说，需要做近似，常见的近似方法有局域密度近似LDA [10] 以及

广义梯度近似GGA [11] 等。

对于电子–核之间的相互作用(外势)，使用了赝势 [12] [13]。赝势是针对原子设计的或构造的，是替换原子的全电子势的一种近似势，这种近似势把内壳层的电子隐去了，只考虑价电子。赝势的构造需要满足四个基本条件：1) 赝波函数没有径向节点；2) 在截断半径之外，对给定角动量量子数的价电子径向赝波函数要与全电子情况下的价电子径向波函数相同；3) 在截断半径内，赝波函数和真实波函数的总电荷数一致；4) 对给定角动量量子数的价电子径向赝波函数要与全电子情况下的价电子径向波函数，要给出相同的价电子本征值。通过赝势的构造，可以减少基底的数目，从而减少计算量。赝势的构造方法有很多，例如模守恒赝势(Norm-conserving) [14] 以及超软赝势(Ultra-soft) [15]。

另一方面，可将之前的Kohn-Sham方程和总能量表达式转换到动量空间，即可得到动量空间下的Kohn-Sham方程和总能量表达分别为：

${\displaystyle {\sum }_{G^{\prime }}\left[\frac{1}{2}{\left|k+G^{\prime }\right|}^2{\delta }_{G{G}^{\prime }}+V_{kG{G}^{\prime }}^{eff}\right]{\varphi }_j\left(G^{\prime }\right)}={ϵ}_j{\varphi }_j\left(G\right)$ (5)

$\begin{array}{c}{E}_{tot}={\displaystyle \underset{j}{\sum }{ϵ}_j}-\Omega \frac{1}{2}{\displaystyle \underset{G\ne 0}{\sum }{V}_{coul}\left(G\right){\rho }^{*}\left(G\right)}-\Omega {\displaystyle \underset{G\ne 0}{\sum }\left[V_{xc}\left(G\right)-{ϵ}_{xc}\left(G\right)\right]{\rho }^{*}\left(G\right)}\\ +{\displaystyle {\sum }_{\nu }{\alpha }_{\nu }}{\displaystyle {\sum }_{\mu }{Z}_{\mu }}+{\gamma }_{Ewald}\end{array}$ (6)

其中，总能量的表达式加上了核–核相互作用的贡献。

本次计算采用的是平面波基组展开，理论上说这种展开形式所包含的平面波数量是无限多的，因此需要做动能截断，即包含的平面波动能小于某个设定的截止能量，具体的表达式如下：

$\frac{{\hslash }^2}{2m}{\left|k+G\right|}^2\le E_{cutoff}$ (7)

由于动能的截断，会使得平面波基组不完备，从而使计算产生误差，但是随着截止能量的增大，误差是减小的，因此总可以通过加大截断能量来减少计算的误差。

对于平面波方法来说，总是需要周期性的边界条件。对于本次计算中涉及到的孤立原子，可以将其放到盒子的中心，使得盒子之间的波函数没有交叠；对于二维的石墨烯结构，可以将其垂直与表面方向的晶格常数取大一些，使得层与层之间的波函数尽可能没有交叠，从而构造出三维的周期性边界条件。因此，对于构造出的三维周期性结构，我们可以使用周期性边界条件。

另一方面，对于第一布里渊区内的K点积分，需要将积分离散化，从而对k空间一个小区域，可以选取一个代表的k点波函数来计算电子密度。

在实际的计算过程中，需要自洽计算，大致方法是通过给定初始的平面波函数的展开系数，进一步由波函数构造体系的电荷密度，接着在给定的赝势及交换关联近似下，、计算矩阵元并求解Kohn-Sham方程，从而得到一组新的平面波展开系数及新的电荷密度，将新产生的和之前的对比，当差值满足收敛条件时，计算终止，否则重复之前的步骤。于是，基于密度泛函理论，在Kohn-Sham方程的框架下我们可以求解体系的总能。

2.2. 计算石墨烯的几何结构

对于石墨烯体系，为了突出其二维结构的特性，在构建晶胞的时候，将垂直于表面方向的晶格常数取得相对较大，从而突出层状的结构。通过几何结构优化，最终构建的结构示意图如图1所示。类似地，对于孤立的碳原子来说，将其放入一个较大的晶胞盒子里，从而使原子的波函数之间没有交叠，同时满足周期性的边界条件，最终构建的几何结构如图2所示。

Figure 1. Schematic diagram of the structure of graphene

图1. 石墨烯结构示意图

Figure 2. Schematic diagram of the structure of isolated carbon atom

图2. 孤立碳原子结构示意图

2.2. 计算过程及参数的选取

2.2.1. 石墨烯体系计算

对于石墨烯体系来说，选取C原子的2s2 2p2作为价电子，1s2作为芯电子；交换关联泛函采用了局域密度近似(LDA)；采用了平面波基组展开的方法，截断能量为280 eV；赝势采用了超软赝势(Ultra-soft potential)，为C_00.usp。对于k空间取样，采用了Monkhorst-Pack方法，grid size为10 * 6 * 1。共选取了30个k点。具体的计算参数如表1所示。

Table 1. Parameters of graphene total energy calculation

表1. 石墨烯总能量计算参数

2.2.2. 孤立碳原子体系计算

同样地，对于孤立碳原子来说，由于最终需要计算它和石墨烯体系能量的差值，因此尽量选取和石墨烯计算过程一致的参数，从而使二者的结果具有相对一致性，最终使差值更有意义。所以，选取C原子的2s2 2p2作为价电子，1s2作为芯电子；交换关联泛函采用了局域密度近似(LDA)；采用了平面波基组展开的方法，截断能量为280 eV；赝势采用了超软赝势(Ultra-soft potential)，为C_00.usp。对于k空间取样，采用了Monkhorst-Pack方法，共选取了1个k点(晶胞内只包含一个原子，因此只需对gamma点进行计算即可)，grid size为1 * 1 * 1。具体地计算参数如表2所示。

Table 2. Parameters of isolated carbon atom total energy calculation

表2. 孤立碳原子体系总能量计算参数

3. 计算结果和分析

如图3所示，对于石墨烯体系来说，经历了15步的自洽计算之后，单个原子总能量的变化(total energy/atom convergence)收敛到了0.1000E−05 eV，本征能量变化(eigen-energy convergence)收敛到了0.3333E−06 eV，最终得到的体系总能量为：

$\text{Finalenergy},E=-621.8196941698\text{eV}$ (8)

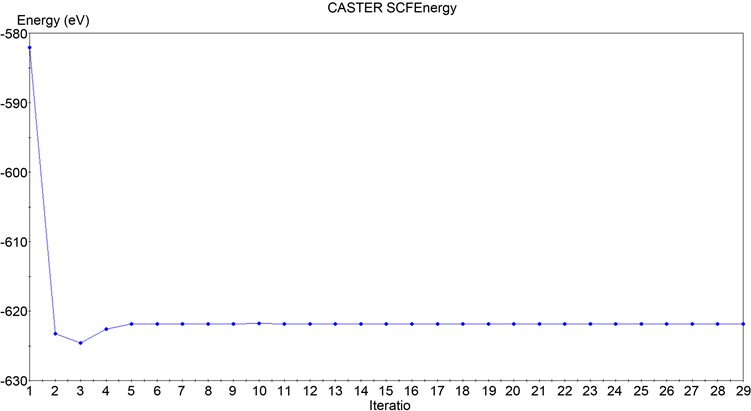
Figure 3. Convergence results of total graphene energy calculation

图3. 石墨烯总能量计算收敛结果

同样地，如图4所示，对于孤立的碳原子来说，经历了15步的自洽计算之后，单个原子总能量的变化(total energy/atom convergence)收敛到了0.1000E−05 eV，本征能量变化(eigen-energy convergence)收敛到了0.1667E−06 eV。最终得到的体系总能量为：

$\text{Finalenergy},E=-145.3495145913\text{eV}$ (9)

Figure 4. Convergence results of total isolated carbon atom energy calculation

图4. 孤立碳原子总能量计算收敛结果

对于上面计算得到的石墨烯体系总能量和孤立碳原子总能量，其绝对能量没有精确的物理意义，不同的参数选取和赝势对总能量的影响很大，但是对能量的差值来说，能取得较好的结果，因此，利用内聚能计算公式以及之前得到的结果，可以计算得到石墨烯体系的内聚能为：

$E=\frac{-621.8196941698\text{eV}-\left(-4\times 145.3495145913\text{eV}\right)}{4}\approx -10.105\text{eV}$ (10)

因此，得到的石墨烯内聚能为−10.105 eV。

相较于之前的计算过程不同的是，对于石墨烯体系，交换关联泛函采用了广义梯度近似中的PBE函数 [16]；得到的体系总能量为：

$\text{Finalenergy},E=-620.0817119187\text{eV}$ (11)

因此，结合之前得到的孤立碳原子的总能量，可以得到的石墨烯体系的内聚能为：

$E=\frac{-620.0817119187\text{eV}-\left(-4\times 145.3500139220\text{eV}\right)}{4}\approx -9.670414\text{eV}$ (12)

更进一步地，我们可以通过采用不同的交换关联泛函、提高K空间取点的个数、增加动能截断等方法，计算得到在不同参数下的石墨烯体系总能量，石墨烯和孤立碳原子体系的计算参数和结果分别如表3和表4所示。

Table 3. Calculation of the total energy of graphene under different parameters and methods

表3. 不同参数方法下的石墨烯的总能量计算

Table 4. Calculation of the total energy of isolated carbon atom under different parameters and methods

表4. 不同参数方法下的孤立碳原子的总能量计算

于是，即可共20组(5组石墨烯总能量计算 * 4组孤立碳原子总能量计算)不同参数及计算方法下的内聚能，例如，对于石墨烯体系取组4，对于孤立碳原子体系取组3，可得内聚能为−9.0720 eV。所以在不同的参数和计算方法下，得到的石墨烯的内聚能约为−9 eV到−10 eV。

4. 结果分析与讨论

总的来说，基于第一性原理和密度泛函理论，计算得到了石墨烯材料的内聚能。具体地，基组展开选取了平面波基组展开，赝势采用了模守恒赝势(Norm-conserving)以及超软赝势(Ultra-soft)，交换关联泛函采用了局域密度近似(LDA)以及广义梯度近似(GGA-PBE)，K空间取样采用了Monkhorst-Pack方法。

对于最终的结果来说，得到的内聚能大致在−9 eV到−10 eV。误差主要来自于交换关联项、赝势的选取、动能截断等等。因此，通过调整不同的交换关联泛函、选取不同的赝势、增加动能截断等方法，可以使得计算结果更加地精确。具体地，从表3和表4可以看出，对于石墨烯体系GGA计算得到的总能量相比LDA得到的更高，而对于孤立碳原子结构GGA计算得到的总能量比LDA得到的更低，这可能是因为，石墨烯结构较为致密，而孤立原子结构较为疏松，LDA计算致密结构的能量更接近于真实值，而疏松体系的能量偏大，而GGA相反，疏松结构的能量更接近于真实值，而致密结构则往往偏大。另一方面，对于石墨烯体系和孤立碳原子结构来说，采用模守恒势(NCP)相比于采用超软势(USP)来说，计算得到的总能量均更高。

通过进一步计算可以得到，用GGA计算得到的内聚能相比用LDA计算得到的内聚能更高(绝对值更低)，这可能是因为，GGA在计算孤立原子结构的总能量时偏低，但在计算石墨烯体系时偏高得更多，从而使得GGA得到的内聚能更高。

不同的计算方法和参数设置得到的结果有一定的差异，一方面，可以通过增加动能截断的能量，或者通过理论分析选取合适的方法或者参数，来提高计算结果的准确性；另一方面，未来也可以对比实验的结果，分析出哪种方法或者参数更加地适合石墨烯体系。未来可以将内聚能计算的方法推广到其它的新型量子材料中去，这对于研究新型材料的稳定性以及结构特性等有一定的理论指导意义。