一类系泊系统的设计问题

Design of a Class of Mooring Systems

摘要: 系泊系统的设计主要确定系泊系统各个部件的参数问题。本文把这些物理部件集中看成一点进行受力分析，分析这些部件之间的关系，各个部件处于什么状态下使整个系泊系统处于最优状态，根据静力平衡条件列出平衡方程，给出各个节点的坐标以及各个钢管和钢桶与竖直方向的夹角之间的关系方程，对锚链进行微元化，获得系泊系统状态下各个参数及位置关系，使系泊系统处于最优状态。

Abstract: The design of mooring system mainly determines the parameter problem of each component of mooring system. In this paper, we take these physical components as a point for force analysis, analyze the relationship between these components, make the whole mooring system in the optimal state under which state each component is in, and list the equilibrium equation according to the static equilibrium condition.

1. 引言

当今世界对石油资源的需求增大，海上石油资源开发已逐渐成为新的能源发展方向，因此，为了满足日益增长的能源需求，各国都将油气资源的开发的重点转移到深海。海上平台广泛应用于钻井，采油，加工处理和储存。为了保证海上平台在大多数海况下都可以正常工作，系泊系统的作用至关重要。因此，需要相关的理论来更好的解决相关设备中遇到的问题。目前有多种用于浮体结构定位的系泊系统，如果按系泊方式划分，可以分为悬链线锚腿系泊 [1] [2] [3]、单锚腿系泊 [4] [5] [6]、悬链线系泊 [7] [8] [9] [10] [11]、张力腿系泊 [12] [13] [14] [15] [16]、系缆桩–缓冲系泊 [17] - [23] 等。一般来说，系泊方式是根据系泊力的大小、水深、系索长度、是否配置中间浮体、地形和海床等条件来确定的。为适应深海平台开发的需要，近几年来，深海系泊理论和技术的研究得到了蓬勃发展。

一般近浅海平台观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。模型传输节点的浮标系统可简化为圆柱体。系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成，锚链选用无档普通链环，钢管共n节组成，水声通讯系统安装在密封圆柱形钢桶内。钢桶上接第n节钢管，下接电焊锚链。钢桶竖直时，水声通讯设备的工作效果最佳。若钢桶倾斜，则影响设备的工作效果。钢桶的倾斜角度(钢桶与竖直线的夹角)超过一定度时，设备的工作效果较差。为了控制钢桶的倾斜角度，钢桶与电焊锚链链接处可悬挂重物球。

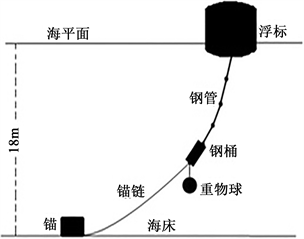
Figure 1. Transmission node diagram (structure module diagram only, size ratio not considered)

图1. 传输节点示意图(仅为结构模块示意图，未考虑尺寸比例)

在该系泊系统中，包括钢管、钢桶、重物球、电焊锚杆和特制的抗拖移锚组成。锚链末端与锚的连接处的切线方向与海床的夹角一般不超过β˚，否则，锚会被拖行。而钢桶的倾斜角度也被限制在0˚到α˚之间，0˚其工作效果最佳，倾斜角度愈大工作效果愈差，系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。关于系泊系统 [24] [25] [26] [27] [28] 有许多作者有研究，如潘斌 [14] 等研究了单腿浮标在外力作用下，其系泊系统的静力计算方法。系统包括：一个浮筒，一根锚泊线，一个锚。锚泊线可由多段不同重量和尺寸的索或链组成。计算中考虑了锚泊线的伸长变形以及流速沿水深的变化，孙宁松 [10] 对平台配备的定位锚泊系统进行分析和设计。

本文主要探讨了如何确定系泊系统浮标、钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚等参数，锚链选用无档普通链环，钢管共n节组成，水声通讯系统安装在密封圆柱形钢桶内。钢桶上接第n节钢管，下接电焊锚链。钢桶竖直时，在上述情况下如何确定参数使水声通讯设备的工作效果最佳问题。

2. 预备知识

为了能更好分析、描述系统个部件之间的相互影响，个部件的受力情况，不妨对个部件做如下的假设。

1) 假设钢管之间用铰链链接可自由转动。

2) 假设风是沿平行海平面的方向吹来。

3) 假设锚链和重物球的浮力影响可以忽略。

4) 假设忽略其它原因(如温度，湿度等)对系统影响。

5) 假设浮标不会出现因为风力等因素而被吹翻的情况。

为了讨论方便，钢管由4节组成依次把浮标、钢管(每节)、钢桶、重物球、猫链、猫的质量记作： $m_i\left(i=1,2,3,4,5,6\right)$，管对浮标的拉力与竖轴的夹角记作 ${\theta }_{10}$，钢管从上往下依次与竖轴的夹角记作 ${\theta }_{i+1i}\left(i=1,2,3\right)$，钢桶与竖轴的夹角 ${\theta }_{54}$，浮标高度为a；浮标的吃水深度为h；钢管长度为l；钢桶的高度为 $l_t$ ；锚链的长度为s。

3. 受力分析

浮标受的力由下几部分组成：在吃水深度为h的情况下浮标受到的浮力为 $f_{浮}=2Rh{\rho }_{水}g$ ；浮标所受海风的应力为 $f_{海}=0.625v^{2}2R\left(a-h\right)$ ；浮标自身的重力为 $m_{1}g$，将浮标、钢管、钢桶、重物球看成一个整体，整体受力分析，以浮力 $f_{浮}$ 方向向上看作y轴正向，海风应力 $f_{海}$ 与浮力垂直，看作x轴正向，钢管对浮标的作用力 $f_1$ 看作是外力，分解为x轴上的力 $f_{1x}$ 与y轴上的力 $f_{1y}$，系统整体受力平衡，因此有如下关系：

$f_{1x}=f_{海}$ (3.1)

$f_{1y}=f_{浮}-m_{1}g$ (3.2)

其中 $m_{1}g$ 为浮标的重力，当浮标的吃水深度为h，浮标的半径R，浮标的体积v及浮标的重力已知时，通过上方程计算得到钢管对浮标的作用力 $f_1$，当系泊系统处于平衡状态时，系统节点之间受到作用力与反作用力大小相等方向相反。从而钢管对浮标的作用力 $f_1$ 与浮标对钢管的拉力大小相等，方向相反。

3.1. 对钢桶受力情况进行分析

下面分析钢桶受力情况(如图2)，将各力直角系下的表示，钢桶受力有重物球的重力 $G_{球}=\left(0,-m_{4}g\right)$ ；钢桶的重力 $G_{桶}=\left(0,-m_{3}g\right)$ ；钢桶的浮力 $f_{桶}=\left(0,{\rho }_{水}{V}_{桶}g\right)$ ； $V_{桶}$ 是钢桶的体积，猫链的拉力 $f_{猫}=\left(-f_x,-f_y\right)$。力 $G_{球}+f_{猫}=\left(-f_x,-m_{4}g-f_y\right)$ 的作用点坐标为： $B\left(-l\sin \phi ,-l\cos \phi \right)$，l是桶的长度， $\phi$ 是桶的倾斜角；力 $G_{桶}+f_{桶}$ 的作用点坐标为： $A\left(-\frac{l}{2}\sin \phi ,-\frac{l}{2}\cos \phi \right)$ ；应用虚位移原理得：

$\left(G_{桶}+f_{桶}\right)\cdot {\delta }_A+\left(G_{球}+f_{猫}\right)\cdot {\delta }_B=0$ (3.3)

Figure 2. Steel barrel stress

图2. 钢桶受力

${\delta }_A=\left(-\frac{l}{2}\cos \phi \delta \phi ,\frac{l}{2}\sin \phi \delta \phi \right)$ ； ${\delta }_B=\left(-l\cos \phi \delta \phi ,l\sin \phi \delta \phi \right)$ 代入上方程(2.3)化简得：

$-\frac{l}{2}{m}_{3}g\sin \phi +\frac{l}{2}{\rho }_{水}{V}_{桶}g\sin \phi +l{f}_x\cos \phi -l{m}_{4}g\sin \phi -l{f}_y\sin \phi =0$ (3.4)

由此可解得 $\phi =\text{arctan}\frac{2f_x}{m_{3}g-{\rho }_{水}{V}_{桶}g+2m_{4}g+2f_y}$。

3.2. 对钢管进行受力分析

与浮标链接的钢管必然存在一对作用力与反作用力，两力大小相等方向相反，钢管与钢管链接处必然存在一对作用力与反作用力，两力大小相等方向相反；我们这里主要考虑它的力的大小对系统影响；不妨假设钢管、浮标均在一个平面内。

第一节钢管受力情况讨论：

第一节钢管的受力有：钢管的重力 $m_{2}g$ ；钢管的浮力 ${\rho }_{水}{V}_{管}g$ ；第二节对第一节钢管的拉力 $f_{21}=\left(f_{21x},f_{21y}\right)$ ；受力状况如图2所示：

钢管的重力与浮力可以看作集中在 $A\left(-\frac{k}{2}\sin {\theta }_1,-\frac{k}{2}\cos {\theta }_1\right)$ 点上，其中k为钢管的长度， ${\phi }_1$ 第一节钢管的倾斜角，A点受力 $\left(0,-m_{2}g+{\rho }_{水}{V}_{管}g\right)$ ； $B\left(-k\sin {\theta }_1,-k\cos {\theta }_1\right)$ 是第二与第一节钢管的接点，B点受力 $f_{21}=\left(f_{21x},f_{21y}\right)$ ； $V_{管}$ 是钢管的体积，应用虚位移原理得：

$\left(0,-m_{2}g+{\rho }_{水}{V}_{管}g\right)\cdot {\delta }_A+\left(f_{21x},f_{21y}\right)\cdot {\delta }_B=0$ (3.5)

${\delta }_A=\left(-\frac{k}{2}\cos {\theta }_1\delta {\theta }_1,\frac{k}{2}\sin {\theta }_1\delta {\theta }_1\right)$ ； ${\delta }_B=\left(-k\cos {\theta }_1\delta {\theta }_1,k\sin {\theta }_1\delta {\theta }_1\right)$ 代入上方程化简得：

$-\frac{k}{2}{m}_{2}g\sin {\theta }_1\delta {\theta }_1+\frac{k}{2}{\rho }_{水}{V}_{管}g\sin {\theta }_1\delta {\theta }_1-k{f}_{21x}\cos {\theta }_1\delta {\theta }_1+k{f}_{21y}\sin {\theta }_1\delta {\theta }_1=0$ (3.6)

由此可解得 ${\theta }_1=\arctan \frac{2k{f}_{21x}}{-k{m}_{2}g+k{\rho }_{水}{V}_{管}g+2k{f}_{21y}}$。

第二节钢管受力情况讨论：

第二节钢管的受力有，钢管的重力 $m_{2}g$ ；钢管的浮力 ${\rho }_{水}{V}_{管}g$ ；第三节对第二节钢管的拉力 $f_{32}=\left(f_{32x},f_{32y}\right)$ 受力状况，钢管的重力与浮力可以看作集中在 $A\left(-\frac{k}{2}\sin {\theta }_2,-\frac{k}{2}\cos {\theta }_2\right)$ 点上，其中k为钢管的长度， ${\phi }_2$ 第二节钢管的倾斜角，A点受力 $\left(0,-m_{2}g+{\rho }_{水}{V}_{管}g\right)$ ； $B\left(-k\sin {\theta }_2,-k\cos {\theta }_2\right)$ 是第三与第二节钢管的接点，B点受力 $f_{32}=\left(f_{32x},f_{32y}\right)$ ；受力状况类似如图2所示，应用虚位移原理得：

$\left(0,-m_{2}g+{\rho }_{水}{V}_{管}g\right)\cdot {\delta }_A+\left(f_{32x},f_{32y}\right)\cdot {\delta }_B=0$ (3.7)

${\delta }_A=\left(-\frac{k}{2}\cos {\theta }_2\delta {\theta }_2,\frac{k}{2}\sin {\theta }_2\delta {\theta }_2\right)$ ； ${\delta }_B=\left(-k\cos {\theta }_2\delta {\theta }_2,k\sin {\theta }_2\delta {\theta }_2\right)$ 代入上方程化简得：

$-\frac{k}{2}{m}_{2}g\sin {\theta }_2\delta {\theta }_2+\frac{k}{2}{\rho }_{水}{V}_{管}g\sin {\theta }_2\delta {\theta }_2-k{f}_{32x}\cos {\theta }_2\delta {\theta }_2+k{f}_{32y}\sin {\theta }_2\delta {\theta }_2=0$ (3.8)

由此方程可解得 ${\theta }_2=\arctan \frac{2k{f}_{32x}}{-k{m}_{2}g+k{\rho }_{水}{V}_{管}g+2k{f}_{32y}}$

第三节钢管受力情况讨论：

第三节钢管的受力有，钢管的重力 $m_{2}g$ ；钢管的浮力 ${\rho }_{水}{V}_{管}g$ ；第四节对第三节钢管的拉力 $f_{43}=\left(f_{43x},f_{43y}\right)$，第三节受力：钢管的重力与浮力可以看作集中在 $A\left(-\frac{k}{2}\sin {\theta }_3,-\frac{k}{2}\cos {\theta }_3\right)$ 点上，其中k为钢管的长度， ${\phi }_3$ 第三节钢管的倾斜角，A点受力 $\left(0,-m_{3}g+{\rho }_{水}{V}_{管}g\right)$ ； $B\left(-k\sin {\theta }_3,-k\cos {\theta }_3\right)$ 是第四与第三节钢管的接点，B点受力 $f_{43}=\left(f_{43x},f_{43y}\right)$ ；受力状况类似如图2所示，应用虚位移原理得：

$\left(0,-m_{2}g+{\rho }_{水}{V}_{管}g\right)\cdot {\delta }_A+\left(f_{43x},f_{43y}\right)\cdot {\delta }_B=0$ (3.9)

${\delta }_A=\left(-\frac{k}{2}\cos {\theta }_3\delta {\theta }_3,\frac{k}{2}\sin {\theta }_3\delta {\theta }_3\right)$ ； ${\delta }_B=\left(-k\cos {\theta }_3\delta {\theta }_3,k\sin {\theta }_3\delta {\theta }_3\right)$ 代入上方程化简得：

$-\frac{k}{2}{m}_{2}g\sin {\theta }_3\delta {\theta }_3+\frac{k}{2}{\rho }_{水}{V}_{管}g\sin {\theta }_3\delta {\theta }_3-k{f}_{43x}\cos {\theta }_3\delta {\theta }_3+k{f}_{43y}\sin {\theta }_3\delta {\theta }_3=0$ (3.10)

由此方程可解得： ${\theta }_3=\arctan \frac{2k{f}_{43x}}{-k{m}_{2}g+k{\rho }_{水}{V}_{管}g+2k{f}_{43y}}$

第四节钢管受力情况讨论：

第四节钢管的受力有，钢管的重力 $m_{2}g$ ；钢管的浮力 ${\rho }_{水}{V}_{管}g$ ；钢桶对第四节钢管的拉力 $f_4=\left(f_{4x},f_{4y}\right)$，第四节受力：钢管的重力与浮力可以看作集中在 $A\left(-\frac{k}{2}\sin {\theta }_4,-\frac{k}{2}\cos {\theta }_4\right)$ 点上，其中k为钢管的长度， ${\phi }_4$ 第四节钢管的倾斜角，A点受力 $\left(0,-m_{3}g+{\rho }_{水}{V}_{管}g\right)$ ； $B\left(-k\sin {\theta }_4,-k\cos {\theta }_4\right)$ 是钢桶与第三节钢管的接点，B点受力 $f_4=\left(f_{4x},f_{4y}\right)$ ；受力状况类似如图2所示，应用虚位移原理得：

$\left(0,-m_{2}g+{\rho }_{水}{V}_{管}g\right)\cdot {\delta }_A+\left(f_{4x},f_{4y}\right)\cdot {\delta }_B=0$ (3.11)

${\delta }_A=\left(-\frac{k}{2}\cos {\theta }_4\delta {\theta }_4,\frac{k}{2}\sin {\theta }_4\delta {\theta }_4\right)$ ； ${\delta }_B=\left(-k\cos {\theta }_4\delta {\theta }_4,k\sin {\theta }_4\delta {\theta }_4\right)$ 代入上方程化简得：

$-\frac{k}{2}{m}_{2}g\sin {\theta }_4\delta {\theta }_4+\frac{k}{2}{\rho }_{水}{V}_{管}g\sin {\theta }_4\delta {\theta }_4-k{f}_{4x}\cos {\theta }_4\delta {\theta }_4+k{f}_{4y}\sin {\theta }_4\delta {\theta }_4=0$ (3.12)

由此方程可解得 ${\theta }_4=\arctan \frac{2k{f}_{4x}}{-k{m}_{2}g+k{\rho }_{水}{V}_{管}g+2k{f}_{4y}}$

3.3. 对锚链进行受力分析

锚链在水中必然是呈弯曲状态，在平衡状态下锚链的形状为一悬链线，是双曲余弦函数，最低点处受水平向左的拉力H，右悬挂点处受一个斜向上的拉力T，设T和水平方向夹角为 $\theta$，锚链的质量为 $m_5$，锚链的线密度为 ${\rho }_l$，s为锚链的长度，则猫链的重力为 $G={\rho }_{l}s$，设猫链上任意一点上的切线的切角为 $\theta$，

根据力学原理可知，H、G和T三力平衡，可知 $\tan \theta =\frac{G}{H}$，假设水平张力在猫链上处处相等，对于任意一段猫链 $l_s$，该平衡均成立， $\tan \theta =\frac{{\rho }_l{l}_s}{H}$，而 $\tan \theta =\frac{\text{d}y}{\text{d}x}$，对该式 $\tan \theta =\frac{{\rho }_l{l}_s}{H}$ 取微分，则有

$\text{d}\left(\tan \theta \right)=\frac{{\rho }_l}{H}\text{d}\left(l_s\right)=\frac{{\rho }_l}{H}\sqrt{{\left(\text{d}x\right)}^2+{\left(\text{d}y\right)}^2}=\frac{{\rho }_l}{H}\sqrt{1+{\left(\tan \theta \right)}^2}\text{d}x$ (3.13)

对方程(2.13)两边积分得

${\displaystyle \int \frac{d\left(\tan \theta \right)}{\sqrt{1+{\left(tan\theta \right)}^2}}}={\displaystyle \int \frac{{\rho }_l}{H}\text{d}x}$ (3.14)

解此方程得悬链线的一般方程为

$y=\frac{{\rho }_l}{H}ch\left(\frac{{\rho }_l}{H}x+c_1\right)+c_2$ (3.15)

由初始条件：猫链拖地，并设拖地点为原点，则对于拖地点有 $x=0,y=0,\tan \theta =0$ 代入悬链线的一般方程得 $c_1=0,c_2=\frac{{\rho }_l}{H}$，则猫链的方程

$y=\frac{{\rho }_l}{H}ch\left(\frac{{\rho }_l}{H}x+1\right)$ (3.16)

根据题中给出的参考图，我们不妨把他们看成在一个平面内，以猫为坐标原点，海底为x轴，与海底垂直向上为y轴，我们假设浮标吃水深度为h，第i根钢管的倾斜角为 ${\theta }_i\left(i=1,2,3,4\right)$， ${\theta }_4$ 为钢桶的倾斜角， ${\theta }_5$ 为猫链与钢桶连接处悬链线的切线的夹角， $f_{i+1i}\left(i=0,1,2,3,4,5\right)$ 为第 $i+1$ 根钢管对i根钢管的拉力，为了表达方便把浮标、钢桶、猫也看成钢管， $i=0$ 对应浮标。当系泊系统处于平衡状态是，水平方向与垂直方向的合力为零，我们把浮标、钢管、钢桶、重力球、猫链、猫所受力分解为水平方向与垂直方向得到平衡方程，求解方程得到系泊系统各个参数，得到问题的解。

1) 浮标受力情况

浮标受到的浮力为： $f_{浮}=2Rh{\rho }_{水}g$。

浮标所受海风的应力为： $f_{海}=0.625v^{2}2R\left(a-h\right)$。

浮标自身的重力为： $m_{1}g$。

与钢管连接处钢管的拉力 $f_{10}=\left(f_{10x},f_{10y}\right)$。

系泊系统处于平衡状态时，水平与垂直方向上合力为零。

即得平衡方程 $\{\begin{array}{l}{f}_{浮}-m_{1}g-f_{10y}=0\\ f_{海}-f_{10x}=0\end{array}$。

2) 钢管受力情况

当系泊系统处于平衡状态时，根据物理力学知识，每个节点上作用力与反作用力大小相等，方向相反，每个节点上力矩总和为零。

第一节钢管受力分析，把第一节钢管与浮标连接处看成相对转动点，浮标对第一节钢管的拉力 $-f_{10}=\left(-f_{10x},-f_{10y}\right)$ ；钢管自身的重力为 $m_{2}g$ ；钢管的浮力为 ${\rho }_{水}{V}_{管}g$ ；第二节钢管对第一节钢管的拉力 $f_{2,1}=\left(f_{2,1x},f_{2,1y}\right)$ ；则这点受力方程式及力矩平衡方程

$\{\begin{array}{l}-f_{10x}-f_{21x}=0\\ -f_{10y}-f_{21y}-m_{2}g+{\rho }_{水}{V}_{管}g=0\end{array}$ $f_{21}\sin \left({\theta }_2-{\theta }_1\right)+\left({\rho }_{水}{V}_{管}g-m_{2}g\right)\sin {\theta }_1=0$。

第二节钢管受力情况类似

$\{\begin{array}{l}-f_{21x}-f_{32x}=0\\ -f_{21y}-f_{32y}-m_{2}g+{\rho }_{水}{V}_{管}g=0\end{array}$ $f_{32}\sin \left({\theta }_3-{\theta }_2\right)+\left({\rho }_{水}{V}_{管}g-m_{2}g\right)\sin {\theta }_2=0$

第三节钢管受力情况类似

$\{\begin{array}{l}-f_{32x}-f_{43x}=0\\ -f_{32y}-f_{43y}-m_{2}g+{\rho }_{水}{V}_{管}g=0\end{array}$ $f_{43}\sin \left({\theta }_4-{\theta }_3\right)+\left({\rho }_{水}{V}_{管}g-m_{2}g\right)\sin {\theta }_3=0$

第四节钢管受力情况类似

$\{\begin{array}{l}-f_{43x}-f_{54x}=0\\ -f_{43y}-f_{54y}-m_{2}g+{\rho }_{水}{V}_{管}g=0\end{array}$ $f_{54}\sin \left({\theta }_5-{\theta }_4\right)+\left({\rho }_{水}{V}_{管}g-m_{2}g\right)\sin {\theta }_4=0$

钢桶受力情况类似

$\{\begin{array}{l}-f_{54x}-f_{65x}=0\\ -f_{54y}-f_{65y}-m_{3}g-m_{4}g+{\rho }_{水}{V}_{桶}g=0\end{array}$

浮标的吃水深度为h，则当系泊系统处于平衡状态时，系泊系统位于水下部分的深度为

$L=h+l\left(\cos {\theta }_1+\cos {\theta }_2+\cos {\theta }_3+\cos {\theta }_4\right)+l_t\cos {\theta }_5+s_y$ (3.17)

其中 $s_y$ 锚链在水中的深度；当系泊系统处于平衡状态时，根据前面受力分析，利用每个节点之间作用力与反作用力之间的关系，从浮标出发考虑问题，当浮标的吃水深度为h等参数确定时，利用力学原理及平衡状态下课计算确定上述参数 ${\theta }_i\left(i=1,\cdots ,5\right)$ ；因此我们下面只要确定锚链在水中的深度 $s_y$ 即可，而猫链在水中

的方程是 $y=\frac{{\rho }_l}{H}ch\left(\frac{{\rho }_l}{H}x+1\right)$，只要确定猫链与钢桶的连接点坐标， $s_y$ 的大小即可确定。因此只要确定海水

的深度，根据我们给出的模型，就可计算、模拟出系泊系统各项部件的参数要求，从而设计一套系泊系统。

本文着重分析了浮标、钢管、钢桶、重物球、猫链之间的受力关系及相互之间的影响，建立了它们之间受力方程。建立了猫链的曲线方程，得到只要确定海水深度，就可确定各部件在给定的条件下的参数，但各根钢管、猫链的张力分配问题没有考虑，需后续进一步讨论，其特点在工程设计中，类似的问题根据给出的设备情况可以参考该模型，其优势具有一定的通用参考价值，可以引用模型分析具体问题。特别是对每个部件的受力分析及部件之间的衔接分析对类似问题可引用。

4. 总结与展望

本文对系泊系统组成的各个部件参数进行了探究，通过悬链线理论 [11] 对部件及部件之间的受力进行分析，获得：1) 各个部件级部件之间的关系方程表达式，2) 部件之间受力方程，3) 锚链的方程表达式，通过方程优化在一定条件下得到这类系泊系统的各个物理参数。下一步需对这些参数及部件需要进一步优化、修改，同时要综合考虑风力、水流力等复杂情况下系泊系统设计，本文从数学角度进行分析，与实际情况有差异，望后续继续分析改进。

参考文献