球域上椭圆方程有效的有限元方法和误差分析

An Effective Finite Element Method and Error Analysis for the Elliptic Equation in Spherical Domain

摘要: 本文提出了一种有效的有限元方法来求解球域上的椭圆方程。首先，利用球坐标变换和球谐函数展开，将原问题化为一系列等价的一维问题。其次，通过引入带权的Sobolev空间，建立了每个一维问题的弱形式和相应的离散形式。另外，利用分片线性插值多项式的逼近性质证明了逼近解的误差估计。最后给出了算法的具体实现过程，并通过数值例子验证了算法的有效性。

Abstract: In this paper, an effective finite element method is proposed to solve the elliptic equation in spherical domain. Firstly, a series of one-dimensional problems equivalent to the original problem are derived by introducing spherical coordinate transformation and using spherical harmonic functions expansion. Secondly, we introduce a weighted Sobolev space and establish the weak form and the corresponding discrete scheme. In addition, by using the approximation properties of piecewise linear interpolation polynomials, the error estimates of approximation solutions are proved. Finally, the concrete process of implementing the algorithm is given, and the effectiveness of the algorithm is verified by numerical experiments.

1. 引言

有限元方法是求解微分方程常用的数值方法之一，具有数值稳定性、通用性强的特点。其思想是利用变分原理，通过构造有限维空间中的分片多项式函数来逼近原问题的真解。计算机的出现，使得有限元法在很多方面得到广泛应用，例如：物理学、材料科学、生物学(参见文献 [1] - [9] )等。

关于求解二阶椭圆方程的数值方法有很多，主要包括弱有限元法，即在多边形或多面体网格区域上求解二阶椭圆问题(参见文献 [10] [11] [12] [13] )、有限体积法和谱方法(参见文献 [12] [13] [14] [15] )等。然而，却很少在于球域上研究椭圆方程，主要是直接在球域上通过网格剖分构造基函数比较复杂和困难。

因此，本文提出了一种有效的有限元方法来求解球域上的椭圆方程。首先，利用球坐标变换和球谐函数展开，将原问题化为一系列等价的一维问题。其次，通过引入带权的Sobolev空间，建立了每个一维问题的弱形式和相应的离散形式。另外，利用分片线性插值多项式的逼近性质证明了逼近解的误差估计。最后给出了算法的具体实现过程，并通过数值例子验证了算法的有效性。

最后，简要介绍本文接下来的工作安排。在第2节，我们推导了原问题的降维格式。在第3节，引入带权的Sobolev空间，推导原问题基于降维格式的弱形式和相对应的离散格式。在第4节，证明逼近解的误差估计。在第5节，给出了该算法的具体实现过程。在第6节，提供了一些数值例子验证算法的有效性。最后，在第7节，给出了一些结论性评注。

2. 降维格式

作为模型问题，我们考虑下面的二阶椭圆方程：

$\{\begin{array}{l}-\Delta u+\alpha u=f,x\in \Omega ,\\ u=0,x\in \partial \Omega ,\end{array}$ (2.1)

其中， $\Omega =\left\{\left(x,y,z\right)\in R^3:x^2+y^2+z^2<R\right\}$，n是边界 $\partial \Omega$ 的单位外法向量。

为了有效地求解该问题，我们将利用球坐标变换和球谐函数展开，将原问题化为一系列等价的一维问题。定义如下的微分算子：

$\mathcal{L}v=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial v}{\partial r}\right)+\frac{1}{r^2}{\Delta }_{s}v$ (2.2)

其中

${\Delta }_s=\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial }{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2}{\partial {\varphi }^2}$

由格林公式可知，(2.1)的弱形式为：找 $u\in H_0^1\left(\Omega \right)$，使得

${\displaystyle {\int }_{\Omega }\nabla }u\nabla \bar{v}\text{d}x\text{d}y\text{d}z+\alpha {\displaystyle {\int }_{\Omega }u}\bar{v}\text{d}x\text{d}y\text{d}z={\displaystyle {\int }_{\Omega }f}\bar{v}\text{d}x\text{d}y\text{d}z$， $\forall v\in H_0^1\left(\Omega \right)$ (2.3)

其中 $\bar{v}$ 是v的复共轭。则由球坐标变化 $x=r\sin \theta \cos \varphi ,y=r\sin \theta \sin \varphi ,z=r\cos \theta$ 可得到(2.1)在球坐标系下的方程为：

(2.4)

$\phi \left(R,\theta ,\varphi \right)=0$ (2.5)

其中 $\phi \left(r,\theta ,\varphi \right)=u\left(x,y,z\right)$， $g\left(r,\theta ,\varphi \right)=f\left(x,y,z\right)$，。

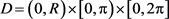由(2.3)可得到(2.4)，(2.5)的弱形式为：

$a\left(\phi ,\psi \right)=\left(g,\psi \right)$ (2.6)

其中

$a\left(\phi ,\psi \right)={\displaystyle {\int }_0^R{\displaystyle {\int }_{\mathcal{S}}{r}^2}}\mathcal{L}\phi \bar{\psi }\text{d}r\text{d}S+\alpha {\displaystyle {\int }_0^R{\displaystyle {\int }_{\mathcal{S}}{r}^2}}\phi \bar{\psi }\text{d}r\text{d}S$

$\left(g,\psi \right)={\displaystyle {\int }_0^R{\displaystyle {\int }_{\mathcal{S}}{r}^{2}g}}\bar{\psi }\text{d}r\text{d}S$

其中S是单位球面。令 $\phi \left(r,\theta ,\varphi \right)={\displaystyle \underset{\left|m\right|=0}{\overset{\infty }{\sum }}{\displaystyle \underset{\left|l\right|=0}{\overset{m}{\sum }}{\phi }_m^l}}{Y}_m^l$， $g\left(r,\theta ,\varphi \right)={\displaystyle \underset{\left|m\right|=0}{\overset{\infty }{\sum }}{\displaystyle \underset{\left|l\right|=0}{\overset{m}{\sum }}{g}_m^l}}{Y}_m^l$，其中 $Y_m^l$ 表示球调和函数，且具

有如下性质：

${\Delta }_s{Y}_m^l=-m\left(m+1\right)Y_m^l$， $m\ge 0$， $\left|l\right|\le m$， ${\displaystyle {\int }_S{Y}_m^l}{Y}_{m^{\prime }}^{l^{\prime }}\text{d}S={\sigma }_{m{m}^{\prime }}{\sigma }_{l{l}^{\prime }}$ (2.7)

令 $l_{m}v=\frac{1}{r^2}{\left(r^2{v}_r\right)}_r-\frac{m\left(m+1\right)}{r^2}v$，则由球调和函数的性质(2.7)可知(2.4)和(2.5)

等价于如下的一系列一维问题：

$-l_m{\phi }_m+\alpha {\phi }_m=g_m\left(r\right)$， $r\in \left(0,R\right)$ (2.8)

${\phi }_m^l\left(R\right)=0$ (2.9)

令 $r=Rt$， $u_m^l\left(t\right)={\phi }_m^l\left(Rt\right)$， $F_m^l\left(t\right)=g_m^l\left(Rt\right)$， ${\mathcal{L}}_{m}v=\frac{1}{t^2}{\left(t^2{v}_t\right)}_t-\frac{m\left(m+1\right)}{t^2}v$，则(2.8)~(2.9)等价为：

$-{\mathcal{L}}_m{u}_m^l+\alpha R^2{u}_m^l=R^2{F}_m^l$， $t\in \left(0,1\right)$ (2.10)

$u_m^l\left(1\right)=0$ (2.11)

3. 弱形式和离散格式

首先，我们引入通常的带权Sobolev空间：

$L_{\omega }^2\left(I\right):=\left\{f:{\displaystyle {\int }_I\omega }{f}_m^2\text{d}t<\infty \right\}$

相应的内积和范数分别为：

${\left(f_m,g_m\right)}_{\omega }={\displaystyle {\int }_I\omega }{f}_m{g}_m\text{d}t$， ${\Vert f_m\Vert }_{\omega }={\left({\displaystyle {\int }_I\omega }{f}_m^2\text{d}t\right)}^{\frac{1}{2}}$

其中 $I=\left(0,1\right)$， $\omega =x^2$ 为权函数。然后定义非一致带权Sobolev空间：

$\begin{array}{l}{H}_{0,\omega ,0}^1\left(I\right):=\left\{u_0^l:{\partial }_t^k{u}_0^l\in L_{\omega }^2\left(I\right),u_0^l\left(1\right)=0,k=0,1\right\},m=0;\\ H_{0,\omega ,m}^1\left(I\right):=\left\{u_m^l:{\partial }_t^k{u}_m^l\in L_{{\omega }^k}^2\left(I\right),u_m^l\left(1\right)=0,k=0,1\right\},m\ge 1\end{array}$

其相对应的内积和范数分别为：

$\begin{array}{l}{\left(f_{\text{0}}^l,g_{\text{0}}^l\right)}_{1,\omega ,\text{0}}={\displaystyle \underset{k=0}{\overset{1}{\sum }}{\left({\partial }_t^k{f}_{\text{0}}^l,{\partial }_t^k{g}_{\text{0}}^l\right)}_{\omega }},{\Vert f_{\text{0}}^l\Vert }_{1,\omega ,\text{0}}={\left(f_{\text{0}}^l,f_{\text{0}}^l\right)}_{1,\omega ,\text{0}}^{\frac{1}{2}};\\ {\left(f_m^l,g_m^l\right)}_{1,\omega ,m}={\displaystyle \underset{k=0}{\overset{1}{\sum }}{\left({\partial }_t^k{f}_m^l,{\partial }_t^k{g}_m^l\right)}_{{\omega }^k}},{\Vert f_m^l\Vert }_{1,\omega ,m}={\left(f_m^l,f_m^l\right)}_{1,\omega ,m}^{\frac{1}{2}}\end{array}$

则方程(2.10)~(2.11)的弱形式为：找 $u_m^l\in H_{0,\omega ,m}^1\left(I\right)$，使得

$a_m\left(u_m^l,v\right)=F_m\left(v\right)$， $\forall v\in H_{0,\omega ,m}^2\left(I\right)$ (3.1)

其中：

$a_m\left(u_m^l,v\right)={\displaystyle {\int }_I{t}^2}{\left(u_m^l\right)}^{\prime }{v}^{\prime }+m\left(m+1\right)u_m^{l}v\text{d}t+\alpha R^2{\displaystyle {\int }_I{t}^2}{u}_m^{l}v\text{d}t$，

$F_m\left(v\right)=R^2{\displaystyle {\int }_I{t}^2}{F}_m^{l}v\text{d}t$。

取逼近空间 $X_{mh}=U_h\cap H_{0,\omega ,m}^1\left(I\right)$，其中 $U_h$ 是由分段线性插值基函数组成的空间，则(3.1)相对应的离散格式为：找 $u_{mh}^l\in X_{mh}$，使得

$a_m\left(u_{mh}^l,v_{mh}^l\right)=F_m\left(v_{mh}^l\right)$， $\forall v_{mh}^l\in X_{mh}$ (3.2)

4. 误差估计

为了简洁起见，我们使用表达式 $a\lesssim b$ 或 $a\gtrsim b$ 来表示存在一个正常数C使得 $a\le Cb$ 或 $a\ge Cb$。

定理1. 双线性形式 $a_m\left(u_m^l,v\right)$ 在 $H_{0,\omega ,m}^1\left(I\right)\times H_{0,\omega ,m}^1\left(I\right)$ 上是有界且正定的，即：

$\left|a_m\left(u_m^l,v\right)\right|\lesssim {\Vert u_m^l\Vert }_{0,\omega ,m}{\Vert v\Vert }_{0,\omega ,m}$，

$a_m\left(u_m^l,u_m^l\right)\gtrsim {\Vert u_m^l\Vert }_{0,\omega ,m}^2$。

证明：由Cauchy-Schwarz不等式我们可得：

$\begin{array}{c}\left|a_m\left(u_m^l,v\right)\right|=\left|{\displaystyle {\int }_I{t}^2}{\left(u_m^l\right)}^{\prime }{v}^{\prime }+m\left(m+1\right)u_m^{l}v\text{d}t+\alpha R^2{\displaystyle {\int }_I{t}^2}{u}_m^{l}v\text{d}t\right|\\ \lesssim {\displaystyle {\int }_I{t}^2}\left|{\left(u_m^l\right)}^{\prime }{v}^{\prime }\right|+m\left(m+1\right)\left|u_m^{l}v\right|+t^2\left|u_m^{l}v\right|\text{d}t\\ \lesssim {\left[{\displaystyle {\int }_I{t}^2{\left[{\left(u_m^l\right)}^{\prime }\right]}^2+t^2{\left(u_m^l\right)}^2+m\left(m+1\right){\left(u_m^l\right)}^2\text{d}t}\right]}^{\frac{1}{2}}{\left[{\displaystyle {\int }_I{t}^2{\left(v^{\prime }\right)}^2+t^2{v}^2+m\left(m+1\right)v^2\text{d}t}\right]}^{\frac{1}{2}}\\ \lesssim {\Vert u_m^l\Vert }_{0,\omega ,m}{\Vert v\Vert }_{0,\omega ,m}\end{array}$

$a_m\left(u_m^l,u_m^l\right)={\displaystyle {\int }_I{t}^2}{\left[{\left(u_m^l\right)}^{\prime }\right]}^2+m\left(m+1\right){\left(u_m^l\right)}^2\text{d}t+\alpha R^2{\displaystyle {\int }_I{t}^2}{\left(u_m^l\right)}^2\text{d}t\gtrsim {\Vert u_m^l\Vert }_{0,\omega ,m}^2$

定理2. 如果 $F_m\left(t\right)\in L_{\omega }^2\left(I\right)$，则 $F_m\left(v\right)$ 为 $H_{0,\omega ,m}^1\left(I\right)$ 上的有界线性泛函，即：

$\left|F_m\left(v\right)\right|\lesssim {\Vert v\Vert }_{0,\omega ,m}$。

证明：由Cauchy-Schwarz不等式有

$\begin{array}{c}\left|F_m\left(v\right)\right|=\left|{\displaystyle {\int }_I{t}^2}{F}_m^{l}v\text{d}x\right|=\left|{\displaystyle {\int }_I\left(t{F}_m^l\right)}\left(tv\right)\text{d}t\right|\lesssim {\left[{\displaystyle {\int }_I{\left(t{F}_m^l\right)}^2\text{d}t}\right]}^{\frac{1}{2}}{\left[{\displaystyle {\int }_I{\left(tv\right)}^2\text{d}t}\right]}^{\frac{1}{2}}\\ \lesssim {\left[{\displaystyle {\int }_I{\left(tv\right)}^2\text{d}t}\right]}^{\frac{1}{2}}\lesssim {\left[{\displaystyle {\int }_I{\left(t{v}^{\prime }\right)}^2+{\left(tv\right)}^2}\text{d}t\right]}^{\frac{1}{2}}={\Vert v\Vert }_{0,\omega ,m}\end{array}$

则由定理1，定理2和Lax-milgram定理我们有下面的定理：

定理3. 若 $F_m^l\in L_{\omega }^2\left(I\right)$，方程(3.1) 和(3.2)分别存在唯一解 $u_m^l\in H_{0,\omega ,m}^1\left(I\right)$ 和 $u_{mh}^l\in X_{mh}$。

定义区间I上的插值投影 $I_h{u}_m^l$ ： $H_{0,\omega ,m}^1\left(I\right)\to U_h$，由文献 [16] 中的分段线性插值理论可得如下引理。

引理1. 对于 $u_m^l\in H_{0,\omega ,m}^1\left(I\right)$，若 $u_m^l\left(x\right)$ 在区间I上有连续导数，则成立：

${\Vert I_h{u}_m^l-u_m^l\Vert }_{0,\omega ,m}\lesssim h$。

定理4. 假设 $u_m$ 和 $u_{mh}$ 分别是方程(3.1)和(3.2)的解，则下列不等式成立：

${\Vert u_m^l-u_{mh}^l\Vert }_{0,\omega ,m}\lesssim h$。

证明：由(3.1) 和(3.2)我们可得

$a_m\left(u_m^l,v_h\right)=F_m\left(v_h\right)$， $\forall v_h\in X_{mh}$ (4.1)

$a_m\left(u_{mh}^l,v_h\right)=F_m\left(v_h\right)$， $\forall v_h\in X_{mh}$ (4.2)

因此

$a_m\left(u_m^l-u_{mh}^l,v_h\right)=0$ (4.3)

结合定理1和(4.3)可得

$\begin{array}{c}{\Vert u_m^l-u_{mh}^l\Vert }_{0,\omega ,m}^2\lesssim a_m\left(u_m^l-u_{mh}^l,u_m^l-u_{mh}^l\right)\\ =a_m\left(u_m^l-u_{mh}^l,u_m^l+v_h-v_h-u_{mh}^l\right)\\ =a_m\left(u_m^l-u_{mh}^l,u_m^l-v_h\right)\\ \lesssim {\Vert u_m^l-u_{mh}^l\Vert }_{0,\omega ,m}{\Vert u_m^l-v_h\Vert }_{0,\omega ,m}\end{array}$

则有

${\Vert u_m^l-u_{mh}^l\Vert }_{0,\omega ,m}\lesssim \underset{v_h\in X_{mh}}{\inf }{\Vert u_m^l-v_h\Vert }_{0,\omega ,m}$ (4.4)

结合(4.4)和引理1可得

${\Vert u_m^l-u_{mh}^l\Vert }_{0,\omega ,m}\lesssim h$.

5. 算法的有效实施

为了更好的验证我们算法的有效性，我们构造满足边值条件的基函数如下：

${\phi }_0\left(t\right)=\{\begin{array}{l}1-\frac{t-t_0}{h_1}，t_0\le t\le t_1,\\ 0，其它，\end{array}$ (5.1)

${\phi }_i(t)=\{\begin{array}{l}1+\frac{t-t_i}{h_i},t_{i-1}\le t\le t_i,\\ 1-\frac{t-t_i}{h_{i+1}},t_i\le t\le t_{i+1},\\ 0,其它,\end{array}$ (5.2)

其中 $i=1,\cdots ,N-1$。则逼近空间可取为：

$X_h\left(m\right)=\text{span}\left\{{\phi }_0\left(t\right),{\phi }_1\left(t\right),\cdots ,{\phi }_{N-1}\left(t\right)\right\}$。

设

$\begin{array}{l}{a}_{ij}^m={\displaystyle {\int }_I{t}^2}{{\phi }^{\prime }}_j{{\phi }^{\prime }}_i\text{d}t,b_{ij}^m=m\left(m+1\right){\displaystyle {\int }_I{\phi }_j}{\phi }_i\text{d}t,\\ c_{ij}^m=\alpha R^2{\displaystyle {\int }_I{t}^2{\phi }_j}{\phi }_i\text{d}t,f_{ij}^m=R^2{\displaystyle {\int }_I{t}^2{F}_m^l}{\phi }_j\text{d}t\end{array}$

令

$u_{mh}={\displaystyle \underset{i=0}{\overset{N-1}{\sum }}{u}_i^m}{\phi }_i\left(t\right)$ (5.3)

将(5.3)式代入(3.2)式，把 $v_{mh}$ 取遍逼近空间 $X_h\left(m\right)$ 中的所有基函数，即可得如下的线性系统：

$\left(A+B+C\right)U^m=G^m$ (5.4)

其中

$A=\left(a_{ij}^m\right)$， $B=\left(b_{ij}^m\right)$， $C=\left(c_{ij}^m\right)$， $G=\left(f_{ij}^m\right)$， $U^m={\left(u_0^m,u_1^m,\cdots ,u_{N-1}^m\right)}^{\text{T}}$。

由分片线性插值基函数的性质知，(5.4)中的质量矩阵和刚度矩阵都是稀疏矩阵。

6. 数值案例

在这一节，我们将在MATLAB 2015a平台上进行编程计算，令 $u_{Mh}\left(x,y,z\right)$ 为精确解 $u\left(x,y,z\right)$ 的逼近解为， $r=Rt$，则有

$u\left(x,y,z\right)=\tilde{u}\left(t,\theta ,\varphi \right)={\displaystyle \underset{\left|m\right|=0}{\overset{\infty }{\sum }}{\displaystyle \underset{\left|l\right|=0}{\overset{m}{\sum }}{u}_m^l\left(t\right)Y_m^l}}$， $u_{Mh}\left(x,y,z\right)={\tilde{u}}_h\left(t,\theta ,\varphi \right)={\displaystyle \underset{\left|m\right|=0}{\overset{M}{\sum }}{\displaystyle \underset{\left|l\right|=0}{\overset{m}{\sum }}{u}_{mh}^l\left(t\right)Y_m^l}}$。

定义精确解和数值解的误差如下：

$e\left(u_{Mh}\left(x,y,z\right),u\left(x,y,z\right)\right)={\Vert u_{Mh}\left(x,y,z\right)-u\left(x,y,z\right)\Vert }_{L^{\infty }\left(\Omega \right)}={\Vert {\tilde{u}}_{Mh}\left(t,\theta ,\varphi \right)-\tilde{u}\left(t,\theta ,\varphi \right)\Vert }_{L^{\infty }\left(\mathcal{D}\right)}$.

例 取 $\alpha =R=1$ 且 $u={\left(x^2+y^2+z^2-1\right)}^2{\text{e}}^{x^2+y^2+z^2}$，显然u满足边值条件，将u代入(2.1)便可得到f。利用第5节中提出的算法，对于不同的M和N，我们在表1中给出了数值解与精确解的之间的误差 $e\left(u_{Mh}\left(x,y,z\right),u\left(x,y,z\right)\right)$。另外，为了更直观地表明算法的有效性，我们还在图1中分别给出数值解与精确解的图像，最后，为了验证该算法的有效性，我们呈现出了近似解的误差图在图2。

从表1可看出当 $N\ge 20,M=6$ 时，误差 $e\left(u_{Mh}\left(x,y,z\right),u\left(x,y,z\right)\right)$ 达到10⁻⁶左右的精度。同时，从图1和图2可看出我们算法是收敛的。

Table 1. The error e ( u M h ( x , y , z ) , u ( x , y , z ) ) between numerical solution and exact solution

表1. 数值解与精确解的误差 $e\left(u_{Mh}\left(x,y,z\right),u\left(x,y,z\right)\right)$

Figure 1. When $N=\text{20},m=12$, the figures of the exact solution (left) and the numerical solution (right) are shown below

图1. 当 $N=\text{20},m=12$ 时，精确解(左)和数值解(右)的图像分别如下所示

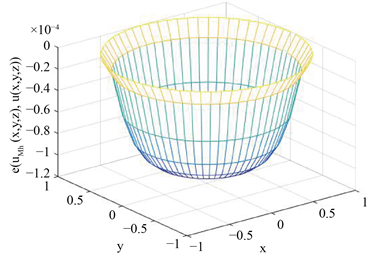
Figure 2. The error figures between exact solution and numerical solution with $N=10,m=6$ (left) and $N=25,m=10$ (right), respectively

图2. 当 $N=10,m=6$ (左)和 $N=25,m=10$ (右)时，精确解和数值解的误差图

7. 总结

本文提出了一种有效的有限元法求解球域上的二阶问题，亮点在于通过引入球坐标变化和球谐函数展开，将问题转化为一系列等价的一维问题，从而克服有限元在球域上剖分的困难，使得原问题更加容易解决。同时，并对这一系列一维问题进行了相应的误差分析。最后，我们提出的算法可应用到球域上更复杂的问题。