1. 引言
受群作用和环的模理论研究的启发,在众多的学科中都产生了半群作用相关结构。因此在不同的领域半群作用有着不同的名称,比如:S-自动机,S-操作数,S-多边形,S-集,S-代数等 [1] [2] [3] [4]。作为半群作用与偏序集理论的结合,S-poset理论近年来得到了发展 [5] - [10]。粗略地说,S-poset是一个带有序半群S-作用并且满足一定的相容条件的偏序集。
内射性是重要的范畴性质,在以S-poset为对象的范畴中,内射性也得到了众多的关注与研究 [1] [5] [6] [7] [11]。目前对于该范畴的研究,S通常被假定为一个序幺半群,带有的态射不同,该范畴的性质相应的也不同。为了得到以S-poset为对象的范畴中的内射对象的完整刻画,在文献 [11] 中,研究了以S-poset为对象以S-次可乘映射为态射构成的范畴中的内射对象,并进一步得到了S-poset相对于一类
态射的内射包。但,文献 [11] 中的主要结果是基于S为序幺半群得到的,因此,一个自然的问题是,这些结果能否推广到S是一般的序半群上,这是本文的主要动机。在以S-poset为对象以S-次可乘映射为态射构成的范畴中,对于一类特殊的态射
,本文构造了任意S-poset的内射包。
2. 预备知识
设P是一个偏序集 [12],
,定义
。如果
,则称A为下集。
。本文用到的其它有关偏序集的概念和结论请参考文献 [12]。
定义2.1 [13] 设
是半群,
是偏序集。如果
关于半群的乘法
是相容的,即
,有
,则称
为序半群。进一步,如果
是一个幺半群,则称
是序幺半群。
如果没有特别说明,本文中的
均为序半群,
表示一个序幺半群带有幺元1。
定义2.2 [5] 设
是一个偏序集,
是一个映射(
,
记为
)。如果对任意的
,满足以下条件:
(1)
;
(2)
,
则称
为S-poset,为方便简记为
或A。如果
是一个序幺半群,S1-poset A还需满足:
。
定义2.3 [11] 设
是S-poset,
是完备格,且
,都有
,则称
是一个S-quantale。
有伴右随,记为
。
设
和
是S-poset,称映射
是S-可乘的(相应的,S-次可乘的),如果
,
(相应的,
)。
设
和
是S-poset,称映射
是S-poset同态(相应的S-poset次同态),如果
是保序映射且f是S-可乘的(相应的,S-次可乘的)。
以S-poset为对象以S-poset同态为态射的范畴记为
。
以S-poset为对象以S-poset次同态为态射的范畴记为
。
定义2.4 [14] 设
是一个范畴,M是
中的一个态射类,
1) 称
中的对象C为M-内射的,如果对M中的任意态射
以及
中的态射
,都存在唯一的态射
使得
。
2) 称M中的态射
为M-本质的,如果对
中任意态射
,
有
。
3) 对于
中的对象A的和对象B,称对象B是对象A的M-内射包,如果对象B是M-内射的,且存在一个M-本质态射
。
有关范畴的相关知识,本文未作解释的请参考文献 [14]。
3. 主要结果
注意本文中的S是一个序半群而不是序幺半群。但是根据文献 [11],我们可以得到一系列相似的结论。为简明起见,我们省掉类似的证明。
设
表示是序嵌入的S-poset同态构成的类。设
表示范畴
中满足条件:
,
的态射构成的类。显然,
。
通过类似于文献 [11] 中命题4和命题5的证明,可以得到以下结论:
命题3.1 (1)设
是一个S-quantale,则
在范畴
中是
-内射的。
(2) 在范畴
中,每个S-quantale的收缩是S-quantale。
对任意一个偏序集P,
表示P的所有下集组成的集合。设
是一个S-poset。对任意的
,定义
.
.
可以证明
也是一个S-quantale。因此,由命题3.1我们可以知道
在范畴
中是
-内射的。而且,类似于文 [11] 中定理7的证明,可知
在范畴
中是
-内射的当且仅当
是一个S-quantale。
回忆一下偏序集P上的映射
被称为P上的闭包算子,如果j是保序的,增值的,幂等的。令
,即
。如果j是P上的闭包算子,则
,
。有关闭包算子的更多性质,请参考文献 [12]。
设
是S-poset,如果j是
上的闭包算子,且j是S-次可乘的,则j被称为
上的核映射。容易得到如下的结论:
1) 设j是S-poset
上的核映射,则
,
。
2) 设j是S-quantale
上的核映射,则
是S-quantale,其中,
,
。
设
是S-poset,对任意的
,定义
;
;
.
引理3.2设
是S-poset,则
是S-quantale
上的核映射,且
,
。
证明:容易验证
和
是
上的闭包算子。所以
是
上的闭包算子。设
,为证明
,只需证明
。
(1) 设
,则
。因为
,所以
,从而
,因此
。
(2) 设
,则
。所以
。从而
。
由(1) (2)可知
。
(3) 设
,则
。设
,则
,即
,所以
,从而
。因此
。
由引理3.2,可以得到如下的命题:
命题3.3设
是S-poset,则
是一个S-quantale。因此
在范畴
中是
内射的。
设
是S-poset,定义一个映射
为:
.
定理3.4设
是S-poset,则
是
在范畴
中的
-内射包。
证明:只需证明
是
-本质的。
(1) 设
,则
。所以
是S-次可乘的。又因为
是序嵌入,从而,
,因此
。
(2) 设
是S-poset次同态,且
。要证明
,只需证明
,
。
设
,
,则
,
。
(i) 设
,则
。对任意的
,有
因为
,从而
。由d的任意性可知
,所以
。对任意的
,有
,从而
,所以 。由于x的任意性,因此,
。由于x的任意性,因此,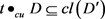 。
。
(ii) 设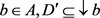 ,对任意的
,对任意的 ,有
,有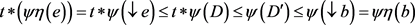 。由假设
。由假设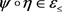 ,可得
,可得 。因此
。因此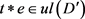 。
。
由于e的任意性,从而 ,所以
,所以 。因此
。因此 。
。
由(i)~(ii)可得 。
。
引理3.5在S1-poset 中,
中, 。
。
证明:设 ,设
,设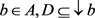 ,则
,则 。从而
。从而 ,所以
,所以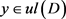 。所以
。所以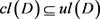 。因此
。因此 。
。
通过定理3.4,引理3.5,可以重新得到文献 [11] 的主要结论。
命题3.6设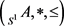 是S1-poset,则
是S1-poset,则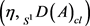 是
是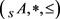 在范畴
在范畴 中的
中的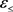 内射包。
内射包。
定义3.7设 是S-poset,如果对任意的
是S-poset,如果对任意的 ,
,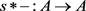 有右伴随,即有一个映射
有右伴随,即有一个映射 ,使得对任意的
,使得对任意的 ,
, ,则称S-poset
,则称S-poset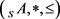 为剩余S-poset。
为剩余S-poset。
引理3.8在剩余S-poset 中,
中, 。
。
证明:设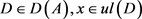 。设
。设 。则
。则 。
。 ,
, ,即
,即 ,从而,
,从而,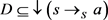 。由假设
。由假设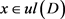 ,可得
,可得 ,即
,即 ,从而
,从而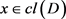 ,所以
,所以 ,因此
,因此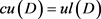 。
。
由定理3.4和引理3.8,我们可以得到如下的结论。
命题3.9设 是一个剩余S-poset,则
是一个剩余S-poset,则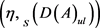 是
是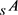 在范畴
在范畴 中的
中的 -内射包。
-内射包。
推论3.10在剩余S1-poset 中,
中, 。
。
4. 结论
本文运用序代数理论的相关知识,构造出了S-poset的内射包。并推广到S是序幺半群时的相应结果,最后得到剩余S-poset的内射包。