1. 引言
Allen-Cahn方程最初是作为研究结晶固体反相位边界运动的模型而被提出的 [1],该方程及其变形在图像处理 [2]、平均曲率运动 [3]、晶体的生长 [4]、和材料科学等实际问题中都发挥着极为重要的作用。
由于此类相场模型没有真解,因此选取有效的数值方法进行模拟尤为重要。Allen-Cahn方程的数值逼近方法有多种,包括半解析傅里叶谱法 [5],谱方法 [6],间断有限元方法 [7],算子分裂方法 [8] 以及求解高维Allen-Cahn方程的紧致差分交替方向隐式方法 [9] 等。近年来,也有学者采用自适应有限元方法 [10],无网格方法 [11] 对Allen-Cahn方程进行数值求解,上述工作均在直角坐标系下完成。但是,在许多实际问题中,需要考虑圆形区域,这方面的研究工作还不是很多 [12]。本文考虑在圆盘区域上求解Allen-Cahn方程,首先将拉普拉斯算子表示为极坐标中的形式,沿r方向和
方向进行网格剖分,然后采用中心差分方法在网格点上对Allen-Cahn方程进行空间离散,并将网格点上的数值解以矩阵形式表示。接下来发展积分因子方法进行时间离散,在时间离散过程中,利用梯形求积公式进行近似,使其精度为二阶精度。在实现过程中求解指数矩阵与向量的乘积时,采用Krylov子空间的方法来近似,而不单独求解指数矩阵。
2. 数值方法
考虑计算区域为
的二维非线性Allen-Cahn方程:
(1)
其中,
为扩散系数;
为拉普拉斯算子;
;
是一个给定的正参数且
,
设该方程在r方向边界条件为齐次Neumann边界,在
方向的边界条件为周期边界:
(2)
下面将方程(1)写成极坐标系下的形式:
(3)
将计算区域
分别沿r和
方向划分成
个网格,网格节点表示为
。在r方向的网格步长为
,在
方向的网
格步长为
。时间方向剖分为
。其中
为时间步长。设u在网格节点
处的数值解为
,结合泰勒展开式,在在网格点处对(3)式中的项进行离散,略去余项后,得到(3)式的二阶中心差分格式:
(4)
下面对边界上的差分格式进行修正使其达到二阶局部截断误差。考虑到方程(1)在r方向具有齐次
Neumann边界条件,当
时
,且
,当
时,
,将(4)式在r方向边
界的差分格式写为
(5)
考虑到u在
方向是以
为周期的,因此边界值为
,进而将(4)式在
方向边界的差分格式写为
(6)
定义离散解
为
阶的矩阵U,将非线性项记为F。将矩阵U和矩阵F按列重新排列成向量的形式,记
,
,结合(5)式与(6)式,定义矩阵A为
(7)
其中矩阵
。
矩阵
,
。
由上述矩阵的定义,将(1)式经过空间离散后,得到一组非线性常微分方程组:
(8)
下面采用积分因子方法求解方程(8)。两边同乘积分因子
,然后在一个时间步长内做积分得到:
(9)
对(9)式应用梯形积分公式近似得到:
(10)
令上式中的
,则(11)式可写为
(11)
虽然A为大型稀疏矩阵,而
为稠密矩阵,因此直接求解指数矩阵困难较大,本文利用Krylov子空间 [13]
的元素来近似指数矩阵与向量的乘积,即
,而不是单独求解指数矩阵。采用不动点迭代法在每个单元上求解非线性方程组(11),其中迭代初值选取为
。
3. 数值实验
应用本文提出的有限差分法和积分因子法求解下面的数值算例。考虑二维计算区域
,针对具有
方向具有齐次Neumann边界,
方向具有周期边界条件的方程(1)进行求解。初值选取形状像哑铃的函数,见图1(a)。
选取参数
,并在每个空间方向上取128个等分点,时间步长
。选取
这3个时间点,其数值结果如图1所示。
 (a)
(a)  (b)
(b) 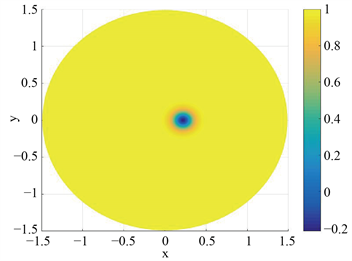 (c)
(c)  (d)
(d)
Figure 1. Numerical solution of the case
图1. 算例在
时的数值解
上图显示了在不同时间点上Allen-Cahn方程解的数值结果。结果表明,随着时间增大,其形状由初始时间
的哑铃状不断向圆形聚拢,最终消失。数值结果与文献 [7] 中的结果吻合。
基金项目
辽宁省自然科学基金(20180550996)资助的课题。