一类3D分片非线性系统的异宿环

Heterocilinic Cycle of a Class of 3D Piecewise Nonlinear Systems

摘要: 本文研究了一类具有两个鞍–焦点和一个不连续边界的3D分片非线性系统。通过恰当的变换确定了子系统的稳定流形和不稳定流形。基于稳定流形和不稳定流形建立了系统存在横截穿过切换面两次的异宿环的充分条件，并运用了一个数值实例验证结果的正确性。

Abstract: In this paper, one studies a class of 3D piecewise nonlinear systems with two saddle foci and one discontinuous boundary. The stable manifold and unstable manifold of the subsystem are deter-mined by coordinate transformation. Based on stable manifolds and unstable manifolds, the suffi-cient conditions for the existence of heteroclinic loops which cross the switching surface twice are given. Finally, a numerical example is given to verify the correctness of the theorem.

1. 引言

3D光滑混沌系统由于在保密通讯、图像加密等领域有广泛的应用前景，因而具有重要研究价值 [1] [2] [3]。但是如何严格证明任意3D光滑系统的混沌性是非常困难的。对于一类具有连接鞍–焦点的同宿轨或异宿环的3D光滑系统，Shil’nikov证明了其同宿轨或异宿环附近存在着混沌不变集 [4]，因此，连接鞍–焦点的同宿轨或异宿环对3D光滑系统的混沌性研究具有关键作用。然而如何证明任意3D光滑系统奇异环的存在性仍然是一个难题。尽管“钓鱼法”、Lyapunov函数法及定性方法是一些有效的方法去确定3D系统奇异环的存在性，但是这些方法只适用于某些特殊系统 [5] [6] [7]。

近几年，3D或4D分片线性系统奇异环与混沌不变集的存在性成为研究热点 [8] - [13]。2016年Wu证明了3D两片线性系统存在连接鞍–焦点同宿轨 [10]；2018年Yang等给出了4D两片线性系统存在只横截穿过切换面两次的同宿轨的充分条件 [11]；2018年Wu等证明了4D两片线性系统存在连接双焦点的异宿环 [12]；2019年Lu等给出了3D三片线性系统同宿轨与异宿环共存的充分条件 [13]。

相较于3D分片线性系统，对于3D分片非线性系统奇异环的存在性的研究较少。由于大多数的3D非线性系统是不可求解的，因此确定3D非线性系统的稳定流形和不稳定流形是非常不容易的。然而子系统的稳定流形和不稳定流形在构造分片系统奇异环的过程中发挥重要的作用，因而如何构造存在奇异环的3D分片非线性系统仍然是一个具有挑战性的工作。

本文讨论了一类具有两个鞍–焦点的3D两片非线性系统。通过恰当的变换确定了子系统的稳定流形和不稳定流形。基于构造3D分片线性系统异宿环的思想，严格证明了3D两片非线性系统存在连接鞍–焦点且只横截穿过切换面两次的异宿环，并运用一个数值实例验证结果的正确性。

2. 3D分片非线性系统

考虑如下3D分片非线性系统

$\stackrel{\dot{}}{X}=\{\begin{array}{l}{A}_{1}X+B_1,N^{\text{T}}X\le d,\\ A_2\left(X-P\right)+B_2,N^{\text{T}}X>d,\end{array}$ (1)

其中 $X={\left(x,y,z\right)}^{\text{T}}$， $P={\left(a,b,c\right)}^{\text{T}}$， $N^{\text{T}}=\left(n_1,n_2,n_3\right)$

$A_1=\left(\begin{array}{ccc}{\alpha }_1& {\beta }_1& 0\\ -{\beta }_1& {\alpha }_1& 0\\ 0& 0& -{\gamma }_1\end{array}\right),B_1=\left(\begin{array}{c}0\\ 0\\ e_1\left(x^2+y^2\right)\end{array}\right),$

$A_2=\left(\begin{array}{ccc}{\alpha }_2& {\beta }_2& 0\\ -{\beta }_2& {\alpha }_2& 0\\ 0& 0& -{\gamma }_2\end{array}\right),B_2=\left(\begin{array}{c}0\\ 0\\ e_2\left({\left(x-a\right)}^2+{\left(y-b\right)}^2\right)\end{array}\right).$

这里 ${\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2,e_1,e_2,n_3$ 均为正数，且 $0<d<a{n}_1+b{n}_2+c{n}_3$。

由于 $0<d<a{n}_1+b{n}_2+c{n}_3$，故系统(1)有两个鞍–焦点类型的平衡点 $O={\left(0,0,0\right)}^{\text{T}}$ 和 $P={\left(a,b,c\right)}^{\text{T}}$。

考虑系统(1)的两个子系统

$\stackrel{\dot{}}{X}=A_{1}X+B_1,$ (2)

$\stackrel{\dot{}}{X}=A_2\left(X-P\right)+B_2\text{.}$ (3)

显然系统(2)和(3)的稳定流形分别为

$W_{\left(2\right)}^s=\left\{{\left(0,0,z\right)}^{\text{T}}|z\in R\right\},W_{\left(3\right)}^s=\left\{{\left(a,b,z\right)}^{\text{T}}|z\in R\right\}.$

由条件 $n_3>0$ 得，在切换面 $N^{\text{T}}X=d$ 上存在一点 $Q_1$ 使得 $Q_1\in W_{\left(2\right)}^s$。通过计算可得

$Q_1={\left(0,0,\frac{d}{n_3}\right)}^{\text{T}};$

进一步在切换面 $N^{\text{T}}X=d$ 上也存在一点 $Q_2$ 满足 $Q_2\in W_{\left(3\right)}^s$。易知

$Q_2={\left(a,b,\frac{d-n_{1}a-n_{2}b}{n_3}\right)}^{\text{T}}.$

对系统(2)进行如下变换

$\{\begin{array}{l}u=x\\ v=y\\ w=z-k_1\left(x^2+y^2\right),\end{array}$

其中

$k_1=\frac{e_1}{2{\alpha }_1+{\gamma }_1}>0,$

则非线性系统(2)可化为下列系统

$\{\begin{array}{l}\stackrel{\dot{}}{u}={\alpha }_{1}u+{\beta }_{1}v\\ \stackrel{\dot{}}{v}=-{\beta }_{1}u+{\alpha }_{1}v\\ \stackrel{\dot{}}{w}=-{\gamma }_{1}w,\end{array}$

该系统为线性系统且平面 $w=0$ 为其不稳定平面。因此 $z=k_1\left(x^2+y^2\right)$ 为系统(2)的不稳定曲面。故系统(2)的不稳定流形为一个开口向上的抛物面

$W_{\left(2\right)}^u=\left\{{\left(x,y,k_1\left(x^2+y^2\right)\right)}^{\text{T}}|x,y\in R\right\}.$

由于系统(2)满足

$\{\begin{array}{l}\stackrel{\dot{}}{x}={\alpha }_{1}x+{\beta }_{1}y\\ \stackrel{\dot{}}{y}={\alpha }_{1}y-{\beta }_{1}x\end{array}$

故此线性微分方程组满足初始值 ${\left(x\left(0\right),y\left(0\right)\right)}^{\text{T}}={\left(x_0,y_0\right)}^{\text{T}}$ 的解为

$\{\begin{array}{l}x={\text{e}}^{{\alpha }_{1}t}\left(x_0\cos \left({\beta }_{1}t\right)+y_0\sin \left({\beta }_{1}t\right)\right)\\ y={\text{e}}^{{\alpha }_{1}t}\left(y_0\cos \left({\beta }_{1}t\right)-x_0\sin \left({\beta }_{1}t\right)\right),\end{array}$ (4)

因此系统(2)以 ${\left(x\left(0\right),y\left(0\right),z\left(0\right)\right)}^{\text{T}}={\left(x_0,y_0,k_1\left(x_0^2+y_0^2\right)\right)}^{\text{T}}$ 为初始值的解为

$\{\begin{array}{l}x={\text{e}}^{{\alpha }_{1}t}\left(x_0\cos \left({\beta }_{1}t\right)+y_0\sin \left({\beta }_{1}t\right)\right)\\ y={\text{e}}^{{\alpha }_{1}t}\left(y_0\cos \left({\beta }_{1}t\right)-x_0\sin \left({\beta }_{1}t\right)\right)\\ z=k_1\left(x_0^2+y_0^2\right){\text{e}}^{2{\alpha }_{1}t}.\end{array}$ (5)

同理，系统(3)的不稳定流形也为一个开口向上的抛物面

$W_{\left(3\right)}^u=\left\{{\left(x,y,k_2\left({\left(x-a\right)}^2+{\left(y-b\right)}^2\right)+c\right)}^{\text{T}}|x,y\in R\right\}.$

其中 $k_2=\frac{e_2}{2{\alpha }_2+{\gamma }_2}$。同时系统(3)以 ${\left(x\left(0\right),y\left(0\right),z\left(0\right)\right)}^{\text{T}}={\left(x_0,y_0,k_2\left({\left(x_0-a\right)}^2+{\left(y_0-b\right)}^2\right)+c\right)}^{\text{T}}$ 为初始值的解为

$\{\begin{array}{l}x={\text{e}}^{{\alpha }_{2}t}\left(\left(x_0-a\right)\cos \left({\beta }_{2}t\right)+\left(y_0-b\right)\sin \left({\beta }_{2}t\right)\right)+a\\ y={\text{e}}^{{\alpha }_{2}t}\left(-\left(x_0-a\right)\sin \left({\beta }_{2}t\right)+\left(y_0-b\right)\cos \left({\beta }_{2}t\right)\right)+b\\ z=k_2\left({\left(x_0-a\right)}^2+{\left(y_0-b\right)}^2\right){\text{e}}^{2{\alpha }_{2}t}+c.\end{array}$ (6)

3. 异宿环的存在性

本节证明3D分片非线性系统(1)的异宿环的存在性。

定理1若下列条件成立

1) $k_1{n}_3\left(a^2+b^2\right)=d-n_{1}a-n_{2}b,k_2{n}_3\left(a^2+b^2\right)=d-c{n}_3$。

2) ${\text{e}}^{-{\alpha }_1{t}_1}\frac{U_2{U}_4+U_1{U}_3}{\sqrt{U_3^2+U_4^2}}<d-n_3{k}_1\left(a^2+b^2\right){\text{e}}^{-2{\alpha }_1{t}_1},{\beta }_1{U}_2-{\alpha }_1{U}_1<0$。

3) $2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right)<{\alpha }_2{V}_2+{\beta }_2{V}_1<{\beta }_2\sqrt{V_1^2+V_2^2}<{\text{e}}^{{\alpha }_2{\tilde{t}}_2}\sqrt{{\alpha }_2^2+{\beta }_2^2}\left(S-d\right)$。

其中

$k_1=\frac{e_1}{2{\alpha }_1+{\gamma }_1},k_2=\frac{e_2}{2{\alpha }_2+{\gamma }_2}.$

$U_1=n_{1}a+n_{2}b,U_2=n_{2}a-n_{1}b,U_3={\alpha }_1{U}_2+{\beta }_1{U}_1,U_4={\beta }_1{U}_2-{\alpha }_1{U}_1\text{.}$

$t_1=\frac{1}{{\beta }_1}\arcsin \left(-\frac{U_4}{\sqrt{U_3^2+U_4^2}}\right)+\frac{2\pi }{{\beta }_1},{\tilde{t}}_2=\frac{2\pi }{{\beta }_2}-\frac{1}{{\beta }_2}\arcsin \left(\frac{{\alpha }_2{V}_2+{\beta }_2{V}_1}{\sqrt{{\alpha }_2^2+{\beta }_2^2}\sqrt{V_1^2+V_2^2}}\right).$

$V_1=n_{1}b-n_{2}a,V_2=n_{1}a+n_{2}b,S=n_{1}a+n_{2}b+n_{3}c.$

则系统(1)存在异宿环 ，且异宿环 仅横截穿过切换面 $N^{\text{T}}X=d$ 两次并经过

$Q_1={\left(0,0,\frac{d}{n_3}\right)}^{\text{T}},Q_2={\left(a,b,\frac{d-n_{1}a-n_{2}b}{n_3}\right)}^{\text{T}}.$

证明：设 $\phi \left(t,X_0\right)$ 表示系统(1)过初始值 $X_0$ 的轨线。要证明定理结论，只需证明下列条件成立

(i) $Q_1\in W_{\left(3\right)}^u,Q_2\in W_{\left(2\right)}^u$。

(ii) $\phi \left(t,Q_1\right)\to O,\phi \left(t,Q_2\right)\to P$，当 $t\to +\infty$。 $\phi \left(t,Q_1\right)\to P,\phi \left(t,Q_2\right)\to O$，当 $t\to -\infty$。

(iii) $N^{\text{T}}\left(A_1{Q}_1+B_1\right)N^{\text{T}}\left(A_2\left(Q_1-P\right)+B_2\right)>0$， $N^{\text{T}}\left(A_1{Q}_2+B_1\right)N^{\text{T}}\left(A_2\left(Q_2-P\right)+B_2\right)>0$。

首先证明条件(i)是成立的。由条件1)有

$Q_1={\left(0,0,\frac{d}{n_3}\right)}^{\text{T}}={\left(0,0,k_2\left(a^2+b^2\right)+c\right)}^{\text{T}}\in W_{\left(3\right)}^u,$

$Q_2={\left(a,b,\frac{d-n_{1}a-n_{2}b}{n_3}\right)}^{\text{T}}={\left(a,b,k_1\left(a^2+b^2\right)\right)}^{\text{T}}\in W_{\left(2\right)}^u.$

因此，条件(i)成立。

下面证明条件(ii)是成立的。由于 $Q_1\in W_{\left(2\right)}^s$， $Q_2\in W_{\left(3\right)}^s$ 且 $W_{\left(2\right)}^s$ 与 $W_{\left(3\right)}^s$ 均为直线，故当 $t\to +\infty$ 有

$\phi \left(t,Q_1\right)\to O,\phi \left(t,Q_2\right)\to P.$

注意到 $Q_2\in W_{\left(2\right)}^u$，因此若当 $t<0$ 时， $N^{\text{T}}\phi \left(t,Q_2\right)<d$ 恒成立，则有 $\phi \left(t,Q_2\right)\to O$，当 $t\to -\infty$。由(5)可得，当 $t<0$ 有

$\phi \left(t,Q_2\right)=\left(\begin{array}{c}{\text{e}}^{{\alpha }_{1}t}\left(a\cos \left({\beta }_{1}t\right)+b\sin \left({\beta }_{1}t\right)\right)\\ {\text{e}}^{{\alpha }_{1}t}\left(b\cos \left({\beta }_{1}t\right)-a\sin \left({\beta }_{1}t\right)\right)\\ k_1\left(a^2+b^2\right){\text{e}}^{2{\alpha }_{1}t}\end{array}\right).$

故

$N^{\text{T}}\phi \left(t,Q_2\right)={\text{e}}^{{\alpha }_{1}t}\left(\left(n_{1}a+n_{2}b\right)\cos \left({\beta }_{1}t\right)-\left(n_{2}a-n_{1}b\right)\sin \left({\beta }_{1}t\right)\right)+n_3{k}_1\left(a^2+b^2\right){\text{e}}^{2{\alpha }_{1}t}.$

记

$U_1=n_{1}a+n_{2}b,U_2=n_{2}a-n_{1}b,$

$f\left(t\right)={\text{e}}^{-{\alpha }_{1}t}\left(U_1\cos \left({\beta }_{1}t\right)+U_2\sin \left({\beta }_{1}t\right)\right),$

$h\left(t\right)=d-n_3{k}_1\left(a^2+b^2\right){\text{e}}^{-2{\alpha }_{1}t}.$

由于 $N^{\text{T}}\phi \left(t,Q_2\right)-d=f\left(-t\right)-h\left(-t\right)$，故只需证明当 $t>0$ 时， $f\left(t\right)<h\left(t\right)$ 恒成立。由于

$f^{\prime }\left(t\right)={\text{e}}^{-{\alpha }_{1}t}\left(U_4\cos \left({\beta }_{1}t\right)-U_3\sin \left({\beta }_{1}t\right)\right)\text{.}$

其中

$U_3={\alpha }_1{U}_2+{\beta }_1{U}_1,U_4={\beta }_1{U}_2-{\alpha }_1{U}_1.$

由 $f^{\prime }\left(t\right)=0$ 可得

$U_4\cos \left({\beta }_{1}t\right)-U_3\sin \left({\beta }_{1}t\right)=0.$

故函数 $f\left(t\right)$ 的驻点满足

$\sin \left({\beta }_{1}t\right)=\frac{U_4}{\sqrt{U_3^2+U_4^2}},\cos \left({\beta }_{1}t\right)=\frac{U_3}{\sqrt{U_3^2+U_4^2}}.$ (7)

或者

$\sin \left({\beta }_{1}t\right)=-\frac{U_4}{\sqrt{U_3^2+U_4^2}},\cos \left({\beta }_{1}t\right)=-\frac{U_3}{\sqrt{U_3^2+U_4^2}}.$ (8)

满足(7)且大于0的t可表示为

$t_i=\frac{1}{{\beta }_1}\arcsin \left(\frac{U_4}{\sqrt{U_3^2+U_4^2}}\right)+\frac{2i\pi }{{\beta }_1},i=1,2,3,\cdots$

满足(8)且大于0的t可表示为

${t^{\prime }}_j=-\frac{1}{{\beta }_1}\arcsin \left(\frac{U_4}{\sqrt{U_3^2+U_4^2}}\right)+\frac{2j\pi }{{\beta }_1},j=0,1,2,\cdots$

同时由于

$f^{″}\left(t\right)={\text{e}}^{-{\alpha }_{1}t}\left(\left({\alpha }_1{U}_3-{\beta }_1{U}_4\right)\sin \left({\beta }_{1}t\right)-\left({\alpha }_1{U}_4+{\beta }_1{U}_3\right)\cos \left({\beta }_{1}t\right)\right)\text{.}$

因此

$f^{″}\left(t_i\right)=-{\beta }_1{\text{e}}^{-{\alpha }_1{t}_i}\sqrt{U_3^2+U_4^2}<0.$

故 $t_i$ 是函数 $f\left(t\right)$ 的极大值点。同理可得

$f^{″}\left({t^{\prime }}_j\right)={\beta }_1{\text{e}}^{-{\alpha }_1{t^{\prime }}_j}\sqrt{U_3^2+U_4^2}>0.$

所以 ${t^{\prime }}_j$ 是函数 $f\left(t\right)$ 的极小值点，且函数 $f\left(t\right)$ 在 $t_i$ 的极大值满足

$f\left(t_i\right)={\text{e}}^{-{\alpha }_1{t}_i}\frac{U_2{U}_4+U_1{U}_3}{\sqrt{U_3^2+U_4^2}}\le {\text{e}}^{-{\alpha }_1{t}_1}\frac{U_2{U}_4+U_1{U}_3}{\sqrt{U_3^2+U_4^2}}=f\left(t_1\right).$

由于点 $Q_2$ 位于切换面上，故有 $N^{\text{T}}\phi \left(0,Q_2\right)=0$，即 $f\left(0\right)=h\left(0\right)$。由条件2)可得

$f^{\prime }\left(0\right)=U_4<0.$

同时注意到函数 $h\left(t\right)$ 是单调增加的。因此当 $t>0$ 时，函数 $f\left(t\right)$ 和 $h\left(t\right)$ 的图像如图1所示。

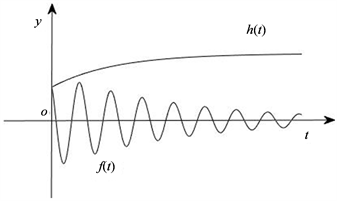
Figure 1. The image of $f\left(t\right)$ and $h(\; t\; )$

图1. 函数 $f\left(t\right)$ 和 $h\left(t\right)$ 的图像

若 $t_1$ 满足

$f\left(t_1\right)<h\left(t_1\right).$

那么有

$f\left(t\right)<h\left(t\right),t\in \left(0,+\infty \right)\text{.}$

同时由条件2)可得

$f\left(t_1\right)={\text{e}}^{-{\alpha }_1{t}_1}\frac{U_2{U}_4+U_1{U}_3}{\sqrt{U_3^2+U_4^2}}<d-n_3{k}_1\left(a^2+b^2\right){\text{e}}^{-2{\alpha }_1{t}_1}=h\left(t_1\right).$

所以当 $t<0$ 时， $N^{\text{T}}\phi \left(t,Q_2\right)<d$ 恒成立，有 $\phi \left(t,Q_2\right)\to O$，当 $t\to -\infty$。

由于 $Q_1\in W_{\left(3\right)}^u$，因此若当 $t<0$ 时， $N^{\text{T}}\phi \left(t,Q_1\right)>d$ 恒成立，则有 $\phi \left(t,Q_1\right)\to P$，当 $t\to -\infty$。由(6)可得，当 $t<0$ 有

$\phi \left(t,Q_1\right)=\left(\begin{array}{c}{\text{e}}^{{\alpha }_{2}t}\left(-b\sin \left({\beta }_{2}t\right)-a\cos \left({\beta }_{2}t\right)\right)+a\\ {\text{e}}^{{\alpha }_{2}t}\left(a\sin \left({\beta }_{2}t\right)-b\cos \left({\beta }_{2}t\right)\right)+b\\ k_2\left(a^2+b^2\right){\text{e}}^{2{\alpha }_2{t}_1}+c\end{array}\right).$

所以

$\begin{array}{l}{N}^{\text{T}}\phi \left(t,Q_1\right)={\text{e}}^{{\alpha }_{2}t}\left(\left(n_{2}a-n_{1}b\right)\sin \left({\beta }_{2}t\right)-\left(n_{2}b+n_{1}a\right)\cos \left({\beta }_{2}t\right)\right)\\ +n_3{k}_2\left(a^2+b^2\right){\text{e}}^{2{\alpha }_{2}t}+n_{1}a+n_{2}b+n_{3}c.\end{array}$

记

$V_1=n_{1}b-n_{2}a,V_2=n_{1}a+n_{2}b,$

$m\left(t\right)=d-n_{1}a-n_{2}b-n_{3}c-n_3{k}_2\left(a^2+b^2\right){\text{e}}^{-2{\alpha }_{2}t},$

$g\left(t\right)={\text{e}}^{-{\alpha }_{2}t}\left(V_1\sin \left({\beta }_{2}t\right)-V_2\cos \left({\beta }_{2}t\right)\right)={\text{e}}^{-{\alpha }_{2}t}\sqrt{V_1^2+V_2^2}\sin \left({\beta }_{2}t+{\theta }_1\right).$

其中 ${\theta }_1$ 满足

$\sin {\theta }_1=-\frac{V_2}{\sqrt{V_1^2+V_2^2}},\cos {\theta }_1=\frac{V_1}{\sqrt{V_1^2+V_2^2}}.$

由于 $N^{\text{T}}\phi \left(0,Q_1\right)=0$，故有

$-V_2=g\left(0\right)=m\left(0\right)=d-n_{1}a-n_{2}b-n_{3}c-n_3{k}_2\left(a^2+b^2\right)<0.$

因此有 ${\theta }_1\in \left(-\pi ,0\right)$。由于 $N^{\text{T}}\phi \left(t,Q_1\right)-d=g\left(-t\right)-m\left(-t\right)$，因此只需证明当 $t>0$ 时， $g\left(t\right)>m\left(t\right)$ 恒成立。

当 $t>0$ 时，函数 $g\left(t\right)$ 和 $m\left(t\right)$ 的图像如图2所示。

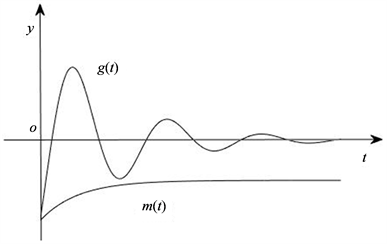
Figure 2. The image of $g\left(t\right)$ and $m(\; t\; )$

图2. 函数 $g\left(t\right)$ 和 $m\left(t\right)$ 的图像

记

$G\left(t\right)=g\left(t\right)-m\left(t\right).$

则有

$G^{\prime }\left(t\right)={\text{e}}^{-{\alpha }_{2}t}\sqrt{V_1^2+V_2^2}\sqrt{{\alpha }_2^2+{\beta }_2^2}\sin \left({\beta }_{2}t+{\theta }_1+{\theta }_2\right)-2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right){\text{e}}^{-2{\alpha }_{2}t}.$

其中 ${\theta }_2$ 满足

$\sin {\theta }_2=\frac{{\beta }_2}{\sqrt{{\alpha }_2^2+{\beta }_2^2}},\cos {\theta }_2=-\frac{{\alpha }_2}{\sqrt{{\alpha }_2^2+{\beta }_2^2}}.$

因此有 ${\theta }_2\in \left(\frac{\pi }{2},\pi \right)$。由条件3)可得

$\sin \left({\theta }_1+{\theta }_2\right)=\frac{{\alpha }_2{V}_2+{\beta }_2{V}_1}{\sqrt{{\alpha }_2^2+{\beta }_2^2}\sqrt{V_1^2+V_2^2}}>0.$

因此有 ${\theta }_1+{\theta }_2\in \left(0,\pi \right)$。由条件3)可知

$G^{\prime }\left(0\right)={\alpha }_2{V}_2+{\beta }_2{V}_1-2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right)>0.$

而当 $t\in \left(0,-\frac{{\theta }_1}{{\beta }_2}\right)$ 有 ${\beta }_{2}t+{\theta }_1+{\theta }_2\in \left({\theta }_1+{\theta }_2,{\theta }_2\right)$。由条件3)可得当 $t\in \left(0,-\frac{{\theta }_1}{{\beta }_2}\right)$

$\begin{array}{c}{G}^{\prime }\left(t\right)>{\text{e}}^{-{\alpha }_{2}t}\left(\sqrt{V_1^2+V_2^2}\sqrt{{\alpha }_2^2+{\beta }_2^2}\sin \left({\beta }_{2}t+{\theta }_1+{\theta }_2\right)-2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right)\right)\\ >{\text{e}}^{-{\alpha }_{2}t}\left(\sqrt{V_1^2+V_2^2}\sqrt{{\alpha }_2^2+{\beta }_2^2}\min \left\{\sin \left({\theta }_1+{\theta }_2\right),\sin \left({\theta }_2\right)\right\}-2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right)\right)\\ ={\text{e}}^{-{\alpha }_{2}t}\left(\sqrt{V_1^2+V_2^2}\sqrt{{\alpha }_2^2+{\beta }_2^2}\sin \left({\theta }_1+{\theta }_2\right)-2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right)\right)\\ ={\text{e}}^{-{\alpha }_{2}t}{G}^{\prime }\left(0\right)>0.\end{array}$

所以当 $t\in \left(0,-\frac{{\theta }_1}{{\beta }_2}\right)$，函数 $G\left(t\right)$ 是单调增加的。注意到 $G\left(0\right)=0$，所以对于 $t\in \left(0,-\frac{{\theta }_1}{{\beta }_2}\right)$ 有 $g\left(t\right)>m\left(t\right)$。

同时

$g\left(-\frac{{\theta }_1}{{\beta }_2}\right)=0,$

$m\left(-\frac{{\theta }_1}{{\beta }_2}\right)<d-n_{1}a-n_{2}b-n_{3}c<0.$

显然，对于 $t\in \left(-\frac{{\theta }_1}{{\beta }_2},+\infty \right)$ 有

$m\left(t\right)<d-n_{1}a-n_{2}b-n_{3}c.$

因此若

$g\left(t\right)\ge d-n_{1}a-n_{2}b-n_{3}c.$

那么就有当 $t>0$ 时， $g\left(t\right)>m\left(t\right)$ 成立。同时

$g^{\prime }\left(t\right)={\text{e}}^{-{\alpha }_{2}t}\sqrt{V_1^2+V_2^2}\sqrt{{\alpha }_2^2+{\beta }_2^2}\sin \left({\beta }_{2}t+{\theta }_1+{\theta }_2\right),$

$g^{″}\left(t\right)={\text{e}}^{-{\alpha }_{2}t}\sqrt{V_1^2+V_2^2}\left({\alpha }_2^2+{\beta }_2^2\right)\sin \left({\beta }_{2}t+{\theta }_1+2{\theta }_2\right)\text{.}$

因此函数 $g\left(t\right)$ 的驻点为

${\tilde{t}}_k=\frac{k\pi -{\theta }_1-{\theta }_2}{{\beta }_2},k=1,2,3,\cdots$

当k为偶数时

$g^{″}\left({\tilde{t}}_k\right)={\text{e}}^{-{\alpha }_2{\tilde{t}}_k}\sqrt{V_1^2+V_2^2}\left({\alpha }_2^2+{\beta }_2^2\right)\sin \left({\theta }_2\right)>0.$

当k为奇数时

$g^{″}\left({\tilde{t}}_k\right)=-{\text{e}}^{-{\alpha }_2{\tilde{t}}_k}\sqrt{V_1^2+V_2^2}\left({\alpha }_2^2+{\beta }_2^2\right)\sin \left({\theta }_2\right)<0.$

所以 ${\tilde{t}}_{2k}$ 是函数 $g\left(t\right)$ 的极小值点， ${\tilde{t}}_{2k-1}$ 是函数 $g\left(t\right)$ 的极大值点。同时注意到

$g\left({\tilde{t}}_{2k}\right)=-{\text{e}}^{-{\alpha }_2{\tilde{t}}_{2k}}\sqrt{V_1^2+V_2^2}\sin \left({\theta }_2\right)\ge -{\text{e}}^{-{\alpha }_2{\tilde{t}}_2}\sqrt{V_1^2+V_2^2}\sin \left({\theta }_2\right)=g\left({\tilde{t}}_2\right)\text{.}$

由条件3)可得

$-{\text{e}}^{-{\alpha }_2{\tilde{t}}_2}\sqrt{V_1^2+V_2^2}\sin \left({\theta }_2\right)=-{\text{e}}^{-{\alpha }_2{\tilde{t}}_2}\frac{{\beta }_2\sqrt{V_1^2+V_2^2}}{\sqrt{{\alpha }_2^2+{\beta }_2^2}}>d-n_{1}a-n_{2}b-n_{3}c\text{.}$

因此当 $t>0$ 时， $g\left(t\right)>m\left(t\right)$ 恒成立。故条件(ii)是成立的。

下面说明条件(iii)是成立的。由于

$N^{\text{T}}\left(A_1{Q}_1+B_1\right)=-{\gamma }_{1}d<0$

$N^{\text{T}}\left(A_2\left(Q_1-P\right)+B_2\right)=2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right)-{\alpha }_2{V}_2-{\beta }_2{V}_1<0$

$N^{\text{T}}\left(A_2\left(Q_2-P\right)+B_2\right)=-{\gamma }_2\left(d-n_{1}a-n_{2}b-n_{3}c\right)>0$

$N^{\text{T}}\left(A_1{Q}_2+B_1\right)={\alpha }_1{U}_1-{\beta }_1{U}_2+2{\alpha }_1{n}_3{k}_1\left(a^2+b^2\right)>0$

因此条件(iii)是成立。

因此系统(1)存在只横截穿过切换面两次的异宿环Г，且异宿环Г仅横截穿过切换面 $N^{\text{T}}X=d$ 两次并经过点 $Q_1$ 和 $Q_2$，故定理得证。

当系统(1)中的 $e_1=e_2=0$ 时，系统(1)就由3D分片非线性系统转化为3D分片线性系统。根据定理1可得如下推论。

推论1：若 $e_1=e_2=0$，则3D分片线性系统(1)存在横截穿过切换面 $N^{\text{T}}X=d$ 两次的异宿环的充分条件为

1) $d=n_{1}a+n_{2}b=c{n}_3$。

2) ${\text{e}}^{-{\alpha }_1{t}_1}\frac{U_2{U}_4+U_1{U}_3}{\sqrt{U_3^2+U_4^2}}<d,{\beta }_1{U}_2-{\alpha }_1{U}_1<0$。

3) $0<{\alpha }_2{V}_2+{\beta }_2{V}_1<{\beta }_2\sqrt{V_1^2+V_2^2}<{\text{e}}^{{\alpha }_2{\tilde{t}}_2}\sqrt{{\alpha }_2^2+{\beta }_2^2}d$。

其中

$U_1=n_{1}a+n_{2}b,U_2=n_{2}a-n_{1}b,U_3={\alpha }_1{U}_2+{\beta }_1{U}_1,U_4={\beta }_1{U}_2-{\alpha }_1{U}_1.$

$t_1=\frac{1}{{\beta }_1}\arcsin \left(-\frac{U_4}{\sqrt{U_3^2+U_4^2}}\right)+\frac{2\pi }{{\beta }_1},{\tilde{t}}_2=\frac{2\pi }{{\beta }_2}-\frac{1}{{\beta }_2}\arcsin \left(\frac{{\alpha }_2{V}_2+{\beta }_2{V}_1}{\sqrt{{\alpha }_2^2+{\beta }_2^2}\sqrt{V_1^2+V_2^2}}\right).$

$V_1=n_{1}b-n_{2}a,V_2=n_{1}a+n_{2}b.$

4. 数值实例

考虑取如下参数的非线性系统(1)

${\alpha }_1=0.2,{\beta }_1=4,e_1=8.8,{\gamma }_1=4,$

${\alpha }_2=0.9,{\beta }_2=4,e_2=5.8,{\gamma }_4=4,$

$a=0,b=0.5,c=0.75,$

$n_1=n_2=n_3=d=1.$

故可得

$Q_1={\left(0,0,\frac{d}{n_3}\right)}^{\text{T}}={\left(0,0,1\right)}^{\text{T}},Q_2={\left(a,b,\frac{d-n_{1}a-n_{2}b}{n_3}\right)}^{\text{T}}={\left(0,0.5,0.5\right)}^{\text{T}},$

$k_1=\frac{e_1}{2{\alpha }_1+r_1}=2,k_2=\frac{e_2}{2{\alpha }_2+{\gamma }_2}=1.$

由于

$k_1{n}_3\left(a^2+b^2\right)=d-n_{1}a-n_{2}b=0.5,$

$k_2{n}_3\left(a^2+b^2\right)=d-c{n}_3=0.25,$

$U_1=n_{1}a+n_{2}b=0.5,U_2=n_{2}a-n_{1}b=-0.5,$

$U_3={\alpha }_1{U}_2+{\beta }_1{U}_1=1.9,U_4={\beta }_1{U}_2-{\alpha }_1{U}_1=-2.1,$

$V_1=n_{1}b-n_{2}a=0.5,V_2=n_{2}b+n_{1}a=0.5,S=n_{1}a+n_{2}b+n_{3}c=1.25,$

$t_1=\frac{1}{{\beta }_1}\arcsin \left(-\frac{U_4}{\sqrt{U_3^2+U_4^2}}\right)+\frac{2\pi }{{\beta }_1}\approx 1.7796,$

${\tilde{t}}_2=\frac{2\pi }{{\beta }_2}-\frac{1}{{\beta }_2}\arcsin \left(\frac{{\alpha }_2{V}_2+{\beta }_2{V}_1}{\sqrt{{\alpha }_2^2+{\beta }_2^2}\sqrt{V_1^2+V_2^2}}\right)\approx 1.3191,$

${\text{e}}^{-{\alpha }_1{t}_1}\frac{U_2{U}_4+U_1{U}_3}{\sqrt{U_3^2+U_4^2}}\approx 0.4947<d-n_3{k}_1\left(a^2+b^2\right){\text{e}}^{-2{\alpha }_1{t}_1}\approx 0.7546,$

${\beta }_1{U}_2-{\alpha }_1{U}_1=-2.1<0,$

$2{\alpha }_2{n}_3{k}_2\left(a^2+b^2\right)=0.45<{\alpha }_2{V}_2+{\beta }_2{V}_1=2.45,$

${\beta }_2\sqrt{V_1^2+V_2^2}\approx 2.8284<{\text{e}}^{{\alpha }_2{\tilde{t}}_2}\sqrt{{\alpha }_2^2+{\beta }_2^2}\left(n_{1}a+n_{2}b+n_{3}c-d\right)\approx \mathrm{3.2779.}$

即定理1的条件满足，故由定理1可得系统(1)存在只横截穿过切换面两次的异宿环，如图3所示。

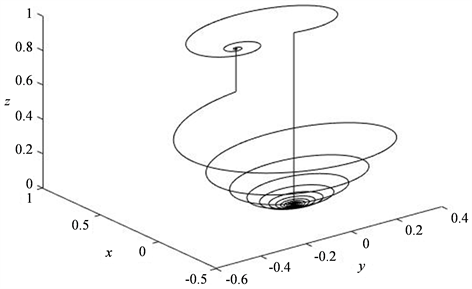
Figure 3. The heteroclinic cycle of system (1)

图3. 系统(1)的异宿环

5. 总结

本文发现了一类具有两个鞍–焦点的3D分片非线性系统。通过对此系统的子系统的分析，获得系统的稳定流形和不稳定流形。在系统的稳定流形、不稳定流形基础上建立了系统(1)存在只横截穿过切换面两次。特别地，当系统(1)中的参数 $e_1$ 和 $e_2$ 均为零时，系统(1)就转化为3D分片线性系统，从而得到一类3D分片线性系统的存在异宿环的判定条件。

基金项目

国家自然科学基金(12071151)。