1. 引言
PZT在极化后具有良好的压电性能,其压电系数大、居里温度高、各项机电参数受温度影响小、时间稳定性好、易于集成 [1] [2] [3],加上本身材质坚硬,不受外界恶劣环境影响等优点 [4] [5],常用于光纤相位调制器的制作,以实现信息在光纤中的传输 [6] [7]。
PZT压电陶瓷通过逆压电效应实现相位的调制 [8] [9]。逆压电效应是指在陶瓷管上施加一个与极化方向相同或者相反的电场,会使陶瓷管产生极化方向上的伸缩形变的现象 [10] [11] [12]。开环光纤电流传感器是PZT压电陶瓷作为相位调制器的典型应用。原理图如图1所示:
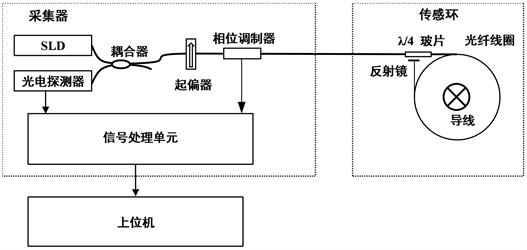
Figure 1. Principle diagram of FOCS
图1. 开环光纤电流传感器原理图
开环FOCS是基于法拉第效应和安培效应,以光纤作为传输和测量介质,PZT压电陶瓷作为相位调制器 [13],解调光纤中传输的一束正交偏振光的相位差得到电流信号的一种电流测量装置 [14] [15]。随着智能电网战略的推进深化和直流输电工程的快速建设,开环光纤电流传感器以其抗电磁干扰能力强、测量范围大,响应速度快、稳定性好、易于安装等优点,被越来越多地应用在电力自动控制,故障诊断、计量等领域 [16] [17] [18]。PZT相位调制器的调制性能是决定开环光纤电流传感器测量精度和稳定性的基本和关键因素之一 [19] [20]。
本文对用在开环光纤电流传感器中的PZT相位调制器的调制机理进行了阐述说明和理论分析,对影响PZT的调制性能的参数进行了分析研究,推导了在PZT相位调制器上加载的驱动电压与相位改变量之间的关系,并通过搭建开环光纤电流传感器试验样机从试验上对推导结果和代表PZT相位调制性能的参数——调制深度的温度稳定性进行了验证。
2. PZT相位调制机理
2.1. 加载电压与相位变化
PZT相位调制器通过在PZT上施加调制电压产生逆压电效应,使PZT发生伸缩形变,引起缠绕在PZT管上的光纤长度、纤芯直径和折射率的变化,使在光纤中传输的光波发生相位变化,进而实现相位调制的目的,其示意图如图2所示。
在PZT相位调制器的内壁和外壁间施加电压
时,PZT管上的周长变化量可表示为 [15] [16]:
(1)
式中
为压电应变系数(脚注中第一位数字表示PZT压电陶瓷的极化方向;第二位数字表示PZT压电陶瓷的机械振动方向),l和∆l分别为PZT压电陶瓷管的周长及其变化量,
分别为PZT管的外直径和内直径,
为谐振频率,
为调制频率,C为弹光系数。
假设保偏光纤中的固有双折射为∆n,光纤中传输的光波波长为
,长度为l的单匝光纤产生的轴向应变为
,相应的径向应变为
,光线的轴向应变
引起径向应变的
、
产生的应变双折射为
。应变模式双折射
产生的相位差:
(2)
由于掺杂区与包层的泊松系数差异,当光纤发生轴向应变时,会产生附加的双折射。由于泊松系数的差异,在横截面上产生非圆对称的应力分布,轴向应力产生的应力模式双折射
,则双折射
为:
(3)
其中C为弹光系数,E是杨氏模量,
是纤芯的应变系数随归一化半径r (光纤的外径为r = 1)和角度θ分布函数,其中ν是光纤材料的泊松比。由(2)式可知,对于应力型高双折射光纤发生轴向应变
时,应力模式双折射
产生的相位差为:
(4)
其中
为与光纤材料本身有关的比例系数。综上所述,当薄片光纤在轴向应力的作用下发生轴向应变
时,一段保偏光纤中的相位差
可表示为:
(5)
由于纤芯的直径变化引起的光波相位变化比其他两种应变所引起的相位变化小很多,可以忽略。
假设PZT管的径向变化与绕制的多匝光纤的轴向变化传递函数为1,则PZT管的周长变化量为每匝光纤长度的变化量,在压电陶瓷曲面绕制N匝保偏光纤,波长为
的光波通过光纤总长度为
的光纤相位调制器后,发生的相位变化可表示为:
(6)
式中,
为光纤总长度变化量。此外,在输入高频电压信号的情况下,折射率变化引起的相位变化远大于长度变化引起的相位变化,所以在实际应用中仅考虑折射率变化引起光波相位变化。设定PZT加载的调制电压频率大小与PZT管的谐振频率相同,综合式(1)、式(6)可得:
(7)
2.2. 相位变化与调制深度
假设PZT采用正弦电压进行调制,PZT在t时刻产生的相位为
(8)
式(8)中
为相位调制器在t时刻作用于光纤传感环产生的相位延迟,
为PZT相位调制器的调制系数,
为施加在相位调制器的调制电压,
为调制电压幅值,
为调制电压信号的频率。
光源光信号经调制后产生的输出光信号为
(9)
上式中k为光路中光信号传输时与器件连接时产生的线性叠加损耗的相关系数。
为Faraday磁光效应产生的相位偏移。τ为顺、逆时针相向传输光波在光纤环中先后的渡越时间。定义输出光信号中由相位调制器产生的不含时间变量的系数为调制深度为
,式(8)中的调制深度为
(10)
因此,光电探测器接收的光信号可改写为:
(11)
光电探测器将探测到的光信号转换为电信号输出,再经信号调理、模数转换后通过贝塞尔函数对电压信号进行谐波分析和算法解调得到调制深度。调制信号的幅值和PZT相位调制器调制的灵敏度与调制深度
有关,PZT的工作状态可以用调制深度
表示 [20] [21] [22]。
3. 试验和分析
通过对PZT相位调制器的理论分析可知,在理想状态下对于同一个PZT相位调制器,PZT相位调制器上施加的调制电压,会等比例的引起在光纤中传输的相位变化,PZT的调制性能优劣决定调制电压与相位变化之间的线性关系。
对于光纤电流传感器,温度变化对测量准确度的影响是衡量其性能的关键指标 [23]。为测试PZT相位调制的温度特性,在温箱中模拟外界环境变化,搭建了开环光纤电流传感器进行试验。
3.1. PZT的调制性能试验
为验证PZT的调制性能和温度稳定性,搭建了如图1所示的开环光纤电流传感器样机进行试验。在开环FOCS样机中,在PZT管内外壁之间施加正弦调制电压信号,设定PZT调制电压频率与其谐振频率大小相等为83.33 kHz,调节PZT加载电压幅值的大小,得到PZT调制电压与对应调制深度的关系如图3所示:
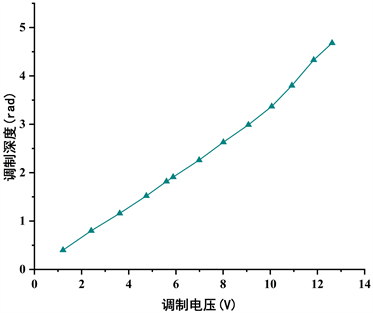
Figure 3. The relation curve of the voltage applied on the PZT and modulation depth
图3. PZT加载电压与调制深度的关系曲线
由图3,在0~10 V调制电压范围内PZT的调制深度与加载电压呈线性关系,表明了PZT在加载调制电压时具有良好的调制性能,施加合适的调制电压可实现对PZT相位调制器调制性能的精确控制。
3.2. PZT调制性能的温度特性试验
调节加载电压,使PZT相位调制器的调制深度为1.84,此时加载电压为5.6 V,保持加载电压不变,室温控制在24℃,进行PZT调制特性的稳定性试验,试验结果如图4所示,PZT的调制深度在常温下的误差为1.2%,表明了PZT在常温下良好的调制性能和稳定性。
为验证PZT相位调制器调制性能的温度稳定性,将试验样机中的PZT相位调制器放置在温箱中,设置温箱温度范围−40℃~+85℃,温变速率为1℃/3min,温度循环曲线和测得的PZT相位调制器温度与调制深度的关系曲线如图5所示。
由图5在温度变化过程中,调制深度随时间变化,但在恒温+85℃、−40℃和+25℃时,PZT相位调制器的调制深度大小基本保持不变,表明了PZT调制性能随温度变化的温度特性。同时在从低温(−40℃)回常温(+25℃),和高温(+85℃)回常温(+25℃)变温过程结束后,PZT的调制深度可以回到初始常温时的大小,因此可以通过对PZT调制深度进行温度补偿来保证FOCS的精度 [23] [24]。

Figure 4. The modulation characteristics of PZT at a room temperature
图4. PZT常温调制特性

Figure 5. The curve of the modulation depth of PZT, when FOCS is in a high-low temperature cycle
图5. PZT调制深度温度特性曲线
4. 结语
本文对开环FOCS的原理进行了概述,阐述了PZT相位调制器的调制原理,并对开环FOCS用到的PZT相位调制器的调制特性进行了理论分析,该模型可以准确分析出引起相位变化的原因,从由PZT管周长变化引起的光纤应变和应变模式下光纤长度变化量和折射率变化上分析,推导出了引起相位变化的主要是由光纤伸缩引起的光纤折射率变化引起的,得到了PZT相位调制器加载电压后由逆压电效应引起的相位变化与代表其调制性能的参数——调制深度的关系,并根据推导结果对PZT相位调制器调制性能进行了常温稳定性与全温稳定性验证测试,试验结果表明了PZT相位调制器调制性能的温度特性,并通过数据结果分析得到可以通过温度补偿来实现PZT相位调制器调制深度的温度稳定性的结论,这对PZT调制特性的精确控制、灵敏度的提升与PZT相位调制器的优化设计和工程化应用具有重要指导意义。
基金项目
国家重点研发计划项目2019YFC1509502。
NOTES
*通讯作者。