论“抓大头”在求极限中的应用

On the Application of “Grasping the Big Head” in Seeking the Limit

摘要: 高等数学中的一系列重要概念，如函数的连续性、导数以及定积分等都是借助于极限来定义的。正确掌握函数的极限运算方法和运算技巧，对学习好高等数学具有重要意义。本文定义“大头”的概念，给出“大头”的性质和定理，借助于“抓大头”思想解决微积分中一类极限，并通过讲解具有代表性的研究生入学考试真题、大学生数学竞赛题和广东省普通高校本科生招生考试真题，对方法运用加以阐明。

Abstract: A series of important concepts in higher mathematics, such as the continuity of function, derivative and definite integral, are defined by means of limit. It is of great significance to master the operation methods and skills of function limit for learning higher mathematics. In this paper, the concept of “big head” is defined, the properties and theorems of “big head” are given. With the help of “grasping the big head”, a kind of limit in calculus is solved. The application of the method is il-lustrated by explaining the representative real questions of postgraduate entrance examination, mathematical contest of college students and real problems of undergraduate production entrance examination in Guangdong Province.

1. 引言

极限是高等数学中一个十分重要的概念，高等数学中函数的连续性、导数以及定积分等都是借助于极限来定义的。可以说高等数学就是一门用极限思想来研究函数的学科。通过对历年全国硕士研究生入学考试的数学真题以及全国大学生数学竞赛真题研究分析发现，几乎每年都有一道求极限的题目，从中可见其重要性。在求极限中，通常会涉及几个函数的代数和的极限，而这些函数在自变量的变化过程中的地位也不同，如何抓住主要的、本质的进行计算是简化计算极限的关键，现有文献 [1] [2] [3] [4] 以及相关文献中都没有涉及这类知识。本文定义“大头”的概念，给出“大头”的性质和定理，借助于“抓大头”思想解决微积分中一类极限，并通过讲解具有代表性的研究生入学考试真题和大学生数学竞赛题等，对方法运用加以阐明。

2. “大头”的概念及性质

定义2.1若 $\underset{x\to \ast }{\lim }\frac{f_2\left(x\right)}{f_1\left(x\right)}=0$，则称 $f_1\left(x\right)$ 为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头，其中 $\ast$ 表示 $x_0$， $x_0^{+}$， $x_0^{-}$， $\infty$， $+\infty$， $-\infty$ 中的一种，下同。

性质1若 $f_1\left(x\right)$ 为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头，则 $k_1{f}_1\left(x\right)$ 为当 $x\to \ast$ 时 $k_1{f}_1\left(x\right)+k_2{f}_2\left(x\right)\left(k_1\ne 0\right)$ 中的大头。

证明：因为 $f_1\left(x\right)$ 为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头，即 $\underset{x\to \ast }{\lim }\frac{f_2\left(x\right)}{f_1\left(x\right)}=0$，于是

$\underset{x\to \ast }{\lim }\frac{k_2{f}_2\left(x\right)}{k_1{f}_1\left(x\right)}=\frac{k_2}{k_1}\underset{x\to \ast }{\lim }\frac{f_2\left(x\right)}{f_1\left(x\right)}=0$ ,

即 $k_1{f}_1\left(x\right)$ 为当 $x\to \ast$ 时 $k_1{f}_1\left(x\right)+k_2{f}_2\left(x\right)\left(k_1\ne 0\right)$ 中的大头。

性质2 若 $f_1\left(x\right)$ 和 $g_1\left(x\right)$ 分别为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头和 $g_1\left(x\right)+g_2\left(x\right)$ 中的大头，则 $f_1\left(x\right)g_1\left(x\right)$ 为当 $x\to \ast$ 时 $\left(f_1\left(x\right)+f_2\left(x\right)\right)\left(g_1\left(x\right)+g_2\left(x\right)\right)$ 中的大头。

证明：因为 $\left(f_1\left(x\right)+f_2\left(x\right)\right)\left(g_1\left(x\right)+g_2\left(x\right)\right)=f_1\left(x\right)g_1\left(x\right)+\left(f_1\left(x\right)g_2\left(x\right)+f_2\left(x\right)g_1\left(x\right)+f_2\left(x\right)g_2\left(x\right)\right)$，而 $f_1\left(x\right)$ 和 $g_1\left(x\right)$ 分别为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头和 $g_1\left(x\right)+g_2\left(x\right)$ 中的大头，即 $\underset{x\to \ast }{\lim }\frac{f_2\left(x\right)}{f_1\left(x\right)}=\underset{x\to \ast }{\lim }\frac{g_2\left(x\right)}{g_1\left(x\right)}=0$，于是

$\underset{x\to \ast }{\lim }\frac{f_1\left(x\right)g_2\left(x\right)+f_2\left(x\right)g_1\left(x\right)+f_2\left(x\right)g_2\left(x\right)}{f_1\left(x\right)g_1\left(x\right)}=\underset{x\to \ast }{\lim }\left(\frac{g_2\left(x\right)}{g_1\left(x\right)}+\frac{f_2\left(x\right)}{f_1\left(x\right)}+\frac{g_2\left(x\right)}{g_1\left(x\right)}\cdot \frac{f_2\left(x\right)}{f_1\left(x\right)}\right)=0$ ,

即 $f_1\left(x\right)g_1\left(x\right)$ 为当 $x\to \ast$ 时 $\left(f_1\left(x\right)+f_2\left(x\right)\right)\left(g_1\left(x\right)+g_2\left(x\right)\right)$ 中的大头。

推论1若 $f_1\left(x\right)$ 和 $g_1\left(x\right)$ 分别为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头和 $g_1\left(x\right)+g_2\left(x\right)$ 中的大头，则 $r_1{s}_1{f}_1\left(x\right)g_1\left(x\right)\left(r_1{s}_1\ne 0\right)$ 为当 $x\to \ast$ 时 $\left(r_1{f}_1\left(x\right)+r_2{f}_2\left(x\right)\right)\left(s_1{g}_1\left(x\right)+s_2{g}_2\left(x\right)\right)$ 中的大头。

结合性质1和性质2易证，证明略。

性质3若 $f_1\left(x\right)$ 为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头，则对任意 $\alpha \in \text{R}$， ${\left(f_1\left(x\right)\right)}^{\alpha }$ 为当 $x\to \ast$ 时 ${\left(f_1\left(x\right)+f_2\left(x\right)\right)}^{\alpha }$ 中的大头。

证明：因为 $f_1\left(x\right)$ 为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头，即 $\underset{x\to \ast }{\lim }\frac{f_2\left(x\right)}{f_1\left(x\right)}=0$，于是

$\underset{x\to \ast }{\lim }\frac{{\left(f_1\left(x\right)+f_2\left(x\right)\right)}^{\alpha }-{\left(f_1\left(x\right)\right)}^{\alpha }}{{\left(f_1\left(x\right)\right)}^{\alpha }}=\underset{x\to \ast }{\lim }{\left(1+\frac{f_2\left(x\right)}{f_1\left(x\right)}\right)}^{\alpha }-1=0$ ,

即 ${\left(f_1\left(x\right)\right)}^{\alpha }$ 为当 $x\to \ast$ 时 ${\left(f_1\left(x\right)+f_2\left(x\right)\right)}^{\alpha }$ 中的大头。

注1：若 $f_1\left(x\right)$ 和 $g_1\left(x\right)$ 分别为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头和 $g_1\left(x\right)+g_2\left(x\right)$ 中的大头，则 $f_1\left(x\right)+g_1\left(x\right)$ 未必为当 $x\to \ast$ 时 $f_1\left(x\right)+g_1\left(x\right)+f_2\left(x\right)+g_2\left(x\right)$ 中的大头。

例如，取 $f_1\left(x\right)=x+x^3$， $f_2\left(x\right)=x^2$， $g_1\left(x\right)=-x+2x^3$， $g_2\left(x\right)=2x^2$，则不难验证 $f_1\left(x\right)$ 和 $g_1\left(x\right)$ 分别为当 $x\to 0$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头和 $g_1\left(x\right)+g_2\left(x\right)$ 中的大头，但

$\underset{x\to 0}{\lim }\frac{f_2\left(x\right)+g_2\left(x\right)}{f_1\left(x\right)+g_1\left(x\right)}=\underset{x\to 0}{\lim }\frac{3x^2}{3x^3}=\underset{x\to 0}{\lim }\frac{1}{x}=\infty \ne 0$ ,

即 $f_1\left(x\right)+g_1\left(x\right)$ 不是当 $x\to 0$ 时 $f_1\left(x\right)+g_1\left(x\right)+f_2\left(x\right)+g_2\left(x\right)$ 中的大头。

注2：若 $\underset{x\to \ast }{\lim }\frac{f_2\left(x\right)}{f_1\left(x\right)}=0$，则记 $f_1\left(x\right)\gg f_2\left(x\right)$， $x\to \ast$。显然 $x^x\gg a^x\gg x^{\alpha }\gg {\log }_{c}x$， $x^m\gg x^n\left(m>n\right)$， $x\to +\infty$，其中 $a,c>1,\alpha >0$，如图1所示。

定理1若 $f_1\left(x\right)$ 和 $g_1\left(x\right)$ 分别为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头和 $g_1\left(x\right)+g_2\left(x\right)$ 中的大头，则 $\underset{x\to \ast }{\lim }\frac{f_1\left(x\right)+f_2\left(x\right)}{g_1\left(x\right)+g_2\left(x\right)}=\underset{x\to \ast }{\lim }\frac{f_1\left(x\right)}{g_1\left(x\right)}$。

证明：若 $f_1\left(x\right)$ 和 $g_1\left(x\right)$ 分别为当 $x\to \ast$ 时 $f_1\left(x\right)+f_2\left(x\right)$ 中的大头和 $g_1\left(x\right)+g_2\left(x\right)$ 中的大头，则 $\underset{x\to \ast }{\lim }\frac{f_1\left(x\right)+f_2\left(x\right)}{g_1\left(x\right)+g_2\left(x\right)}=\underset{x\to \ast }{\lim }\frac{f_1\left(x\right)\left(1+\frac{f_2\left(x\right)}{f_1\left(x\right)}\right)}{g_1\left(x\right)\left(1+\frac{g_2\left(x\right)}{g_1\left(x\right)}\right)}=\underset{x\to \ast }{\lim }\frac{f_1\left(x\right)}{g_1\left(x\right)}\cdot \underset{x\to \ast }{\lim }\frac{1+\frac{f_2\left(x\right)}{f_1\left(x\right)}}{1+\frac{g_2\left(x\right)}{g_1\left(x\right)}}=\underset{x\to \ast }{\lim }\frac{f_1\left(x\right)}{g_1\left(x\right)}$。

注：可形象称此定理为“抓大头”求极限定理。

推论2 对任意 $m,n\in \text{N}$，有

$\underset{x\to \infty }{\lim }\frac{a_0{x}^m+a_1{x}^{m-1}+a_2{x}^{m-2}+\cdots +a_m}{b_0{x}^n+b_1{x}^{n-1}+b_2{x}^{n-2}+\cdots +b_n}=\underset{x\to \infty }{\lim }\frac{a_0{x}^m}{b_0{x}^n}\left(a_0{b}_0\ne 0\right)$ .

推论3 对任意 ${\alpha }_2>{\alpha }_1>0,{\beta }_2>{\beta }_1>0$，有

$\underset{x\to 0}{\lim }\frac{k_1{x}^{{\alpha }_1}+k_2{x}^{{\alpha }_2}}{l_1{x}^{{\beta }_1}+l_2{x}^{{\beta }_2}}=\underset{x\to 0}{\lim }\frac{k_1{x}^{{\alpha }_1}}{l_1{x}^{{\beta }_1}}\left(k_1{l}_1\ne 0\right)$ .

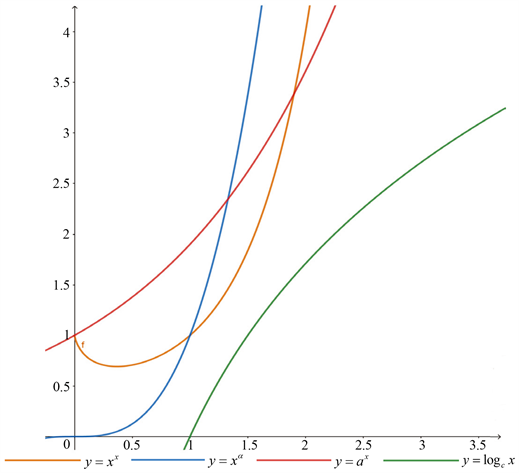
Figure 1. Comparison of four types of functions

图1. 四类函数变化趋势比较

3. “抓大头”思想的应用

这一部分我们将通过一些考研数学中的真题和全国大学生数学竞赛真题等举例说明“抓大头”思想的应用。

例1 (2007年考研数学三) $\underset{x\to \infty }{\lim }\frac{x^3+x^2+1}{2^x+x^3}\left(sinx+\cos x\right)=$ ________。

解：因为 $x^3\gg x^2\gg 1$， $2^x\gg x^3$， $x\to \infty$，所以 $\underset{x\to \infty }{\lim }\frac{x^3+x^2+1}{2^x+x^3}=\underset{x\to \infty }{\lim }\frac{x^3}{2^x}=0$，即 $\frac{x^3+x^2+1}{2^x+x^3}$ 为 $x\to \infty$ 时的无穷小，而 $\left|sinx+\cos x\right|\le \sqrt{2}$，故由有界变量与无穷小的积仍是无穷小的结论可知 $\underset{x\to \infty }{\lim }\frac{x^3+x^2+1}{2^x+x^3}\left(sinx+\cos x\right)=0$，答案为0。

例2 (2010年考研数学一)极限 $\underset{x\to \infty }{\lim }{\left(\frac{x^2}{(x-a)(x+b)}\right)}^x=\left(\right)$。

(A) 1(B) e(C) ${\text{e}}^{a-b}$ (D) ${\text{e}}^{b-a}$

解：首先判断极限的类型。因为 $x\gg -a$， $x\gg b$， $x\to \infty$，所以

$\underset{x\to \infty }{\lim }\frac{x^2}{\left(x-a\right)\left(x+b\right)}=\underset{x\to \infty }{\lim }\frac{x^2}{x\cdot x}=\underset{x\to \infty }{\lim }1=1$ ,

因而原极限属于 ${\text{1}}^{\infty }$ 型，可考虑利用第二重要极限的推广 [5]。注意到 $x\gg -a$， $x\gg b$， $\left(a-b\right)x\gg a+b$， $x\to \infty$，因而

$\underset{x\to \infty }{\lim }{\left(\frac{x^2}{\left(x-a\right)\left(x+b\right)}\right)}^x=\underset{x\to \infty }{\lim }{\left(1+\frac{\left(a-b\right)x+ab}{\left(x-a\right)\left(x+b\right)}\right)}^x={\text{e}}^{\underset{x\to \infty }{\lim }\frac{\left[\left(a-b\right)x+ab\right]x}{\left(x-a\right)\left(x+b\right)}}={\text{e}}^{\underset{x\to \infty }{\lim }\frac{\left(a-b\right)x\cdot x}{x\cdot x}}={\text{e}}^{\underset{x\to \infty }{\lim }\left(a-b\right)}={\text{e}}^{a-b}$ ,

答案为C。

例3 (第三届全国大学生数学竞赛决赛) $\underset{x\to +\infty }{\lim }\left[\left(x^3+\frac{x}{2}-\tan \frac{1}{x}\right){\text{e}}^{\frac{1}{x}}-\sqrt{1+x^6}\right]$。

解：因为 $x^3\gg \frac{x}{2}-\tan \frac{1}{x}$， $x\to +\infty$，所以

$\begin{array}{l}\underset{x\to +\infty }{\lim }\left[\left(x^3+\frac{x}{2}-\tan \frac{1}{x}\right){\text{e}}^{\frac{1}{x}}-\sqrt{1+x^6}\right]=\underset{x\to +\infty }{\lim }\left[x^3{\text{e}}^{\frac{1}{x}}-\sqrt{1+x^6}\right]=\underset{x\to +\infty }{\lim }{x}^3\left[{\text{e}}^{\frac{1}{x}}-\sqrt{1+x^{-6}}\right]\\ \stackrel{x=\frac{1}{t}}{=}\underset{t\to 0^{+}}{\lim }\frac{{\text{e}}^t-\sqrt{1+t^6}}{t^3}=\underset{t\to 0^{+}}{\lim }\frac{{\text{e}}^t-1}{t^3}-\underset{t\to 0^{+}}{\lim }\frac{\sqrt{1+t^6}-1}{t^3}=\underset{t\to 0^{+}}{\lim }\frac{t}{t^3}-\underset{t\to 0^{+}}{\lim }\frac{\frac{1}{2}{t}^6}{t^3}=+\infty -0=+\infty \end{array}$ .

例4 (2015年广东专插本)若当 $x\to 0$ 时 $kx+2x^2+3x^3$ 与x是等价无穷小，则常数 $k=\left(\right)$。

(A) 0(B) 1 (C) 2(D) 3

解：因为当 $k=0$ 时， $2x^2\gg 3x^3$， $x\to 0$，所以 $\underset{x\to 0}{\lim }\frac{kx+2x^2+3x^3}{x}=\underset{x\to 0}{\lim }\frac{2x^2}{x}=\underset{x\to 0}{\lim }2x=0$，显然可知 $k\ne 0$，此时 $kx\gg 2x^2\gg 3x^3$， $x\to 0$，因而 $\underset{x\to 0}{\lim }\frac{kx+2x^2+3x^3}{x}=\underset{x\to 0}{\lim }\frac{kx}{x}=\underset{x\to 0}{\lim }k=k$。

据已知可知 $k=1$ 时，答案为B。

4. 小结

掌握“抓大头”思想对简化极限运算，快速高效求出极限具有非常重要的作用，如何判断多个函数中的大头是关键，因而要熟练掌握。

基金项目

2018年度广西高校中青年教师基础能力提升项目(离散系统理论及应用研究，No. 2018KY0327)，广东理工职业学院2020年“创新强校工程”项目(创新创业教育背景下的《高等数学》在线开放课程建设，No. 2020LGCQ03-01)，广东开放大学基金项目(离散系统动力学研究，No. RC1926)。

NOTES

^*通讯作者。