基于像增强器的紫外光谱探测系统中的噪声分析

Noise Analysis in UV Spectral Detection Systems Based on Image Intensifiers

摘要: 为大幅度提升紫外光谱探测的灵敏度，本文将紫外像增强器与CCD器件耦合而成的紫外ICCD与分光组件再次耦合，构成直读式紫外光谱探测系统，并对其进行研究。设计了基于像增强器的紫外光谱探测系统，并分别对紫外像增强器的噪声和CCD相机的噪声进行了具体分析。研究实验结果表明：曝光时间越长，CCD图像噪声越小，灰度曲线越平滑；反之，曝光时间越短，CCD图像受噪声影响越大，灰度曲线越剧烈。研究发现，帧积分时间的延长，能够有效降低随机噪声，使图像信噪比增高。本文工作为减少噪声对系统的影响从而提高探测效率，极大拓展紫外光谱探测技术的应用领域，同时为微光夜视技术的发展提供依据。

Abstract: In order to substantially improve the sensitivity of UV spectral detection, this paper couples the UV ICCD, which is made by coupling the UV image intensifier and CCD device, with the spectral component again to form a direct reading UV spectral detection system. The UV spectral detection system based on the image intensifier is designed, and the noise of the UV image intensifier and the noise of the CCD camera are specifically analyzed respectively. The experimental results of the study show that the longer the exposure time is, the less noise the CCD image has and the smoother the grey scale curve is; conversely, the shorter the exposure time is, the more the CCD image is affected by noise and the more drastic the grey scale curve is. It is found that the extension of the frame integration time can effectively reduce the random noise and make the image signal-to-noise ratio higher. The work in this paper provides a basis for reducing the impact of noise on the system and thus improving the detection efficiency, greatly expanding the application area of UV spectral detection technology, and providing a basis for the development of micro-optical night vision technology.

1. 引言

紫外探测技术主要是利用工作于紫外波段的探测器件对目标紫外辐射信号实施探测和识别的一种技术，如今已应用于紫外告警、紫外制导、紫外通信、紫外指纹识别以及紫外电晕检测等。紫外像增强器是紫外探测技术的核心探测器件，可将微弱的紫外光图像进行光电转换、电子倍増和电光转换，最终得到亮度增强的可见光图像，提高检测效率。紫外光电探测器主要可分为两大类：光电发射紫外探测器和半导体紫外探测器，如图1所示 [1] [2]。

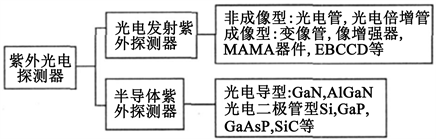
Figure 1. Classification of UV detectors

图1. 紫外探测器分类

紫外像增强器发展至今，技术上已经相对比较成熟，但为了得到更高性能的紫外像增强器，科研人员包括一些研究机构或者公司都在对紫外光电阴极进行改进，力求找到更有效地提高阴极灵敏度，降低噪声的方法。德国ProxiVision公司所生产的紫外像增强器ASB在254 nm处辐射灵敏度可达40 mA/W，等效背景辐射照度可达到10~13 W/m² [3]。以色列OFIL公司采用ASB像增强器，生产了民用电力线电晕检测仪，技术已相当成熟 [4]。英国Photek公司、日本滨松公司、法国Photonis公司等国外知名公司也都有生产日盲紫外像增强器及紫外相关组件，性能与ASB像增强器几乎一致。

而国内的中国电科55所也已经研制出相当水平的紫外增强器并已大量生产使用，北方夜视集团有限公司近年来也在进行日盲紫外像增强器的研究，天津8358研究所 [5]，随着国际紫外技术的发展，国家对紫外探测器件的重视以及国内市场对紫外ICCD发展的需求，经过科研人员的钻研，已取得了巨大进步，不断缩小与国外的先进技术的差距。

然而，目前关于耦合式直读紫外ICCD的光谱探测系统的研究，特别是探测系统的噪声的相关报道甚少。本文对耦合式直读紫外ICCD的光谱探测系统进行了研究，并分析了噪声对探测器灵敏度的影响。

2. ICCD的结构与工作原理

紫外ICCD是由紫外像增强器与可见光CCD成像系统通过中继耦合器件耦合而成的，ICCD的主要组成部分为物镜、像增强器、中继元件和CCD，其中光阴极、微通道板和荧光屏三者构成了像增强器部分，如图2所示 [6] [7]。通过ICCD的物镜的入射光，首先在光阴极上形成了外界目标物体的光学图像；然后，光阴极把接收到的光学信号，通过光电转换作用就变为了电子信号；进入到微通道板中进行倍增后，这些电子信号击打在荧光屏上产生出新的光子信号，它们通过耦合荧光屏和CCD的中继元件到达CCD中，接着CCD把收集到的光子信号通过光电转换作用而变为电子信号，最后从读出电路输出出来。

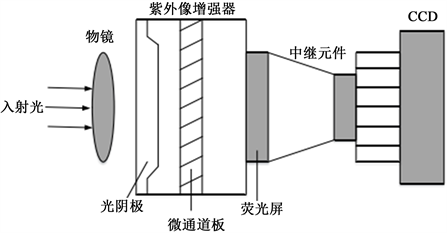
Figure 2. Schematic diagram of UV ICD structure

图2. 紫外ICCD结构示意图

CCD与像增强器之间的耦合中继元件有两类：1) 光纤光锥：光纤光锥的结构为一头大、一头小，它是一种光纤传像器件。2) 中继透镜：这种方式也可耦合像增强器的输出图像到CCD的输入光敏面上，而且容易调节，获得的图像也很清楚，因此，这种耦合的方式对于背照明和前照明的CCD都很适合。

3. 紫外ICCD的噪声模型

紫外ICCD探测图像在诸多方面具有优越性能，但突出的问题是图像噪声较大。在如何去掉噪声之前，必须清楚微光图像噪声产生的机理。本文将从时间域随机过程和空间域随机过程统一的角度来描述ICCD成像系统的噪声模型、来源、信噪比等方面情况，为抑制微光图像噪声奠定基础。

3.1. 图像噪声的基本理论模型

一般地，通常都将电噪声和光学噪声简单地描述为时间域和空间域的随机过程 [8] [9]。在实际成像系统中，也应将图像噪声统一描述为时间域和空间域的随机过程。基于此，本文对于任意时空点(r, t)处图像的量子通量密度的随机起伏，可将图像的时空噪声表述为下列的实列矢量

$n\left(r,t\right)=\left[\begin{array}{c}{n}_r\left(t\right)\\ n_t\left(r\right)\end{array}\right]$ (1)

式中， $n_r\left(t\right)$ 是r点在时间域中均值为零的实随机过程，通常指热噪声、散粒噪声、辐射噪声、温度噪声、产生-复合噪声以及1/f噪声等这些熟知的基本噪声； $n_t\left(r\right)$ 是在t时刻位于空间域中均值为零的实随机过程，是针对那些与结构因素有关系的空间随机不均匀的一类噪声。所以， $n_r\left(t\right)$ 表示的是时间噪声， $n_t\left(r\right)$ 表示的是空间噪声。特别应注意的是，除非时空域之间的转换或空时域之间的转换，一般地，时间噪声 $n_r\left(t\right)$ 只能用时间域滤波器在时间域中滤波，空间噪声 $n_t\left(r\right)$ 也只用空间域滤波器在空域中滤波。

作为一个矢量随机过程，时空噪声 $n\left(r,t\right)$ 的自相关矩阵函数为

$\Phi =\epsilon \left[n\left(r,t\right)n^{\text{T}}\left(r+\rho ,t+\tau \right)\right]$ (2)

亦即

$\Phi =\left[\begin{array}{cc}\epsilon \left[n_r\left(t\right)n_{r+\rho }\left(t+\tau \right)\right]& \epsilon \left[n_r\left(t\right)n_{t+\tau }\left(r+\rho \right)\right]\\ \epsilon \left[n_t\left(r\right)n_{r+\rho }\left(t+\tau \right)\right]& \epsilon \left[n_t\left(r\right)n_{t+\tau }\left(r+\rho \right)\right]\end{array}\right]$ (3)

或

$\Phi =\left[\begin{array}{cc}{\Phi }_{r,r+\rho }\left(t,t+\tau \right)& {\Phi }_{r,t+\tau }\left(t,r+\rho \right)\\ {\Phi }_{t,r+\rho }\left(r,t+\tau \right)& {\Phi }_{t,t+\tau }\left(t,r+\rho \right)\end{array}\right]$ (4)

假设时间噪声与空间噪声无关、彼此独立，即

${\Phi }_{r,t+\tau }\left(t,r+\rho \right)={\Phi }_{t,r+\rho }\left(r,t+\tau \right)=0$ (5)

则有

$\Phi =\left[\begin{array}{cc}{\Phi }_{r,r+\rho }\left(t,t+\tau \right)& 0\\ 0& {\Phi }_{r,r+\tau }\left(r,r+\rho \right)\end{array}\right]$ (6)

假如时间噪声和空间噪声的统计性质分别在时间上和空间上是均匀的，且与坐标和坐标t无关，则有

${\Phi }_{r,r+\rho }\left(t,t+\tau \right)={\Phi }_{r,r}\left(t,t+\tau \right)={\Phi }_1\left(t,t+\tau \right)$ (7)

${\Phi }_{r,r+\tau }\left(r,r+\rho \right)={\Phi }_{r,r}\left(r,r+\rho \right)={\Phi }_2\left(r,r+\rho \right)$ (8)

于是

$\Phi =\left[\begin{array}{cc}{\Phi }_1\left(t,t+\tau \right)& 0\\ 0& {\Phi }_2\left(r,r+\rho \right)\end{array}\right]$ (9)

如果再假定时间噪声和空间噪声均为平稳的随机过程

${\Phi }_1\left(t,t+\tau \right)={\Phi }_1\left(\tau \right)$ (10)

${\Phi }_2\left(r,r+\rho \right)={\Phi }_2\left(\rho \right)$ (11)

则有

$\Phi =\left[\begin{array}{cc}{\Phi }_1\left(\tau \right)& 0\\ 0& {\Phi }_2\left(\rho \right)\end{array}\right]$ (12)

若根据维纳一辛钦定理 [10] [11] [12]，可知相关函数与维纳谱是傅立叶变换对。因此，以v表示时间频率，f表示空间频率，则由式(12)可导出图像的时间域和空间域噪声的维纳谱矩阵

$W\left(v,f\right)=\left[\begin{array}{cc}{W}_1\left(v\right)\delta \left(f\right)& 0\\ 0& W_2\left(f\right)\delta \left(v\right)\end{array}\right]$ (13)

其中， $W_1\left(v\right)$ 表示的是时间域噪声的维纳谱， $W_2\left(f\right)$ 表示的是空间域噪声的维纳谱，即

$W_1\left(v\right)={\displaystyle {\int }_{-\infty }^{\infty }{\Phi }_1\left(\tau \right){\text{e}}^{-2\pi jv\tau }\text{d}\tau }$ (14)

$W_2\left(f\right)={\displaystyle {\int }_{-\infty }^{\infty }{\Phi }_2\left(\rho \right){\text{e}}^{-2\pi jf\rho }\text{d}\rho }$ (15)

并且，也可以推导出图像时间域和空间域噪声的方差矩阵

$V=\left[\begin{array}{cc}{\displaystyle {\int }_{-\infty }^{\infty }{W}_1\left(v\right)\text{d}v}& 0\\ 0& {\displaystyle {\int }_{-\infty }^{\infty }{W}_2\left(f\right)\text{d}f}\end{array}\right]$ (16)

3.2. 系统噪声

假定系统由M个子系统级联组成，若第i级子系统的线倍率为 ${\beta }_i$，则系统总线倍率为

$\beta ={\displaystyle {\cap }_{i=1}^M{\beta }_i}$ (17)

而第 级以后第 $\left(i+1\right)$ 级至第m级后续累积线倍率为

${\beta }_{im}={\displaystyle {\cap }_{j=i+1}^m{\beta }_j}$ (18)

如此令f表示系统输出端的空间频率，则系统的总光学传递函数和总调制传递函数为

$H\left(f\right)={\displaystyle {\cap }_{i=1}^M{H}_i\left({\beta }_{im}f\right)}$ (19)

$M\left(f\right)={\displaystyle {\cap }_{i=1}^M{M}_j\left({\beta }_{im}f\right)}$ (20)

其中， $H_i\left({\beta }_{iM}f\right),M_i\left({\beta }_{im}f\right)$ 分别为第i级子系统的光学传递函数与调制传递函数。若

令 $f_m$ 为第m级子系统输出端的空间频率

$f_m={\beta }_{mM}f$ (21)

那么第 级以后第 $\left(i+1\right)$ 级至第m级的后续累积光学传递函数与调制传递函数则为

$H_{im}\left(f_m\right)={\displaystyle {\cap }_{j=i+1}^m{H}_i\left({\beta }_{jm}{f}_m\right)}$ (22)

$M_{im}\left(f_m\right)={\displaystyle {\cap }_{j=i+1}^m{M}_j\left({\beta }_{jm}{f}_m\right)}$ (23)

同时，令 $g_i$ 表示第i级子系统对入射福射量子通量峰值波长下的增益， ${\alpha }_i$ 表示第i级子系统对入射福射量子通量的光谱匹配因子，则

${\alpha }_i=\frac{{\displaystyle {\int }_0^{\infty }{p}_i\left(\lambda \right){\epsilon }_i\left(\lambda \right)\text{d}\lambda }}{{\displaystyle {\int }_0^{\infty }{p}_i\left(\lambda \right)\text{d}\lambda }}$ (24)

其中， $p_i\left(\lambda \right)$ 为第i级子系统入射辖射量子通量的光谱密度分布， ${\epsilon }_i\left(\lambda \right)$ 为第i级子系统的相对光谱量子效率，则系统的总量子增益为

$G={\displaystyle {\cap }_{i=1}^M{a}_i{g}_i}$ (25)

第i级的后面，第 $\left(i+1\right)$ 级至第m级的后续累积量子增益为

$G_{im}={\displaystyle {\cap }_{j=i+1}^m{a}_j{g}_j}$ (26)

那么，首先考虑级M级联系统的空间噪声。除输入图像本身可能己经叠加有空间噪声外，级联的每个子系统都有可能引入了新的空间噪声。按功率相加的原则，系统输出端总空间噪声的维纳谱应为

$W_2\left(f\right)={\displaystyle {\sum }_{i=0}^M{W}_{2i}\left({\beta }_{iM}f\right)G_{iM}^2{M}_{IM}^2\left(f\right)}$ (27)

其中， $W_{2i}\left({\beta }_{iM}f\right)$ 为第i级子系统引入的空间噪声在其输出端的维纳谱， $W_{20}\left({\beta }_{0M}f\right)$ 为系统输入图像原有空间噪声的维纳谱。且约定： ${\beta }_{MM}=G_{MM}=M_{MM}\left(f\right)=1$。在写出上式时，实际上假定了系统中一切噪声源所产生的噪声，都是相加性噪声(即噪声是叠加在信号上的)。同时，还假定噪声与信号系统是无关的，不同的噪声源所产生的噪声之间也是彼此独立的、不相关的。

包含第级在内的第级以前的系统累积空间噪声的维纳谱则为

$W_{2ic}\left(f_i\right)={\displaystyle {\sum }_{j=0}^i{W}_{2i}\left({\beta }_{ji}{f}_i\right)G_{ji}^2{M}_{ji}^2\left(f_i\right)}$ (28)

$W_1\left(v\right)={\displaystyle {\sum }_{i=0}^M{W}_{1i}\left(v\right)G_{iM}^2{M}_{iM}^2\left(v\right)}$ (29)

其中， $W_{1i}\left(v\right)$ 为第i级子系统引入的时间噪声在其输出端的维纳谱， $W_{10}\left(v\right)$ 为系统输入图像原有时间噪声的维纳谱， $M_{im}\left(v\right)$ 为第i级后的系统后续累积时间域调制传递函数

$M_{iM}\left(v\right)={\displaystyle {\cap }_{j=i+1}^m{M}_j\left(v\right)}$ (30)

$M_j\left(v\right)$ 为第j级子系统的时间域调制传递函数。且有类似约定： $G_{MM}=M_{MM}\left(v\right)=1$。包括为第级在内的第 级以前系统累积时间噪声的维纳谱则为

$W_{1ic}\left(v\right)={\displaystyle {\sum }_{j=0}^i{W}_{1j}\left(v\right)G_{ji}^2{M}_{ji}^2\left(v\right)}$ (31)

其中， $M_{ji}\left(v\right)$ 为第j级后的第 $\left(j+1\right)$ 级至第i级的后续累积时间域调制传递函数

$M_{ji}\left(v\right)={\displaystyle {\cap }_{q=j+1}^i{M}_q\left(v\right)}$ (32)

由于维纳谱表示的是噪声功率谱密度，则作为噪声功率的方差为

${\sigma }_2^2={\displaystyle {\int }_{-\infty }^{\infty }{W}_2\left(f\right)\text{d}f}$ (33)

${\sigma }_1^2={\displaystyle {\int }_{-\infty }^{\infty }{W}_1\left(v\right)\text{d}f}$ (34)

${\sigma }_{2ic}^2={\displaystyle {\int }_{-\infty }^{\infty }{W}_{2ic}\left(f_i\right)\text{d}{f}_i}$ (35)

${\sigma }_{1ic}^2={\displaystyle {\int }_{-\infty }^{\infty }{W}_{1ic}\left(v\right)\text{d}v}$ (36)

且在空间噪声与时间噪声统计无关的情况下，则有

${\sigma }^2={\sigma }_2^2+{\sigma }_2^2$ (37)

${\sigma }_{ic}^2={\sigma }_{2ic}^2+{\sigma }_{1ic}^2$ (38)

表征系统噪声的另一常用参数为噪声因子。噪声因子F，定义为系统输入功率信噪比与输出功率信噪比之比，或系统总噪声引起的部分方差之比。即

$F=\frac{\left(SNR\right)p_{1in}}{\left(SNR\right)p_{2out}}=\frac{{\sigma }_{sot}^2}{{\sigma }_{par}^2}$ (39)

因此，对于空间噪声，第i级子系统的噪声因子有

$F_{2i}=\frac{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^i{W}_{2j}\left({\beta }_{ji}{f}_i\right)G_{ji}^2{M}_{ji}^2\left(f_i\right)\text{d}{f}_i}}}{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^{i-1}{W}_{2j}\left({\beta }_{ji}{f}_i\right)G_{ji}^2{M}_{ji}^2\left(f_i\right)\text{d}{f}_i}}}=1+\frac{{\sigma }_{2i}^2}{g_{i{a}_2}^2{\sigma }_{2\left(i-1\right)c}^2}$ (40)

其中，

${\sigma }_{2i}^2={\displaystyle {\int }_{-\infty }^{\infty }{W}_{2i}\left(f_i\right)\text{d}{f}_i}$ (41)

是第i级子系统引入的空间噪声在其输出端的方差；

是第i级子系统输入空间噪声的方差，即为包括第 $i-1$ 级在内第 $i-1$ 级以前系统累积空间噪声的方差；

是第i级子系统输入空间噪声传递至第i级子系统输出端时的方差与第i级子系统输入空间噪声的方差之比

$g_{i{\sigma }_2}^2=\frac{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^{i-1}{W}_{2i}\left({\beta }_{ji}{f}_i\right)G_{ji}^2{M}_{ji}^2\left(f_i\right)\text{d}{f}_i}}}{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^{i-1}{W}_{2j}\left({\beta }_{j\left(i-1\right)}{f}_{i-1}\right)G_{j\left(i-1\right)}^2{M}_{j\left(i-1\right)}^2\left(f_{i-1}\right)\text{d}{f}_{i-1}}}}$ (42)

M级级联系统对于空间噪声的总噪声因子为

$F_2={\displaystyle {\cap }_{i=1}^M{F}_{2i}}$ (43)

而对于时间噪声，则第i级子系统的噪声因子为

$F_{1i}=\frac{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^i{W}_{1j}\left(v\right)G_{ji}^2{M}_{ji}^2\left(v\right)\text{d}v}}}{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^{i-1}{W}_{1j}\left(v\right)G_{ji}^2{M}_{ji}^2\left(v\right)\text{d}v}}}=1+\frac{{\sigma }_{1i}^2}{g_{i{\sigma }_1}^2{\sigma }_{1\left(i-1\right)c}^2}$ (44)

其中，

${\sigma }_{1i}^2={\displaystyle {\int }_{-\infty }^{\infty }{W}_{1i}\left(v\right)\text{d}v}$ (45)

是第i级子系统引入的时间噪声在其输出端的方差；是第i级子系统输入时间噪声的方差，即为包括

第 $i-1$ 级在内第 $i-1$ 级以前系统累积时间噪声的方差； $g_{i{\sigma }_1}^2$ 是第i级子系统输入时间噪声传递至第i级子

系统输出端的方差与第级子系统输入时间噪声的方差之比

$g_{i{\sigma }_1}^2=\frac{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^{i-1}{W}_{1j}\left(v\right)G_{ji}^2\left(v\right)M_{ji}^2\left(v\right)\text{d}v}}}{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\sum }_{j=0}^{i-1}{W}_{1j}\left(v\right)G_{j\left(i-1\right)}^2{M}_{j\left(i-1\right)}^2\left(v\right)\text{d}v}}}$ (46)

M级级联系统对于时间噪声的总噪声因子为

$F_1={\displaystyle {\cap }_{i=1}^M{F}_{1i}}$ (47)

上述关于系统噪声的讨论，是建立在量子通量密度的随机涨落 $n\left(r,t\right)$ 基础之上的。对于任一分辨单元a在抽样时间 $\tau$ 内积累的量子数目上叠加的随机涨落 $N\left(a,\tau \right)$，只要注意到 $n\left(r,t\right)$ 与 $N\left(a,\tau \right)$ 在统计性质上有如下确定关系

${\sigma }_{1N}^2={\displaystyle {\int }_{\left|l\right|\le \tau }{\displaystyle {\int }_{r\in a}{\displaystyle {\int }_{-\infty }^{\infty }{W}_{1n}\left(f\right)\text{d}f\text{d}r\text{d}t}}}$ (48)

${\sigma }_{2N}^2={\displaystyle {\int }_{\left|l\right|\le \tau }{\displaystyle {\int }_{r\in a}{\displaystyle {\int }_{-\infty }^{\infty }{W}_{2n}\left(f\right)\text{d}f\text{d}r\text{d}t}}}$ (49)

就可以使用关于 $n\left(r,t\right)$ 所讨论的任何结果。

4. 噪声分析与讨论

事实上，根据微光成像系统的结构和工作机理可以确定噪声的主要来源于MCP的影像增强器(也称像管)的噪声和CCD本身的噪声，而像增强器的噪声对于成像质量的影响更大。下面具体分析。像管所接收的入射光子、光电阴极出射的光电子、微通道板的倍增电子、荧光屏输出光子都具有量子性，都可视为离散的随机过程 [13] [14]。

4.1. 光电阴极产生的噪声

由入射光子数的涨落导致发射光电子数的涨落所引起的噪声可表示为：

$N_{c1}=\sqrt{\bar{n}A\tau {\eta }_c}$ (50)

式中 ${\eta }_c$，为光电阴极的量子效率。

光电阴极的量子效率 ${\eta }_c$ 具有泊松分布几率，这是由光电阴极发射本身的随机性所决定的，可将产生的光电子噪声 $N_{c2}$ 表示为：

$N_{c2}=\sqrt{\bar{n}A\tau {\eta }_c}$ (51)

式(50)，(51)的两项噪声线性无关，则所得的光电阴极光电子发射总量子噪声 $N_c$ 为

$N_c=\sqrt{N_{c1}^2+N_{c2}^2}=\sqrt{\bar{n}A\tau {\eta }_c^2+\bar{n}A\tau {\eta }_c}$ (52)

由于不同的光电阴极的量子效率 $\eta$ 不一样，当 $\eta$ 远小于1时，忽略 $\eta$ 的平均项，则有

$N_c=\sqrt{\bar{n}A\tau {\eta }_c}$ (53)

上式表明光电阴极的光电子发射的量子噪声是主要因素，光子的噪声的影响甚微，可忽略不计。

4.2. 微通道板电子倍增过程产生的噪声

1) 当微通道板没有输入信号时，仍然存在输出，一般称谓背景噪声。它是由工作电压所产生的场强导致通道内壁产生了微弱的场致发射，然后经后继的倍增变为大的输出而产生的。它有通道内壁的材料性质、工作电压和表面状态所决定。在系统中，它和光阴极的发射电流相比，要小两个数量级，也可以不计算在内。

2) 当微通道板有信号输入时，大体上有三种情况会导致微通道板的输出信号产生噪声(也就是增益起伏的变化)。

① 微通道板输入端的开口面积是有限的，这就可能使得随机变化的入射电子不能落入开口面积而被阻隔，造成部分入射电子的损失。

② 随机变化的入射电子并不是总能得到倍增，当它们的运动方向与通道轴线平行时，就直接穿过通道。

③ 由于通道内被倍增的二次电子的数目会随每个二次电子的出射角以及初量的不同而有所不同，逸出几率也与多种因素相关，其输出中伴随有量子噪声。

总而言之，微通道板倍增电子噪声的大小可表示为：

$N_m=\sqrt{\bar{n}A\tau {\eta }_c{P}_0{G}^2+\bar{n}A\tau {\eta }_c{P}_0\eta \left[\frac{1+\delta }{\delta }+\frac{P\left(1+\delta \right)}{\delta P-1}\right]G^2}$ (54)

公式中的第一项是由于输入到微通道板的光电子数本身所具有的涨落而引起的输出电子噪声，公式子中的第二项是由微通道板的多级二次电子倍增的随机涨落而引起的输出电子噪声。两者相比，后者大于前者。

4.3. 荧光屏上的光子噪声

微光ICCD像管荧光屏发射出的光子数所引起的量子涨落情况，大体有以下两个方面 [15]：

1) 轰击到荧光屏上的电子数具有涨落变化，因此引起了输出光子噪声 $N_{S1}$。

2) 经测量和理论分析证明，荧光屏发光本身的量子效率是一个符合泊松分布律的离散变量。它所引起的噪声为 $N_{S2}$。

综合计算上述两项噪声，则荧光屏输出光子的总量子涨落噪声( $N_S$ )为

$N_S=\sqrt{N_{S1}^2+N_{S2}^2}=\sqrt{\bar{n}A\tau {\eta }_c\eta P_0{G}^2\left[1+\frac{1+\delta }{\delta }+\frac{P\left(1+\delta \right)}{\delta P-1}\right]\left({\eta }_s^2+{\eta }_s\right)}$ (55)

由于荧光屏的量子效率 ${\eta }_s$ 远大于1，可将式(55)中的 ${\eta }_s$ 一次方项略去，即

$N_S\approx \sqrt{\bar{n}A\tau {\eta }_c\eta P_0{G}^2\left[1+\frac{1+\delta }{\delta }+\frac{P\left(1+\delta \right)}{\delta P-1}\right]{\eta }_s^2}$ (56)

它表明像管的总量子噪声主要是光电阴极的量子噪声和微通道板的噪声。

4.4. 荧光屏上表现出的颗粒噪声

荧光屏的发光特性会受它的空间上的非均匀性结构所限制。当电子不断地击打荧光屏使它产生新的光子时，它所输出的光分布呈现出颗粒状的亮点闪烁，常将这一噪声称谓荧光屏颗粒噪声，用输出的光子数表示为：

$N_g=\sqrt{\bar{n}A\tau {\eta }_c\eta P_0\overline{{\beta }^2\left(x,y\right)}}G{\eta }_s$ (57)

其中， $\overline{{\beta }^2\left(x,y\right)}$ 的数值通常是取一定的像元面积作为采样窗口来实测荧光屏的光出射度，再由计算确定。对分辨率为201 p/mm的等效像元来说，此 $\overline{{\beta }^2\left(x,y\right)}$ 的实际值约为(0.015)²。

4.5. CCD本身的噪声

一般来说，CCD本身的噪声主要指的是光子散粒噪声、暗电流噪声以及读出噪声 [15] [16]。

1) 光子散粒噪声

光子入射到成像区光敏面是一个随机过程，是一束不连续的光子流，而且是独立的、均匀的。光敏面接收到的光子数目在单位时间内不是一成不变的，它围绕均值有微小旳变化。光子散粒嗓声就是由这种微小的变化所形成的。

2) 暗电流噪声

没有加光信号和电信号的CCD仍有电流，它是在MOS电容器处于深耗尽状态，被收集在势讲中的有热激发产生的少数载流子所形成，常把这个电流称为暗电流。它是导致暗白点、白色损伤或颗粒的原因，也是决定像质的重要因素。暗电流噪声的大小与温度有关，还与点荷包在势讲中存储的时间长短有关，暗电流噪声随存储时间越长而越大。

3) 读出噪声

读出噪声主要是复位噪声和1/f噪声，其中，复位噪声也叫KTC噪声。它主要来源于输出放大器和后续处理电路，且呈高斯分布状态。

a) 复位噪声

微光ICCD的输出结构通常釆用浮置扩散放大器，其输出结构如图3所示，信号电荷通过浮置电容变成相应的电压输出。T₁是复位MOS场效应管，它的漏极接到复位电平上；D是输出二极管，在反偏电压状态下工作；T₂是读出MOS场效应管，也可以称为电压跟随器；C为浮置扩散电容，它的作用就是能存储电荷。

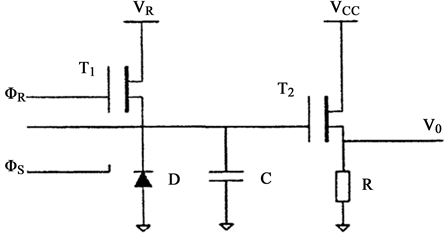
Figure 3. Output structure diagram of floating diffusion amplifier

图3. 浮置扩散放大器的输出结构图

在每个像素的输出过程中，由于输出二极管D都工作在强反偏的状态下，因此电容C被充电至高电平V_R，在复位脉冲Φ_R为正时，场效应管T₁导通，读出场效应管T₂的输出电平V₀被复位至V_R电平上，为接受下一个电荷包做准备。当Φ_R正脉冲截止时，T₁也截止。

在时钟驱动下，出现脉冲Φ_S时，到达输出端的信号电荷开始对电容C进行充电，电容C的电压就下降。随之下降的还有T₂的输出电平V₀，降幅形成了输出信号电压。当输出信号被后续电路采集后，电容C开始放电，为下一个像素的电荷转换做准备。在此过程中，复位MOS管T₁反复在导通和切断状态下工作。当T₁工作在导通状态时，会产生导通沟道电阻R，电容C两端遇到电阻R热噪声会干扰输出信号，常将此热噪声称为复位噪声。复位整个过程可视为复位管漏极电压V_R经由电阻R对电容C进行充电的过程，如图4所示。在RC电路的带限作用下，电容C两端的噪声已不再是白噪声。另外，RC的等效噪声带宽可知为 $\Delta f_e=1/4RC$，电容C两端的噪声电压的均方值可由下式计算得到

$\overline{V_n^2}=4kTR\Delta f_e=kT/C$ (58)

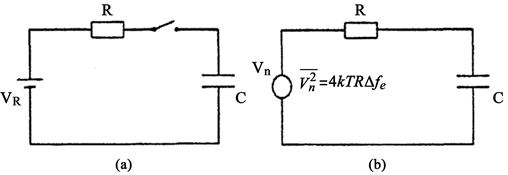
Figure 4. Output noise equivalent circuit

图4. 输出噪声等效电路

其中，T为绝对温度，k为波尔兹曼常数。换算噪声电压为电子数，则有

$\Delta n=\sqrt{kTC}/e$ (59)

复位噪声也称为KTC噪声。并且，复位噪声会随着浮置扩散电容的变大而变大。通过采用相关釆样法(CDS)可以减小复位噪声，它的原理如图5所示。在输出参考电平和信号电平时，由于等效电容C上噪声电压的涨落是缓慢的，因此可使得两次采样S₁和S₂在一个像素周期内完成，并且两次采样的时间间隔也比时间常数RC小得多，这样噪声电压在两次采样中就无太大的差别，可认为两次取样的时间是相关的。复位噪声可以通过两次采样值的相减运算得以滤除，运算结果所得的差值就是实际的有用信号。

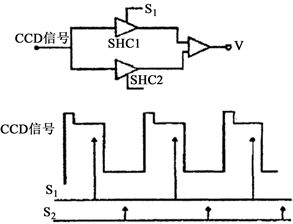
Figure 5. Principle circuit and timing waveform of correlated double sampling

图5. 相关双采样的原理电路及时序波形

b) 低频噪声(1/f噪声)

经验表明，低频噪声是半导体器件在有电流流过时产生的，但目前不清楚它的原因。最新的研究结果指出，低频噪声产生的原因主要是PN结空间电荷区和周围的陷阱对载流子的复合和发射所导致的。在表面进入耗尽状态后，由于表面势的增加而导致噪声亦随之迅速上升，并且在将要反型时会形成一个峰值，易知通过PN结的电流I与1/f噪声频谱 $S_I\left(f\right)$ 存在如下关系

$S_I\left(f\right)\propto I^{\beta }$ (60)

其中，体分量 $\beta \approx 1$，表面分量 $\beta \approx 2$。

5. 结果与讨论

为验证高速检测的可行性，进行了不同CCD曝光时间的对比测试。从不同曝光时间曲线中可以看出，曝光时间越长，图像的信噪比越高，帧积分时间的延长，能够有效降低随机噪声，这也就是常规光谱仪在检测较弱光谱辐射时，采用长至数秒积分时间的原因。

在成像系统中，消除随机噪声的最佳方法就是利用帧平均，但是帧平均是利用噪声信号时域不相关特性实现的 [17]。如果噪声信号具有空间不相关特性，那么就可以利用面阵CCD的多行信号实现平滑降噪，为验证这个思想，我们抽取100 ms曝光图像中40行信号，进行平均处理，处理结果如图6~8所示，可见对光谱信号进行行平均，具有明显的降噪效果。氘灯光谱中的特征谱线清晰可见。

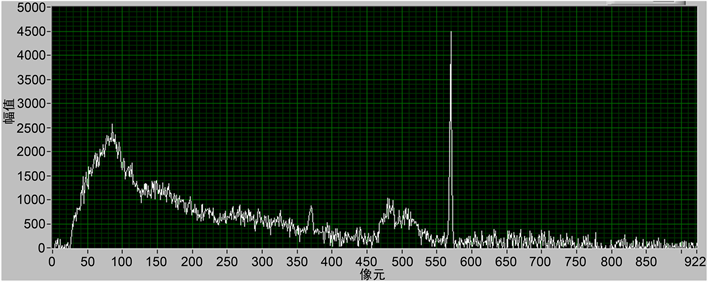
Figure 6. Image and gray scale curve with 100 ms exposure time

图6. 曝光时间100 ms图像及灰度曲线

Figure 7. Image and gray scale curve with 10 ms exposure time

图7. 曝光时间10 ms图像及灰度曲线

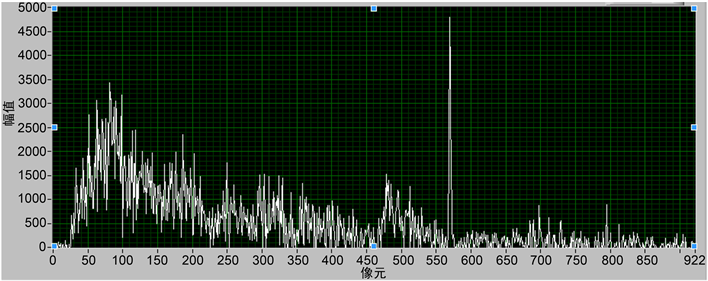
Figure 8. Image and gray scale curve with 1 ms exposure time

图8. 曝光时间1 ms图像及灰度曲线

进行平滑处理后的图像对比(图9~11)：

Figure 9. The result of smoothing the gray-scale curve with 100 ms exposure time

图9. 曝光时间100 ms灰度曲线平滑处理结果

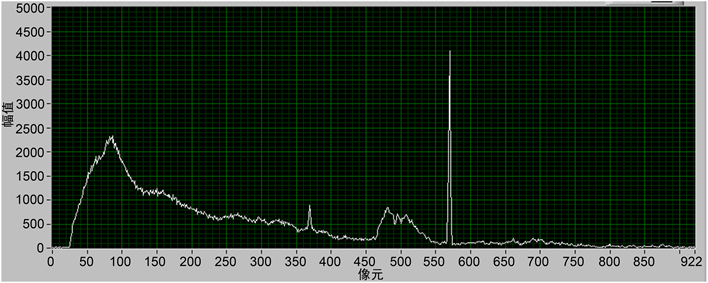
Figure 10. The result of smoothing the gray-scale curve with 10 ms exposure time

图10. 曝光时间10 ms灰度曲线平滑处理结果

Figure 11. The result of smoothing the gray-scale curve with 1 ms exposure time

图11. 曝光时间1 ms灰度曲线平滑处理结果

在系统设计中采用全局曝光CCD进行数据采集，可以将曝光时间缩短至微秒级，采用高分辨率CCD进行数据采集，能够实现数百甚至1000行数据的平滑处理，将获得很高的信噪比，从而实现高速光谱数据获取；针对低强度光谱数据探测，可以延长曝光时间，这样也将获得比常规线阵探测器信噪比高得多的光谱曲线。

6. 结论

为了研究噪声对紫外系统探测能力的影响，将紫外像增强器与CCD器件耦合而成的紫外ICCD与分光组件再次耦合，构成直读式紫外光谱探测系统，经过实验分析得知，系统各组件部分的光电转换中都存在着不同程度的噪声，输出图像质量受到噪声的干扰而降低。因此降低噪声对直读式紫外探测系统的影响进而提升紫外ICCD的成像质量具有良好的应用前景。

NOTES

^*通讯作者。