1. 引言
当前,随着航空运输业的快速发展,空中交通需求不断增加,空域拥挤现象日益严重,机场航班延误现象日益频繁,管制员保障压力也更为繁重。从当前的种种问题中我们发现,空中交通运行的规划部门与管理部门,亟需采取有效的空域管理以及流量管控技术,从而实现空域资源的科学调整以及空域流量的合理分配,进一步优化繁忙机场的航班时刻质量,从而减轻一线管制员的工作负荷,通过积极采取相关措施实现空管系统的转型升级,最终全面提升系统的运行效能。
从上世纪90年代,很多学者就逐渐认识到空中交通系统的复杂性特征,并对其进行了研究。在空管系统的相关研究中,复杂性一直以多种多样的形式存在:空中交通复杂性、空域复杂性、管制复杂性、认知复杂性、交通流复杂性等,虽然名称不同,侧重点略有区别,但在研究内容和方法上存在着一定的共性:分析空域内复杂交通行为的影响因素,提炼复杂性指标,建立指标体系,构建评估方法。因此,梳理已有成果中的复杂性指标对于归纳扇区交通行为的影响要素,量化分析扇区交通行为具有基础性的支撑作用。一直以来,航空器数量/密度都是反映交通行为最基础、最常用的指标。在美国,将15分钟间隔内最大航空器数量设为峰值航空数量,为流量管理机构提供决策支持,例如基于该指标决定是否采取改航策略[1]。在欧洲,流量管理人员依据扇区内航空器数量与容量的匹配情况评估交通负荷,进而决定开扇或合扇;增强的交通管理系统便是利用流量预测值与扇区所能接收最大航空器数量对比,提供辅助决策[2]。在1995年,航空无线电技术委员会(RTCA, Radio Technical Commission for Aeronautics)首次提出“动态密度”概念,用于定量描述空域复杂性,涉及交通密度、间隔标准和交通流复杂性等因素[3]。在2001年,G. B. Chatterji等认为空域复杂性是空域结构和交通流相互作用的结果,但空域结构一般相对稳定,而交通流复杂性可以通过航空器架次、航空器对间隔分布、爬升/下降/平飞航空器比例、速度混杂比、相对速度、平均冲突预计时间、最小冲突预计时间、冲突解脱难度等16个指标反映[4]。在2010年,Jelena Djokic等在总结前人研究的基础上,选取了24个复杂性因素,包含航空器数量、冲突次数、航空器对的汇聚/离散角度、状态改变的航空器数量等,反映管制扇区内的复杂交通行为[5]。在2013年,Markus Vogel等列举了19个描述空域复杂性的因素,包括航空器数量、航空器数量的平方、爬升/下降航空器数量、改变航向/速度的航空器数量、冲突水平距离、冲突垂直距离等[6]。在2015年,Toy构建了两种扇区交通行为复杂性评估模型,一种借鉴动态密度的建模思路,包含航空器数量、平均加权水平间隔的倒数、最小水平间隔的倒数、速度标准差、平均冲突解脱难度等因素,另一种是基于航迹度量复杂性,考虑扇区面积、天气影响、违反标准间隔等因素;分析结果表明基于航迹的复杂性能够粗略反映管制工作负荷,这在未来基于4维航迹的运行环境中可以发挥更大的作用[7]。
本文借鉴已有成果,从密度性、动态性和冲突性三个维度,归纳并总结了描述扇区交通行为的指标体系,以指标为定量分析交通行为的载体,以国内某区域管理中心多个扇区为样本,通过实际历史数据,基于统计指标的时间序列,利用改进的K-medoids聚类算法,识别多个扇区在不同交通行为下的分布模式和变化规律。
2. 扇区交通行为模式指标体系
2.1. 指标体系构建
虽然空中交通管制领域给出的部门交通行为的表述大多是经验性的,但对于理解和全面描述部门交通行为仍有借鉴意义。因此,本章是在现有研究成果的基础上,结合交通运行的基本特征,从新的角度,直接选取有助于定量描述该部门交通行为的指标,或者对能够合理量化的原始指标进行分解和筛选描述了空中交通系统运行状况指标部分作为一个新的指标,建立了一个代表该部门交通行为的指标体系。所选指标有明确的数学定义,对空域单位具有更普遍的适用范围。根据交通行为指标的描述维度,将交通行为指标分为密度、动态和冲突三类。
密度类指标包括:1、航空器数量;2、航空器数量与容量的比值(简称容流比);3、管制里程;4、管制时间。
动态类指标包括:5、航向改变超过15度的航空器数量;6、速度改变超过10节的航空器数量;7、高度改变超过750英尺的航空器数量;8、航空器的平均速度。
冲突类指标包括:9、水平最小间隔;10、垂直最小间隔;11、追越冲突航空器对数量;12、对头冲突航空器对数量。
2.1.1. 密度类指标
密度指标主要用于描述该部门飞机的分布情况,可以大致反映该部门在一定时期内的总体运输情况以及飞机在空间中的聚集状态。在实际的空中交通管制工作中,空中交通管制的难度通常根据部门交通的密度特征来衡量,这是部门交通行为的最基本,最直观的体现。
1、航空器数量
若航空器
,
表示时段
内在扇区Sec中运行的航空器集合,则扇区航空器数量
可表示为:
(1)
2、容流比
若时段
内扇区Sec中航空器数量为
,扇区容量为
,则容流比
可表示为:
(2)
3、管制里程
若
表示
的管制飞行里程,则时段
内扇区Sec中所有航班的管制飞行里程
可具体表示为:
(3)
4、管制时间
若
表示
的管制飞行时间,则时段
内扇区Sec中所有航班的管制飞行时间
可具体表示为:
(4)
2.1.2. 动态类指标
在实际运行过程中,由于管制员经常向该部门管制下的飞机发出操纵指令,例如调整速度,改变高度,偏航等,因此该部门的交通行为也表现出更大的动态性,成为导致流量复杂性和管制员工作负荷提升的因素。因此,动态指标主要用于描述交通行为的动态特征。
5、航向改变的航空器数量
若
表示航向改变大于15?的航空器,
表示时段
内扇区Sec中所有航向改变大于15?的航空器集合,则该指标
可表示为:
(5)
6、速度改变的航空器数量
若
表示速度改变超过10节的航空器,
表示时段
内扇区Sec中所有速度改变大于10节的航空器集合,则该指标
可表示为:
(6)
7、高度改变的航空器数量
若
表示高度改变超过2000英尺的航空器,
表示时段
内扇区Sec中所有高度改变的航空器集合,则该指标
可表示为:
(7)
8、平均速度
若
的速度为
,则在时段
内扇区Sec中所有航空器的平均速度
可表示为:
(8)
2.1.3. 冲突类指标
冲突指标主要基于扇区内飞机对之间的相对位置分布关系,描述飞机之间潜在的飞行冲突。在实际的空中交通管制工作当中,由于不确定因素的存在,使飞机无法在航路网络中准确地执行预定的飞行计划,导致它们在非常接近的空间范围内相遇。当飞机接近足以造成危险的临界范围时,定义为飞行冲突。由于管制员的冲突缓解干预,实际冲突很少发生,但潜在的飞行冲突却较为普遍的存在与实际工作当中,是管制工作需要关注的焦点。冲突指标能够充分反映飞机之间的耦合效应,反映部门交通行为的临界特征,间接反映管制员的工作负荷。
9、水平最小间隔
若航空器
与
水平间隔为
,
,则在时段
内扇区Sec中的水平最小间隔
可表示为:
(9)
10、垂直最小间隔
若航空器
与
垂直间隔为
,
,则在时段
内扇区Sec中的垂直最小间隔
可表示为:
(10)
11、追越冲突航空器对数量
管制员一般较易处理垂直截获冲突,而难以处理小于30?汇聚角的冲突或对头冲突(汇聚角大于165?小于180?)。若
表示航空器对
的航迹交叉角,在时段
扇区Sec内具有潜在追越冲突的航空器对数量
可表示为:
(11)
(12)
12、对头冲突航空器对数量
与指标22类似,在时段
内扇区Sec中具有潜在对头冲突的航空器对数量
可表示为:
(13)
(14)
2.2. 交通行为模式分析方法
2.2.1. 基于DTW的K-medoids聚类算法
聚类是一个将整体数据划分为以类或簇存在的包含局部数据对象的过程,来源于数据挖掘、统计学、机器学习等众多领域,现在已经广泛应用于模式识别、数据分析以及图像处理等领域[8]。K-means是一种广泛使用的经典划分式聚类算法,可以高效地对大型数据集进行分类,且计算复杂度低,运算速度快。但是,该算法也有一些缺点,例如对“噪声”和离群值(离群值)敏感,无法预先确定聚类数。为了改进K-means算法,Kaufmam和Rousseeuw设计了k-medoids算法[9]。在K-means算法中,质心用于表示聚类簇,这使其对噪声和异常数据非常敏感,但聚类簇由最靠近中心(中心点)的对象表示,可以有效地消除这种影响。因此,本章使用k-medoids聚类算法分析部门交通行为指标数据,以提高处理异常值的能力。
当聚类分析的对象是高维、复杂的时间序列时,主要的处理方式可分为三类:基于原始数据的聚类、基于特征的聚类以及基于模型的聚类。其中基于特征的处理方式源于降维的思想,压缩和提炼原始数据,平滑噪声,然后在新的特征空间中进行聚类,已有方法包括离散傅里叶变换(DFT)、离散小波变换(DWT)、奇异值分解(SVD),该方法虽然数据压缩的效率很高,但对平行偏移、线性偏移、振幅变换、不连续性等都比较敏感,并且特征值缺乏数据原有的实际意义,降低了可理解性。基于模型的度量是指首先对时间序列进行建模,然后通过模型参数等信息对数据进行聚类,常用模型包括自回归移动平均模型(ARMA)、隐马尔科夫模型(HMM)、人工神经网络模型(ANN)等[10],但在实际情况中,时间序列常常很难用一个具体的模型来表示,此外为了增加聚类的准确性,建模难度也会大大提高,以上种种均限制了该类方法的应用。而基于原始数据的聚类则不会对时间序列做任何处理,欧氏距离是常用的相似性度量方法,但欧氏距离对于异常数据较为敏感。因此,国外学者提出了动态时间弯曲距离(Dynamic time warping,DTW) [11]作为一种新的相似性度量方法,通过调节时间点之间的对应关系,能够寻找两个任意长时间序列中数据之间的最佳匹配路径,对噪声有很强的鲁棒性,可以更有效地度量时间序列的相似性。由于DTW距离不要求两个时间序列中的点一一对应,因此具有更广的适用范围。但不可否认的是,DTW时间复杂度更高,计算代价较为昂贵[12]。
2.2.2. 聚类有效性评价
聚类算法通常需要预先指定所需的聚类数量,但是在大多数情况下,需要优化最佳聚类数。尽管经验法则证明K小于样本数的平方根,但是仍然有必要进一步锁定K值以提高K-medoids聚类算法的性能。确定最佳群集数的问题属于群集有效性的问题。聚类有效性评价指标用于衡量聚类算法产生的聚类结果是否达到最佳标准。这种索引将与最佳聚类结果相对应的聚类数作为最佳聚类数。参照先前的研究结果,DB (Davies bouldin)和Dunn指数可以计算出同一类别中样本的接近度以及样本在不同类别中的离散度:Dunn指数越大,聚类效果越好;DB索引越小,聚类效果越好。因此,将Dunn/DB用作新的聚类有效性评估指标。索引值越大,聚类效果越好,从而确定最佳的聚类数量。
3. 实例验证分析
选取国内某区域管制中心的多个扇区作为分析对象。区管中心所辖扇区共有24个扇区,以高空扇区为主高度范围主要在7800米以上。考虑到当前从管制部门自动化系统提取的数据存在缺失的情况,在经过了数据筛选、过滤以及清洗工作之后,选择数据保存质量较为完好的15个扇区(Sector1-Sector15)作为扇区交通特征聚类研究的样本,并选取了保存质量较好的某天的实际运行历史数据,计算扇区样本的各项指标。
3.1. 基于单一指标的扇区交通行为聚类分析
基于指标体系各个指标的时间序列,对统计范围内的所有扇区中航班的交通特征进行分析。考虑到,空中交通系统的时段性运行特征,在8:00前的时段航班较少,故而导致统计指标多为零值,因此本文选取全天中航班较多的时段(8:00~23:00),选取5 mins作为统计粒度,进行指标时间序列的计算。结合一线实际管制工作经验,从各类指标中选取关注度较高的作为典型代表,分析基于不同交通行为下的模式聚类结果。密度类指标选用了航空器数量,动态类指标选取速度改变航空器数量以及平均速度,冲突类指标选用了追越冲突航空器对数量。基于时间序列的分析可以更加聚焦某一具体的交通行为,通过扇区样本在较长时间范围内的行为展现整体的分布趋势。
3.1.1. 密度类指标的交通行为聚类分析
密度类指标的分析基于航空器数量的时间序列数据,开展15个扇区的聚类分析。聚类方法为基于DTW的K-medoids算法,并且在完成聚类后,进一步利用Dunn/DB评估K-medoids算法的聚类结果。由于时间序列相对较长,故而借鉴经验准则,分析当聚类数量在2-4之间变化时对应的聚类质量,评价结果如表1所示,聚类效果最佳时的聚类数量为4,具体的聚类结果表述如下:第一类:Sector 8/12;第二类:Sector 2/11;第三类:Sector 1/3/6/7/9/10/13;第四类:Sector 4/5/14/15。

Table 1. Clustering evaluation results based on the number of aircraft
表1. 基于航空器数量的聚类评价结果
为了直观的体现各是扇区指标的分布状况,避免数据过多过长对于分析结果表达的干扰,本文选取了各类结果的聚类中心,针对不同类样本数据展开对比说明。
四类扇区的聚类中心如图1所示,以阴影框出部分作为例证片段数据。第一类扇区的飞机数量逐渐增多并且呈现为长期保持稳定水平的状态,之后自第76个时段以来逐渐减少,总的来说第一类扇区中的航空器数量在长期处于四个类别中最多的状态。第二类扇区则在第一个小时内处于以5个航空器架次为幅度的振荡状态,在接下来的一个小时内,航空器的数量呈现为先缓慢降到一个波底然后缓慢下降上升的态势,类似于SIN函数的分布特征。第三类扇区上升到峰值比较快,然后在短暂下降后缓慢上升到较高水平,并且与第一类相同从第76个时段开始逐渐减少;第四区的飞机长期处于低位,航空器数量一般维持在1左右,远低于其他类别。然而,前三类行业往往相互交织,并不总是遵循1类 > 2类 > 3类的趋势。聚类结果较好地识别了不同扇区在飞机数量上的分布规律。
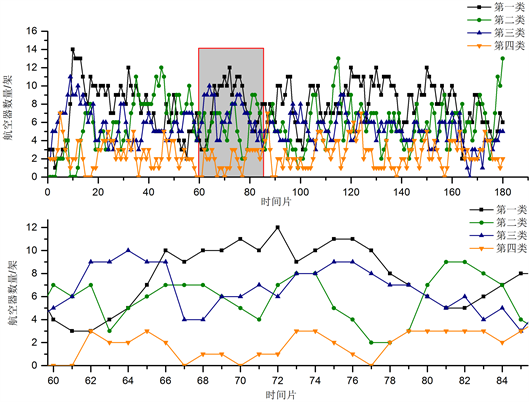
Figure 1. Cluster center of sector samples of the number of aircraft
图1. 航空器数量的扇区样本聚类中心
3.1.2. 动态类指标的交通行为聚类分析
1、速度改变的航空器数量
速度改变航空器数量指标在15个扇区中的聚类评价结果如表2所示,聚类效果最佳时的聚类数量为4,具体的聚类结果表述如下:第一类:Sector 12;第二类:Sector 1/9/10;第三类:Sector 2/3/8/11/13;第四类:Sector4/5/6/7/14/15。

Table 2. Clustering evaluation results of aircraft number with speed change
表2. 速度改变的航空器数量聚类评价结果
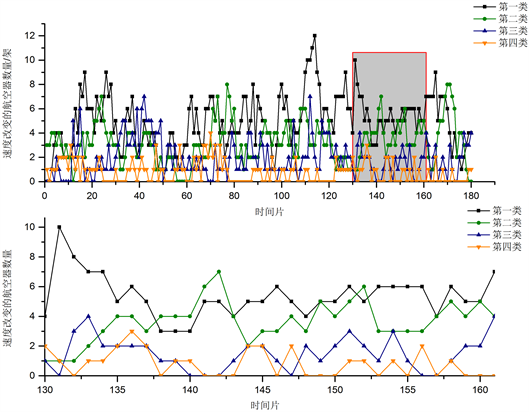
Figure 2. Cluster center of sector samples of the number of aircrafts with velocity change
图2. 速度改变的航空器数量的扇区样本聚类中心
同样的,速度变化航空器数量指标仍然采取了聚类中心的展示方法。如图2所示,该指标下不同聚类中心的分布相互交叉,随机选取第130~160个时间片的数据进行放大观察。第一类和第二类扇区的数量分布特征较为接近,并且在一些时间片上表现出“对称”与“一致”共存的分布特征。而第三类和第四类扇区的则是在变化趋势上较为相似,但三四类样本的指标值明显低于第一类和第二类样本,其中大多数不超过两个,曲线“徘徊”在一个左右。
2、平均速度
平均速度指标在15个扇区中的聚类评价结果如表3所示,聚类效果最佳时的聚类数量为4,具体的聚类结果表述如下:第一类:Sector 1/3/5/6/8/11/12/13;第二类:Sector 7;第三类:Sector 2/4/10/14/15;第四类:Sector 9。

Table 3. Clustering evaluation results based on average speed
表3. 基于平均速度的聚类评价结果
如图3所示,平均速度指标的分布趋势相较于密度类指标层次更为清晰,由于平均速度在每个类别中的波动均较小,航空器平均速度由高到低分布在全部样本数据便可以进行区分。随机截取第20~45时间片的局部数据,我们发现该时段内的平均速度变化特征与整体水平一致,呈现为稳定且区分度较高的状态。但值得注意的是,动态类中的指标的聚类结果存在部分重叠的状况,使用不同的流量详细信息,我们可以为扇区流量行为识别不同的模式。当我们扩大到更大的宏观水平时,在微观细节的“结果力量”下,部门交通行为自然会衍生出新的模式。
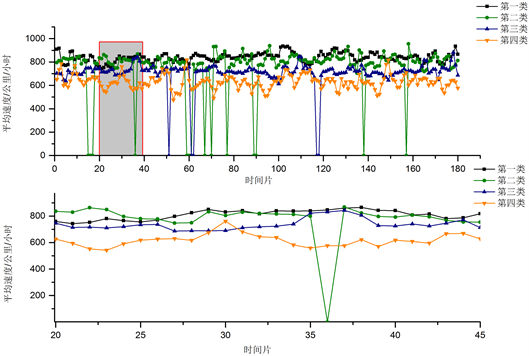
Figure 3. Clustering centers of sector samples with average speed
图3. 平均速度的扇区样本聚类中心
3.1.3. 冲突类指标的交通行为聚类分析
扇区追越冲突航空器在15个扇区中的聚类评价结果如表4所示,与上面两类不同的是,聚类效果最佳时的聚类数量为3,具体的聚类结果表述如下:第一类:Sector 2/11/12;第二类:Sector 1;第三类:Sector 3/4/5/6/7/8/9/10/13/14/15。

Table 4. Quantitative clustering evaluation results of aircraft pairs based on overtaking conflict
表4. 基于追越冲突航空器对数量聚类评价结果
从图4所示的分布特征中我们发现,总的来说,第一类和第二类在大部分时间片中指标较为接近,且远高于第三类指标数值。以第三类指标时间序列数值较高的时段(60~86)为例,开展细节分析,总的来说,第三类扇区中追越冲突航空器对数量呈现为中间高,两端低的凸形分布态势,且在第70~78时间片中远高于其它两类。第一类扇区从整体上来看,追越冲突航空器对数量大于其他扇区,但仅在40分钟的时间范围内呈上升趋势,随后便开始下降并一直保持较低水平。第二类扇区的分布特征则较为特别,其在指标数值呈现为先平稳,直至最后时段开始陡增至峰值后开始下降的分布态势。冲突类指标与其它两类指标相比,着重关注空中交通航空器即将发生冲突时的监控和分析,然而在统计数据当中,这种情况的发生概率较小,故而基于追越航空器数量的聚类分析放大了数据的细节特征,出现了较多扇区聚为1类的情况。
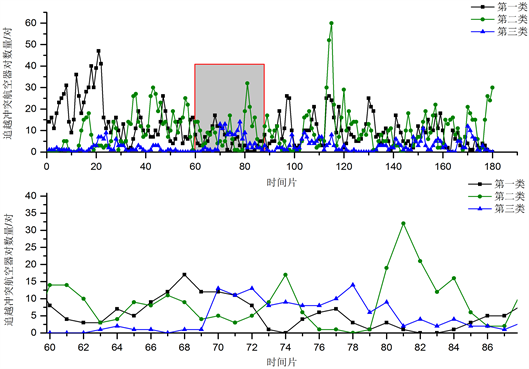
Figure 4. Cluster centers of sector samples for the number of conflicting aircraft pairs
图4. 追越冲突航空器对数量的扇区样本聚类中心
本文通过不同交通行为指标的时间序列,反映了扇区运行过程中不同的特征,在将时间序列的变化趋势纳入考量的同时将扇区进行分类,同一类别的扇区代表了在某个单一交通行为中存在共性。单个指标时间序列的分析结果聚焦于扇区的某个运行特征,从各个方面独立且详细的描述了扇区的运行态势。但是目前,空中交通管理部门往往立足于宏观视角进行空域管理以及空中交通流量管理的策略制定,忽略了实际运行中沉淀的运行数据当中所蕴含的海量信息,进一步深入挖掘数据当中所反映的扇区交通行为特征,掌握空域运行的历史演化趋势并将类似趋势的扇区进行统一划分管理,便可以更加有效且有针对性地开展扇区优化以及流量管理工作。这不仅可以提升空管系统的决策能力,还将进一步分析空域运行的瓶颈,提升空域运行效能,例如效率、安全、复杂性等。
4. 总结
本文选取密度类、动态类和冲突类三个指标类别,构建了描述扇区交通行为的指标体系。基于实际运行数据分析了我国空中交通管制单位15个扇区的交通行为模式。根据管制工作的实际经验甄选指标,建立指标时间序列,并采用基于DTW的K-Medoids聚类算法,识别每个交通特征指标所表达的扇区运行行为模式和变化规律。聚类结果显示,基于DTW的K-Medoids聚类算法对于扇区运行特征指标的时间序列处理的聚类效果较好,实现了对于扇区运行特征更加全面且详细的描述。本文基于扇区的运行特征,从相对微观的角度丰富了对空中交通系统中交通行为的研究。聚类分析的结果有助于管理者全面监控各部门的运行情况,建立灵活的空域管理机制,提高空域运行效率。研究结果也为交通行为模式的自动识别奠定了基础。
基金项目
2020民航安全能力建设基金《机场协同决策(A-CDM)技术规范》项目支持。