1. 引言
20世纪80年代,Lailly,Tarantola等 [1] [2] 分别提出了时间域地震波形反演方法,为全波形反演研究奠定了理论基础。全波形反演(Full Waveform Inversion,简写为FWI)能够充分利用地震波场的全部信息,极大地提高了地震成像的分辨率 [3]。FWI通过拟合模拟数据与观测数据,使得合成波场与观测数据残差达到最小。
经典FWI的目标函数定义为
(1)
其中,
表示
范数,m为反演参数(例如波速、介质密度等),
为震源个数,
表示实际观测数据,
为合成波场,且满足波动方程
(2)
其中,
为波动微分算子。因此,FWI问题为一个标准的偏微分方程(PDE)约束的优化问题。
考虑到FWI大规模计算难题,求解PDE约束的优化问题(1)通常基于梯度型优化方法,如基于一阶梯度信息的最速下降法、非共轭梯度法(NCG) [4]、基于曲率信息的拟牛顿法等 [5]。随着硬件计算能力的不断提高以及实际生产对复杂地质结构高分辨率成像的需求,基于二阶梯度信息的牛顿型方法尤其是截断牛顿法逐渐受到科研人员的重视 [6] [7] [8]。相较于一阶梯度信息反演方法,牛顿型方法对于复杂介质模型(如,盐丘模型,高速度比模型等)和多次散射波场问题具有很好的重构能力,是一种理想的全波形反演方法。
在截断牛顿法求解过程中,为了降低方法对初值的依赖性,通常采用线搜索全局化策略来获取迭代步长。非精确单调线搜索和非单调线搜索是求解步长的理想方法。然而,FWI是一类高度非线性反演问题,目标函数(1)往往高度非线性且不适定,因此在采用单调线搜索获取步长时(目标函数值每一步迭代都单调下降) [9],易使反演方法陷入局部极值,大大降低算法的计算效率。为了提高求解高度非线性优化问题的收敛速度,Grippo等人 [10] 在1986年提出了一种非单调线搜索框架,Hager等人在2004年进一步发展了非单调线搜索方法,该类线搜索在解决复杂问题时表现了优越的计算效率 [11] [12] [13]。因此,基于非单调的线搜索方法求解FWI问题是一种合理选择。截断牛顿法求解FWI问题的另外一个挑战是求解大规模牛顿线性方程组,基于线性共轭梯度法(CG)近似求解牛顿方程的截断牛顿法(CG-NEWTON)已成为求解FWI问题的标准牛顿型方法。然而随着勘探难度的增大,传统线性CG法很难利用Hessian阵的负特征值的信息 [14] [15] [16],降低方法的计算效率。
本文首先回顾截断牛顿FWI反演方法,从理论上分析了单调与非单调线搜索方法各自的性质。其次,为了有效处理Hessian阵的负特征值难题,基于Lanczos对角化技术,给出了相应的截断牛顿反演方法(CG_NEWTON)。针对大规模计算,基于伴随法构建了一种高效计算Hessian阵与向量相乘的方法并基于消息传递接口(Message Passing Interface,简写为MPI)并行实现本文提出的算法。最后,基于Sigsbee模型 [17],从数值角度验证本文提出方法的有效性,并对单调与非单调线搜索算法进行对比试验,以验证基于非单调线搜索方法的高效性。
2. 理论与方法
2.1. 截断牛顿法
对于全波形反演的极小化问题
牛顿法的主要思想是利用二次函数
去逐点近似或逼近目标函数
。在点
附近,对
进行二阶Taylor展开有
其中,
,
表示目标泛函
在点
处的梯度,
为目标函数的Hessian阵。对
关于
求导并令其导数为零,得
(3)
线性方程(2)称为牛顿方程。若
为非奇异阵,则有
于是牛顿迭代公式为
(4)
其中,
表示迭代步长,
称为牛顿下降方向。
FWI是大规模反演问题,采用矩阵分解方法直接求解牛顿方程(3)是不现实的。一方面,Hessian矩阵
通常无法显式计算;另一方面,即便获得了
,采用直接法求解(3)也是不切实际的。因此,通常用CG法来近似求解牛顿方程(3),该方法的最大优点是在求解过程中只需要计算Hessian矩阵与向量的乘积。该类方法称为截断牛顿法(或不精确牛顿法)。算法1所示为一般截断牛顿型方法的算法描述。
在迭代公式(4)中,下降方向
满足
同时,
还需满足充分下降条件
其中
是常数。当下降方向
确定后,
的选取十分重要。在线搜索方法中,步长
的选取有着相应的标准,根据步长是否精确,把线搜索分为精确线搜索和非精确线搜索。在非精确线搜索方法中,根据目标函数值在每步迭代过程中是否单调下降,将线搜索方法分为单调和非单调线搜索方法。本文只讨论非精确线搜索方法。
2.2. 单调线搜索方法
若步长
的取值能够使目标函数
得到一个可接受的下降量
满足这种条件的线搜索称为非精确线搜索。Wolfe准则是一种常见的非精确线搜索步长规则,不仅要求函数值下降,而且对函数值下降量有一定的要求,即
(5)
(6)
其中,
,
。(5)保证了目标函数值序列
单调下降,(6)为曲率条件,保证步长不能太小。Wolfe准则要求目标函数的每一步迭代都是单调下降的,满足
称这样的步长选取方法为单调线搜索。算法2所示为本文实现的Wolfe型单调线搜索的算法描述。
2.3. 非单调线搜索方法
单调线搜索方法要求目标函数在每次迭代过程中严格下降。针对高度非线性、不适定性问题,这样的限制过于苛刻。一维函数具有多局部极值的函数图像如图1所示。
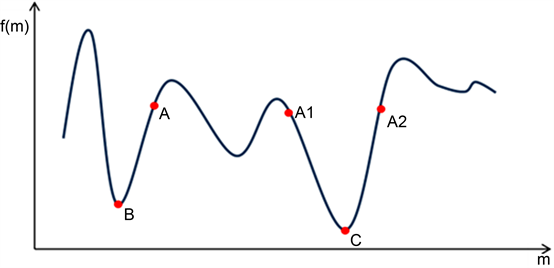
Figure 1. Multiple minima for one dimension
图1. 一维多局部极值示意图
当目标函数位于A点时,为了保证迭代的单调下降性,单调线搜索方法会使目标函数沿着峡谷下降至B点。此时搜索在谷底缓慢前行,步长很小,导致目标函数陷入局部极值,很难到达全局最优解C点。而非单调线搜索方法不要求目标函数的每一步迭代都单调下降,即在某些迭代步允许目标函数出现波动,只需保持总体呈下降趋势即可,使得其步长的选取更具有灵活性。因此,当目标函数位于A点时,非单调线搜索方法能够跳跃至A1点或A2点,最终到达全局最优解C点。
非单调线搜索技术已经得到了广泛应用。一种改进的非单调线搜索准则为在Wolfe条件中将(5)替换为 [13]
(7)
其中,
(8)
在(7)中,
是函数值
的一个凸组合,
的选择控制非单调性的程度。如果
,就是通常的单调Wolfe线搜索。如果
,则
,其中
是函数的平均值。在算法实现中,取
,算法3所示为非单调线搜索算法描述。这种非单调Wolfe线搜索算法不仅能够计算出更大的步长因子,而且还比单调Wolfe线搜索算法和传统的非单调线搜索算法平均使用更少的函数和梯度,极大地提高了算法的收敛速度和计算效率。
2.4. Lanczos对角化法
将线性方程(3)改写成如下形式:
对矩阵
进Lanczos三对角化 [18],即
这里
是使
的正实数。记矩阵
为
矩阵
为
的前l行l列组成的方正,则由Lanczos过程可知
为非奇异对称三对角阵,且
于是Lanczos对角化过程可以改写为如下矩阵紧凑形式
且
的列是标准正交的。当
时Lanczos过程停止,此时有
其中,
表示第一个元素为1其余元素为0的l维向量。设
满足
(9)
于是(3)的解为
采用矩阵分解的直接法求解(9)并引入辅助变量便得到Lanczos版本的线性共轭梯度法 [19]。
2.5. 快速计算矩阵与向量乘积
针对FWI大规模计算问题,采用有限差分法求解Hessian阵显然不现实(因为需要求解与反演参数元素相同次数的波动方程,对于大规模反演问题这是无法承受的)。考虑到CG法只需要计算Hessian阵与向量的乘积。因此,它不需要直接计算Hessian阵巨大的计算量和海量的内存存储。为了行文方便,以下公式推导均省略迭代步索引k。为了高效计算Hessian阵与向量的乘积,对波动方程(3)关于参数m进行两次微分并利用微分链式法则有
(10)
(11)
对任意向量
,对目标函数(1)关于m进行两次微分并将(10)与(11)式代入得
(12)
式中,
(13)
(14)
在方程(13)和(14)中,
表示微分算子
的伴随算子,(13)、(14)分别称为一阶、二阶伴随状态方程。公式(12)表明,计算Hessian阵与向量乘积只需要四次波场模拟:两次正演波场和两次伴随波场。因此,利用伴随状态方法计算Hessian阵与向量的乘积是非常高效的。
3. 数值实验
本节基于频率域声波方程,选取Sigsbee 模型,在频率域进行速度参数反演,从数值计算角度验证提出的CG_NEWTON全波形反演方法的收敛性和可行性,并对比了单调线搜索算法和非单调线搜索算法,验证基于非单调线搜索在求解FWI问题上的优越性。
在频率域中,声波方程(2)的具体形式为
(15)
其中,
表示Laplace算子,h为频率,m表示声波在介质中的传播速度。为了高精度求解数值波动方程(15),引入完全匹配层吸收边界条件(PML) [20],采用高精度交错网格差分格式对该波动方程进行离散,并采用基于稀疏矩阵的并行LU分解求解所得的大规模线性方程组 [21] [22]。
Sigsbee模型
Sigsbee模型拥有复杂的盐丘形状,且顶部构造分界面存在着强烈的速度间断。由于高速盐丘与沉积物的高速度比以及沉积物的渐变结构,因此会有很强的多次散射波场,使得精确反演该模型比较困难。Sigsbee速度模型如图2所示,图2(a)为真实速度模型,图2(b)为初始速度模型,模型离散网格大小为411 × 164,空间采样步长为
。97个震源和390个接收点均匀分布在模型上表面,震源类型为单位脉冲震源。初始模型采用光滑化真实模型而得。从图2中可以看出,初始速度模型未能包括真实速度模型的宏观构造。因此,初始模型的合成波场与观测数据在相位和走时信息存在明显差异,给反演方法带来了挑战。
 (a) Sigsbee真实速度模型
(a) Sigsbee真实速度模型  (b) Sigsbee初始速度模型
(b) Sigsbee初始速度模型
Figure 2. Sigsbee velocity model
图2. Sigsbee速度模型
 (a) 收敛曲线
(a) 收敛曲线 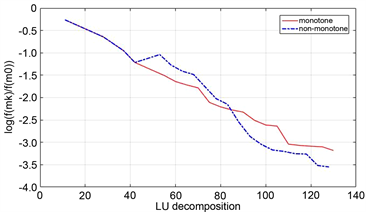 (b) 目标泛函对LU分解次数的变化曲线
(b) 目标泛函对LU分解次数的变化曲线
Figure 3. Curve: The change of the objective function
图3. 目标函数变化曲线
在反演过程中,选取10个频率分别为2.5 Hz, 3.0 Hz, 4.0 Hz, 5.5 Hz, 7.0 Hz, 9.0 Hz, 10.5 Hz, 12.0 Hz, 15.0 Hz, 17.0 Hz。采用从低频到高频的反演策略,单调线搜索方法和非单调线搜索方法每个频率的最大迭代步数都为20步。频率为2.5 Hz时单调与非单调线搜索方法的收敛曲线(a)以及目标函数对于LU分解次数的变化曲线(b)如图3所示。图3表明基于非单调线搜索方法的CG_NEWTON全波形反演方法在收敛速度和计算效率方面优于单调线搜索的CG_NEWTON全波形反演方法。
对Sigsbee模型进行CG_NEWTON全波形反演,重构结果如图4所示,图4(a)为基于单调线搜索的重构结果,图4(b)为非单调线搜索反演重构结果。从图4中可以看出,单调与非单调线搜索都能很好重构出Sigsbee模型,说明本文提出的CG_NEWTON方法是有效的。
 (a) CG单调重构结果
(a) CG单调重构结果 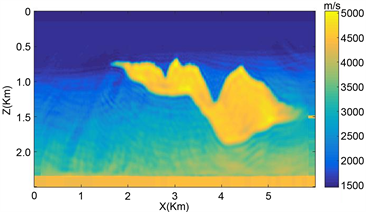 (b) CG非单调重构结果
(b) CG非单调重构结果
Figure 4. Inversion reconstruction results
图4. 反演重构结果
为了显示非单调线搜索方法在计算效率方面的优势,对单调线搜索方法和非单调线搜索方法的迭代步数、LU分解次数、最后一个目标函数值与最初目标函数值的比值进行对比,见表1。从表中可知,非单调线搜索方法需要较少的LU分解次数。表1定量表明,相对于单调线搜索方法,非单线搜索方法具有较好的计算效率和重构分辨率。

Table 1. Comparison between monotone line search method and non-monotone line search method for Sigsbee model in iteration steps, LU decomposition times,
表1. Sigsbee模型,单调线搜索和非单调线搜索方法迭代步数、LU分解次数、
对比
4. 结论
FWI反问题是非线性数学物理反问题,其高度非线性使得常规反演方法易陷入局部极值,很难获得高分辨率的反演结果。同时,大规模的计算资源需求给传统反演方法带来了挑战。本文基于线搜索全局化策略、Lanczos对角化方法建立了利用二阶梯度信息的快速CG_NEWTON反演方法。为了进一步提高算法的计算效率,基于伴随方法导出了一种高效计算Hessian阵与向量相乘的方法。基于Sigsbee高模型进行数值实验,数值结果表明基于单调线搜索与非单调线搜索均能有效重构高速度比的盐丘体,说明了CG_NEWTON方法能够充分利用多散射波场,提高重构分辨率;相对于单调线搜索方法,非单调线搜索方法在求解高度非线性FWI反问题时在收敛速度和计算效率方面更加优越。此外,本文给出的方法具有一般性,能适用于其它成像问题。
基金项目
本文获得国家自然科学基金项目(11801111),贵州省科技计划项目(20191122)资助。