基于BP神经网络的压电智能旋翼主动减振仿真分析

Simulation Analysis of Active Vibration Reduction of Piezoelectric Intelligent Rotor Based on BP Neural Network

摘要: 为提高搜救飞行器在突发外力干扰下依旧可以保持平稳运行的能力，以自身调节机制来迅速响应和适应外力冲击实现主动减振的压电复合材料设计了智能旋翼结构；基于BP神经网络算法的PID控制方法，建立了压电智能旋翼主动减振控制模型；利用Matlab/Simulink平台，通过神经网络算法对偏航角、横滚角、俯仰角三个参数动态调整从而实现飞行过程中对飞行器实时控制。最后在考虑实际飞行控制状态下进行了控制仿真试验。结果表明，该主动减振控制方法，具有带扰动补偿的反馈控制作用，可以有效抑制旋翼在飞行过程中产生的振动，减振效果可提高15%~30%。

Abstract: In order to improve the ability of search and rescue aircraft to maintain stable operation even under sudden external interference, an intelligent rotor structure is designed based on the piezo-electric composite material that uses its own adjustment mechanism to quickly respond and adapt to external impacts to achieve active vibration control method; piezoelectric intelligent rotor active vibration reduction model has been established based on PID control method of BP neural network algorithm; Achieve real-time control of the aircraft during flight by adjusting dynamically yaw angle, roll angle and pitch angle using BP Network, using Simulink module. Finally, a control simulation test is carried out considering the actual flight control state. The results show that the active vibration reduction control method has a feedback control function with disturbance compensation, which can effectively suppress the vibration of the rotor during flight, and the vibration reduction effect can be increased by 15%~30%.

1. 引言

旋翼飞行器具有搜救速度快、覆盖面积广、机动性强、可以有效降低搜救人员受伤率等优点。然而，大雨等恶劣的搜救环境下，飞行器会受外力冲击(如突风扰动)产生振动，导致飞行器失衡甚至旋翼结构破坏，进而导致搜救飞行器坠落等情况的发生，不仅会造成巨大的经济损失，还在一定程度给搜救工作带来极大的不便甚至人员伤害。因此，提高搜救飞行器在突发外力干扰下依旧可以保持平稳运行的能力，是飞行器研发中亟待解决的关键问题之一 [1] [2]。

压电复合材料具有体积轻便、能耗低、频带宽、驱动力高、组合多样、生产和制备技术较成熟等特点，并且具有正逆压电效应，既可以用作作动器又可以作传感器，是目前应用最广泛的一种智能材料。Bailey [3] 等最早利用压电材料结合控制理论开展了一系列主动减振研究。Hu [4] 等提出主动鲁棒性的控制方法对标准的二次控制器和非线性控制信号进行设计研究。丛聪 [5] 等通过建立力学模型对风力机叶片面内的振动建模和控制问题开展研究。Brillante [6] 等基于空气动力学模型和转子模型研究了两种周期性控制方法实现减少直升机旋翼的振动。研究表明，将压电复合材料应用于飞行器旋翼上，通过其自身调节机制来迅速响应和适应外力冲击，具有一定的主动抑振的作用。苑凯华 [7] 等利用大变形应变–位移关系建立非线性模型对复合材料壁板颤振的控制进行了仿真研究。张凤云 [8] 采用压电纤维复合材料MFC作为驱动器，研究悬臂梁的扭转控制问题。压电智能结构是由压电材料作为传感元件和致动元件以及结构本体所组成的智能结构。在智能结构中传感元件用来监测结构的振动，受到微电子系统控制作用致动元件准确动作，结构振动状态因而被改变，随之而来便产生了压电智能结构的振动主动抑制技术，并且有着非常重要的应用前景和应用价值 [9] [10]。

综合现有压电主动减振的研究，本文提出采用压电传感器、压电作动器和控制器组成的在“抑振”方面的压电主动控制策略。基于神经网络PID控制算法，在多模态控制过程中，具有较精确的控制策略，在更短的时间内比常规的PID控制效果提高达15%~25%。该种自适应控制方法，能够较好地在参数不确定的情况下保证系统的鲁棒性。仿真结果表明，该主动减振控制方法能够较好地消除或抑制旋翼机构振动，总体减振效果可达55%~80%左右。

2. 压电智能旋翼结构的耦合模型

2.1. 数值模型

采用压电复合材料建立的压电作动器和传感器为同位配置，可形成最小相位系统以保证控制的稳定性，所建立的压电智能旋翼结构如图1所示。旋翼的有效长度为L_a，厚度为t，在旋翼的上下表面对称粘贴m 对压电片，每对中分别包含作为传感和作动元件的压电片，其厚度均为t_a，第i对压电片的左端到固定端旋转轴的距离为x_i1 ，右端到旋转轴的距离为x_i2，且压电片的宽度为b。假设将片粘贴于旋翼时并不考虑其粘贴层对结构振动特性的影响，且压电材料各向同性且极化方向为z向。

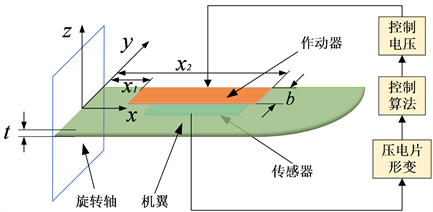
Figure 1. Piezoelectric intelligent rotor structure

图1. 压电智能旋翼结构

当施加电压到压电作动器上时，旋翼的运动方程可表示为：

$E_a{I}_a\frac{{\partial }^4\omega }{\partial x^4}+{\rho }_a{A}_a\frac{{\partial }^2\omega }{\partial t^2}-b{\displaystyle {\sum }_{i=1}^m\frac{{\partial }^2{M}_i^e}{\partial x^2}}=0$ (1)

式中，ω为旋翼的结构位移；E_a为旋翼结构的杨氏模量；I_a = bt³/12 为旋翼结构的惯性矩；ρ_a为旋翼结构的密度；A_a 为旋翼结构的截面积；M_i为第i个压电作动器上产生的力矩。

即

$E_a{I}_a\frac{{\partial }^4\omega }{\partial x^4}+{\rho }_a{A}_a\frac{{\partial }^2\omega }{\partial t^2}={\displaystyle {\sum }_{i=1}^m{k}_a{U}_i^e}\left[\ddot{H}\left(x-x_{i2}\right)-\ddot{H}\left(x-x_{i1}\right)\right]$ (2)

式中，k_a为压电耦合系数； $U_i^e$ 为第i个作动器的控制电压。

当对压电智能旋翼结构的前n阶模态利用模态截断方法进行分析时，其结构位移w的表达式如下所示：

$\omega \left(x,t\right)={\displaystyle {\sum }_{j=1}^n{\phi }_j\left(x\right){\eta }_j\left(t\right)}$ (3)

其中φ_j(x) 为第j阶振型函数，η_j(t) 表示在t时刻下压电智能旋翼结构的模态幅值，整理上式可得：

${\ddot{\eta }}_j\left(t\right)+2{\xi }_j{\omega }_j{\stackrel{\dot{}}{\eta }}_j+{\omega }_j^2{\eta }_j\left(t\right)={\displaystyle {\sum }_{i=1}^m{k}_a\left[{\stackrel{\dot{}}{\phi }}_j\left(x_{i2}\right)-{\stackrel{\dot{}}{\phi }}_j\left(x_{i1}\right)\right]U_i^{\theta }\left(t\right)}$ (4)

这里ω_j和ξ_j分别是第j阶模态的固有频率和阻尼比， $j=\text{1},\text{2},\text{3},\cdots ,n$， $i=\text{1},\text{2},\text{3},\cdots ,m$。引入状态变量 $X={\left[{\eta }_1,{\eta }_2,\cdots ,{\eta }_n,{\stackrel{\dot{}}{\eta }}_1,{\stackrel{\dot{}}{\eta }}_2,\cdots ,{\stackrel{\dot{}}{\eta }}_n\right]}^{\text{T}}$，可得：

$\{\begin{array}{l}\stackrel{\dot{}}{X}=AX+B{U}_a\\ y=U_s=CX\end{array}$ (5)

其中， $A=\left[\begin{array}{cc}{0}_{n\times n}& I_{n\times n}\\ -{\Omega }^2& -2\xi \Omega \end{array}\right]$， $B=\left[\begin{array}{c}{0}_{n\times n}\\ \bar{B}\end{array}\right]$， $C=\left[\begin{array}{cc}\bar{C}& 0_{n\times n}\end{array}\right]$。

2.2. 动力学模型

在建立四旋翼飞行器的动力学模型之前，需要建立地面参考坐标系和机体坐标系，如图2所示为地面参考坐标系和机体坐标系。

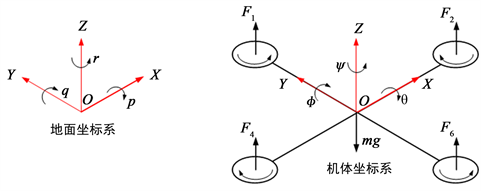
Figure 2. Ground reference coordinate system and Airframe coordinate system

图2. 地面参考坐标系和机体坐标系

因为四旋翼是欠驱动的控制系统，当通过四个电机实现飞行器的机动，不可能直接对这六个自由度进行控制。通过选择升力F₁、横滚力矩F₂、俯仰力矩F₃、偏航力矩F₄这四个可控变量，可以实现控制解耦。控制通道分别对应三个姿态角和四旋翼的高度，四旋翼的水平位移也可以由这四个量解出。由此可推导出机体坐标系与惯性坐标系之间的转换矩阵R为：

$\begin{array}{l}R=\left[\begin{array}{ccc}\cos \psi & -\sin \psi & 0\\ \sin \psi & \cos \psi & 0\\ 0& 0& 1\end{array}\right]\times \left[\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right]\times \left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \varphi & -\sin \varphi \\ 0& \sin \varphi & \cos \theta \end{array}\right]\\ =\left[\begin{array}{ccc}\cos \theta \cos \psi & cos\psi \sin \theta \sin \varphi -\sin \psi \cos \varphi & \sin \varphi \sin \psi +\cos \psi \sin \theta \cos \varphi \\ \sin \psi & cos\theta \cos \psi +\sin \theta \sin \varphi \sin \psi & \sin \psi \sin \varphi \sin \psi -\cos \psi \sin \theta \\ -\sin \theta & \sin \varphi cos\theta & cos\theta cos\varphi \end{array}\right]\end{array}$ (6)

假设四个旋翼螺旋桨在地面坐标系下的升力为F_B，各自产生的升力为 $F_i\left(i=\text{1},\text{2},\text{3},\text{4}\right)$。则在垂直上升的时候可以用如下的式子来表示：

$\begin{array}{l}{F}_B={\left[F_x,F_y,F_z\right]}^{\text{T}}={\left[0,0,U_1\right]}^{\text{T}}\\ U_1=F_1+F_2+F_3+F_4\end{array}$ (7)

通过上述的转换矩阵R可得到在地面坐标系下的升力F_G为：

$F_G=R{F}_B=R{\left[F_x,F_y,F_z\right]}^{\text{T}}$ (8)

因此，可得到机体坐标系三个方向上的线位移加速度为：

$\{\begin{array}{l}\ddot{x}=\frac{U_1\left(\sin \varphi \sin \psi +\cos \psi \sin \theta \cos \varphi \right)}{m}\\ \ddot{y}=\frac{U_1\left(\sin \psi \sin \theta \cos \varphi -\cos \psi \sin \varphi \right)}{m}\\ \ddot{z}=\frac{U_1\cos \varphi \cos \theta }{m}-g\end{array}$ (9)

忽略空气阻力再由物理学关系可知三个角度上加速度为：

$\{\begin{array}{l}\ddot{\varphi }=\frac{U_2}{I_x}=\frac{kl\left(w_4^2-w_2^2\right)}{I_x}\\ \ddot{\theta }=\frac{U_3}{I_y}=\frac{kl\left(w_3^2-w_1^2\right)}{I_x}\\ \ddot{\psi }=\frac{U_4}{I_z}=\frac{kl\left(-w_1^2+w_2^2-w_3^2+w_4^2\right)}{I_z}\end{array}$ (10)

3. 基于神经网络的PID主动减振控制系统

3.1. 控制系统原理

为保证飞行器的稳定飞行，需要对(K_p, K_i, K_d)三个参数进行及时有效的在线整定。基于BP神经网络的PID控制算法，采用改变学习率的方法对BP神经网络算法进行了改进，使得基于此算法的PID控制器的三个参数能够进行在线整定，以此来达到对四旋翼飞行器的自适应主动控制。BP神经网络结构图如图3所示。

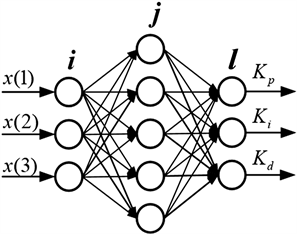
Figure 3. BP Neural Network Structure diagram

图3. BP神经网络结构图

输入层采用增量PID的神经网络，分别为i，j，l层，输入层有三个量，如下所示：

$\begin{array}{l}{x}_1\left(t\right)=e\left(t\right)=r\left(t\right)-y\left(t\right)\\ x_2\left(t\right)=\Delta e\left(t\right)=e\left(t\right)-e\left(t-1\right)\\ x_3\left(t\right)={\Delta }^{2}e\left(t\right)=e\left(t\right)-2e\left(t-1\right)+e\left(t-2\right)\end{array}$ (11)

其中，e(t)表示t时刻的误差，r(t)表示t时刻的目标值，y(t)表示t时刻的实际值。

输出层有一个变量，表示t时刻控制器应当给出的输入控制量的增量。如下所示：

$\Delta u\left(t\right)=k_1{x}_1\left(t\right)+k_2{x}_2\left(t\right)+k_3{x}_3\left(t\right)$ (12)

目标函数表示如下：

$J=\frac{1}{2}{\left(r\left(t+1\right)-y\left(k+1\right)\right)}^2$ (13)

其训练系数的导数如下所示：

$\frac{\partial J}{\partial \omega }=-\lambda \frac{\partial J}{\partial y\left(t+1\right)}\cdot \frac{\partial y\left(t+1\right)}{\partial u\left(t\right)}\cdot \frac{\partial u\left(t\right)}{\partial \omega }$ (14)

权系数的学习算法如下所示：

$\{\begin{array}{l}\Delta {\omega }_{jl}^3\left(t\right)=\alpha \Delta {\omega }_{jl}^3\left(t-1\right)+\eta {\delta }_l^3{O}_j^2\left(t\right)\hfill \\ \begin{array}{l}{\delta }_l^3=e\left(t\right)sgn\left(\frac{\partial y\left(t+1\right)}{\partial u\left(t\right)}\right)\cdot \frac{\partial u\left(t\right)}{\partial O_l^3\left(t\right)}\cdot g^{\prime }\left(ne{t}_l^3\left(t\right)\right)\\ {\delta }_i^2\left(t\right)=f^{\prime }\left(ne{t}_j^2\left(t\right)\right){\displaystyle \underset{l=1}{\overset{3}{\sum }}{\delta }_l^3{\omega }_{jl}^3\left(t\right)}\\ f\left(x\right)=\frac{\exp \left(x\right)-\exp \left(-x\right)}{\exp \left(x\right)+\exp \left(-x\right)}\\ g\left(x\right)=\frac{\exp \left(x\right)}{\exp \left(x\right)+\exp \left(-x\right)}\end{array}\hfill \end{array}$ (15)

NNI辨识器输入层为：

$\{\begin{array}{l}u\left(t\right),u\left(t-1\right),\cdots ,u\left(t-n_u+1\right)\\ y\left(t\right),y\left(t-1\right),\cdots ,y\left(t-n_y+1\right)\end{array}$ (16)

则训练的目标函数为：

$J=\frac{1}{2}{\left(y\left(t+1\right)-\hat{y}\left(k+1\right)\right)}^2$ (17)

3.2. 主动减振控制系统

通过以上算法最终确定了PID控制所需要的最佳三个参数(K_p, K_i, K_d)，将BP神经网络应用于常规的PID控制器中，通过BP神经网络获取飞行器飞行过程中的实时运行状态来不断调整权值系数，再通过不断学习训练，使得输出层神经元的输出状态参数对应PID控制器的三个理想参数，从而在线整定随着外界环境变化而改变的参数。

PID控制采用增量式数字PID控制，表达式如下所示：

$\begin{array}{l}u\left(t\right)=u\left(t-1\right)+\Delta u\left(t\right)\\ u\left(t\right)=u\left(t-1\right)+K_p\left[e\left(t\right)-e\left(t-1\right)\right]+K_{i}e\left(t\right)+K_d\left[e\left(t\right)-2e\left(k-1\right)+e\left(t-2\right)\right]\end{array}$ (18)

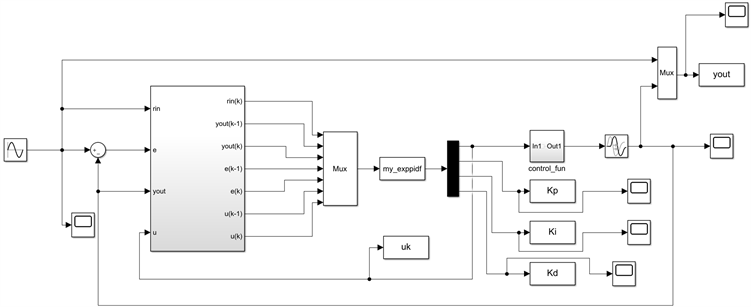
Figure 4. Control scheme of flying height based on BP neural network

图4. 基于BP神经网络的飞行高度的控制方案

将最主要的BP神经网络优化算法写入Simulink里的S函数(my_exppid模块)中，该模块能够在运行的过程中通过BP神经网络算法实时的调整PID的三个关键参数从而实现飞行过程中对飞行器的实时控制。建立基于BP神经网络的飞行高度的控制方案图形化仿真模型如图4所示(由于其余的三个参数分别为偏航角、横滚角、俯仰角这三个参数的变化情况与高度上的变化情况类似，这里就不再赘述)。

本文以空间坐标系内运动的四旋翼飞行器旋翼为研究对象，采用压电传感器检测旋翼中点的弹性变形y(t)，并将其作为控制反馈量；采用偏差e (其中， $e=r-y\left(t\right)$，r为期望值0)及偏差变化率ec作为基于BP神经网络的PID控制器的输入，以满足不同时刻e(t)和ec(t)对PID参数自整定的要求；将控制器的输出u输入至执行机构—压电作动器，压电作动器通过逆压电效应对旋翼施驱动力矩作用，从而抑制旋翼的弹性振动。基于BP神经网络的压电柔性旋翼PID控制结构如图5所示。

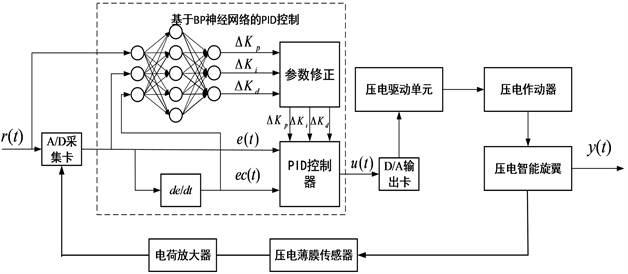
Figure 5. Schematic diagram of PID control structure based on BP neural network

图5. 基于BP神经网络PID控制结构示意图

采用粘贴在柔性旋翼上的压电复合材料作为传感器和作动器，当扰动产生的弹性振动信号有传感器检测到后经过电荷放大器放大处理后，通过数据采集卡将其转换为数字信号输入到计算机，计算机根据基于BP神经网络的PID控制算法对信号进行计算和处理，再经过D/A卡将数字控制量转换为模拟控制信号输出至压电驱动电源处，从而驱动粘贴在柔性旋翼上的压电作动器，由压电作动器产生形变对柔性旋翼形成控制力矩作用，从而达到对柔性旋翼实施振动主动控制的目的。

4. 主动减振仿真结果及讨论

本文以四旋翼飞行器为研究对象进行主动减振仿真试验，其中的传递函数为高度方向上的数学模型为 $G_1\left(u\right)=\cos \varphi \cos \theta u/m-g$ ；俯仰方向为： $G_{\text{2}}\left(u\right)=u/I_y$ ；横滚方向为： $G_{\text{3}}\left(u\right)=u/I_x$ ；偏航方向为： $G_{\text{4}}\left(u\right)=u/I_z$。这里仅对高度方向上的动力学模型进行仿真，其余的三个方向方法类似此处不再赘述。高度控制量经过数学以及动力学计算再对其进行二次积分就能得到实际飞行器的高度。这里设置仿真时间为50 s，预期令该飞行器到达的高度为40 m，接下来分两种情况对该优化后的算法进行分析，分析的具体情况如下所示。

根据图6对比我们可以看出经过BP神经网络算法优化过的控制时间较普通PID控制大约从10秒减到7秒，从而更加快速的达到预期的高度，而且能够在模拟飞行的过程中能够几乎不产生超调量，响应的速度更快更平稳，能够明显的起到在飞行过程中主动减振的目的。

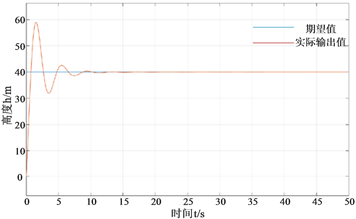(a) 普通PID控制 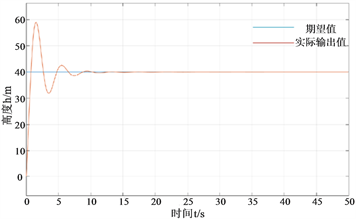(b) 经BP神经网络算法优化后的控制

Figure 6. Two algorithm control height response graphs without disturbance

图6. 无扰动情况下两种算法控制高度响应图

另外，假设在有外界扰动的情况下仿真观察其达到预设高度的到达情况，并且假设在40 m的高度上存在正弦波 $y\left(t\right)=2\times \sin \left(2t\right)+40$ 的小扰动来简单的模拟外界的干扰。此时有扰动情况下两种算法控制高度响应如图7所示。

(a) 普通PID控制 (b) 经BP神经网络算法优化后的控制

Figure 7. Two algorithm control height response graphs with disturbance

图7. 有扰动情况下两种算法控制高度响应图

上述两图的比较下明显的看出飞行器经神经网络算法优化后能够在5s的时候就能够达到基本稳定值完成姿态的调整，能够比普通的PID控制至少减少3秒以上的控制时间。在达到基本稳定之前的控制情况可知，经过算法优化后的模型能够实时调整自己的参数，稳定的达到设定的飞行器40米高度。并且在基本稳定的飞行过程中经过算法优化的控制系统能够较好的预判外界的扰动，从而实时的修改当前的PID参数来减少飞行器飞行过程中的振动情况和快速完成位置与姿态的调整。在稳定之后受到正弦扰动的情况可得出经算法优化后的飞行器飞行过程中实际扰动的振幅要比普通PID控制要小的多，体现出较好的鲁棒性，更够明显的起到在飞行过程中主动减振的目的。

比较在减振控制中加入神经网络算法与不加优化算法普通的PID对旋翼运转过程中的减振效果。这里运用Simulink环境进行仿真，能够比较直观快速的反映出抑振的效果。模拟令旋翼中心的电机产生530 W的功率去驱动飞行器飞行，此时会产生大约23000 (rad/s)的转速，并且分别取扰动频率为10 Hz和20 Hz，其中预设的PID三个关键参数为K_p = 50，K_i = 1，K_d = 1。神经网络自整定PID控制器的参数也预设为一样。则不同频率下两种算法控制旋翼的中点的变形仿真结果如图8所示。

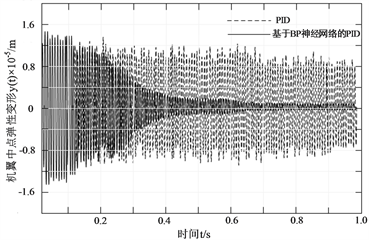(a) 频率为10 HZ且无控制时 (b) 频率为10 HZ时 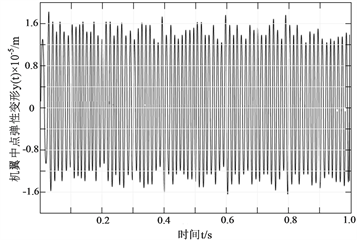(c) 频率为20 HZ且无控制时 (d) 频率为20 HZ时

Figure 8. The y(t) curve diagram of two algorithm control under different frequency

图8. 不同频率下两种算法控制时的y(t)曲线图

由图8仿真结果可以看出飞行器旋翼在正常的运转过程中会产生轻微的形变与振荡，这种形变与振荡在飞行器的飞行过程中无疑会对整体飞行的稳定性产生一定的影响。经过仿真能够得出旋翼的振动频率为20 HZ时最大变形较10 HZ频率下大约高出0.3 × 10⁻⁵ m，且振幅会随着外界扰动频率的增大而增大，这种情况对飞行中的机身稳定是及其不利的。对比后能看出，与普通的PID算法相比较采用BP神经网络算法优化后能够较好的控制叶片飞行过程产生的振动，控制振动效果可相对提高15%这能极大的减小飞行过程中旋翼产生的振荡，能够进一步的提高机体飞行中的稳定性与鲁棒性。

为了验证在考虑实际飞行状态下控制仿真分析，当受到突风扰动的情况下仿真出其恢复正常飞行的振荡响应图，观察如下所示的仿真响应图能得到如下的结论：

图9为考虑实际飞行状态下飞行器恢复正常飞行的振荡响应图，可以清楚的表现出在平稳的飞行过程中在受到突风扰动的飞行情况下，经过基于BP神经网络的PID控制后，虽然在受到突风扰动的一瞬

(a) 沉浮运动的时间历程 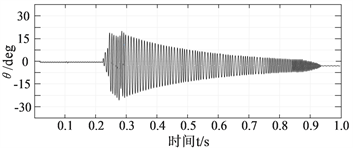(b) 俯仰角运动的时间历程 (c) 偏转角运动的时间历程 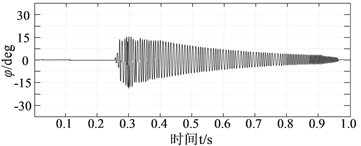(d) 横滚角运动的时间历程

Figure 9. Consider the oscillating response graph under actual flight conditions

图9. 考虑实际飞行状态下振荡响应图

间会产生较大影响，但是控制程序在计算到误差后能够及时参与机身与旋翼的主动减振控制，分析图中响应曲线总体减振效果可达65%左右，且在较短的时间内可快速平稳的达到原本的飞行状态。

5. 结论

本文采取具有良好非线性辨识和控制能力的BP神经网络智能算法的PID控制方法，具有带扰动补偿的反馈控制，在系统参数化、外部干扰和系统内部动力耦合情况下仍具有良好的闭环控制性能。在更短的时间内比常规的PID控制效果提高达15%~25%。考虑实际飞行状态下飞行器恢复正常飞行时，验证了经过基于BP神经网络的PID控制后，控制程序在计算到误差后能够及时参与机身与旋翼的主动减振控制，总体减振效果可达65%左右，且在较短的时间内可快速平稳地达到原本的飞行状态。

NOTES

^*通讯作者。