1. 引言
随着能源的供需关系日趋紧张,提高现有能源的利用率和开发新能源已经成为全球学者关注的热点问题。在工业生产过程中存在大量余热,亟需高效的回收利用,提高能源的利用率。然而高效的余热回收离不开经济、高效的换热器。因此,设计和制造高性能的换热设备成为回收和利用能源的重要手段之一。扭曲管换热器是一种新型高性能换热器,其核心部件为扭曲管,使用扭曲管代替传统的光滑管可以显著地提高传热效率,从而节约金属管材、节省设备费用和降低能耗,具有广泛的应用前景。
目前,学者对扭曲椭圆管的传热和压降性能进行了大量的研究。Bishara [1] 运用数值方法对在扭曲椭圆管内的周期性流动的层流进行了研究,其条件为具有恒定的壁面温边界条件,Re范围为10~1000,Pr为3,对长短轴比为0.3、0.5、0.7,扭曲比为6、9、12的扭曲椭圆管进行了研究,得出结论:与光滑直管相比,扭曲椭圆管具有更加优秀的传热性能。高学农等 [2] 对较高扭曲比的扭曲椭圆管的综合换热性能进行了研究,得到了相关的计算准则式,试验结果显示扭曲椭圆管的传热性能较光滑管有较大提高。Wang [3] 通过实验和数值方法研究了扭曲方形管道和直管道。结论表明扭曲管总是可以获得较好的强化传热效果。在扭曲比和管内流体流态研究方面,Todd [4] 研究了扭曲椭圆管的普遍性问题,他在基于大扭曲比扭曲椭圆管的假设下简化了Navier-Stokes方程,并通过推导得到了流函数的四阶偏微分方程。虽然该分析适用于具有适当边界条件的任何横截面的管道,但其有效性仅仅局限于具有大的扭曲比的扭曲椭圆管。Keun-Shik等 [5] 使用有限差分法对具有较大扭曲比的扭曲椭圆管进行了数值研究,研究了扭曲比和长短轴比对其在确定轴向和圆周速度以及流线型方面的影响。Yang [6] 等通过实验评估了五个扭曲椭圆管的性能,所选取的扭曲椭圆管的长短轴之比为1.49至2.15,扭曲的范围为17.4~32.8,工质的Re范围为600~55,000,覆盖了层流、过渡流和湍流。结果表明,在扭曲管中与过渡流和湍流状态相比,层流状态的液体的传热性能更强。Manglik等 [7] 通过数值工具研究了扭曲矩形管道内层流的传热,Re范围为100~1000,Pr范围为5~100,在恒定壁温和恒定壁热通量的边界条件下他们发现,与参数范围内的等效直管相比,最大传热增强约为14倍。扭曲比会影响管内摩擦系数进而影响传热性能。吴欣慰等 [8] 以水–空气为换热系统、水为管内流体,研究了扁平度、扭距等结构和流动参数对扭曲扁平管传热强化和阻力特性的影响规律,发现扭曲扁平管产生的二次流可以对管内对流传热起到强化作用;减小扭曲比虽然能够提高扭曲扁平管的对流换热系数,但阻力损失增加,不利于提高扭曲管的综合传热性能。Patel等 [9] 通过数值方法研究了扭曲矩形管道在层流下的摩擦系数特征,其中Re范围为100~1000,分析了扭曲比和横截面的长宽比对摩擦系数的影响,得出了对于给定的Re和长宽比,较低的扭曲比会导致较高的摩擦系数的结论。此外,Dzyubenko等 [10] [11] [12] 的研究结果表明,扭曲椭圆管换热器传热性能很大程度上取决于换热器壳体结构,在进口段传热系数较大,充分发展段传热及压降特性沿管长方向呈正弦的周期性变化。刘思宇等 [13] 通过Fluent软件对扭曲管进行了数值模拟分析,得出了扭曲管的压降与温度均以较强规律呈周期性逐渐减少的趋势,并且通过分析得出了其强化传热的主要原因为二次流的产生。张立振等 [14] 通过水–空气和水–水换热模型研究了内螺纹扭曲管换热器的强化传热性能,得出了拟合准则式并且介绍了在工程中扭曲管的实际应用场景。
当前对于扭曲管的研究主要集中在扭曲椭圆管,对扭曲矩形管的研究较少。为了进一步补充扭曲管强化传热的研究,本文通过ANSYS FLUENT V16.0对扭曲矩形管的传热与压降特性开展数值研究,探究了在不同几何参数和不同Re条件下Nu、摩擦系数和换热器综合换热性能随扭曲管结构变化的规律,并分析了扭曲矩形管的强化传热机理,为扭曲矩形管换热器的工程应用、优化设计和科学研究提供参考依据。
2. 数值模型
2.1. 物理模型
本本文所采用的扭曲矩形管为截面周长c = 96 mm的矩形管扭曲而成,管壁材料设置为不锈钢其物理模型如图1所示,几何参数如表1所示。

Figure 1. Physical model of twisted rectangular tube
图1. 扭曲矩形管物理模型示意图

Table 1. System resulting data of standard experiment
表1. 标准试验系统结果数据
2.2. 控制方程
采用Realizable k-ε [15] 模型作为模拟扭曲矩形管管内流动的模型,其控制方程如下所示:
质量守恒方程:
(1)
动量守恒方程(k-ε模型):
(2)
(3)
(4)
式中:
(5)
能量守恒方程:
(6)
2.3 网格划分及边界条件
采用ICEM CFD软件对物理模型进行网格划分,网格类型为结构化六面体网格。通过设置边界层保证计算结果准确,近壁面处采用增强壁面函数,其要求y+ ≈ 1 [16],故通过公式
预估了近壁面尺寸。此外,在导出计算之前,对所有网格进行了平滑处理,以提高网格质量。划分结果如图2所示。
边界条件如图3所示。在扭曲矩形管通道的数值模拟中,流体介质为空气。流体入口基于周期性边界条件,周期类型为Translational。流体入口质量流量为qm = 0.00115992 kg/s,入口温度Tin = 293.15 K。壁面温度设为恒壁温343.15 K,壁面速度设为0。

Figure 3. 3D model of twisted rectangular tube
图3. 扭曲矩形管3D模型
3. 数据处理
将扭曲矩形管的网格导入FLUENT软件中进行数值模拟。当流动状态在单倍换热管扭矩长度上重复时,可认为存在周期性流动条件,且在单倍换热管扭矩长度上流体沿流动方向具有恒定的压降。因此考虑选取合适的建模长度并利用周期性流动的特点进行计算。管内的流体为空气,可以通过改变其入口速度来得到不同的Re来进行实验,Re的计算通过公式(7)表示:
(7)
扭曲矩形管入口速度由公式(8)计算得到
(8)
当管内冷流体入口温度为定值时只需根据不同水力直径改变入口速度及可得到不同的Re,水力直径的计算如公式(9)所示
(9)
局部摩擦因数f的值由公式(10)计算得到
(10)
努塞尔数Nu由公式(11)计算得到
(11)
使用换热管换热性能评价因子η对不同k的扭曲矩形管综合换热性能进行评价,其计算方法如公式(12)所示
(12)
4. 模型计算结果分析
4.1. 数值方法可靠性验证
1) 网格独立性分析
在数值模拟中,网格数目对计算结果有重要影响。因此,为了确保计算结果与网格数无关,进行了严格的网格独立性测试。同一模型不同网格数下的Nu计算值如图4所示。数据表明,当网格数超过约12万时,Nu趋于稳定,这意味着当使用超过12万个网格时,数值模拟的精度足以满足扭曲矩形管的要求。

Figure 4. Grid number of twisted rectangular tube
图4. 扭曲矩形管网格数
2) 模型验证
为保证数值方法的可靠与准确,以Bhadouriya等 [17] 在扭曲矩形管c = 96 mm,k = 1,s = 276 mm,H = 11.5情况下的实验结果作为本文的参考,采用上述几何模型,分别对管内流体在600 ≤ Re ≤ 40000范围内的情况进行数值模拟,并将数值方法所得出的结果与文献中的实验结果进行比对,验证数值方法的可靠性。如图5、图6所示,通过对比发现,实验结果与数值方法计算结果在不同Re下目标特性的数值变化趋势基本相似,故认为数值方法可靠。
4.2. 长宽比对扭曲矩形管性能的影响
管1-1,管1-2,管1-3,管1-4,管1-5为具有相同的扭距但是长宽比不同的扭曲矩形换热管,其中扭距s = 276 mm,长宽比k分别为0.2,0.4,0.6,0.8,1.0,换热管的横截面周长均为96 mm。从换热管的物理模型上看,k越小则换热管将越扁,截面积越小,管内摩擦系数也将增大。在Re为5000、8000、20,000、30,000、40,000的情况下分别对几何参数不同的5根扭曲矩形管进行数值模拟并计算其Nu和f。图7、图8分别为Nu和f随Re变化的情况。结果表明,Nu随着Re的增大而增大,这种变化在Re从7000增加到20,000时特别明显。Nu随着k的增加呈现出先增大后减小的趋势,且在k = 0.4 (管1-2)时达到最大值。以管1-2为例,其在Re由5000增大到40,000的过程中,Nu提高了408.00%。在Re = 40,000时,其与管1-5相比,Nu提高了23.62%。f随着k的增加而减小,当扭曲矩形管的k从0.2提高到1.0时,管内流体的f在计算范围内平均降低了19.88%。

Figure 5. Comparison of Nu between numerical method and relative literature
图5. 数值方法与相关文献Nu的对比

Figure 6. Comparison of friction coefficient between numerical method and relative literature
图6. 数值方法与相关文献中f的对比

Figure 7. Wall Nu number under different Re number at turbulent flow stage
图7. 湍流阶段不同Re下的壁面Nu

Figure 8. Wall friction coefficient under different Re number at turbulent flow stage
图8. 湍流阶段不同Re下的壁面f
湍流状态下扭曲矩形管的综合换热性能如图9所示。k = 0.4的扭曲矩形管在各工况下均具有最好的综合换热性能。从变化趋势上来看,在湍流阶段随着k的增加扭曲矩形管的综合传热性能先升高后降低,且在k = 0.4时达到最好。与几何特征相同的光滑矩形管(管1-5)对比,综合换热性能有一定程度的提高。
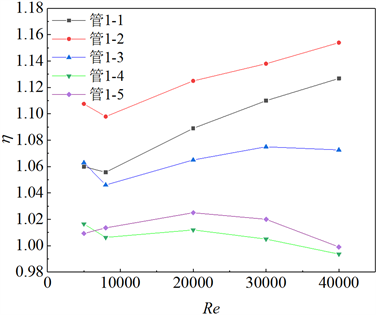
Figure 9. Comprehensive performance of heat exchange tube at turbulent flow stage
图9. 湍流阶段换热管的综合性能
4.3. 扭距对扭曲矩形管性能的影响
管2-1,管2-2,管2-3,管2-4是截面周长c和长宽比k一定,但是扭距s不等的四组扭曲矩形管,其扭距s分别为150 mm、200 mm、250 mm、300 mm。从物理模型上看,扭距s越长,扭曲程度越不明显,摩擦系数越小。在Re为5000、8000、20,000、30,000、40,000的情况下分别对管2-1,管2-2,管2-3,管2-4进行数值模拟并计算其Nu和f。图10、图11分别表示Nu和f随Re变化的情况。结果表明Nu随着s的增加先增大后减小,且在s = 200 mm (管2-2)时达到最大。在计算范围内管2-2的Nu分别较管2-4、管2-1、管2-3平均提高了23.8%、21.27%、12.8%。f随着s的增加先增大后减小且在s = 200 mm (管2-2)时达到最大。在不同Re下对不同扭曲管的f进行对比,发现管2-4、管2-1、管2-3的f在计算范围内较管2-2平均降低了18.17%、16.8%、11.56%。

Figure 10. Wall Nu number under different Re number at turbulent flow stage
图10. 湍流阶段不同Re下的壁面Nu
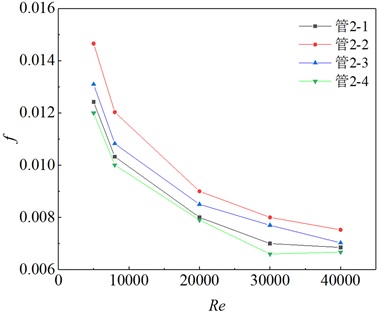
Figure 11. Wall friction coefficient under different Re number at turbulent flow stage
图11. 湍流阶段不同Re下的壁面f
湍流状态下扭曲矩形管的综合换热性能如图12所示,s = 200 mm (管2-2)的扭曲矩形管性能最好。当Re = 8000时管2-2较管2-4的综合性能最多提高15.8%。整体来看扭曲矩形管较相同几何参数的光滑矩形管综合换热性能均有一定程度的提升。但从图中可以看出,随着Re的继续增加,η有减小的趋势,这种趋势在管2-2上尤其明显,推测是由于管2-2内部的f相对较高,影响了流体流速,进而对换热产生不利影响。

Figure 12. Comprehensive performance of heat exchange tube at turbulent flow stage
图12. 湍流阶段换热管的综合性能
4.4. 扭曲矩形管管内强化传热机理分析
图13~15所示分别为管3、管1-5和管1-2的流线图,管内流体以Re = 8000作湍流流动,流线图的范围为单倍换热管扭矩长度s。图中切片面的分布为各换热管等间距横截面的z轴方向的速度分布图。可以发现光滑矩形管内的流动没有二次流 [18] [19] [20] 的出现,而扭曲矩形管的管壁处有明显的二次流出现,且集中于y轴方向的管壁两侧。管1-5中二次流的主要形态为垂直于换热管轴线的上下扰动,管1-2中二次流的主要形态为以扭曲矩形管轴线为中心的螺旋流,同时在换热管的中心区域存在涡流。对比图13和图14可以看出在管1-2中z轴方向的高速区域更加密集,因此二次流在管1-2中更为明显。二次流流态的差别主要是由于各个扭曲矩形管之间的几何参数不同所导致的。从几何特征上来看,扭曲矩形管内的流道为矩形横截面沿换热管轴向扭曲而成,当换热管扭矩s较小,长宽比k较大时,几何特征上扭曲不明显,其对管内流体流动的影响也不明显。而s较大,k较小时,其对管内流体流动的影响显著增加。即

Figure 13. Streamlines and velocity distribution contours in Tube 3
图13. 管3管内流线与速度分布云图

Figure 14. Streamlines and velocity contours in Tube 1-5
图14. 管1-5管内流线与速度分布云图

Figure 15. Streamlines and velocity contours in Tube 1-2
图15. 管1-2管内流线与速度分布云图
扭曲矩形管具有如下特征:首先流道横截面在水平方向上的流动空间逐渐减小,竖直方向的流动空间逐渐增大,之后水平方向上的流动空间逐渐增大,竖直方向的流动空间逐渐减小,该几何特征沿换热管轴向反复出现,从而形成扭曲矩形流道。与管1-5相比,管1-2具有更加强烈的二次流,更好的加强了换热管内液体的横向混合,因而强化了传热效果。
图16(a)~(c)所示分别为管3、管1-5、管1-2的横截面温度分布云图(x = 138 mm)。从图中可以看出扭曲矩形管横截面的温度分布和二次流分布有一定的关联。图16(a)所示为k = 1的光滑管,不存在二次流,温度随流体的流速反向分布,即越靠近管道截面中心处流体流速越高,流体温度越低。而在图16(b)中管1-5由于有二次流的存在,流道横截面处的流体低温区有减小的趋势。而图16(c)管1-2强烈的二次流的作用使得流道横截面的低温区大大缩小,且分割成两端较小区域的低温区,从而进一步扩大了热壁面对冷流体的加热面积,有效提高换热速率。二次流的出现使得该区域的热量交换更为充分,k = 0.4的扭曲矩形管的传热方式由于强烈的二次流的出现由简单的热传导转换为了热对流,达到了很高的传热性能。而光滑管中几乎没有二次流的存在,因此其横截面的温度分布不均匀。

Figure 16. (a) Temperature distribution in cross section of Tube 3; (b) Temperature distribution in cross section of Tube 1-5; (c) Temperature distribution in cross section of Tube 1-2
图16. (a) 管3横截面温度分布图;(b) 管1-5横截面温度分布图;(c) 管1-2横截面温度分布图
5. 结论
通过数值模拟软件对不同几何参数的扭曲矩形管进行了分析,得到了扭曲矩形管管程传热与流动的特点,结论如下:
1) 通过SolidWorks软件建立了物理模型,使用CFD相关软件完成了网格划分和管内流体流动的模拟,得出了壁面平均Nu和f,与前人的实验研究结果进行了比对,确定了数值方法的可靠性。
2) 对得到的不同扭曲矩形管的壁面平均Nu和f进行了对比,发现当600 ≤ Re ≤ 40,000时,随着k的增加综合换热性能先增加后减小,在k = 0.4时达到最大值。随着s的增加,综合换热性能先增加后减少,在s = 200 mm时达到最大值。
3) 对扭曲矩形管管内流线、速度场和温度场进行了分析,结果表明二次流的出现改变了换热管横截面速度场分布,进而影响了流动截面的温度分布,实现了强化传热。
基金项目
“高效节能的换热/反应装备关键技术”产学研合作项目(校企合作)。