不确定环境下的亚式期权定价研究

Research on Asian Option Pricing in Uncertain Environment

摘要: 利率和敲定价格是影响衍生品价格的主要因素，经常会受到经济、政策等不确定因素的影响而产生波动。基于不确定理论，在浮动利率环境下，研究了敲定价格服从不确定指数O-U过程下的亚式期权的定价问题，得到了亚式看涨期权和亚式看跌期权的定价公式，并通过数值模拟分析了不同参数对价格的影响。

Abstract: Interest rate and strike price are the main factors affecting the price of derivatives, which are often fluctuated by uncertain factors such as the economics and policies. Based on the uncertainty theory, the pricing of Asian options whose strike price follows the uncertain exponential Ornstein-Uhlenbeck process under the floating interest rate environment is studied. The pricing formulas of the Asian call option and Asian put option are obtained, while also we analyze the influence of different parameters including the maturity date, such as initial strike price on the price by the numerical simulation.

1. 引言

金融衍生品具有套期保值和规避风险的功能，因此在金融市场上被广泛应用。作为金融衍生品的一种，期权赋予其所有者在交割日期以敲定价格行使权力而不承担义务。自1973年Black和Scholes [1] 给出B-S公式以来，以股票期权为代表的金融衍生品的交易日渐活跃，期权定价也成为了现代金融数学研究的重要问题。

然而金融市场中的股票预期收益率与B-S模型假定不同，为了更好的与现实市场吻合，学者们对B-S模型进行了改进。1976年Merton [2] 提出了跳–扩散模型，给出了该模型下欧式期权的定价公式，1987年Hull和White [3] 研究了随机波动率下的欧式期权的定价问题，1993年Heston [4] 将随机利率下的定价方法应用到了债券和货币期权的定价中。但是，在实证研究中人们发现股票价格并不表现为随机性，投资者信度也影响着市场的变化。2009年Liu [5] 用不确定微分方程来描述股票价格的变化过程，提出了不确定股票模型。在此模型下，Liu和Chen [6] 和Zhang和Liu [7] 分别给出了欧式、美式和几何亚式期权的定价公式，Sun和Su [8] 研究了浮动利率均值回复股票模型下欧式和美式期权的定价问题，Gao、Yang和Fu [9] 讨论了基于不确定指数Ornstein-Uhlenbeck模型下回望期权的定价公式。

在衍生品市场中，亚式期权的交易也较为活跃，它的收益依赖于交割日期标的资产价格的某种平均值，与其他期权相比收益的波动性会小一些。它为投资者提供了一种更为便宜的风险对冲方式，在实践中更容易被接受。近年来许多学者开始研究亚式期权的定价问题。1993年Geman和Yor [10] 通过拉普拉斯变换得到了亚式期权的定价公式。2003年Yang、Huang和Ma [11] 研究了算术平均亚式期权的定价与对冲问题。2011年Hubalek和Sgarra [12] 在带跳的随机波动率模型下研究了几何平均亚式期权的定价。2015年Sun和Chen [13] 得到了一个在不确定股票模型基础上的算术平均亚式期权的定价公式。

目前，针对亚式期权的敲定价格波动性的研究相对较少。考虑到利率和敲定价格也是经济测量的一个重要指标，本文基于不确定理论，假定敲定价格服从不确定指数O-U过程，研究了浮动利率环境下的亚式期权的定价问题。文章第一部分介绍了不确定理论的一些基本知识，第二部分给出了浮动利率环境下的亚式期权的定价公式，第三部分进行了数值模拟，并讨论了价格随不同参数的变化，最后在第四部分对整篇文章总结。

2. 预备知识

引理2.1 (Liu [14] )假设不确定变量 $\xi$ 具有规则的不确定分布 $\Phi$，则 $\text{E}\left(\xi \right)={\displaystyle {\int }_0^1{\Phi }^{-1}\left(\alpha \right)\text{d}\alpha }$。

引理2.2 (Yao和Chen [15] )假设 $X_t$ 、 $X_t^{\alpha }$ 分别是不确定微分方程 $\text{d}{X}_t=f\left(t,X_t\right)\text{d}t+g\left(t,X_t\right)\text{d}{C}_t$ 的解和 $\alpha$ 路径过程，则不确定过程 $X_t$ 的不确定逆分布为 ${\Phi }_s^{-1}\left(\alpha \right)=X_t^{\alpha }$。

引理2.3 (Yao [16] )假设 $X_t$ 、 $X_t^{\alpha }$ 分别是不确定微分方程 $\text{d}{X}_t=f\left(t,X_t\right)\text{d}t+g\left(t,X_t\right)\text{d}{C}_t$ 的解和 $\alpha$ 路径过程，对于 $t>0$ 和严格递增(递减)函数 $J\left(x\right)$，上确界过程 $\underset{0\le s\le t}{\sup }J\left(X_s\right)$ 的 $\alpha$ 路径为

${\Phi }_t^{-1}\left(\alpha \right)=\underset{0\le s\le t}{\sup }J\left(X_s^{\alpha }\right)\left({\Phi }_t^{-1}\left(\alpha \right)=\underset{0\le s\le t}{\sup }J\left(X_s^{1-\alpha }\right)\right)$。

时间积分的 $\alpha$ 路径为

$Z_t^{\alpha }={\displaystyle {\int }_0^{t}J\left(X_s^{\alpha }\right)\text{d}s}\left(Z_t^{\alpha }={\displaystyle {\int }_0^{t}J\left(X_s^{1-\alpha }\right)\text{d}s}\right)$。

引理2.4 (Yao [17] )假设 $X_{1t},X_{2t},\cdots ,X_{nt}$ 是相互独立的不确定过程，如果多元函数 $f\left(x_1,x_2,\cdots ,x_n\right)$ 相对于自变量 $x_1,x_2,\cdots ,x_m$ 严格单调递增，并相对于自变量 $x_{m+1},x_{m+2},\cdots ,x_n$ 严格单调递减，则不确定过程 $X_t=f\left(X_{1t},X_{2t},\cdots ,X_{nt}\right)$ 的 $\alpha$ 路径过程为

$X_t^{\alpha }=f\left(X_{1t}^{\alpha },X_{2t}^{\alpha },\cdots ,X_{mt}^{\alpha },X_{m+1,t}^{1-\alpha },\cdots ,X_{nt}^{1-\alpha }\right)$。

3. 模型

本节我们讨论在浮动利率环境下，敲定价格服从不确定指数O-U过程的亚式期权的定价问题。现实金融市场中，利率和敲定价格会受到经济、政策的影响而产生波动，在此引入浮动利率的不确定指数O-U过程

$\{\begin{array}{l}\text{d}{r}_t=m_1\left(a_1-r_t\right)\text{d}t+{\sigma }_1\sqrt{r_t}\text{d}{C}_{1t}\\ \text{d}{X}_t=\left(m_2-a_2{X}_t\right)\text{d}t+{\sigma }_2\text{d}{C}_{2t}\\ \text{d}{Y}_t=\mu \left(1-c\ln Y_t\right)Y_t\text{d}t+{\sigma }_3{Y}_t\text{d}{C}_{3t}\end{array}$ (1)

其中 $m_1,m_2,a_1,a_2,\mu ,c,{\sigma }_1,{\sigma }_2,{\sigma }_3$ 是正实数， $C_{1t},C_{2t},C_{3t}$ 分别是相互独立的正则Liu过程。

假设亚式期权的标的资产价格、浮动利率和敲定价格的变化过程由(1)给定，则在交割日期为T的算术平均亚式看涨期权价格 $f_c$ 和看跌期权价格 $f_p$ 分别为

$f_c={\rm E}\left(\exp \left(-{\displaystyle {\int }_0^T{r}_t\text{d}t}\right){\left(\frac{1}{T}{\displaystyle {\int }_0^T{X}_t\text{d}t}-Y_T\right)}^{+}\right)$ (2)

$f_p={\rm E}\left(\exp \left(-{\displaystyle {\int }_0^T{r}_t\text{d}t}\right){\left(Y_T-\frac{1}{T}{\displaystyle {\int }_0^T{X}_t\text{d}t}\right)}^{+}\right)$ (3)

定理3.1 模型(1)的算术平均亚式看涨期权和看跌期权的价格分别为

$f_c={\displaystyle {\int }_0^1\exp \left(-{\displaystyle {\int }_0^T{r}_t^{1-\alpha }\text{d}t}\right){\left(\frac{1}{T}{\displaystyle {\int }_0^T{X}_t^{\alpha }\text{d}t}-Y_T^{1-\alpha }\right)}^{+}\text{d}\alpha }$ (4)

$f_p={\displaystyle {\int }_0^1\exp \left(-{\displaystyle {\int }_0^T{r}_t^{1-\alpha }\text{d}t}\right){\left(Y_T^{\alpha }-\frac{1}{T}{\displaystyle {\int }_0^T{X}_t^{1-\alpha }\text{d}t}\right)}^{+}\text{d}\alpha }$ (5)

其中，Jiao [18]，Dai [19] 和Sun [20] 分别给出了浮动利率过程 $r_t$ 和标的资产价格过程 $X_t$ 以及敲定价格 $Y_t$ 的 $\alpha$ 路径过程

$\text{d}{r}_t^{\alpha }=m_1\left(a_1-r_t^{\alpha }\right)\text{d}t+{\sigma }_1\sqrt{r_t^{\alpha }}{\Phi }^{-1}\left(\alpha \right)\text{d}t$

$X_t^{\alpha }=X_0\exp \left(-a_{2}t\right)+\left(\frac{m_2}{a_2}+\frac{{\sigma }_2}{a_2}{\Phi }^{-1}\left(\alpha \right)\right)\left(1-\exp \left(-a_{2}t\right)\right)$

$Y_t^{\alpha }=\exp \left(\exp \left(-\mu ct\right)\ln Y_0+\frac{\left(1-\exp \left(-\mu ct\right)\right)}{c}\left(1\text{+}\frac{{\sigma }_3}{\mu }{\Phi }^{-1}\left(\alpha \right)\right)\right)$

其中

${\Phi }^{-1}\left(\alpha \right)=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }$。

证明：因为 $r_t$， $X_t$， $Y_T$ 是独立的不确定过程，其 $\alpha$ 路径分别由公式(2)，(3)，(4)给出。根据引理2.3可知贴现率 $\exp \left(-{\displaystyle {\int }_0^T{r}_t\text{d}t}\right)$ 的 $\alpha$ 路径为 $\exp \left(-{\displaystyle {\int }_0^T{r}_t^{1-\alpha }\text{d}t}\right)$。

根据引理2.4可知在交割日期投资者各自收益的现值

$\exp \left(-{\displaystyle {\int }_0^T{r}_t\text{d}t}\right){\left(\frac{1}{T}{\displaystyle {\int }_0^T{X}_t\text{d}t}-Y_T\right)}^{+}$

$\exp \left(-{\displaystyle {\int }_0^T{r}_t\text{d}t}\right){\left(Y_T-\frac{1}{T}{\displaystyle {\int }_0^T{X}_t\text{d}t}\right)}^{+}$

的 $\alpha$ 路径分别为

$\exp \left(-{\displaystyle {\int }_0^T{r}_t^{1-\alpha }\text{d}t}\right){\left(\frac{1}{T}{\displaystyle {\int }_0^T{X}_t^{\alpha }\text{d}t}-Y_T^{1-\alpha }\right)}^{+}$

$\exp \left(-{\displaystyle {\int }_0^T{r}_t^{1-\alpha }\text{d}t}\right){\left(Y_T^{\alpha }-\frac{1}{T}{\displaystyle {\int }_0^T{X}_t^{1-\alpha }\text{d}t}\right)}^{+}$。

通过引理2.1和引理2.2，我们得到了

$f_c={\displaystyle {\int }_0^1\exp \left(-{\displaystyle {\int }_0^T{r}_t^{1-\alpha }\text{d}t}\right){\left(\frac{1}{T}{\displaystyle {\int }_0^T{X}_t^{\alpha }\text{d}t}-Y_T^{1-\alpha }\right)}^{+}\text{d}\alpha }$

$f_p={\displaystyle {\int }_0^1\exp \left(-{\displaystyle {\int }_0^T{r}_t^{1-\alpha }\text{d}t}\right){\left(Y_T^{\alpha }-\frac{1}{T}{\displaystyle {\int }_0^T{X}_t^{1-\alpha }\text{d}t}\right)}^{+}\text{d}\alpha }$。

4. 数值模拟

期权定价公式中有很多参数，为了研究价格与这些参数间的关系，我们做了一些数值模拟。通过以下的图(图1和图2)来反映各个参数对价格的影响。在实验中，只有一个参数改变其他参数保持不变。

例1 假定利率的参数分别为： $r_0=0.03,a_1=2,{\sigma }_1=0.04,m_1=0.05$，标的资产价格的参数分别为： $X_0=4,a_2=1,{\sigma }_2=3,m_2=6$，敲定价格的参数分别为： $Y_0=5,c=1,{\sigma }_3=\pi ,\mu =\sqrt{3}$，当 $T=1$ 时，亚式看涨期权的价格为 $f_c=0.7933$。

例2 假定利率的参数分别为： $r_0=0.03,a_1=2,{\sigma }_1=0.04,m_1=0.05$，标的资产价格的参数分别为： $X_{\text{0}}=\text{4,}{a}_2=\text{1,}{\sigma }_2=\text{3,}{m}_2=\text{6}$，敲定价格的参数分别为： $Y_0=3,c=1,{\sigma }_3=\pi ,\mu =\sqrt{3}$，当 $T=1$ 时，亚式看跌期权的价格为 $f_p=4.3775$。

图1给出了不同参数的亚式看涨期权定价公式的曲线图。从(a)可以看出期权价格相对于敲定日期是一个递减函数，期权价格随着敲定日期的延长而降低；(b)反映了期权价格相对于平均股价是一个递增函数，期权价格随着平均股价的增大而上涨；(c)为期权价格相对于平均利率的变化，随着平均利率的增加，期权的价格就会下降，投资者想要高收益，唯一的方式就是降低期权的价格；(d)为初始敲定价格的变化对期权价格的影响，人们总是在价低时买入，所以在增加时，期权价格会降低。

Figure 1. The influence of different parameters on the price of Asian call option

图1. 不同参数对亚式看涨期权价格的影响

图2给出了不同参数的亚式看跌期权定价公式的曲线图。从(a)可以看出期权价格相对于敲定日期是一个递减函数，期权价格随着敲定日期的延长而降低；(b)反映了期权价格相对于平均股价是一个递减函数，期权价格随着平均股价的增大而下跌；(c)为期权价格相对于平均利率的变化，随着平均利率的增加，期权的价格就会下降，投资者想要高收益，唯一的方式就是降低期权的价格；(d)为初始敲定价格的变化对期权价格的影响，人们总是在价低时买入，所以在增加时，期权价格也会随之上升。

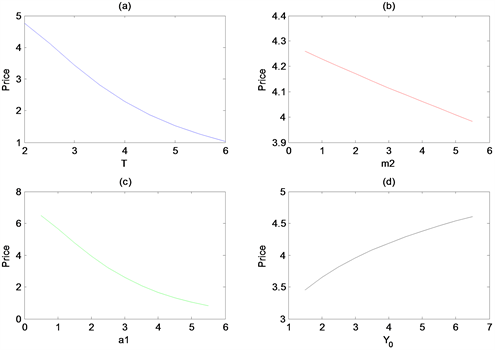
Figure 2. The influence of different parameters on the price of Asian put option

图2. 不同参数对亚式看跌期权价格的影响

5. 结论与展望

本文基于不确定理论，研究了浮动利率环境下的亚式期权的定价问题。考虑到在金融市场中的预期收益率的波动变化，本文选取了不确定指数O-U过程来描述敲定价格的变化情况，首先推导出了亚式看涨期权和亚式看跌期权的定价公式，然后讨论了不同参数对期权价格的一些影响，从数值模拟的图中也可以看出浮动利率以及不确定的敲定价格不但降低了市场风险，更符合实际的金融市场的情况，因此本文的假设更具有现实意义。接下来我们的研究将会围绕在不确定环境下的多资产奇异期权的定价展开。

基金项目

天津市教委科研计划项目(2018KJ113)。

NOTES

^*通讯作者。