基于改进SURF算法的显微图像大范围拼接

Large Scale Microscopic Image Mosaic Based on SURF Algorithm

摘要: 在实现大范围微结构测量时，白光干涉表面测量受限于单个光学视场的大小，不能看到完整的结构。为了获得大范围的视野效果，文中提出基于改进SURF算法对显微图像进行拼接。首先用Harris对图像进行特征点检测，然后对特征点进行描述符计算寻找点对之间的对应点对。再使用RANSAC对误配的点对进行删除，最后使用加权融合的方法来消除拼接缝。实验结果表明，该方法是有效的，可以将多次采集得到多幅图片拼成一幅完整的图片来实现大视野的测量。

Abstract: In large-scale microstructure measurement, the white light interferometric surface measurement is limited by the size of a single optical field of view, and cannot see the complete structure. In order to obtain a wide range of visual field effect, this paper proposes an improved surf algorithm for micro-scopic image mosaic. Firstly, Harris is used to detect the feature points of the image, and then the descriptor of the feature points is calculated to find the corresponding point pairs. Then RANSAC is used to delete the mismatched point pairs, and the weighted fusion method is used to eliminate the seam. The experimental results show that the method is effective, and it can put multiple images collected many times into a complete image to realize the measurement of large field of vision.

1. 绪论

近年来，随着计算机视觉技术的不断发展，在生活中的很多方面都会涉及到图像拼接 [1] [2] 来获得一幅视野较广的图像，广泛地应用在汽车导航 [3]、森林火灾监测 [4]、医学图像分析等多个领域。

图像拼接技术是通过找到相邻两幅图像重合的部分，然后确定两张图像之间的变换关系，最后将两幅图像进行拼接和融合 [5]。该技术能够克服一般成像设备视野受限的弊端，在不改变硬件条件的前提下能够进行大范围测量 [6]。

目前常用的图像拼接算法有直接法和基于特征法这两种。直接法是利用图像间的灰度信息来确定图像之间的变换参数。基于特征法是通过找到图像的特征点，然后对两幅图像的特征点进行匹配来确定图像间的变换参数。目前常用的算法是基于特征法，常见的基于特征的匹配算法有SIFT (Scale Invariant Feature Transform)算法，又称为尺度不变特征变换 [7] [8] [9] 和SURF (Speeded-up Robust Feaures)算法，即快速鲁棒特征算法 [10]。Bay等人 [11] 于2006年提出了SURF算法，它被称为SIFT算法的加速版，该算法采用了积分图像的概念，在多幅图像拼接下具有更好的鲁棒性。特征提取算法目前在机器视觉、人脸识别等领域应用比较广泛 [12]，但是在显微图像的应用上相对来说较少。常用于显微图像拼接是基于SIFT和SURF的征点提取算法，尽管能较大程度上解决上述问题，但是速度慢，而SURF算法在寻找特征点时具有不稳定性，在进行点对匹配时，易造成较多的误匹配，从而对配准结果造成影响 [13] [14]。

基于此，本文提出一种基于改进的SURF算法来进行显微图像大范围拼接。首先利用Harris对图像进行特征点检测，然后再对特征点进行描述符计算寻找点对之间的对应点，使用RANSAC对误配点对进行剔除，最后采用加权融合的方法来消除拼接过程中产生的缝隙。实验结果表明该方法是有效的，可以将多次采集得到多幅图片拼成一幅完整的图片。

2. Harris角点检测

Harris角点检测的思想是在图像中设计一个局部检测窗口，然后让窗口在图像的各个方向上进行微小的滑动，若窗口内区域的灰度发生了较大的变化，那么就认为在窗口内存在角点。如果没有灰度变化或者某一个方向上没有灰度变化，则可认为该窗口不存在角点。对于图像I(x,y)，在点(x,y)处分别平移u和v个单位，可得灰度强度变化的表达式为：

$E_{u,v}\left(x,y\right)={\displaystyle \underset{\left(u,v\right)}{\sum }{W}_{u,v}}{\left[I\left(x+u,y+v\right)-I\left(x,y\right)\right]}^2$ (1)

其中： $E_{u,v}$ 为窗口灰度值； $W_{u,v}$ 为二维高斯窗口的函数。

将 $E_{u,v}\left(x,y\right)$ 化为二次型有

$E_{u,v}\left(x,y\right)=\left(u,v\right)M\left[\begin{array}{c}u\\ v\end{array}\right]$ (2)

式中M称为像素点自相关矩阵。通过计算M，可得到角点响应函数CRF (Corner Response Function)表达式，其中k是常数，取值范围0.04~0.06。

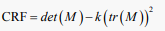(3)

如果某个像素点的角点响应函数值是其周围中的最大值并且超过设置的阈值，则可以将此像素点认为是角点。

3. SURF特征提取算法

SURF算法在保持SIFT算子优良性能的基础上，对兴趣点提取及其特征向量描述进行了改进。与SIFT相比，SURF变得更加稳定且计算效率得到了提高。SURF算法特征提取步骤如下：

1) 极值点检测

SURF算法特征点的提取是基于尺度空间理论，通过寻找图像的局部极值点来确定特征点，一般是局部最暗或者最亮的点。SURF算法检测特征点是通过构造Hessian矩阵来实现的。

2) 特征点定位

首先初步定为特征点，根据Hessian矩阵求出极值后，将其与3维邻域内的26个像素点进行比较，若它比周围26个像素点都大或者都小，则将其保留下来，作为候选特征点。再采用三维线性插值滤掉小于一定阈值的点以及错误定位的关键点，筛选出稳定的特征点。

3) 主方向确定

确定主方向可以保证旋转不变性。以特征点为中心，计算半径为6σ邻域内的点在水平和垂直方向上的Harr小波响应，再根据特征点远近给响应值赋予高斯权重系数，然后将响应值进行累加形成新矢量，选择最长矢量方向作为特征点主方向。

4) 生成特征描述符

以特征点为中心，将坐标轴旋转到主方向，根据特征点的主方向选取边长为20σ的正方形区域，再将该窗口区域划分 $4\times 4$ 的16个子区域，再对每个子区域统计25个像素的水平方向和垂直方向的Harr小波特征。分别得出各个区域相对于主方向而言的水平、垂直方向的Harr小波响应为dx、dy，然后再统计各个方向上的响应及响应的绝对值。

4. RANSAC算法剔除误配点

根据上文所提及的SURF描述方法，我们可以得到图像之间的对应点对，由于两幅图像具有相似性，因此特征点之间也会存在相似性，这会造成对应点对的误匹配。因此本文利用RANSAC算法对误匹配点进行剔除。假定待配准图像的对应点对转换关系可以如下表示：

1) 在特征点的集合中随机抽取4对对应点对，计算其单应性矩阵H。

2) 计算剩余特征对应点在单应性矩阵H变换下的结果，计算出匹配点之间的误差，假如误差小于给定阈值则认为是内点，然后再计算内点的占比率，若占比率大于设定阈值则接受H值。

3) 若内点占比率小于设定阈值，重复1)和2)。

5. 图像融合

完成图像的特征点匹配以后直接拼接图像，在重叠区域会产生裂缝、“鬼影”等变化现象。为了消除产生的裂缝，本文采用加权平均图像融合的方法进行平滑过渡消除这种现象，使图像重叠的中间区域较好地适应左右两边平滑的过渡，实现无缝无损的图像拼接。

6. 实验结果及分析

本次实验利用白光干涉显微镜获取了不同视野下具有重叠的两张照片，利用Matlab平台对基于SURF算法和改进后的SURF算法进行图像匹配，再采用RANSAC算法进行误匹配点剔除。实验结果如图1和图2所示，两者的误配率与效率对比如表1所示。

Figure 1. Before improvement

图1. 改进前

Figure 2. After improvement

图2. 改进后

图1为基于SURF和RANSAC获得的匹配图，在剔除误匹配点之前，初始匹配点为33对，使用RANSAC算法后剩余正确的特征点为22对，匹配时间为3726.57 ms。

图2为基于改进后的SURF和RANSAC获得的匹配图，在剔除误匹配点之前，初始匹配点为8对，使用RANSAC算法后剩余正确的特征点为6对，匹配时间为2469.27 ms。

Table 1. Comparison of mismatch rate and efficiency

表1. 两者误配率与效率对比

由表1的数据可知，改进后的算法在误配率方面相比于之前的SURF算法下降了8.33%；在运行时间上也由3726.566 ms减少到2469.259 ms，相对于改进前提高了33.7%。

为了验证此方法的合理性，在两幅图像匹配的基础上增加实验对象，对三幅具有部分相同的图像进行拼接，待拼接的3幅图像如图3所示，拼接结果如图4所示。结果表明该方法可以完成多幅图的拼接，且在拼接缝合处的效果较好。

Figure 3. Image to be stitched

图3. 待拼接图像

Figure 4. The improved mosaic image

图4. 改进后的拼接图像

7. 结论

本文通过对SURF算法进行研究实现了图像拼接，并基于此提出了一种改进的SURF算法对显微图像进行拼接，一般情况下，由于部分错误特征点的存在，会导致在图像拼接的时候在图像缝合处会有不完全融合情况，改进后的方法降低了匹配点对的误配率以及提高了匹配效率，消除了缝合处不平滑的现象，鲁棒性更强。

NOTES

^*通讯作者。