基于云平台的密文数据离群点检测算法

Outlier Detection Algorithm for Cryptographic Data Based on Cloud Platform

摘要: 将数据和计算外包给云服务器为大规模数据存储和查询处理是一种经济高效的方法。但是由于安全和隐私问题，我们需要在使用云服务器计算过程中保护诸如医疗记录这种敏感数据。一种方法是将加密过的数据外包给云服务器，并让云服务器仅对加密数据执行查询处理，这样云服务器就不会获得有关数据、查询和查询结果的任何知识。在不进行数据云解密的情况下进行加密数据的查询任务是非常具有挑战性的。我们设计的任务是在加密数据条件下云服务器进行安全K近邻(KNN)查询方法进行离群点检测，即用户发送一条加密查询给具有加密数据集的云服务器，并得到该数据是否为离群点的信息。我们首先提出了一个简单方案，并证明该方案并非是完全安全的。之后我们提出了具有更高安全性的安全方案，它能够有效保护用户查询数据、服务器数据集和数据访问模式的机密性。

Abstract: Outsourcing data and computing to cloud servers for large-scale data storage and query processing is an economical and efficient method. However, due to security and privacy issues, we need to protect sensitive data such as medical records in the process of using cloud server computing. One ap-proach is to outsource the encrypted data to a cloud server and have the cloud server perform only query processing on the encrypted data, so that the cloud server does not gain any knowledge of the data, queries, and query results. The query task of encrypting data without data cloud decryption is very challenging. The task we designed is to detect outliers with the cloud server’s secure k-nearest neighbor (KNN) query method under the condition of encrypted data, that is, the user sends an encrypted query to the cloud server with encrypted data set and obtains the information whether the data is an outlier or not. We first propose a simple scheme and prove that the scheme is not completely safe. Then we proposed a security scheme with higher security, which can effectively protect the confidentiality of user query data, server data set and data access mode.

1. 引言

云计算是近年来兴起的计算方式，它具有低成本，高灵活性，高效率的优势，吸引了工业界和许多研究人员的目光，将数据和计算外包给云服务器已经成为了很多组织/企业的选择。通用的云计算模型 [1] [2] 中，用户将自己的数据库放到云服务器上，同时进行数据的查询和管理操作。这样做对用户来说，一方面不用自己建数据库服务器并进行数据运算，降低了数据管理和服务器维护开销，节省了运算开销，减少了运营成本；另一方面，被外包到云服务器上的数据可能存在泄露的危险，数据的查询运算操作也可能会泄露用户隐私，这为云计算带来了安全上的问题。

为保护外包给云服务器的数据不会因为云服务器和黑客攻击而被泄露，一种简单方法是在数据外包给云服务器之前就将数据进行加密处理 [3]。在云服务器的安全查询过程中，需要能够保证：1) 外包给云服务器数据的保密性；2) 用户进行查询数据的保密性；3) 计算过程中隐藏数据访问模式。许多文献提出了与加密数据查询处理相关的技术，例如范围查询 [4] [5] [6]，以及聚合查询 [7] [8] 等等。但是，这些技术对于解决云服务器上加密数据的KNN查询来说要么不适合使用，要么效率不能满足用户的需求。

本文在一种经典的SKNN协议 [9] 基础上，进行修改以提高安全性，使服务器能够在对加密数据进行KNN算法检测离群点的同时，既能够保护数据机密性又能够保护查询数据隐私。在此协议中，数据拥有者一旦将数据加密并提交服务器，就不会再获取后续信息且不参与后续任何计算。特别地，该协议满足以下要求：

1) 数据机密性——数据库数据集T或任何中间结果的内容不应向服务器公开。

2) 查询隐私——输入查询数据Q不应该被泄露给服务器。

3) 正确性——输出应该只透露给客户端用户。并且，除了此信息没有其他信息透露给Bob。

4) 用户上的计算开销尽可能低——将加密的查询记录发送到服务器后，我们的协议在客户端上的计算开销比现有的工作 [1] 低。

5) 隐藏的数据访问模式——对数据的访问模式，例如查询数据Q的k近邻对应的记录，不应该向数据拥有者和服务器公开(以防止任何推理攻击)。

应该强调的是，服务器在我们的协议中看到的中间结果要么是新生成的随机加密，要么是随机数。因此，服务器不知道哪些数据记录对应于查询数据Q的k近邻。此外，在将加密的查询记录发送到服务器之后，用户尽可能涉及最少计算过程使得用户的成本尽可能低。

2. 基础知识

在本文中，隐私安全与协议执行过程中披露的信息量密切相关。有许多方法可以用来定义可披露的信息。为了使数据隐私最大化或者说信息披露最小化，我们采用了之前文献中提出的安全多方计算(SMC)定义，该定义最早是由Yao通过Millionaires问题引入的，并且他们针对该问题开发了一个可证明安全的解决方案。在本文中，我们假设服务器是半诚实的，即诚实且好奇，具体来说，半诚实的服务器使用正确的操作流程遵守协议的规则，但是之后可以自由地使用在协议执行期间得到的中间内容来危害安全性比如数据机密性。一般来说，半诚实模型下的安全协议比恶意对手模型下的安全协议更有效，而文献中提出的实际SMC协议几乎所有都属于半诚实模型下的安全协议。具体来说，我们设置两个半诚实的参与方P1和P2进行交互计算。其中P1具有加密数据库 $E_{pk}\left(T\right)$ 和公钥pk(public key)，P2具有公钥pk和私钥sk (secret key)，我们采用paillier同态加密算法作为加密方式，同时采用一系列安全子协议来构建我们的加密协议。

2.1. Paillier加密

paillier加密基于复合剩余类的难解性，是1999年paillier发明的概率公钥加密系统。该加密算法是一种同态加密，满足加法和数乘同态。其同态性质可描述为：

(1) $E_{pk}\left(a+b\right)\leftarrow E_{pk}\left(a\right)\ast E_{pk}\left(b\right)\mathrm{mod}{N}^2$

(2) $E_{pk}\left(a\ast b\right)\leftarrow E_{pk}{\left(a\right)}^b\mathrm{mod}{N}^2$

2.2. 安全乘法(SM)协议

P1包含 $E_{pk}\left(a\right)$ 、 $E_{pk}\left(b\right)$，且P1和P2不知道a和b的具体数值，经过P1、P2协同计算后将 $E_{pk}\left(a\ast b\right)$ 输出到P1，并且在这个过程中，P1和P2没有得到关于a和b的信息。输出 $E_{pk}\left(a\ast b\right)$ 只有P1知道。安全乘法(SM)协议的基本思想基于以下性质，对于任意给定的 $a,b\in Z_N$，有：

$a\ast b=\left(a+r_a\right)\ast \left(b+r_b\right)-a\ast r_b-b\ast r_a-r_a\ast r_b$

2.3. 安全平方欧几里得距离协议

P1包含 $E_{pk}\left(X\right)$， $E_{pk}\left(Y\right)$，其与P2安全地协同计算向量X和Y之间欧氏距离的平方加密。这里X和Y是m维向量，其中：

(1) $E_{pk}\left(X\right)=\langle E_{pk}\left(X_1\right),\cdots ,E_{pk}\left(X_m\right)\rangle$

(2) $E_{pk}\left(Y\right)=\langle E_{pk}\left(Y_1\right),\cdots ,E_{pk}\left(Y_m\right)\rangle$

最后，输出 $E_{pk}\left({\left|X-Y\right|}^2\right)$ 只有服务器 P1知道。安全的欧几里德距离平方协议SSED的基本思想如下式所示：

${\left|X-Y\right|}^2=\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{\left(x_i-y_i\right)}^2$

2.4. 安全位分解(SBD)协议

P1包含 $E_{pk}\left(z\right)$，其与P2安全地协同计算z的各个比特位的加密，其中 $0\le Z<2^l$。输出 $\left[z\right]=\langle E_{pk}\left(z_1\right),\cdots ,E_{pk}\left(z_l\right)\rangle$ 只有P1知道。这里z₁和z_l分别表示整数z的最高有效位和最低有效位。

2.5. 安全最小(SMIN)协议

P1包含([u]，[v])，服务器 P2包含私钥sk，两个服务器协同安全计算u和v之间小的那一个数的各个比特位的加密，即输出为[min(u,v)]，且该结果只有P1知道。在这个协议中，P1和P2无法得到关于u和v的信息。

2.6. 安全最小n数字(SMINn)协议

P1包含n个加密向量 $\left(\left[d_1\right],\cdots ,\left[d_n\right]\right)$，P2包含私钥sk，这里 $\left[d_i\right]=\langle E_{pk}\left(d_{i,1}\right),\cdots ,E_{pk}\left(d_{i,l}\right)\rangle$，其中 $d_{i,1}$ 和 $d_{i,l}$ 分别为整数d_i的最高和最低有效位，且 $1\le i\le n$。P1和P2协同计算输出 $\left[\min \left(d_1,\cdots ,d_n\right)\right]$。最后， $\left[\min \left(d_1,\cdots ,d_n\right)\right]$ 仅为P1所知晓。并且在SMIN_n协议过程中，P1和P2无法获取有关d_i的信息。

2.7. 安全位或(SBOR)协议

P1包含 $\left(E_{pk}\left(o_1\right),E_{pk}\left(o_2\right)\right)$，其与P2安全地协同计算 $E_{pk}\left(o_1\vee o_2\right)$，其中o₁和o₂是两个二进制数值。输出 $E_{pk}\left(o_1\vee o_2\right)$ 只有P1知道。

3. 方案设计

在本节中，我们首先介绍一个基本的SkNN离群点检测协议，并说明为什么这样一个简单的解决方案不安全。然后，我们讨论第二种方法，一个完全安全的SkNN离群点检测协议。这两个协议都是使用第三节中说明的安全子协议作为构建模块构建的。

我们假设数据拥有者Alice的数据库由n条记录组成，用 $T=\langle t_1,\cdots ,t_n\rangle$ 表示，每条记录有 m个属性，其中t_i,j表示记录t_i的第j个属性值。Alice首先对数据库属性进行Paillier加密，即计算E_pk(t_i,j)，范围为 $1\le i\le n$ 和 $1\le j\le m$，加密后的数据库记为E_pk(T)。我们假设Alice将E_pk(T)以及未来的查询处理服务发送给服务器。同时，我们假设所有的属性值及其欧氏距离都在 $\left[0,{\text{2}}^l\right]$ 范围内。在我们使用的协议中，我们假设存在两个非合谋半诚实的服务提供者，分别用C1和C2表示，它们共同组成一个联合服务器。在此设置下，Alice将加密数据库E_pk(T)发送给服务器C1，将密钥sk发送给服务器C2。我们使用的协议的目标是以高效和安全的方式检索最接近用户查询的k条记录(KNN)并以此为基础进行离群点的检测。简单地说，假设一个授权用户Bob，他想基于服务器C1中的E_pk(T)，确认自己的输入 $Q=\langle q_1,\cdots ,q_n\rangle$ 是否为离群点。Bob最初将他的查询Q(以加密的形式)发送到C1。在此之后，C1和C2使用一组子协议来安全地(以加密的形式)检索输入查询数据Q的k近邻数据集，之后Bob来确认自己的查询数据是否为离群点。我们强调，只有Bob才能获取到Q的k近邻的准确数据，具体协议设置如图1所示。

3.1. 基本安全协议

下面给出了SkNNb协议的主要步骤。Bob首先加密查询数据Q的属性，即计算：

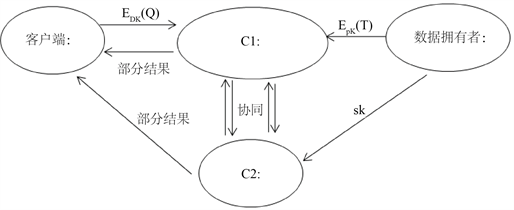
Figure 1. Parties setup of the agreement

图1. 协议各方设置

$E_{pk}\left(Q\right)=\langle E_{pk}\left(q_1\right),\cdots ,E_{pk}\left(q_m\right)\rangle$

然后将其发送到服务器C1。从Bob处接收到E_pk(Q)后，持有输入(E_pk(Q)、E_pk(t_i))的C1和持有私钥sk的C2共同参与到安全欧几里得距离SSED协议中，其中：

$E_{pk}\left(t_i\right)=\langle E_{pk}\left(t_{i,1}\right),\cdots ,E_{pk}\left(t_{i,m}\right)\rangle$

其中i范围为 $1\le i\le n$，这一步的输出为Q与t_i欧氏距离的平方的paillier加密，即 $d_i={\left|Q-t_i\right|}^2$，用E_pk(d_i)表示。如前所述，E_pk(d_i)只有服务器C1知道。我们强调加密向量之间的精确欧氏距离计算是很困难的，因为它涉及到平方根的计算。之后，服务器C1发送 $\left\{\langle 1,E_{pk}\left(d_1\right)\rangle ,\cdots ,\langle n,E_{pk}\left(d_n\right)\rangle \right\}$ 到C2，其中条目 $\langle i,E_{pk}\left(d_i\right)\rangle$ 对应数据记录t_i，i范围为 $1\le i\le n$。之后服务器C2对每个条目进行解密，得到 $d_i=D_{sk}\left(E_{pk}\left(d_i\right)\right)$。然后，C2生成一个索引列表 $\delta =\langle i_1,\cdots ,i_k\rangle$，使得 $\langle d_{i_1},\cdots ,d_{i_k}\rangle$ 为 $\langle d_1,\cdots ,d_n\rangle$ 中K个最短距离的表示。在这之后，C2发送δ到C1。C1收到δ之后，进行如下操作：

1) 选择加密记录 $E_{pk}\left(t_{i_1}\right),\cdots ,E_{pk}\left(t_{i_k}\right)$ 作为查询数据Q的K最近邻记录，并随机化它们的属性。具体而言，C1计算 ${\gamma }_{j,h}=E_{pk}\left(t_{i_j,h}\right)\ast E_{pk}\left(r_{j,h}\right)$， $1\le j\le k$ 且 $1\le h\le m$。这里 $r_{j,h}$ 是Z_N范围内的一个随机数， $t_{i_j,h}$ 表示列h中 $t_{i_j}$ 属性值。然后C1将 ${\gamma }_{j,h}$ 发送到 C2， $r_{j,h}$ 发送给Bob，其中 $1\le j\le k$ 且 $1\le h\le m$。

2) 收到 ${\gamma }_{j,h}$ 之后，服务器C2解密计算 ${{\gamma }^{\prime }}_{j,h}=D_{sk}\left({\gamma }_{j,h}\right)$，并将其发送给Bob。注意，因为C1之前将 ${\gamma }_{j,h}$ 的加密数值随机化，所以 ${{\gamma }^{\prime }}_{j,h}$ 仍然是Z_N范围内的随机数。

3) Bob收到 $r_{j,h}$ 和 ${{\gamma }^{\prime }}_{j,h}$ 之后，使用 ${t^{\prime }}_{j,h}={{\gamma }^{\prime }}_{j,h}-r_{j,h}\mathrm{mod}N$ 来计算查询数据Q的K近邻数据值，其中 $1\le j\le k$ 且 $1\le h\le m$，之后Bob根据得到的K个数值进行离群点的检测，我们采用距离方法顺序进行检测，即从这组数据的第一个开始进行数值欧式距离的判定，一旦存在某一个数值t_i与Q之间的欧式距离大于预设的距离D， $1\le i\le k$，则说明在数据群T中与查询数据Q的欧式距离小于D的点不足k个，判定Q为离群点，否则，Q不是离群点。

3.2. 完全安全协议

上述的SkNNb协议向服务器C1和C2泄露了数据访问模式。也就是说，对于任何给定的查询数据Q，服务器C1和C2都知道哪些数据相当于Q的k近邻记录。然而，在例如医疗数据等隐私敏感的应用条件中，泄露此类信息可能是不可接受的。为此，我们使用了一个完全安全的协议，用SkNN_m表示(其中m代表最大安全)来检索Q的k近邻。

条件：C1持有加密数据库E_pk(T)，随机置换函数π，C2持有私钥sk，客户端Bob提出查询Q1。

客户端Bob将 $E_{pk}\left(Q\right)=\langle E_{pk}\left(q_1\right),\cdots ,E_{pk}\left(q_m\right)\rangle$ 发送至C12.C1和C2：

(1): C1自客户端Bob处接收E_pk(Q)

(2): for i=1 to n:

$E_{pk}\left(d_i\right)=\text{SSED}\left(E_{pk}\left(Q\right),E_{pk}\left(t_i\right)\right)$

$\left[d_i\right]=\langle E_{pk}\left(d_{i,1}\right),\cdots ,E_{pk}\left(d_{i,l}\right)\rangle =\text{SBD}\left(E_{pk}\left(d_i\right)\right)$

for s=1 to k do:

(a): C1和C2:

$\left[d_{\min }\right]={\text{SMIN}}_{\text{n}}\left(\left[d_1\right],\cdots ,\left[d_n\right]\right)$

(b): C1:

$E_{pk}\left(d_{\min }\right)={\displaystyle {\prod }_{\gamma =0}^{l-1}{E}_{pk}{\left(d_{\min ,\gamma +1}\right)}^{2^{l-\gamma -1}}}$

$E_{pk}\left(d_i\right)={\displaystyle {\prod }_{\gamma =0}^{l-1}{E}_{pk}{\left(d_{i,\gamma +1}\right)}^{2^{l-\gamma -1}}},s\ne 1,1\le i\le n$

for i=1 to n:

${\tau }_i=E_{pk}\left(d_{\min }\right)\ast E_{pk}{\left(d_i\right)}^{N-1}$

${{\tau }^{\prime }}_i={\tau }_i^{r_i}=E_{pk}\left(r_i\ast \left(d_{\min }-d_i\right)\right)$

$\beta =\pi \left({\tau }^{\prime }\right)$，将β发送至C2

(c): C2:

自C1处接收β

${{\beta }^{\prime }}_i=D_{sk}\left({\beta }_i\right),1\le i\le n$

for $1\le i\le n$ :

if ${{\beta }^{\prime }}_i=0$ : $U_i=E_{pk}(\; 1\; )$

else $U_i=E_{pk}(\; 0\; )$

将U发送至C1

(d): C1:

自C2处接收U并计算 $V={\pi }^{-1}(\; U\; )$

${V^{\prime }}_{i,j}=\text{SM}\left(V_i,E_{pk}\left(t_{i,j}\right)\right),1\le i\le n,1\le j\le m$

$E_{pk}\left({t^{\prime }}_{i,j}\right)={\displaystyle {\prod }_{i=1}^n{V^{\prime }}_{i,j}},1\le j\le m$

$E_{pk}\left({t^{\prime }}_s\right)=\langle E_{pk}\left({t^{\prime }}_{s,1}\right),\cdots ,E_{pk}\left({t^{\prime }}_{s,m}\right)\rangle$

(e): C1和C2:

$E_{pk}\left(d_{i,\gamma }\right)=\text{SBOR}\left(V_i,E_{pk}\left(d_{i,\gamma }\right)\right),1\le i\le n,1\le \gamma \le l$ 剩余算法步骤与SkNN_b的4~6步相同

我们使用的SkNN_m协议的主要步骤如上述算法所示。首先，Bob发送他的属性加密查询数据Q，即 $E_{pk}\left(Q\right)=\langle E_{pk}\left(q_1\right),\cdots ,E_{pk}\left(q_m\right)\rangle$ 至服务器C1。持有(E_pk(Q)、E_pk(t_i))的C1和持有私钥sk的C2共同参与到安全欧几里得距离SSED协议中。这一步的输出 $E_{pk}\left(d_i\right)=E_{pk}\left({\left|Q-t_i\right|}^2\right)$ 只有C1知道，i范围为 $1\le i\le n$。之后，持有E_pk(d_i)的服务器C1与持有私钥sk的服务器C2使用安全位分解SBD协议安全计算d_i的各个比特位的加密。注意，这一步的输出 $\left[d_i\right]=\langle E_{pk}\left(d_{i,1}\right),\cdots ,E_{pk}\left(d_{i,l}\right)\rangle$ 只有C1知道，其中 $d_{i,1}$ 和 $d_{i,l}$ 分别是d_i的最高有效位和最低有效位。其中 $0\le d_i<2^l$，且 $1\le i\le n$。

之后，服务器C1和C2以迭代的方式计算最接近查询数据Q的k近邻加密记录。更具体地说，他们在第一个迭代中计算 $E_{pk}\left({t^{\prime }}_1\right)$，在第二个迭代中计算 $E_{pk}\left({t^{\prime }}_2\right)$，以此类推。其中 ${t^{\prime }}_s$ 表示距离Q第s近的数据记录，s范围为 $1\le s\le k$，在k次迭代结束时，只有服务器C1知道迭代结果 $\langle E_{pk}\left({t^{\prime }}_1\right),\cdots ,E_{pk}\left({t^{\prime }}_k\right)\rangle$。首先，在第一次迭代中，服务器C1和C2使用安全最小n个数字协议SMIN_n计算 $d_1,\cdots ,d_n$ 中最小值的各个比特位的加密.我们令[d_min]为 $d_1,\cdots ,d_n$ 中最小值，该加密数值只有服务器C1才能知道。现在，服务器C1执行以下操作：

1) 使用下面的公式计算加密数值d_min：

$E_{pk}\left(d_{\min }\right)=\underset{\gamma =0}{\overset{l-1}{{\displaystyle \prod }}}{E}_{pk}{\left(d_{\min ,\gamma +1}\right)}^{2^{l-\gamma -1}}=E_{pk}\left(d_{\min ,1}\ast 2^{l-1}+\cdots +d_{\min ,l}\right)$

其中d_min,1和d_min,l为d_min的最高有效位和最低有效位。

2) 计算加密数据d_min和每一个距离数据d_i的差别，即在 $1\le i\le n$ 范围内计算

${\tau }_i=E_{pk}\left(d_{\min }\right)\ast E_{pk}{\left(d_i\right)}^{N-1}=E_{pk}\left(d_{\min }-d_i\right)$

3) 将 ${\tau }_i$ 随机化，具体表示为 ${{\tau }^{\prime }}_i={\tau }_i^{r_i}=E_{pk}\left(r_i\ast \left(d_{\min }-d_i\right)\right)$，r_i为Z_N范围内的随机数。注意， ${{\tau }^{\prime }}_i$ 是一个加密过的0或一个随机数，其中 $1\le i\le n$。同时，使用随机置换函数π(该函数只有C1知道)将其乱序，得到 $\beta =\pi \left({\tau }^{\prime }\right)$ 并发送到C2。

接到β之后，服务器C2将其解密获得 ${{\beta }^{\prime }}_i=D_{sk}\left({\beta }_i\right)$，其中 $1\le i\le n$。在这之后，C2计算一个长度为n的加密向量U，如果 ${{\beta }^{\prime }}_i=0$ 那么 $U_i=E_{pk}\left(\text{1}\right)$，否则 $U_i=E_{pk}\left(0\right)$。在这里，我们假设β中只有一个元素为零，其他都是随机数。以此类推，U中只有一个元素为加密之后的1，其余元素为加密之后的0。然而，我们强调，如果 ${\beta }^{\prime }$ 中含有不止一个元素为0，那么服务器C2可以随机选择其中一个下标索引i，将E_pk(1)分配给相应的U_i，并将其余的元素设为E_pk(0)。然后，服务器C2把加密向量U发送到服务器C1。收到U之后，C1对其执行逆序，获得 $V={\pi }^{-1}\left(U\right)$。注意，V中只有一个元素为E_pk(1)，其余的都是E_pk(0)。此时，如果 $V_i=E_{pk}\left(\text{1}\right)$，则t_i是离查询数据Q最近的数据记录。然而，服务器C1和C2无法获知V中的哪一项是E_pk(1)。最后，服务器C1计算与Q最接近的数据记录 $E_{pk}\left(t^{\prime }\right)$，并更新距离向量，方法如下：

1) 服务器C1和C2共同参与安全乘法(SM)协议，计算 ${V^{\prime }}_{i,j}=V_i\ast E_{pk}\left(t_{i,j}\right)$，范围为 $1\le i\le n$ 和 $1\le j\le m$。安全乘法SM协议的输出结果 $V^{\prime }$ 只有C1知道。然后，服务器C1通过使用paillier加密的同态属性，计算加密数据记录 $E_{pk}\left({t^{\prime }}_1\right)=\langle E_{pk}\left(t_{1,1}\right),\cdots ,E_{pk}\left(t_{1,m}\right)\rangle$，其中 $E_{pk}\left({t^{\prime }}_{i,j}\right)={\displaystyle {\prod }_{i=1}^n{V^{\prime }}_{i,j}}$，其中 $1\le j\le m$， ${t^{\prime }}_{1,j}$ 为 ${t^{\prime }}_1$ 的第j个属性值。

2) 我们需要注意，最接近查询数据Q的那一个元组应该被排除在后续的计算之外。但是，由于服务器C1不知道与 $E_{pk}\left({t^{\prime }}_1\right)$ 对应的数据记录，因此我们需要强制消除在下一次迭代运算中再次选择该数据记录的可能性。对此，我们让C1将 $E_{pk}\left({t^{\prime }}_1\right)$ 对应的距离更新为最大值，即2l − 1。更具体地说，C1在C2的帮助下，使用安全位或SBOR协议在范围 $1\le i\le n$ 和 $1\le \gamma \le l$ 内更新距离向量 $E_{pk}\left(d_{i,\gamma }\right)=\text{SBOR}\left(V_i,E_{pk}\left(d_{i,\gamma }\right)\right)$。当 $V_i=E_{pk}\left(\text{1}\right)$ 时，相应的距离向量d_i设置为最大值。也就是说，在这种情况下， $\left[d_i\right]=\langle E_{pk}\left(1\right),\cdots ,E_{pk}\left(1\right)\rangle$。但是，当 $V_i=E_{pk}\left(0\right)$ 时，OR操作对d_i没有影响。

重复上述迭代过程k次，直到每次迭代的[d_i]当前对应的记录值均被设置为最大值。但是，由于服务器C1不知道更新的数据对应哪个[d_i]，所以每次迭代都必须使用对应的[d_i]重新计算E_pk(d_i)，i范围为 $1\le i\le n$。在第s次迭代中， $E_{pk}\left({t^{\prime }}_s\right)$ 只有服务器C1知道。

在迭代步骤的末尾，即算法的第3步，C1拥有查询数据Q的k个最近邻的加密记录数据列表 $\langle E_{pk}\left({t^{\prime }}_1\right),\cdots ,E_{pk}\left({t^{\prime }}_k\right)\rangle$。该过程的其余部分类似于SkNNb算法的步骤4到6。简而言之，选择加密记录 $E_{pk}\left(t_{i_1}\right),\cdots ,E_{pk}\left(t_{i_k}\right)$ 作为查询数据Q的K最近邻记录，并随机化它们的属性。具体而言，C1计算 $E_{pk}\left({\gamma }_{j,h}\right)=E_{pk}\left(t_{i_j,h}\right)\ast E_{pk}\left(r_{j,h}\right)$， $1\le j\le k$ 且 $1\le h\le m$。这里 $r_{j,h}$ 是Z_N范围内的一个随机数， $t_{i_j,h}$ 表示列h中 $t_{i_j}$ 属性值。然后C1将 ${\gamma }_{j,h}$ 发送到C2， $r_{j,h}$ 发送给Bob，其中 $1\le j\le k$ 且 $1\le h\le m$。收到 ${\gamma }_{j,h}$ 之后，服务器C2解密计算 ${{\gamma }^{\prime }}_{j,h}=D_{sk}\left({\gamma }_{j,h}\right)$，并将其发送给Bob。注意，因为C1之前将 ${\gamma }_{j,h}$ 的加密数值随机化，所以 ${{\gamma }^{\prime }}_{j,h}$ 仍然是Z_N范围内的随机数。

Bob收到 $r_{j,h}$ 和 ${{\gamma }^{\prime }}_{j,h}$ 之后，使用 ${t^{\prime }}_{j,h}={{\gamma }^{\prime }}_{j,h}-r_{j,h}\mathrm{mod}N$ 来计算查询数据Q的K近邻数据值，其中 $1\le j\le k$ 且 $1\le h\le m$，之后Bob根据得到的K个数值进行离群点的检测，我们采用距离方法顺序进行检测，即从这组数据的第一个开始进行数值欧式距离的判定，一旦存在某一个数值t_i与Q之间的欧式距离大于预设的距离D， $1\le i\le k$，则说明在数据群T中与查询数据Q的欧式距离小于D的点不足k个，判定Q为离群点，否则，Q不是离群点。

4. 实验分析

4.1. 安全性分析

首先，由于查询数据Q经过具有语义安全性的Paillier密码系统加密，Bob的输入查询Q在第四节提出的两种协议中都无法被数据拥有者Alice、服务器C1和C2知晓。

在SkNNb协议中，步骤3(b)的解密操作将欧式距离d_i值泄露给服务器C2。此外，由于C2生成了k近邻索引列表(在算法5步骤3(c)中)并将其发送给C1，因此数据访问模式将被泄露给服务器C1和C2。因此，如果我们不介意di值可以泄露给C2，数据访问模式可以泄露给C1和C2，我们的基本SkNNb协议可以认为是安全的。

另一方面，对SkNNm的安全性分析如下。在算法步骤2中，安全欧几里得距离SSED协议和安全位分解SBD协议的输出是经过加密的，只有服务器C1知道。此外，在安全欧几里得距离SSED协议中所有由服务器C2解密的中间结果在Z_N中都是一致随机的。此外，安全位分解SBD协议是安全的。因此，在算法步骤2中没有泄露任何信息。在每次迭代中，SMINn的输出只有服务器C1知道，而服务器C2不知道任何信息。另外，C1和C2不知道哪个记录对应当前的全局最小值。因此，数据访问模式无法被服务器C1和C2知晓。算法步骤3(c)，β向服务器C2泄露了某个解密的元组满足当前全局最小距离。但是，由于C1发送之前进行了乱序排列，C2无法追溯到对应的数据记录。同时，注意β的解密数据为0或范围Z_N内的随机数进行加密后的数据。同样，由于C2返回给C1的U是加密的向量，C1无法知道哪个加密元组对应当前全局最小距离。因此，在此步骤中，数据访问模式无法被C1知晓。此外，算法步骤3(e)的更新过程不会向服务器C1和C2泄漏任何信息。总之，服务器C1和C2不知道哪个数据记录对应于输出集 $\langle {t^{\prime }}_1,\cdots ,{t^{\prime }}_k\rangle$。

综上所述，很明显，本文使用的SkNNm协议能有效保护数据的机密性、用户输入查询数据的隐私，并隐藏数据访问模式。

4.2. 复杂性分析

SkNNb的计算复杂度受加密、解密和求幂的限制为 $O\left(n\ast m+k\right)$。实际上 $k\ll n\ast m$，因此，受到加密和求幂的限制(假设在Pallier密码系统下加密和解密操作需要相同的时间)SkNNb的计算复杂度为 $O\left(n\ast m\right)$。另一方面，SkNNm的计算复杂度受加密和取幂的限制为 $O\left(n\ast \left(l+m+k\ast l\ast {\log }_{2}n\right)\right)$。

根据密钥大小的不同，我们使用的SkNNm的总体计算成本(高于SkNNb协议)比非加密情况(本文提出的相关工作)高2到3个数量级。这是为了最大化数据保密性所需要付出必要的代价。然而，在客户端，我们使用的协议所用运行时间与非加密情况相当，因为用户只需执行非常少量的操作(受属性数量的限制)，这些操作将在不到一秒的时间内完成。我们的目标是将所有或大部分计算发送给服务器，这样用户就可以使用任何具有存储和有限计算能力的移动设备提出查询。

4.3. 数据对比

我们在一台Windows机器上进行了各种实验。其中我们使用JetBrainsPyCharm作为python编辑器，使用Anaconda作为python第三方库的管理软件，主要使用了python-paillier库进行paillier加密解密，所使用的python版本为3.7。

在数据集选择方面，我们使用了著名的UCI Heart Disease 数据集作为数据库数据T，并选择其中十四个主要属性进行实验。但是由于原数据集数据量较少，且在实际数据集中很难控制参数，我们根据考虑的参数值随机生成合成数据集。利用这些综合数据集，我们可以对不同参数设置下的协议计算成本进行更详细的分析。我们在实验中使用密钥大小不同的Paillier加密技术对这些数据集进行了属性加密，加密后的数据存储在我们的机器上。然后，根据所提议的协议，我们对这个加密数据执行一个随机查询。对于本节的其余部分，我们不讨论数据拥有者Alice的性能，因为它是一次性成本。我们分别评估和分析了SkNNb和SkNNm的性能，然后，我们比较了这两种协议的性能。在我们的实验中，Paillier加密密钥大小S被设置为512位或1024位。

1) SkNNb协议测试

在本小节中，我们通过改变数据记录的数量(n)、属性的数量(m)、最近邻居的数量(k)和加密密钥大小(S)来分析SkNNb协议的计算成本。

首先，通过设置最近邻数量k = 5，密钥大小S = 512，我们评估不同n和m下SkNNb的计算成本。如图2所示，SkNNb的计算成本呈线性增长趋势。例如，当属性数量m = 6时，随着数据记录数量n从2000增加到4000，SkNNb计算时间从44.01秒增加到88.02秒。密钥大小S = 1024时也有类似的趋势，如图3所示。对于任何固定参数，我们发现当S大小增加一倍时，SkNNb的计算时间几乎增加了7倍。

Figure 2. SkNNb trend chart in Case k = 5, S = 512

图2. k = 5，S = 512情况下SkNNb趋势图

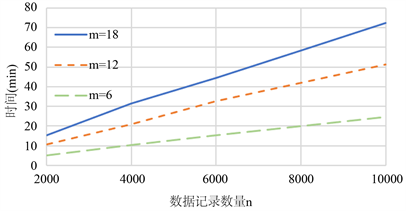
Figure 3. SkNNb Trend Chart in Case k = 5, S = 1024

图3. k = 5，S = 1024情况下SkNNb趋势图

接下来，通过固定设置参数属性数量m = 6和记录数量n = 2000，我们评估了最近邻数量k和密钥大小S变化时SkNNb的运行时间，结果如图4所示。不管密钥大小S是多少，SkNNb不会因最近邻数量k的改变而变化计算时间。这是因为SkNNb大部分的计算成本来自安全欧几里德SSED协议，该协议与最近邻数量k无关。例如，当S = 512位，随着k从5变化到25，SkNNb计算时间从44.01变化到44.11秒。综上所述，可以看出，SkNNb的运行时间主要取决于记录数量n和属性数量m，这进一步证明了我们的复杂性分析是合理的。

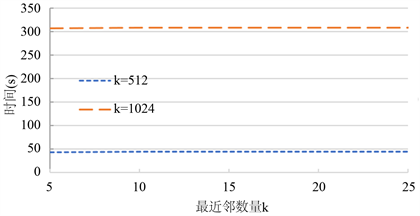
Figure 4. SkNNb Trend Chart in Case m = 6, n = 2000

图4. m = 6，n = 2000情况下SkNNb趋势图

2) SkNNm协议测试

我们还评估了最近邻数量k、属性值大小(二进制位数)l和密钥大小S值变化时SkNNm的计算成本。在本小节中，我们固定属性数量m = 6且数据数量n = 2000。我们发现SkNNm的运行时间也几乎呈线性增长。

当密钥大小S = 512位时，变化最近邻数量K和属性二进制位数l，产生的SkNNm计算量如图5所示。由图5可知，当l = 6时，随着k从5变为25，SkNNm的运行时间从11.91变为55.58分钟。同样，对于l = 12，SkNNm的运行时间随着k从5变为25，由20.56分钟变为97.83分钟。无论哪种情况，SkNNm的计算成本几乎与k和l呈线性增长。

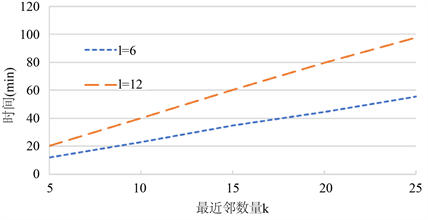
Figure 5. SkNNm trend chart in Case n = 2000, S = 512

图5. n = 2000，S = 512情况下SkNNm趋势图

在S = 1024时也观察到类似的趋势，如图6所示。特别地，对于任何给定的固定参数，我们发现当S增加一倍时，SkNNm的计算成本几乎增加了7倍。例如，当k = 10时，SkNNm分别花费22.83分钟和157.16分钟生成S = 512和1024位下查询数据Q的10个最近邻。此外，当k = 5时，我们发现在SkNNm中约有69.7%的成本是由于安全最小n个数字协议SMINn在SkNNm中启动了k次。同时，当k值从5增加到25时，SMINn引起的成本从69.7%增加到至少75%。

Figure 6. SkNNm trend chart in Case n = 2000, S = 1024

图6. n = 2000，S = 1024情况下SkNNm趋势图

此外，通过设置记录数量n = 2000，属性数量m = 6，属性大小l = 6和密钥位数S = 512，我们比较两个协议在不同的K值下的运行时间，如图7所示，SkNNb的运行时间一直约为0.75分钟，因为它几乎与k不相关。然而，当我们把K从5增加到25，SkNNm的运行时间从11.91分钟变化到55.58分钟。

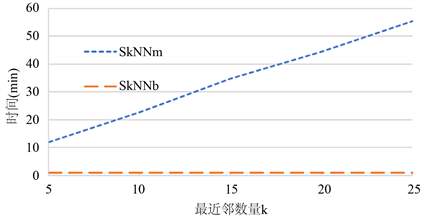
Figure 7. Trend comparison chart between SkNNm and SkNNb

图7. SkNNm与SkNNb趋势对比图

从以上结果可以看出，SkNNm的计算成本明显高于SkNNb。但是，我们强调SkNNm比SkNNb更安全。在SkNNb中，安全欧几里得距离SSED协议最耗费时间，而在SkNNm中，则是安全最小n个数字SMINn协议。另外，需要注意的是，Bob的计算成本主要是由于其输入查询记录的加密和最终离群点的计算造成的。例如，对于m = 6，当K分别为512位和1024位时，Bob的计算成本分别为10和37毫秒。这进一步表明，从终端用户的角度来看，我们的协议非常有效。

5. 总结

k近邻是离群点检测常用的查询方法之一。在将加密数据存储在数据库环境中，对加密数据的安全查询处理变得很有挑战性。现有的基于加密数据的SkNN技术是不安全的。在本文中，我们使用了两种新的基于加密数据的SkNN协议进行离群点的检测。作为基本解决方案的第一种协议向服务器泄漏了一些信息。但是，我们使用的第二个协议是完全安全的，能够保护数据、用户输入查询的机密性，并隐藏数据访问模式。然而，第二种协议比基本协议计算成本更高。此外，我们还评估了协议在不同参数设置下的性能。

关于在客户端进行离群点最终检测问题，因为服务器C1和C2得到K近邻数据之后分别用随机数扰动再汇总到客户端。直接得出欧式距离后与固定距离D进行比较，在不将数据泄露给服务器C2的情况下是不可能进行的，所以我们还没有研究出如何直接在服务器上安全地进行离群点检测。其实我们可以在获取到Q的k近邻数据后将其加密并二次发送至服务器进行离群点检测，但是存在一个问题，就是解密之后才能继续判断是否为离群点，但这又会让C2得知离群点检测的信息。关于进一步降低客户端的计算成本，我们留待以后进行研究。

基金项目

文章研究成果由国家电网有限公司科技项目“面向数据中心的数据共享分发安全关键技术研究及应用”(项目编号Grand No. 5700-202090192A-0-0-00)支持。