1. 引言
瑕疵识别一直都是图像领域一个重要的分支,而布匹良品检验是纺织行业生产和质量管理的重要环节,但一直以来布匹良品和瑕疵品都是依靠人眼检验区分的。人工检验存在速度慢、劳动强度大,易受主观因素影响,缺乏一致性等问题,严重降低了纺织生产流程的自动化程度。因此,研究布匹良品自动检验方法对于实际生产有着重要意义。
目前对于布匹良品检验的方法,主要是针对布匹瑕疵检测。而布匹瑕疵图案的检测方法主要为:基于频域特征提取的方法 [1] [2];基于空间域的灰度共生矩阵法 [3];基于模型算法的自回归模型 [4];基于布匹瑕疵纹理结构的算法 [5],混合算法 [6] [7] [8] [9] 等。上述算法仅适用于背景纹理较为简单的布匹图像瑕疵检测,对于复杂背景的图像,特征提取效果较差,且泛化性能较差。
随着深度学习的兴起,深度卷积神经网络(Deep Convolutional Neural Network)因不需要人工设计特征提取算法、模型泛化能力强等优点在计算机视觉中的应用越来越广泛。文献 [10] 构建了一个具有多层结构的CNN网络并结合softmax来解决色织物缺陷分类的问题;文献 [11] 分别采用了AlexNet [12] 和GoogleNet [13] 对织物的花型进行分类;文献 [14] 验证了CNN网络能够有效的区分钢材表面的缺陷。这些研究表明深度卷积神经网络在图像分类中具有很好的适用性,克服了传统方法的不足,但上述方法的分类准确率仍有较大的提升空间。
本文基于ResNet50 [15] 深度卷积网络,分别在数据处理、网络结构和损失函数上进行改进,并构建了基于滑动窗口的分类模型,应用于布匹瑕疵检测,大幅提升了模型对正常布匹和瑕疵布匹的区分能力。
2. 基于ResNet50网络的布匹良品检验算法
2.1. 网络结构
ResNet的主要优点是可以利用更深层次的网络解决训练误差随网络层数的增加而增大的问题。为了解决该问题,ResNet对传统的网络结构进行了调整,其关键结构是将基本的网络单元增加了一个恒等的快捷连接。如图1所示,H(x)为理想映射,F(x)为残差映射,H(x) = F(x) + x。通过将拟合目标函数H(x)转变为拟合残差函数F(x),把输出变为拟合和输入的叠加,使得网络对输出H(x)与输入x之间的微小波动更加敏感。
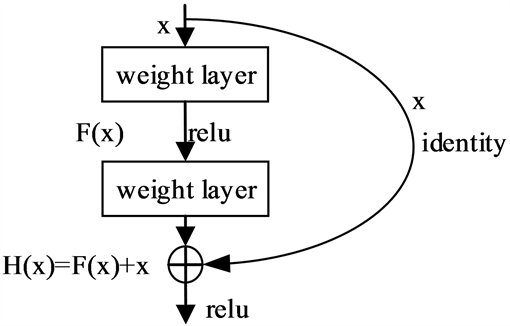
Figure 1. Added residual network unit of shortcut connection
图1. 添加了快捷连接的残差网络单元
综合考虑了网络深度以及计算复杂度的问题,本文选取了ResNet50作为分类网络。ResNet50是残差网络的典型代表之一,与ResNet101和ResNet152相比,有适中的网络深度和计算量,同时能够保持较高的分类准确度。
ResNet50的网络结构图如图2所示,它有两个基本构建块,一个是Identity Block,另一个是Conv Block。Identity Block不改变输入特征图的尺寸和通道数,可以连续串联,其结构如图3所示。Conv Block中存在卷积核大小为1 × 1,步长为2的卷积层,缩小了特征图的尺寸,起到下采样的作用。此外,快捷连接上的特征图与主支路上的特征图在模块末尾进行融合,经过Conv Block的特征图通道数会翻倍,其结构如图4所示。

Figure 2. ResNet50 network structure
图2. ResNet50网络结构

Figure 3. Identity Block structure diagram
图3. Identity Block结构图
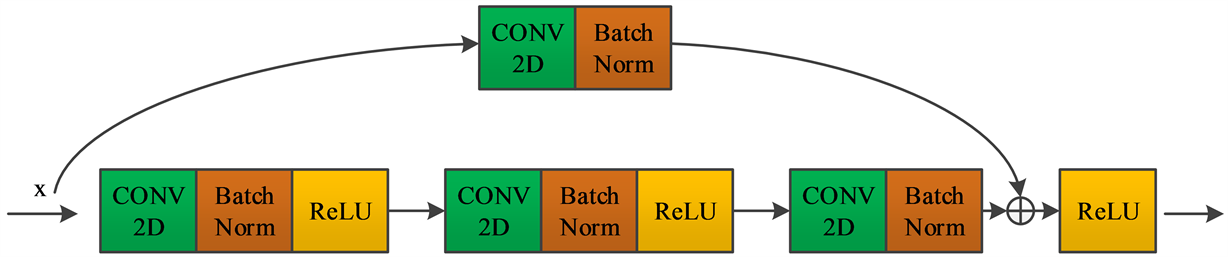
Figure 4. Conv Block structure diagram
图4. Conv Block结构图
ResNet50网络的默认输入为224×224像素的图像,图像经过conv1~conv5的处理后得到大小为7×7的特征图,再经过全局平均池化层和全连接层,最终通过softmax输出对应每个类别的概率。
2.2. 图片数据预处理
本文使用的布匹数据集来自天池大数据竞赛——雪浪AI制造挑战赛,该数据集的图片可分为正常布匹和含瑕疵布匹两大类,其中瑕疵类别中包含了毛边、擦洞、边扎洞、缺经、缺玮等47种缺陷数据。训练集中正常布匹数量为1316张,含瑕疵的布匹数量为706张,测试集中包含正常与瑕疵布匹图片共662张。为了方便在训练中监督模型的收敛效果,本文从训练集中随机抽取10%的图片作为验证集。图片的分辨率统一为2560 × 1920,对于包含瑕疵的图片,数据集提供了记录瑕疵位置的标注文件,如图5所示,图5(a)和图5(b)是正常的布匹,图5(c)含毛边,图5(d)含擦洞,均为瑕疵图像。
 (a) 正常布匹
(a) 正常布匹  (b) 正常布匹
(b) 正常布匹  (c) 毛边
(c) 毛边  (d) 擦洞
(d) 擦洞
Figure 5. Cloth image data set
图5. 布匹图像数据集
2.2.1. 基于像素区域关系重采样的图片缩放
网络输入图片的像素大小直接影响网络的参数计算量以及特征的学习效果,本文所用的数据集的图片像素均为2560 × 1920。同VGGNet和GoogleNet等网络一样,ResNet50网络的默认图片输入尺寸为224 × 224,若将图片按原图大小直接输入网络,则会造成网络计算复杂度过大,难以训练。所以需要对原数据集的图片进行缩放再放入网络训练。
常见的图片缩放方法为双线性插值法,通过实验发现,采用该方法对原图进行缩放,生成的图片会有波纹状干扰,如图6(a)所示。为了解决此问题,本文采用了基于像素区域关系重采样的图片缩放法,其计算式如下:
(1)
其中
,
是原图上的位置信息,
,
是目标图像的位置信息。生成的图片如图6(b)所示,可见相对于双线性插值法,基于像素区域关系重采样的图片缩放法有效地减少了波纹状干扰。
 (a) 双线性插值
(a) 双线性插值  (b) 基于像素重采样
(b) 基于像素重采样
Figure 6. Comparison chart of different zoom methods
图6. 不同缩放方式的对比图
2.2.2. 数据增强
数据增强的作用是扩大有效的训练样本,防止因训练数据太少导致模型学习不充分,训练所得结果无法达到预期 [16]。
本文首先采用的数据增强方法是对图像进行随机上下翻转和镜像翻转以及90˚旋转生成新的图像。布匹瑕疵不但具有不同的形状,而且瑕疵的角度具有一定随机性。通过原图的随机翻转及旋转可以一定程度上消除样本多样性不足的问题,增强效果如图7所示。其中图7(a)为原图,图7(b)~(d)分别为上下翻转,镜像翻转以及随机旋转90˚的效果图。
此外,还对图片进行了水平和竖直方向上的平移以及随机改变图片亮度并添加高斯噪声来进一步增强训练集,图8(a)是改变了图片亮度及添加了高斯噪声的效果图,图8(b)和图8(c)分别是在水平方向平移和竖直方向平移之后的效果图。
2.3. 基于滑动窗口的检测方法
除了将原图直接缩放到固定尺寸进行训练和测试外,为了更加关注图像中的细节,借鉴了滑动窗口检测 [17] 的思想构建了新的分类模型,具体做法如下:
 (a) 原图
(a) 原图  (b) 上下翻转
(b) 上下翻转  (c) 镜像翻转
(c) 镜像翻转  (d) 旋转90˚
(d) 旋转90˚
Figure 7. Data enhancement effect chart (1)
图7. 数据增强效果图(1)
 (a) 改变亮度添加高斯噪声
(a) 改变亮度添加高斯噪声  (b) 水平方向平移
(b) 水平方向平移  (c) 竖直方向平移
(c) 竖直方向平移
Figure 8. Data enhancement effect chart (2)
图8. 数据增强效果图(2)
① 对于训练集中的正常布匹图片,采用512 × 512的滑动窗口,步长为256进行重采样,获得小图。对于包含瑕疵的图片,若采用同样的方式进行采样,由于大多数缺陷在原图中的面积占比较小,采样得到的大部分图片都不包含瑕疵且存在部分图片仅包含瑕疵边缘。本文计算了重采样得到的小图中瑕疵部分面积与原图瑕疵面积的比值θ。在本文的实验中:当θ大于0.1时,将该小图归为含瑕疵样本,其余图片均归于正常样本。
(2)
为了保持合理的正负样本比例,本文从正常样本中随机抽取5%的样本量(与原数据集正负样本比例保持接近)作为最终训练集中的正常布匹样本,得到的数据仍使用ResNet50网络进行训练。
② 对于①中得到的训练集,本文仍采用2.2中的数据增强方式对训练集进行数据增强。
③ 对于测试集,采用同样的滑窗重采样方式得到小图,对小图分别预测该图为含瑕疵布匹类别的概率,再将排名前三的概率求均值作为该图为含瑕疵布匹类别的概率。
基于滑动窗口的检测方法示意图如图9所示,其中网络输入是由滑动窗口重采样得到的子图,通过网络可以预测每张子图所属的类别。
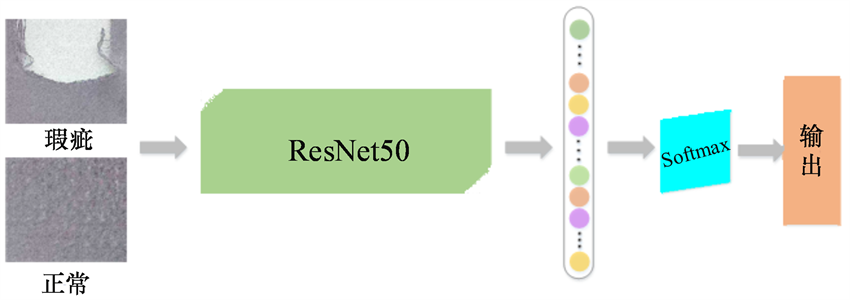
Figure 9. Schematic diagram of sliding window detection
图9. 滑窗检测示意图
2.4. 损失函数的优化
交叉熵 [18] 是分类任务中常用的损失函数,对于二分类模型它的损失函数如下:
(3)
其中
是模型对于实例为正类的预测概率,
。使用交叉熵损失函数,对于正样本而言,输出的预测概率越大,则损失越小。对于负样本而言,输出的概率越小则损失越小。当训练样本中存在较多简单的样本,则训练过程会在这些简单样本的迭代上消耗较多时间,且对于那些较难分类的样本,很难进行优化。
本文使用的布匹数据集的瑕疵类别的样本中,存在着一些如破洞、扎洞等较为明显的瑕疵,但同样也存在着如含油脂、织稀等较难区分的样本,为了改善上述的情况,本文借鉴了Focal Loss [19] 的思想,重新定义了损失函数:
(4)
,与标准的交叉熵损失函数相比,当预测概率较大时,新的损失函数的损失值将会减小,而当预测概率较小时,损失值将会增大,使得训练过程更加关注那些较难区分的样本。
2.5. 训练与测试
数据集的训练与测试的流程图如图10所示。
按照图10(a)的过程对训练集进行训练,每训练完一个epoch,对验证集进行测试,记录在测试集上的准确率并保存模型。训练完后,选取在验证集上表现最好的模型按照图10(b)的步骤对图片进行测试,记录每张图对应于含瑕疵布匹类别的概率,最终计算AUC以及F1分数等评价指标。
3. 实验结果及分析
3.1. 实验设置
按2.2中的处理方法将数据集分别处理成224 × 224、800 × 600两种不同输入尺寸。此部分数据集均包含训练集1822张、验证集200张和测试集662张。再通过2.3所述的滑动窗口重采样的方法得到的512 × 512大小的数据集。共有训练集6484张,验证集922张,采用带动量因子(momentum)的小批量(mini-batch)随机梯度下降法(stochastic gradient descent, SGD) [20] 并加载ImageNet [21] 预训练模型对网络进行训练。对于不同输入尺寸大小的图片,网络初始学习率、每个训练批次图片数量以及训练轮次的设置如表1所示。
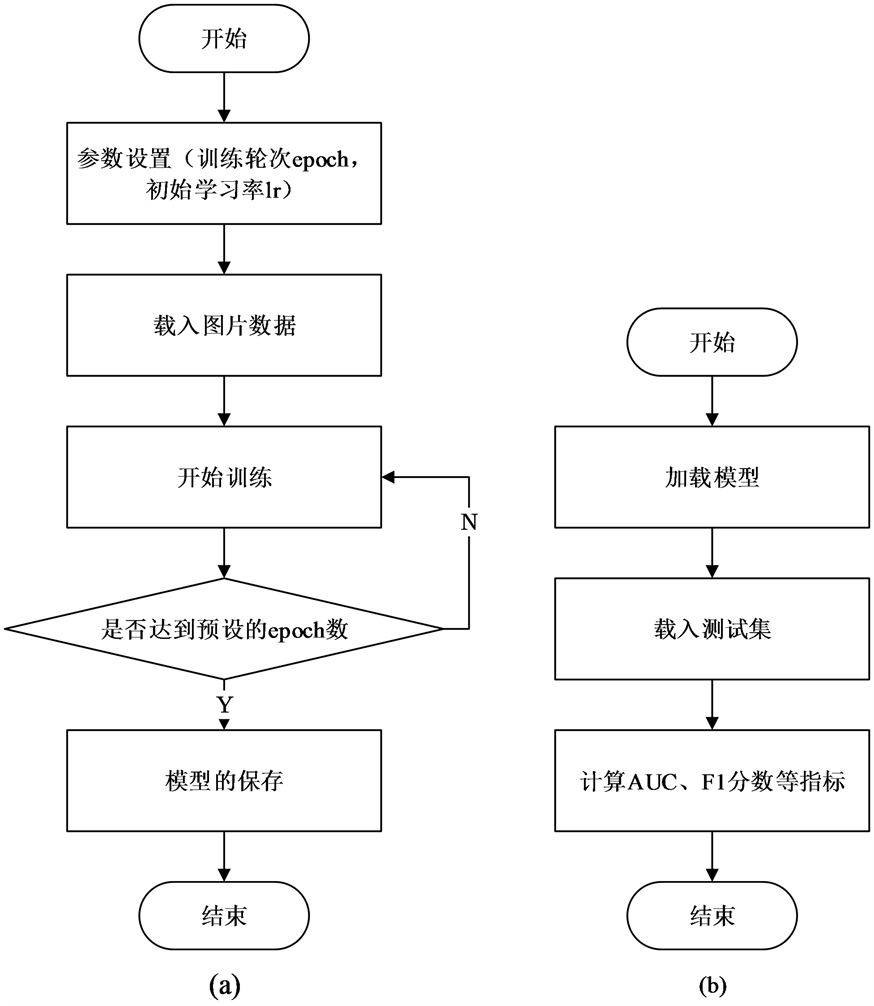
Figure 10. Flow chart of training and testing process
图10. 训练及测试过程的流程图

Table 1. Training parameter settings
表1. 训练参数设置
对于表1中前两组数据训练所得模型,测试集分别缩放至同样的尺寸再进行测试。对于滑动窗口检测模型,测试集同训练集一样,每张2560 × 1920像素大小的原图由512 × 512大小的窗口用256步长采样得到小图。对小图分别进行测试,求他们为瑕疵类别的概率,再将概率大小前三的图片的预测概率求均值作为原图为瑕疵类别的概率。
本文所有实验均是在keras深度学习框架下进行的,电脑的操作系统为ubuntu16.04,CPU为因特尔I7处理器,32 G运行内存,GPU为TITAN X (12 GB),使用GPU加速计算。
3.2. 结果分析
3.2.1. 评价指标
1) AUC (Area Under the Curve)
ROC (Receiver Operating Characteristic)曲线是用于评价分类模型性能的常用标准之一。它的横坐标为伪正类率FPR (False Positive Rate),即预测为正但实际为负的样本占所有负例样本的比例,纵坐标为真正类率TPR,(True Positive Rate),即与预测为正且实际为正的样本占所有正样本的比例,FPR和TPR的计算公式如下:
(5)
其中TP为被模型预测为正类的正类样本数;TN为被模型预测为负类的负样本数;FP为被模型预测为负类的正类样本数;FN为被模型预测为正类的负样本数。
对于二分类模型,通过分类得到每个实例属于正类的概率P,设定阈值θ,当P > θ时,该实例为正类,否则为负类,对应可以计算出一组(FPR, TPR),从小到大调整阈值,将得到的点连接即得到ROC曲线。AUC为ROC曲线下的面积,单独看ROC曲线难以评判两个分类器的好坏,AUC的值越大,表明模型的泛化性能更好,可以通过比较AUC数值的大小来衡量分类模型的性能好坏。
2) F1-Score
F1分数(F1 Score),同样是衡量分类模型精度的重要指标,它同时兼顾了分类模型的精准率(Precision)和召回率(Recall),可以看做是二者的加权平均,它的计算公式如下:
(6)
其中精准率表示被判定为正类的样本中实际为正类的比重,召回率表示被判定为正类且实际为正类的样本占总的正样本的比重,二者的计算公式如下:
(7)
3.2.2. 不同网络结构及输入图片尺寸的比较
对于缩放至224 × 224、800 × 600两种不同尺寸的数据集,按照表1中的参数设置分别用GoogleNet、VGG16和ResNet50网络进行训练、测试和比较。图11是三个网络在不同尺寸数据集上测试结果的ROC
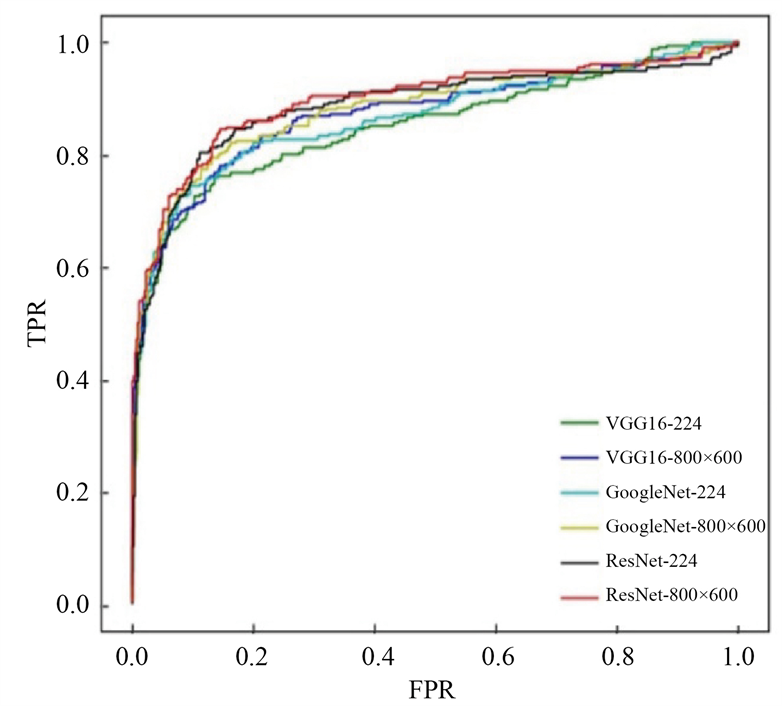
Figure 11. The model corresponds to the ROC curve of different size inputs
图11. 模型对应于不同尺寸输入的ROC曲线
曲线,表2记录了图10中每条曲线的AUC值,即曲线下方所围成的面积,表3记录了不同模型对应的F1分数。从表2和表3可以看出,ResNet50训练所得的模型在测试集上的AUC值以及F1分数明显优于GoogleNet和VGG16,通过对比224 × 224与800 × 600两种不同图片输入尺寸所得的模型的测试结果,可以发现,增大输人图片的尺寸,减少原图在缩放过程中的特征丢失,有利于网络分类性能的提升。

Table 2. AUC test results of different networks for different input sizes
表2. 不同网络对于不同输入尺寸的AUC测试结果

Table 3. F1 scores of different networks for different input sizes
表3. 不同网络对于不同输入尺寸的F1分数
3.2.3. loss优化的检验
上述实验均采用交叉熵作为损失函数,此部分实验将损失函数替换成了2.4中重新定义的损失函数,图片输入尺寸大小统一设置为800 × 600,分别对三个网络重新进行训练和测试,测试结果的AUC值及F1分数如表4和表5所示。
改进的损失函数使得训练中更加关注那些较难学习的样本,从表3可以看出,使用改进的损失函数后,三个网络模型在AUC和F1分数上的表现均有上升,证明增大困难样本在训练过程中的损失,能够提高模型的分类性能。

Table 4. Comparison of AUC of model test obtained from different loss function training
表4. 不同损失函数训练所得模型测试的AUC比较

Table 5. Comparison of F1 scores of models trained with different loss functions
表5. 不同损失函数训练所得模型的F1分数比较
3.2.4. 滑窗检测方法的测试结果
基于上述实验结果,本文将滑窗检测方法的采样块大小设置为512 × 512像素,网络为ResNet50,训练过程采用2.4中重新定义的损失函数,实验结果如表6所示:

Table 6. Test results of sliding window model
表6. 滑动窗口模型的测试结果
滑窗检测方法的测试结果AUC高达0.935同时F1分数可以达到0.841。两个评价指标均是所有模型当中最高的。可见利用原图缩放后所得图片进行训练,会因为原图的部分特征丢失,影响模型对图像特征的学习效果,而基于滑窗检测的模型,更能关注图像中的细节,所以拥有更好的分类性能。
3.2.5. 模型分类速率的比较
网络的参数量、深度以及输入图片尺寸的大小等因素均会影响模型最终的分类速率,本文对不同网络结构、不同输入尺寸以及基于滑窗检测的模型分别进行了分类速率评估,表7是模型在测试集上处理图片的平均时间。结果显示模型的分类速率随着输入图片的尺寸增大而下降,此外增加滑窗操作后,模型的分类速率也会有一定程度上的下降。

Table 7. The average time for different models to process a picture (unit: second)
表7. 不同模型处理一张图片的平均时间(单位:秒)
4. 结论
本文提出一种基于深度卷积神经网络的图像瑕疵识别方法,并应用于布匹良品检验环境中。本文基于ResNet网络,在网络输入、数据增强以及损失函数上进行了优化和改进。此外,提出的基于滑窗的瑕疵检测方法,更加关注图像中的细节,训练所得模型在测试集上的AUC达到了0.935的同时F1分数可以达到0.841,相较于原ResNet训练所得模型有较大提升。尽管增加滑窗的操作降低了模型的分类速率,但在分类准确率上有较大幅度的提升,布匹质检的环境对模型的实时性要求并不高,相较于速度而言,模型对缺陷的识别能力更为重要。基于滑窗检测的模型是本文提出的性能最好的模型。
布匹的瑕疵类别多种多样,后期的工作将在利用更细致的样本库,针对不同的瑕疵进行精准检测和识别。
基金项目
本项目获家自然科学基金(No. 61971168)和浙江省自然科学基金(No. LY18F030009)支持。
NOTES
*通讯作者。