1. 引言
在实际应用中,许多测量或调查的数据往往是带有偏度的,如医学、空气污染、金融、经济等。在科学研究中,这类数据一般假定为对数正态模型。对数正态分布在许多应用中是普遍而有效的,对数正态分布的参数估计是一个非常有趣的问题。关于对数正态分布参数统计推断的研究很多,如均值、多个对数正态分布的公共均值、公共变异系数等。例如,Weerahandi [1]、Tsui和Weerahandi [2] 介绍了广义变量法,包括假设检验问题的广义置信区间和广义p-值的构造,成为应用于对数正态分布的有力工具;Tian和Wu [3],Behboodian和Jafari [4] 用广义变量方法对几个对数正态总体的公共均值进行了推断;W. H. Wu和H. N. Hsieh [5] 构造了关于delta对数正态分布均值的广义置信区间;K. Krishnamoorthy,T. Mathew [6] 利用广义p-值和广义置信区间对对数正态分布的均值进行统计推断;J. Hannig,H. Iyer和P. Patterson [7] 介绍了基准广义置信区间;Thangjai、Niwitpong和Niwitpong [8] 建立了公共变异系数的区间估计;Zhou和Tu [9] 用似然法和bootstrap法建立了对数正态分布均值比的区间估计。近几十年来,贝叶斯方法在统计推断中得到了广泛的应用,尤其是对数正态分布。K. Aruna Rao和J. G. D’Cunha [10] 构建了对数正态分布中位数的贝叶斯推断;Maneerat、Niwitpong和Niwitpong [11] 构建了对数正态分布的单均值和两均值之差的贝叶斯置信区间;Harvey和Merwe [12] 构建了对数正态分布和二元对数正态分布的均值和方差的贝叶斯置信区间;Zeller [13] 讨论了均值对数正态分布的贝叶斯分析与非贝叶斯分析的比较。
然而,带有偏度的对数正态分布通常具有极低的可度量性,这对中位数的影响要小于均值。因此,在这种情况下,中位数是一个比均值更有意义的集中趋势的度量。Rao和D’Cunha [8] 利用四个先验密度提出了贝叶斯后验估计和贝叶斯可信区间。Zeller [13] 讨论了对数正态分布中值的贝叶斯估计。就我们所知,关于两个独立对数正态分布的中位数之比统计推断的研究论文很少。本文利用似然法、广义变量法和贝叶斯方法对两个对数正态总体中位数之比进行了统计推断。此外,我们根据覆盖率、平均长度和相对偏度评估所构建的置信区间的性能。各节内容如下:
第二节主要介绍了对数正态模型,以及构造最大似然估计和置信区间的方法。第三节提出了基于两种不同的广义枢轴量的广义置信区间和广义p-值的假设检验。在第四节中,我们用Diffuse先验和独立Jeffreys先验和模拟算法给出了贝叶斯后验点估计、可信区间和后验概率比检验。第五节给出了衡量置信区间优良的数值模拟,包括讨论和结果。在第六节中,我们将用一个真实的数据来说明所提出的推断方法。最后的结束语在第七节给出。
2. 似然方法
考虑两个独立的对数正态分布,其参数为
。令
是来自两个独立总体的随机样本,则有:
其概率密度函数为:
其中
。
根据数理统计的知识我们不难得到:
,参数
的极大似然估计(MLE)为:
对于两个独立对数正态分布,其中位数之比为:
这里的
就是本文关心的统计量。由极大似然估计的不变性,我们运用“插入法(Plug-in)”可以得到参数
的一个点估计为:
这里
分别是
的观测值。下面我们考虑参数
的置信区间的构造,由渐进正态理论和Delta方法,当样本量趋于无穷时,估计
具有渐进正态性,其渐进均值和方差为:
由于参数
是未知的,我们同样可以利用“插入法”,以
来代替未知参数,即
的观测值。
因此,给定显著性水平
,则参数
的
双边渐进置信区间为:
其中,
为标准正态分布的
分位数。
3. 广义枢轴量方法
假设
是来自一个总体的随机样本,该总体取决于参数
,其中
是我们感兴趣的参数而
是讨厌参数。广义枢轴量
是随机样本Y,观测值y,和参数
的函数,其具有以下性质:
·
的分布与未知参数无关;
· 广义枢轴量的观测值
不取决于讨厌参数
。
则参数
的广义枢轴量可以定义为:
其中
定义为:
其中
相互独立,为:
不难说明,
满足上述两条性质,因此,参数
的
双边广义置信区间为:
其中,
与
分别为
的
分位数和
分位数。
除了上面的广义枢轴量的构造方式之外,我们给出另外一种构造方式:
在这种情况下,
定义为:
其中,
和
分别为
和
的独立复制。则参数
的
双边广义置信区间为:
其中,
与
分别为
的
分位数和
分位数。
基于广义枢轴量而构建广义置信区间可以总结为如下算法:
· 给定
。
· 从
至m循环
生成随机变量
并计算
;
生成随机变量
并计算
;
· 结束循环;
· 计算
与
为
上下界,
与
为
上下界。
下面我们考虑假设检验问题:
接下来,我们给出广义检验统计量和广义p-值的概念。广义检验统计量
是样本Y,观测值y,和参数
的函数,满足如下性质:
· 给定观测值y,
的分布与讨厌参数无关;
· 对于
,
的观测值与未知参数无关;
· 给定
,
是关于
单调的。
如果
关于
是随机增长的,则广义p-值定义为
;反之,如果
关于
是随机下降的,则广义p-值定义为
。
为了记号的方便,我们令
,那么假设检验就变成了
下面我们给出广义检验统计量的具体形式:
不难验证,按照上述定义的广义检验统计量满足以上的三个条件,且这时该检验的广义p-值可以定义为:
如果广义p-值低于一个显著性水平
,则拒绝原假设,反之,拒绝备择假设。对于一个复杂的分布,直接计算广义p-值是一项十分复杂的工作,因此我们通常借助模拟的方式来估计广义p-值。
下面给出计算广义p-值的算法流程:
· 给定
。
· 从
至M循环
生成随机变量
以及
;
计算
;
比较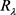 和
的大小,如果
小于
,记“1”,否则记“0”;
和
的大小,如果
小于
,记“1”,否则记“0”;
· 结束循环
· 广义p-值
的估计为:
4. 贝叶斯方法
本节我们将利用贝叶斯方法给出待估参数
的点估计、可信区间和后验概率比检验。我们主要考虑两种不同的先验:
· Diffuse先验:
· 独立Jeffreys先验:
根据贝叶斯公式,基于上述两种先验的后验密度分别为:
同样地,
我们不难发现,后验分布其实是四个密度函数的乘积,其中
以及
那么,待估参数
的贝叶斯后验估计为:
下面我们通过最高后验密度(HPD)的方法构建贝叶斯可信区间,因此,关于
和
的
的双边贝叶斯可信区间为:
其中,
和
是
关于后验密度
的最短最高后验密度区间的下极限,同样,
和
是上极限。贝叶斯后验估计的计算本质上是积分的计算,同样是一件复杂的工作,因此,我们需要通过模拟的方法进行估计以及构建可信区间。
下面我们给出构建贝叶斯可信区间和后验估计的算法流程:
· 给定
。
· 从
至m循环
关于后验
生成
以及
;
关于后验
生成
以及
;
关于后验
计算
;
关于后验
计算
;
· 结束循环
· 贝叶斯后验密度估计为:
· 计算
以及
。
我们继续考虑假设检验
则参数
的后验概率比为:
如果后验概率比
,则接受原假设,如果后验概率比
,则拒绝原假设,如果
,则我们需要更多的后验信息。
接下来给出计算后验概率比的算法流程:
· 给定
。
· 从
至m循环
关于后验
生成
以及
;
关于后验
生成
以及
;
关于后验
计算
;
关于后验
计算
;
比较
和
大小,如果
,令
,否则
。
· 结束循环
· 贝叶斯后验概率比为:
,关于
,
5. 数值模拟
在本节中,我们利用RStudio来评估所构建的五种置信区间(
和
)的表现。我们提出以下的指标来衡量区间的表现:
· 覆盖率(CP):模拟的置信区间覆盖住
的比例;
· 平均长度(AL):模拟置信区间的平均长度;
· 相对偏度(RB):
其中,“lower error rate”为
低于区间下极限的次数的比例,同样“upper error rate”可类似定义。在模拟学习中,我们选择显著性水平
。对于任何参数配置,我们分别从两个独立对数正态总体中生成5000组随机样本来构建95%置信区间。我们选取样本量大小
分布为
。所有模拟结果均被记录在表1、表2和表3中。表1中的参数配置为
以及
,表2的参数配置为
以及
,表3的参数配置为
以及
。

Table 1. Simulation results of Coverage Probability, Average Length and Relative Bias of CIs where (Sigma1, Sigma2) = (0.1, 0.1)
表1.覆盖率、平均长度和相对偏度的模拟结果

Table 2. Simulation results of Coverage Probability, Average Length and Relative Bias of CIs where (Sigma1, Sigma2) = (0.1, 0.3)
表2. 覆盖率、平均长度和相对偏度的模拟结果

Table 3. Simulation results of Coverage Probability, Average Length and Relative Bias of CIs where (Sigma1, Sigma2) = (0.3, 0.3)
表3. 覆盖率、平均长度和相对偏度的模拟结果
模拟结果分析
基于表1、表2和表3:
· 若考虑“覆盖率”,基于两种广义枢轴量以及Diffuse先验所构造的置信区间要更优于其他两种方法的置信区间。对于小样本和中等样本,基于Diffuse先验的贝叶斯可信区间表现更好,然而,两种广义置信区间更适用于大样本。
· 若考虑“平均长度”,基于似然方法构造的置信区间要明显优于其他几种,但无论参数的配置是怎样的,通常伴随着较低的覆盖率。
· 若考虑“覆盖率”和“平均长度”,两种广义枢轴量构造的广义置信区间的表现几乎一致,但在
的情况下,第二种广义置信区间的“相对偏度”较大,但当
时,其“相对偏度”会较低。
· 关于两种贝叶斯方法,基于Diffuse先验的贝叶斯可信区间在“覆盖率”之下是表现更好的,但通常区间长度会更长,因此,若要得到更“短”的置信区间,基于独立Jeffreys先验的贝叶斯可信区间是更适合的。
· 对于相对较大的
或者
相差较大的情形,我们构造的置信区间通常伴随着明显较宽的区间长度,这种情形在
时尤为明显。
总而言之,对于小样本或中等样本,基于Diffuse先验的贝叶斯方法值得被推荐,对于大样本,两种广义枢轴量构造的置信区间更适合。但若想要得到较短的区间,也就是在考虑“平均长度”的情形下,似然方法以及基于独立Jeffreys先验的贝叶斯方法表现更好。
6. 实例分析
大气细颗粒物(PM2.5)是指直径小于或等于2.5微米、可以长时间悬浮在空气中的颗粒物。其主要化学成分为碳氢化合物、氮氧化物、硫氧化物、金属离子化合物、卤素化合物。它可以作为反应床,进行各种反应,将初级污染物转化为次级污染物。它们来源广泛,随着时间的推移,空间分布也各不相同。由于其粒径小,重量轻,长期漂浮,可被吸入肺部,对人体健康造成极大危害。PM2.5主要来自汽车尾气、燃煤和工业废气,在交通发达、人口众多的发达城市尤为严重。
在本例子中,我们研究了北京和广州的PM2.5质量浓度,这两个城市在中国都是比较发达的城市,交通流量大,但就经验而言,位于南海沿岸的广州,空气质量总体上比北京好。因此我们会用提出的方法比较两个区域测量的中位数之比。我们在2020年7月10日至2020年10月25日每隔4天早上8:00(北京时间)同步记录PM2.5质量浓度实时数据,数据来源:http://www.young-0.com/airquality/。
我们记录到的数据如下:
· 北京PM2.5 (ug/m3):91, 83, 66, 122, 38, 168, 68, 72, 89, 115, 38, 145, 152, 30, 53, 30, 25, 8, 38, 76, 164, 17, 38, 200, 21, 61, 59;
广州PM2.5 (ug/m3):46, 46, 13, 17, 30, 25, 25, 66, 30, 53, 8, 24, 34, 53, 153, 21, 17, 25, 8, 38, 21, 70, 38, 81, 51, 42, 66。
图1显示了两个城市的原始数据和经过对数变换之后数据的QQ图(其中,左上和左下两张图是原始数据,右上和右下是经过对数变换的)。这些图表明PM2.5质量浓度的分布是正偏态的,但经对数变换后的图像近似对称,这直观地说明了对数变换后的数据具有正态性。经对数变换后两市的正态性Shapiro-Wilk检验的p-值分别为0.5283和0.8618,两市原始数据的p-值分别为0.02777和0.0002015。因此,有充分的证据表明北京和广州的PM2.5质量浓度分别服从对数正态分布。

Figure 1. QQ-plots of PM2.5 mass concentration in Beijing and Guangzhou
图1. 北京和广州两市PM2.5浓度的QQ图
在表4中,我们给出了PM2.5质量浓度数据对数变换后的汇总统计。在表5中,我们根据提出的方法给出了
的95%双边置信区间。基于似然法
的点估计分别为1.8057、基于贝叶斯后验密度
的点估计分别为1.8533、1.8475。现在考虑假设检验问题,令
,我们分别给出广义p-值0.0038,以及基于后验密度
的后验概率比0.004419446和0.002004008。因此,我们需要拒绝原假设,接受备择假设。这一结果可以解释为2020年7月10日至10月25日广州PM2.5质量浓度中值低于北京。这也意味着这段时间广州的空气质量比北京好,这与事实相符。

Table 4. The summary statistics of log-transformed data both in Beijing and Guangzhou
表4. PM2.5质量浓度数据对数变换后的统计量汇总


Table 5. The 95% two-sided confidence intervals for theta
表5. 待估参数
的95%的双边置信区间
7. 结束语
本文的主要任务是构造基于似然、广义枢轴量和贝叶斯方法的置信区间。通过数值模拟,我们发现基于两种广义枢轴量和贝叶斯后验密度
的置信区间在覆盖率方面较好,而基于似然的置信区间由于渐近理论在大样本中表现较好。从广义枢轴量的性质来看,它的构造不是唯一的,由此得出广义置信区间的构造也不是唯一的。实际上,目前我们还不知道哪一种方法是构造广义置信区间的最优方法。与贝叶斯方法类似,如何选择先验也是一个永恒的话题。因此,这需要进一步的研究。
致谢
非常感谢为本文做出贡献的老师、同学们还有朋友们,以及感谢为本文提供数据的网站:http://www.young-0.com/airquality/。