1. 引言
GeoGebra是数学教授Markus Hohenwarter于2002年创建的动态教学软件,并通过开源的方式不断地更新、完善和推广。GeoGebra功能强大、操作简单、资源丰富,能够进行动态交互,可脱机、可在线,能跨平台使用,且占用空间极小,在欧美等国家已获数十项相关领域的大奖 [1]。GeoGebra在动态显示、直观性、精确性方面表现都非常优秀。GeoGebra 5.0 beta版本新增加的3D功能,可以制作空间立体图形,而且支持几何变换,可以多角度观察立体。将其与高等数学教学相结合,可收到事半功倍的效果。
高等数学作为一门高等学校工科类专业的基础课,对其他专业课的学习起着重要的作用,课程知识点多,难度大,理论抽象。计算旋转体的体积在高等数学课程中具有重要地位,其基本思想是利用微元法将问题转化为定积分的计算。但是由于空间结构复杂,学生很难透彻理解公式背后的意义。在本文中,通过两个具体实例,应用GeoGebra软件,直观、立体地展示旋转体形成过程,让学生充分认识旋转体体积公式的本质。通过动态演示,更深刻地体会“线动成面,面动成体”的微积分思想,有效地理解和记忆公式。旋转体 [2] 就是由一个平面图形绕这平面内一条直线旋转一周而成的立体,这条直线叫做旋转轴。
2. 基于“切片法”,利用GeoGebra动态演示旋转体的形成过程
2.1. 实例1的计算方法
实例1:由
,
,
所围成的图形分别绕x轴及y轴旋转,计算所得两个旋转体的体积。
按照文献 [2] 中280页的描述,按照如下公式计算体积
绕x轴旋转,
(1)
绕y轴旋转,
(2)
2.2. 关于实例1的GeoGebra软件操作步骤
1) 分别打开绘图区、3D绘图区、代数区。
2) 在绘图区建立滑动条t,类型为角度,范围0度到360度;建立滑动条m,n,类型为数值,范围0到1,增量为0.01。
3) 指令栏分别输入:
f(x) = 如果(0 ≤ x ≤ 4, sqrt(4 - x)),A = (0, 2),B = (4, 0),O = (0, 0),a = 线段(A, O),b = 线段(O, B),
c: 0 ≤ x ≤ 4 Ù 0 ≤ y ≤ sqrt(4 - x)。
在对象c的属性中将样式的线径调整为0,以便去掉不需要的线条。
说明:建立平面图形区域。
4) 指令栏分别输入:
d = 曲面(a, t, x轴),e = 曲面(f, t, x轴),g = 旋转(f, t, x轴)。
说明:平面图形区域绕x轴旋转。
5) 指令兰分别输入:
C = 描点(b, m),D = (x(C), sqrt(4 - x(C))),E = 描点(f, n),F = (x(E), 0),h = 线段(C, D),i = 线段(E, F),
f_1 = 如果(x(F) ≤ x ≤ x(C), sqrt(4 - x)),j:x(E) ≤ x ≤ x(D) Ù 0 ≤ y ≤ sqrt(4 - x)。
在对象j的属性中将样式的线径调整为0,以便去掉不需要的线条。
说明:建立参数可调节的微元平面图形区域。
6) 指令栏分别输入:
k = 曲面(f_1, t, x轴),p = 曲面(线段(F, E), t, x轴),q = 曲面(线段(D, C), t, x轴)。
说明:微元区域平面图形区域绕x轴旋转。
7) 指令栏分别输入:
r = 曲面(b, t, y轴),s = 曲面(f, t, y轴)。
说明:平面图形区域绕y轴旋转。
8) 在绘图区建立“复选框”,在下拉列表中选取“曲面e”,标题改为“外部曲面”。
在绘图区建立“复选框”,在下拉列表中选取“曲面r”和“曲面s”,标题改为“绕y轴旋转”。
说明:通过复选框可以选择观察旋转体不同部分。
2.3. 操作说明
调整图形中所有对象的颜色、透明度,可以增强整个动态图形的显示效果。通过滑动条t演示旋转体的生成过程,通过鼠标在3D绘图区拖动,可以从各个视角观察图形。通过滑动条m,n演示微元的变化。
图1——微元图形区域绕x轴旋转形成的立体;图2——所围平面区域绕x轴旋转的过程;图3——所围平面区域绕y轴旋转形成的立体;图4——代数区和绘图区。
2.4. 切片法的微积分思想
通过动态演示体会“线动成面、面动成体”的微积分思想。理解旋转体体积公式(1)、公式(2)中的被积函数就是由一条直线段绕旋转轴旋转而得到的切片的面积。在积分变量的取值范围内,这个平面切片在垂直于旋转轴方向连续变动就生成了旋转体,这些无限个面累加形成体积的过程就是积分。
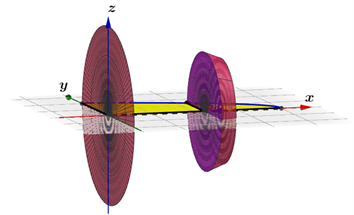
Figure 1. In Example 1, the solid formed by rotation of the element graph region about the x axis
图1. 实例1中微元图形区域绕x轴旋转形成的立体
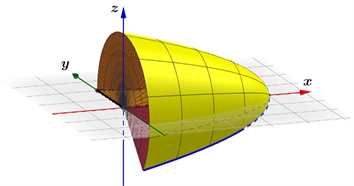
Figure 2. In Example 1, the process by which the enclosed plane region rotates about the x axis
图2. 实例1中所围平面区域绕x轴旋转的过程
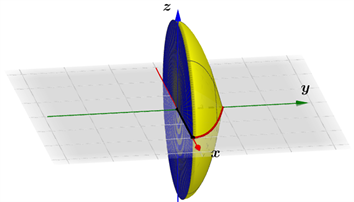
Figure 3. In Example 1, a solid formed by rotation of the enclosed plane region about the y axis
图3. 实例1中所围平面区域绕y轴旋转形成的立体
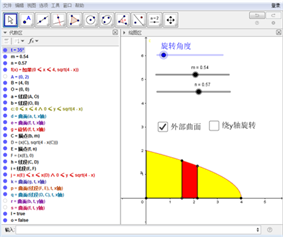
Figure 4. Algebra area and plot area of Example 1
图4. 实例1的代数区和绘图区
3. 基于“扣洞法”,利用GeoGebra动态演示旋转体的形成过程
3.1. 实例2的计算方法
实例2:由
和
所围成的图形绕y轴旋转,计算所得旋转体的体积。
按照文献 [2] 中的描述,按照如下公式计算体积
扣洞法:
(3)
3.2. 关于实例2的GeoGebra软件操作步骤
1) 分别打开绘图区、3D绘图区、代数区。
2) 在绘图区建立滑动条t,类型为角度,范围0度到360度。
3) 指令栏分别输入:
f(x) = 如果(2 ≤ x ≤ 6, −0.5(x − 4)2 + 2),g(x) = 如果(2 ≤ x ≤ 4, −0.5(x − 4)2 + 2),
h(x) = 如果(4 ≤ x ≤ 6, −0.5(x − 4)2 + 2)。
说明:建立曲线方程。
4) 指令栏分别输入:
A = (2, 0),B = (6, 0),C = (4, 2),D = (0, 2),O = (0, 0),
a = 线段(A, O),b = 线段(B, O),c = 线段(C, D),d = 线段(O, D),e = 线段(B, A),
i: 2 ≤ x ≤ 6 Ù 0 ≤ y ≤−0.5(x − 4)2 + 2。
在对象i的属性中将样式的线径调整为0,以便去掉不需要的线条。
说明:建立平面图形区域。
5) 指令栏分别输入:
j = 曲面(g, t, y轴),k = 曲面(h, t, y轴),l = 曲面(e, t, y轴),m = 曲面(c, t, y轴),n = 曲面(a, t, y轴)。
说明:平面图形区域绕y轴旋转。
6) 指令栏分别输入:
p = 曲面(ucos(t), sf(u), -usin(t), u, 2, 4, s, 0, 1),q = 曲面(ucos(t), sf(u), -usin(t), u, 4, 6, s, 0, 1)。
说明:加强显示效果。
7) 在绘图区建立“复选框”,在下拉列表中选取“曲面k”,标题改为“外部曲面”在绘图区建立“复选框”,在下拉列表中选取“曲面m”,标题改为“内部立体”。
3.3. 操作说明
通过滑动条t演示旋转体的生成过程,通过鼠标在3D绘图区拖动,可以从各个视角观察图形。通过复选框,可以观察外部旋转体和内部旋转体的结构。
图5——内部结构;图6——整体结构;图7——所围平面区域绕y轴旋转形成的立体;图8——所围平面区域绕y轴旋转的过程;图9——代数区和绘图区。
3.4. 旋转体的体积公式(3)的数学本质
通过动态演示,直观体会到公式(3)的两个定积分之差对应空间两部分旋转体的体积之差。
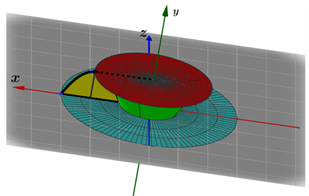
Figure 5. The internal structure of Formula (3)
图5. 公式(3)的内部结构
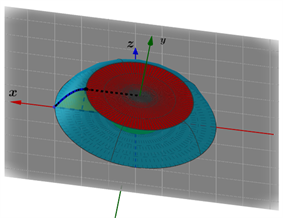
Figure 6. The overall structure of Formula (3)
图6. 公式(3)的整体结构
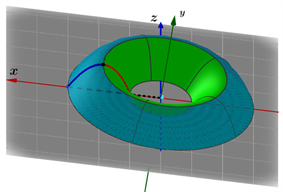
Figure 7. In Formula (3), a solid formed by rotation of the enclosed plane region about the y axis
图7. 公式(3)中所围平面区域绕y轴旋转形成的立体
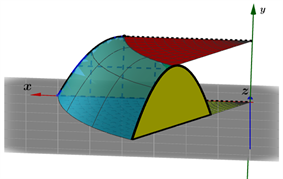
Figure 8. In Formula (3), the process by which the enclosed plane region rotates about the y axis
图8. 公式(3)中所围平面区域绕y轴旋转的过程
Figure 9. Algebraic area and plot area of Formula (3)
图9. 公式(3)的代数区和绘图区
4. 基于“套筒法”,利用GeoGebra动态演示旋转体的形成过程
按照文献 [2] 中288页的描述,按照如下公式计算体积
套筒法:
(4)
4.1. 关于实例2的GeoGebra软件操作步骤
1) 分别打开绘图区、3D绘图区、代数区。
2) 在绘图区建立滑动条t,类型为角度,范围0度到360度;滑动条m,n,类型为数值,范围0到1,增量为0.01。
3) 指令栏分别输入:
f(x) = 如果(2 ≤ x ≤ 6, −0.5(x − 4)2 + 2),A = (2, 0),B = (6, 0),a = 线段(A, B),b = 线段(A, B),
s: 2 ≤ x ≤ 6 Ù 0 ≤ y ≤ −0.5(x − 4)2 + 2。
在对象s的属性中将样式的线径调整为0,以便去掉不需要的线条。
说明:建立平面图形区域。
4) 指令栏分别输入:
c = 曲面(f, t, y轴),d = 曲面(a, t, y轴)。
说明:平面图形区域绕y轴旋转。
5) 指令栏分别输入:
C = 描点(a, m),D = 描点(b, n),E = (x(C), f(x(C))),F = (x(D), f(x(D))),e = 线段(C, E),g = 线段(D, F),h = 线段(C, D),i = 如果(x(C) ≤ x ≤ x(D), −0.5(x − 4)2 + 2), j:x(C) ≤ x ≤ x(D) Ù 0 ≤ y ≤ −0.5(x − 4)2 + 2。
将对象j的属性中将样式的线径调整为0,以便去掉不需要的线条。
说明:建立参数可调节的微元平面图形区域。
6) 指令栏分别输入:
k = 曲面(e, t, y轴),p = 曲面(g, t, y轴),q = 曲面(h, t, y轴),r = 曲面(i, t, y轴)。
说明:微元区域平面图形区域绕y轴旋转。
7) 指令栏分别输入:
v = 曲面(ucos(t), sf(u), -usin(t), u, 2, 6, s, 0, 1),w = 曲面(ucos(t), sf(u), -usin(t), u, x(C), x(D), s, 0, 1)。
说明:加强显示效果。
4.2. 操作说明
通过滑动条t演示旋转体的生成过程,通过鼠标在3D绘图区拖动,可以从各个视角观察图形。通过滑动条m、n演示微元的变化。可以在绘图区添加文本框来完善显示效果。
图10——微元图形区域绕y轴旋转形成的立体;图11——所围平面区域绕y轴旋转的过程;图12——代数区和绘图区。
4.3. 套筒法的微积分思想
通过动态演示体会“线动成面、面动成体”的微积分思想,认识公式(4)中的被积函数就是由一条线绕旋转轴旋转而得到的一圈曲面的面积。在积分变量的取值范围内,这圈曲面以旋转轴为中心内外连续变动就生成了旋转体,这些无限个面累加形成体积的过程就是积分。
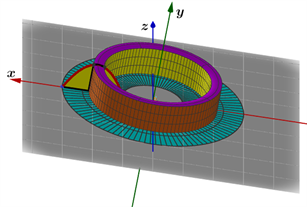
Figure 10. In Formula (4), the solid formed by rotation of the element graph region about the y axis
图10. 公式(4)中微元图形区域绕y轴旋转形成的立体
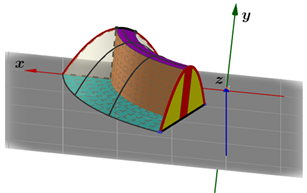
Figure 11. In Formula (4), the process by which the enclosed plane region rotates about the y axis
图11. 公式(4)中所围平面区域绕y轴旋转的过程
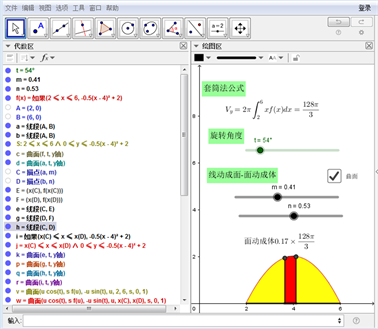
Figure 12. Algebraic area and plot area of Formula (4)
图12. 公式(4)的代数区和绘图区
5. 结束语
GeoGebra动态数学软件将代数窗口与图形绘制窗口完美结合,在高等数学课程的教学过程中表现卓越,大大提高了学生的学习兴趣与热情,丰富了课堂内容。利用GeoGebra数学软件进行辅助教学,将高等数学概念的形成过程进行思维可视化,使学生透过抽象的公式,看到它所代表的图形以及深刻的微积分思想,不但对数学表达式理解更透测,而且能够感受到数学语言的魅力。教师在高等数学课程的教学过程中利用GeoGebra软件设计教学方案,创建用作演示的交互式应用程序,将传统的教学观念与模式进行改革创新,进而提高课程的教学质量。
目前,GeoGebra 软件与高等数学课程的结合还处于起步阶段,在文献 [3] [4] [5] 中,关于GeoGebra在高等数学中的应用做了初步的探讨。GeoGebra与高等数学的深入融合还有很大的发展空间,将 GeoGebra软件融入高等数学课堂,优化课堂教学结构已成为必然趋势,这还需要进一步的探索和研究,且是任重道远的。