基于精确准直线阵探测器的康普顿背散射成像仿真

Compton Backscatter Imaging Simulation Based on Precise Collimated Linear Array Detector

摘要: 常规的康普顿背散射成像图像重建方法有精准对焦法和能谱解析法两种。传统精准对焦法需逐点扫描，扫描时间长并且射线利用率低下；能谱解析依赖高时间分辨率的探测器，获得的能谱数据有限，且重建算法的计算复杂度高，耗时较长。故本文在精准对焦方法的前提上提出基于线阵探测器的康普顿背散射成像系统，使线阵探测器只接收来自固定散射角度且具有固定能量的背散射光子，缩短了探测时长且提高了射线利用率。后续图像重建过程中考虑射线衰减，无需利用能谱数据仅利用线阵探测器收集到的背散射光子数信息即可完成衰减校正，得到待测物体内部各点电子密度进而获得重建图像。本文利用蒙特卡罗方法，建立仿真模型，完成康普顿背散射成像过程的仿真，经理论计算完成衰减校正，得到物体内各点电子密度以及重建后图像。

Abstract: Conventional Compton backscatter imaging image reconstruction methods include precise focusing and energy spectrum analysis. Accurate focusing requires point-by-point scanning, long scanning time and low ray utilization; energy spectrum analysis relies on high-time resolution detectors, which can obtain limited energy spectrum data, and the reconstruction algorithm has high computational complexity and time-consuming. Therefore, this paper proposes a Compton backscatter imaging system based on a linear array detector on the premise of a precise focusing method. A collimator is installed on each detection unit of the ray source and the linear array detector to determine the incident source and the linear array. After the spatial position of the detector, the linear array detector can only receive backscattered photons from a fixed scattering angle and with a fixed energy, and the object to be measured is divided into several unit blocks. Each unit block is scanned, and each time the linear array detector is scanned, the depth-photon number information of the corresponding unit block can be obtained to complete the backscattered photon positioning. In the subsequent image reconstruction process, the ray attenuation is considered, and the attenuation correction can be completed by using only the backscattered photon information collected by the linear array detector without using the energy spectrum data, and the electron density of each point inside the object to be measured is obtained to obtain the reconstructed image. This paper uses the Monte Carlo method to establish a simulation model to complete the simulation of the Compton backscatter imaging process. After theoretical calculation, the attenuation correction is completed, and the electron density of each point in the object and the reconstructed image are obtained.

1. 引言

透射式X射线成像技术作为目前较为成熟的无损检测手段，广泛应用于工业、医疗、安防等领域 [1]。但是其存在着些许问题，如根据有效原子序数信息很难准确地从不同种物质中识别出危险品 [2]，对空间几何结构复杂且不规则物体的检测也是难题，而康普顿背散射成像技术在处理这些问题时有很好的效果。其射线源与探测器位于待测物体同一侧，在待测物体的任意一侧即可测量物体不同空间位置的康普顿背散射光子数与散射光子能量，进而通过图像重建技术对散射光子信息加以利用，最终得到具有待测物体内部结构信息的康普顿背散射重建图像。适合对车辆、人员、大型货物等大物体进行隐蔽检测；且其对低原子序数物质十分敏感，对毒品、炸药等的检测十分合适 [3]。

康普顿背散射成像图像重建方法分为精准对焦法与能谱解析法，传统精准对焦方法对射线利用率低并且由于是逐点扫描使得扫描时间过长 [4]；而能谱解析方法比较依赖高时间分辨率的能谱探测器，且由于是探测背散射光子，故接收到的能谱数据范围有限，即便利用迭代法可以忽视能谱数据不足这一问题，但迭代法的耗时更长，并且计算过程比较繁琐 [5]。本课题提出的基于线性探测器的康普顿背散射成像系统，无需利用背散射能谱数据，因为线阵探测器与入射X射线间的角度固定后，再加上线阵探测器上每个探测单元前方的准直器，使得探测器只能接受到固定散射角度来的散射光子，而散射光子能量只由入射光子能量E₀和散射角度θ决定，目前散射角度θ和入射能量E₀都已确定，则探测器上接收到的光子能量就是固定的E₁。并且通过蒙特卡洛方法 [6] 进行计算能够得到线阵探测器中每个探测单元对应的物体内部中各深度散射点的散射光子数，后续经理论计算完成衰减校正得到各散射点的准确的电子密度，最终完成图像重建。

2. 康普顿散射

2.1. 康普顿散射原理

X射线通过实物物质发生散射时，散射光中除了有原波长λ₀的X射线外，还产生了波长λ大于λ₀的X射线，其波长的增量随散射角的不同而变化。这种现象称为康普顿散射，亦称康普顿效应。

康普顿散射过程发生在入射射线光子与靶物质原子核外电子之间，如图1所示。入射X射线光子与靶原子核外电子发生碰撞，碰撞后的光子并没有消失，而只是损失了自己的部分能量给电子。能量损失后的X光子改变运动方向后继续在物质中穿行，而获得能量后的电子则脱离原子核的约束成为反冲电子 [7]。

Figure 1. Compton scattering diagram

图1. 康普顿散射示意图

入射光子的能量E₀，康普顿散射光子的能量E₁以及散射角之间的关系，符合康普顿方程，可以根据能量守恒定律与动量守恒定律求得。通过推导计算能够得到波长改变量Δλ与散射光子能量E₁为：

$\Delta \lambda =\lambda -{\lambda }_0=\frac{c}{\nu }-\frac{c}{{\nu }_0}=\frac{h}{m_{0}c}\left(1-\cos \theta \right)$ (1)

其中h为普朗克常数；c为光速；m₀为静态电子质量；θ为康普顿散射的散射角。

$E_1=\frac{E_0}{1+\alpha \left(1-\cos \theta \right)}$ (2)

$\alpha =\frac{h\upsilon }{m_0{c}^2}=\frac{h}{m_{0}c}\times \frac{\upsilon }{c}=\frac{{\lambda }_e}{\lambda }$

其中E₀为入射光子能量；λ_e为电子的康普顿散射波长；λ为入射光子的波长，康普顿散射只有在入射光子的波长与电子的康普顿波长相比拟时，散射才显著，所以α的值可判别康普顿散射是否显著。由上式可以看出散射光子能量E₁只与入射光子能量E₀和散射角θ有关。

2.2. 康普顿微分散射截面

康普顿微分散射截面的意义是一个能量为 $h\upsilon$ 的入射光子与原子中的一个核外电子作用后被散射到θ方向单位立体角里的概率 [8] (记作 $\frac{\text{d}\sigma \left(E_0,\theta \right)}{\text{d}\Omega }$，单位：cm²/单位立体角)，为：

$\begin{array}{l}\frac{\text{d}\sigma \left(E_0,\theta \right)}{\text{d}\Omega }=\frac{r_e^2}{2}\left(\frac{E_0}{E_1}+\frac{E_1}{E_0}-{\sin }^2\theta \right){\left(\frac{E_1}{E_0}\right)}^2\\ =\frac{r_e^2}{2}\left[{\cos }^2\theta +\alpha \left(1-\cos \theta \right)+\frac{1}{1+\alpha \left(1-\cos \theta \right)}\right]{\left[\frac{1}{1+\alpha \left(1-\cos \theta \right)}\right]}^2\\ =r_e^2{\left[\frac{1}{1+\alpha \left(1-\cos \theta \right)}\right]}^2\left[\frac{1+{\cos }^2\theta }{2}\right]\left[1+\frac{{\alpha }^2{\left(1-\cos \theta \right)}^2}{\left(1+{\cos }^2\theta \right)\left[1+\alpha \left(1-\cos \theta \right)\right]}\right]\end{array}$ (3)

其中r_e为经典电子半径， $r_e=e/m_0{c}^2=2.8\times {10}^{-13}\text{cm}$ ；E₁为散射角度为θ时的散射光子能量；E₀为入射光子能量。由上述公式可看出，康普顿微分散射截面只与入射光子能量E₀和散射角θ有关，当入射光子能量一定时，微分散射截面只与散射角有关 [9]。不同能量下的微分散射截面与散射角度的关系如图2所示，由图可见，随着入射光子能量的降低，微分散射截面逐渐增加，背散射概率增大。

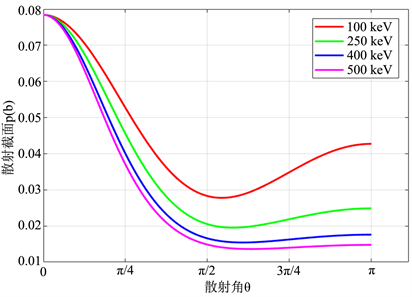
Figure 2. The relationship of differential scattering cross section with incident photon energy and scattering angle

图2. 微分散射截面与入射光子能量及散射角度的关系图

2.3. 射线衰减校正

射线穿过物质时，主要发生光电效应、康普顿效应和电子对效应 [10]，这几种效应都会使入射线的方向改变、射线强度发生衰减，物质衰减系数如下式所示：

$\mu ={\mu }_{光电效应}+{\mu }_{康普顿效应}+{\mu }_{电子对效应}$ (4)

而在入射线能量介于0.3 MeV~2 MeV时康普顿效应 [11] 占据主要地位，其余两种效应可忽略。

而 [12]

${\mu }_{康普顿效应}=\sigma \left(E\right)\cdot \frac{N_A\cdot \rho }{A}$ (5)

$\sigma \left(E\right)$ 为单个原子的康普顿散射截面，有 [13]：

$\sigma \left(E\right)=Z\cdot {\sigma }_c\left(E\right)$ (6)

${\sigma }_c\left(E\right)$ 为单个电子的康普顿散射截面，是单个电子的康普顿微分散射截面对整个立体角的积分：

${\sigma }_c=2\pi r_e^2\left\{\frac{1+\alpha }{{\alpha }^2}\left[\frac{2\left(1+\alpha \right)}{1+2\alpha }-\frac{\ln \left(1+2\alpha \right)}{\alpha }\right]+\frac{\ln \left(1+2\alpha \right)}{2\alpha }-\frac{1+3\alpha }{{\left(1+2\alpha \right)}^2}\right\}$ (7)

$\alpha =\frac{E}{\text{2}\pi m_0{c}^2}$

则上式可化成 [14]

${\mu }_{康普顿效应}={\sigma }_c\left(E\right)\cdot \frac{N_A\cdot \rho }{A}\cdot Z$ (8)

而

${\rho }_e=\rho \cdot N_A\cdot \frac{Z}{A}$ (9)

最终可得：

${\mu }_{康普顿效应}={\sigma }_c\left(E\right)\cdot {\rho }_e$ (10)

散射光子数公式如下所示：

$n=n_0\times \frac{\text{d}\sigma }{\text{d}\Omega }\left(E_0,\theta \right)\times \text{d}V\times \text{d}\Omega \times {\rho }_e\times f_i\left(E_0\right)\times f_s\left(E_1\right)\times k$ (11)

$\begin{array}{l}{f}_i\left(E_0\right)={\text{e}}^{-{\displaystyle {\int }_a^r\mu \left(l\right)\text{d}l}}\\ f_s\left(E_1\right)={\text{e}}^{-{\displaystyle {\int }_r^b\mu \left(l\right)\text{d}l}}\end{array}$

n为接收到的背散射光子数；n₀为入射光子数； $\frac{\text{d}\sigma }{\text{d}\Omega }\left(E_0,\theta \right)$ 为康普顿微分散射截面； $\text{d}V=\text{d}S\ast \text{d}z$ 代表着单次测量的有效体积，dS为射线束的横截面积，dz是入射线方向上的一个线元；dΩ是探测器对散射点所张的立体角； $f_i\left(E_0\right)$ 代表入射线到达散射点前的入射衰减、 $f_s\left(E_1\right)$ 代表散射点到达探测器前的出射衰减，其中 $\mu \left(l\right)$ 为线性衰减系数值；k为探测器的探测效率。

本文进行理论推导时，认为探测器收集到的光子是对应深度的散射点发生散射得到的固定散射角度的散射光子，在实际情况中由于探测器尺寸的限制，导致每个探测单元接收到的是多个散射点散射的固定散射角的散射光子的集合。引入平均的思想对该问题加以讨论，能够得出：探测单元的尺寸决定了对物体深度信息获取的精度。

已知线性衰减系数表达式后，将表达式代入入射线和散射线的衰减公式中，最终能够得到该点的电子密度，完成对衰减的校正，实现图像重建，如下式所示：

$n=n_0\cdot k\cdot \frac{\text{d}\sigma }{\text{d}\Omega }\left(E_0,\theta \right)\cdot \text{d}S\cdot \text{d}z\cdot \text{d}\Omega \cdot {\rho }_e\cdot \exp \left(-{\displaystyle {\int }_A^X{\rho }_e\cdot {\sigma }_c\left(E_0\right)\text{d}l}\right)\cdot \exp \left(-{\displaystyle {\int }_X^C{\rho }_e\cdot {\sigma }_c\left(E_{\text{1}}\right)\text{d}l}\right)$ (12)

${\rho }_e\cdot \exp \left(-{\displaystyle {\int }_A^X{\rho }_e\cdot {\sigma }_c\left(E_0\right)\text{d}l}\right)\cdot \exp \left(-{\displaystyle {\int }_X^C{\rho }_e\cdot {\sigma }_c\left(E_{\text{1}}\right)\text{d}l}\right)=\frac{n}{n_0\cdot k\cdot \frac{\text{d}\sigma }{\text{d}\Omega }\left(E_0,\theta \right)\cdot \text{d}S\cdot \text{d}z\cdot \text{d}\Omega }$ (13)

根据上式可以看出，电子密度ρ_e待求，而其他不含ρ_e的项都为常数，对于入射线衰减和散射线衰减的表达式可以做以下讨论。

dl为入射线方向上的一个线元，将衰减系数的表达式中的积分变成求和后，dl不再是趋于无限小，而是一个可根据探测单元尺寸求出的定值Δl，这样就把求解每个散射点的电子密度变成求解每个散射单元的平均电子密度的问题了。

$\begin{array}{l}{\displaystyle {\int }_A^X{\rho }_e\cdot {\sigma }_c\left(E_0\right)\text{d}l}\approx {\sigma }_c\left(E_0\right)\cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\rho }_{ei}}\\ {\displaystyle {\int }_X^C{\rho }_e\cdot {\sigma }_c\left(E_1\right)\text{d}l}\approx {\sigma }_c\left(E_1\right)\cdot {\displaystyle \underset{i=1}{\overset{m}{\sum }}{\rho }_{ei}}\end{array}$ (14)

${\rho }_e\cdot \exp \left(-{\sigma }_c\left(E_0\right)\cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\rho }_{ei}}\right)\cdot \exp \left(-{\sigma }_c\left(E_1\right)\cdot {\displaystyle \underset{j=\text{0}}{\overset{m}{\sum }}{\rho }_{ej}}\right)=\frac{n}{n_0\cdot k\cdot \frac{\text{d}\sigma }{\text{d}\Omega }\left(E_0,\theta \right)\cdot \text{d}S\cdot \text{d}z\cdot \text{d}\Omega }$ (15)

$\begin{array}{l}{\rho }_e\cdot \exp \left(-{\sigma }_c\left(E_0\right)\cdot {\displaystyle \underset{i=1}{\overset{n\text{-1}}{\sum }}{\rho }_{ei}}-{\sigma }_c\left(E_0\right)\cdot {\rho }_e\right)\cdot \exp \left(-{\sigma }_c\left(E_1\right)\cdot {\rho }_e-{\sigma }_c\left(E_1\right)\cdot {\displaystyle \underset{j=1}{\overset{m}{\sum }}{\rho }_{ej}}\right)\\ =\frac{n}{n_0\cdot k\cdot \frac{\text{d}\sigma }{\text{d}\Omega }\left(E_0,\theta \right)\cdot \text{d}S\cdot \text{d}z\cdot \text{d}\Omega }\end{array}$ (16)

$\begin{array}{l}{\rho }_e\cdot \exp \left\{-\left[{\sigma }_c\left(E_0\right)+{\sigma }_c\left(E_1\right)\right]\cdot {\rho }_e\right\}\cdot \exp \left\{-\left[{\sigma }_c\left(E_0\right)\cdot {\displaystyle \underset{i=1}{\overset{n\text{-1}}{\sum }}{\rho }_{ei}}+{\sigma }_c\left(E_1\right)\cdot {\displaystyle \underset{j=1}{\overset{m}{\sum }}{\rho }_{ej}}\right]\right\}\\ =\frac{n}{n_0\cdot k\cdot \frac{\text{d}\sigma }{\text{d}\Omega }\left(E_0,\theta \right)\cdot \text{d}S\cdot \text{d}z\cdot \text{d}\Omega }\end{array}$ (17)

具体实现办法，将样品在xoy面分解成如p * q个待测物体单元，首先从最上方的一行从左往右的利用线阵探测器(假设有n个探测单元)进行散射光子的获取，因为最上一行不用担心散射线的衰减，因为发生散射后直接出射出物体了，不会进入其他单元中，因此最上一行中的散射衰减系数 = 1，此时对于入射线的衰减系数来说， $n=1,2,3,\cdots$，散射深度nΔl，从n = 1开始计算，利用n = 1时求得的电子密度求n = 2的电子密度，最终求得n个点的电子密度，完成该待测物体单元上各个深度对应的散射单元的电子密度的计算。我们可以通过式(16)公式计算出最上面一层的电子密度。

式(15)右侧为定值，左侧含E₀的是入射衰减，入射衰减的距离为nΔl；含E₁的是散射衰减，在计算第一层时为1。m为散射线穿过的上层散射单元的数量

紧接着是第二层，在第二层发生的若干散射单元发出的散射线，由于本课题带有准直器的线阵探测器，待测样品间的夹角是固定的，所以很容易就能够知道散射线穿过第一层的哪些散射单元，而这些散射单元的电子密度我们在求第一层时已经得到了，所以将已知的数据代入到式(17)中，可得到第二层中各散射单元的平均电子密度了。经过多次计算，最终得到p * q * n的三维空间电子密度图，之后对p * q * n的电子密度数据进行处理，完成电子密度–灰度的转换，最终输出一幅二维的代表着电子密度投影的灰度图像，完成图像重建。

3. 康普顿背散射成像模型

X射线源发射X射线至待测物体，根据待测物体的xyz空间中的坐标范围可构建一个宽高长为x₁, y₁, z₁的长方体，示意图如图3所示，将长方体在xoy面分解成m × n个 $\frac{x_1}{m}\times \frac{y_1}{n}\times z_1$ 的单元块，对每个单元块进行一次扫描(确定射线源和探测器与长方体的空间夹角不变，整体在xoy面平移)，总计m × n次扫描，即可完成对待测物体的深度–背散射光子数信息的获取。

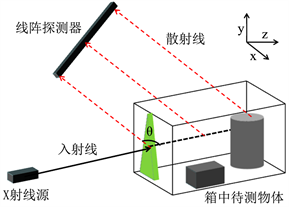
Figure 3. Schematic diagram of Compton backscatter imaging system

图3. 康普顿背散射成像系统示意图

4. 蒙特卡罗模拟计算

4.1. 基于Geant4的蒙特卡洛模拟

Geant4 (Geometry And Tracking)是由欧洲核子中心(CERN)开发的一套C++开源工具包，其用途是模拟粒子在物质中的物理过程。Geant4由于C++强大的语言能力，因而能够灵活地处理规模更加庞大、结构更加复杂的物理环境。Geant4几乎可以模拟所有物理过程，包括电磁相互作用、中子散射、光学过程等。除了在高能物理方面的应用，Geant4还被广泛应用于核物理、空间和天体物理、医用物理、辐射防护和探测等。

4.2. 在Geant4中的仿真模型的建立

选定用能量为300 keV的X射线束作为光源，位置(0, 0, 0)；待测物体前端距离光源2 cm，待测物体为一个长宽高为5 cm的碳块和长宽高为3 cm的铁块(两个物体中心点在一条直线上)；线阵探测器起点位于(0, 4.5, −2.5),空间向量为(0, 1, 1)，其上具有20个探测单元，每一个探测单元都设置一个准直器，仿真模型如图4所示。为验证仿真结果的准确性，本文对仿真模型进行一定修改，利用具备能谱分辨能力的单元探测器替代探测单元及对应的准直器，应用修改后的仿真模型进行验证实验，将本文仿真实验结果与验证实验结果进行对比分析。

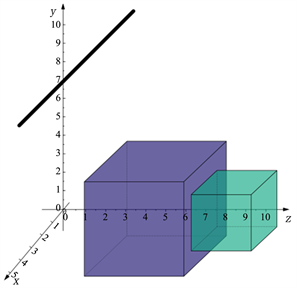(a) 实验物理模型 (b) Geant4中仿真模型

Figure 4. Simulation model diagram

图4. 仿真模型图

4.3. 仿真结果与分析

将三维待测物体在xoy面分为20 * 20个单元块，每个单元块的深度为8 cm，对每个单元块进行一次仿真模拟，最终得到400个深度–光子数曲线，利用上述衰减校正模型进行计算，得到400个深度–电子密度曲线，进行电子密度–灰度的转换，进而完成图像重建，得到康普顿背散射灰度图像。400次背散射模拟中按射线与不同种类物质作用可大致分为三类，分别为射线经过前端碳块再经过后端铁块、射线经过前端碳块并经过铁块边界以及射线只经过碳块。为此本文只列出符合这三类条件的三次背散射模拟过程得到的深度–光子数曲线，如图5所示，以及验证实验得到的深度–光子数曲线，如图6所示。本文所选取的三个单元块中心在xoy面上的坐标为(0.125, 0.125)、(1.375, 0.125)、(1.875, 0.125)，并以中心坐标作为每个单元块的代号。

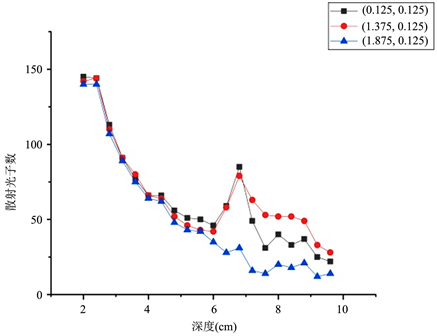
Figure 5. Depth-scattering photon numbers

图5. 深度–散射光子数

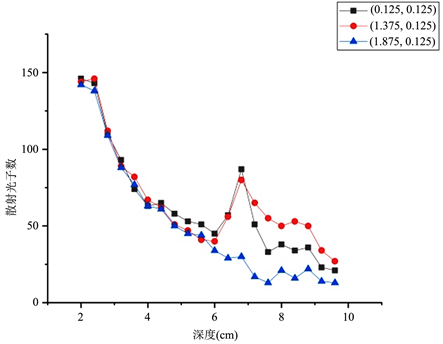
Figure 6. Depth-scattering photon numbers of confirmatory experiment

图6. 验证实验的深度–散射光子数曲线

验证实验首先基于能谱探测单元获取了每个单元块的不同深度的能谱信息，在能谱已知的情况下获取能谱中固定散射能量(本文中为150 keV)的散射光子数，进而将各个深度的符合300 keV能量条件的散射光子数绘制成深度–散射光子数曲线。为节省篇幅，本文只列出(0.125, 0.125)、(1.375, 0.125)、(1.875, 0.125)这三个具有不同特征的单元块中三个深度(4 cm、6 cm、8 cm)条件下的能谱图，如图7~9所示，其中每幅图的横轴代表散射光子的能量，单位为keV；纵轴代表散射光子数量。

Figure 7. Energy spectrum at different depths of (0.125, 0.125) unit block

图7. (0.125, 0.125)单元块不同深度能谱图

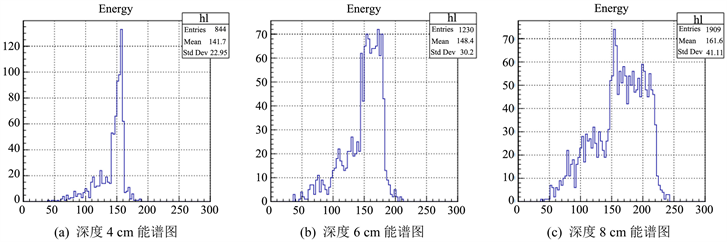
Figure 8. Energy spectrum at different depths of (1.375, 0.125) unit block

图8. (1.375, 0.125)单元块不同深度能谱图

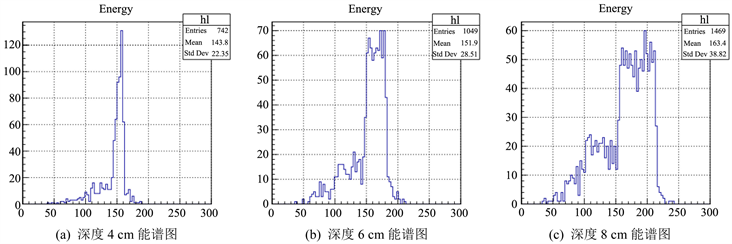
Figure 9. Energy spectrum at different depths of (1.875, 0.125) unit block

图9. (1.875, 0.125)单元块不同深度能谱图

通过对比分析，图5与图6可看出两幅图中对应单元曲线并无太大差异，与本实验的仿真结果相符。

利用上文2.3小节中电子密度计算公式计算出忽略衰减的电子密度与衰减校正后的电子密度，并将计算结果绘制成衰减未校正和校正后的电子密度曲线，如图10、图11所示。将每一单元块对应深度的衰减未校正和校正后的电子密度计算出来，取其投影值，能够获得未衰减校正的背散射图像与衰减校正后的背散射图像，如图12、图13所示。

Figure 10. Depth-uncorrected electron density

图10. 深度–未校正电子密度

Figure 11. Depth-corrected electron density

图11. 深度–校正后电子密度

Figure 12. Image without attenuation correction

图12. 未衰减校正图像

Figure 13. Image after attenuation correction

图13. 衰减校正后图像

由于图12在人眼看来一片漆黑，无法获取有效信息，但需对图12与图13进行比较，故将未衰减校正图像与衰减校正后图像进行归一化，即灰度拉伸，如图14、图15所示.同时引入虚拟原图对归一化后的两幅图像进行客观图像质量评价，虚拟原图即理想情况下的图像，由真实的碳和铁电子密度的投影得到，如图16所示。图像质量评价结果如表1所示。

Figure 14. Image without attenuation correction after stretching

图14. 拉伸未衰减校正图像

Figure 15. Attenuation correction image after stretching

图15. 拉伸衰减校正后图像

Table 1. Image quality evaluation results

表1. 图像质量评价结果

Figure 16. Virtual original

图16. 虚拟原图

图像质量评价如表1所示，图像的信息熵表示图像中灰度分布的聚集特征所包含的信息量，由于本文选择的待测物体属于规则图像，故信息量较小，但图15的信息熵较图14提升18.8%左右，这说明对衰减进行校正能够有效地提升灰度图像包含的信息量。

灰度方差反映了图像的对比度和清晰度，方差越大则对比度越高，清晰度越高。衰减校正后图像的灰度方差要比未进行衰减校正图像高出一个量级还要多，而通过人眼观察也能看出图15的对比度与清晰度要远高于图14。

而图像的峰值信噪比是通过计算待评的图像与参考的图像之间像素灰度的比值以及误差的变化大小来进行全局评价，其值越大，表明待评图像与参考图像之间的失真越小，待评图像质量越好。由评价结果可以看出，图15的峰值信噪比的值要较图14提升了85.8%，这说明图15的失真程度要低于图14，更接近于虚拟原图。

5. 结论

本文基于线阵探测器进行了康普顿背散射成像仿真，利用Geant4程序模拟背散射过程，确定线阵探测器与源及待测物体的空间位置，线阵探测器接收固定能量的背散射光子，后续图像重建中对物质衰减作用进行校正，区别于以往的能谱解析重建与精准对焦重建方法，本文提出的方法无需利用背散射能谱数据，仅靠背散射光子数即可完成衰减校正，并且每次扫描能够获得一个物体单元块的深度–光子数信息，大大提升了重建效率。对衰减校正图像与未经衰减校正图像进行图像质量评价，从评价结果可看出衰减校正图像远优于未校正图像。故本文所提出的理论与方法为接下来的康普顿背散射相关工作提供了一定参考依据。

NOTES

^*通讯作者。