基于相对利润最大化的混合寡头博弈的复杂动态性

Complex Dynamics in a Mixed Duopoly Game Based on Relative Profit Maximization

摘要: 本文研究价格–产量混合寡头博弈模型的复杂动力学行为。基于相对利润最大化和有限理性预期原则，在成本函数为线性的情况下，构建相应的离散动态系统。在理论上，给出了纳什均衡点局部稳定性满足的条件。在数值实验方面，利用分岔图描绘了两种情况下产品差异性、调整速度等参数对纳什均衡点稳定性的影响。

Abstract: In this paper, the complex dynamic behavior of a mixed duopoly game model is studied. Based on the principle of relative profit maximization and bounded rational expectation, in the case that the cost function is linear, the corresponding discrete dynamic system is constructed. In theory, the conditions for local stability are given. In terms of numerical experiments, bifurcation diagrams are used to depict the effects of product differences, adjustment speed and other parameters on the stability of Nash equilibrium in two cases.

1. 引言

寡头市场指的是一个市场同时存在数量有限的企业，不同市场主体在同一市场进行不完全竞争。在市场经济中，产品价格在消费者选择过程中占据较大权重，故价格竞争规律对于企业市场分析至关重要，同时产品数量也深刻影响着市场规律，也是市场价格竞争中的一个重要考量指标，所以对于产品价格与产品数量间寡头博弈规律的研究也就尤为重要。

近年来，国内外许多文献对于寡头博弈做了大量分析。Ma [1] 等人引入连续的时滞Bertrand双寡头模型，并研究具有时滞影响的复杂动态模型。Wang [2] 等利用技术创新研究了Bertrand双寡头博弈的复杂动力学问题。Zha [3] 等人研究了具有溢出效应的Bertrand双寡头博弈的纳什均衡稳定性。在 [4] 中，作者调查了供应链闭环Bertrand博弈的动态特性。文献 [5] 分析了具有等弹性需求的Cournot竞争中的战略授权模型。Elabasy等人 [6] 分析了具有线性需求函数和抛物线总成本函数的异质博弈。文献 [7] 中考虑了一种混合型Cournot-Bertrand双寡头博弈，在这种混合类型中不同的期望研究了线性需求和固定边际成本的博弈问题。Chen等人 [8] 引入具有线性需求的Bertrand三元博弈模拟了中国电信市场的竞争。文献 [9] 研究了一类具有时滞的线性连续Bertrand双寡头博弈模型。文献 [10] 研究动态Cournot的两种不同时滞结构，在参考文献中考虑了两个异质玩家的非线性博弈问题。假设在双寡头市场中玩家是异质的，文献 [11] 考虑不同的时间延迟结构下的非线性博弈模型。文献 [12] 也对非线性寡头垄断进行了研究。Torcicollo [13] 引入了非线性连续双寡头模型的自扩散和交叉扩散作用。文献 [14] 分析了一类描述具有边际成本的时间演化的非线性Stackelberg系统，研究了Nash均衡点的稳定性情况。Xin等人 [15] 针对两个产品尚处于初级阶段的寡头垄断企业提出非线性离散博弈模型。文献 [16] 也对Bertrand对策的非线性动力学进行了研究，在假设两家公司市场信息有限的条件下，研究了Cournot-Bertrand双寡头博弈。

上述文献都假设参加竞争的两家企业皆采取相同的竞争策略，如产量竞争和价格竞争。然而，一家企业采取价格策略而另一家企业采取产量策略的混合竞争广泛存在于实际产业中，它是完全产量竞争和价格竞争的一种中间结构。理论研究和经验观察表明，混合竞争策略对于市场均衡具有显著影响。Naimzada和Tramontana [17] 首次提出了线性成本下混合寡头博弈模型，并使用适应性调整机制研究均衡点的稳定性。

受文献 [17] 启发，本文研究混合寡头博弈模型的复杂动力学行为。与 [17] 不同，我们的模型基于相对利润最大化和有限理性预期原则，而 [17] 采用的是利润最大化以及适应性调整原则。在线性成本函数下，我们构建相应的离散动态系统，并研究纳什均衡点的稳定性，为企业动态市场竞争中的竞争策略提供理论支撑。

本文余下内容的安排如下：第2节给出模型的基本结构；第3节研究线性成本条件下系统均衡点的动态性质，并做数值分析；第4节是对全文的总结。

2. 混合寡头博弈模型

我们考虑一个需求函数为逆的差异化产品市场。这里假设市场宣传差异化产品给予消费者一定的优惠，其主要利益利用差异化产品。第一家公司以价格p₁生产数量q₁，而第二家公司以价格p₂生产数量q₂。在这里，竞争概况是 $p=\left(p_1,p_2\right)$，其中每个公司都希望根据利润最大化如下：

$\underset{p_i}{\text{Max}}{\pi }_i\left(p_i,p_{-i}\right)=q_i{p}_i-C_i\left(q_i\right)$ (1)

其中 $p_{-i}$ 指与企业i不同的另一家企业的价格， $C_i\left(q_i\right)$ 为成本函数。利用Singh和Vives介绍的消费者偏好，给出以下效用函数：

$U\left(q_1,q_2\right)=a\left(q_1+q_2\right)-\frac{1}{2}\left(q_1^2+q_2^2+2b{q}_1{q}_2\right);q_1,q_2>0$ (2)

简单的计算表明这个函数是严格凹的。使用限制条件 ${\displaystyle \underset{i=1}{\overset{2}{\sum }}{p}_i}{q}_i=1$ 和 $p_i=\frac{\partial U}{\partial q_i},i=1,2$，得到了价格函数如下：

$\{\begin{array}{l}{p}_1=a-q_1-b{q}_2\\ p_2=a-q_2-b{q}_1\end{array}$ (3)

参数a是一个正常数，其中两个公司的总产量都依赖于它且 $q_1+q_2=\frac{2a}{1+b}$，其中参数b衡量水平分化程度。如果b = 0，则市场由两个垄断企业控制；当b接近1时，两个公司的差异性变小；假设此参数为负值，意味着企业之间的互补性。

将p₁，q₂表示为q₁，p₂的函数，以下研究关于q₁，p₂的竞争模型：

$\{\begin{array}{l}{p}_1=a\left(1-b\right)-\left(1-b^2\right)q_1+b{p}_2\\ q_2=a-p_2-b{q}_1\end{array}$ (4)

3. 线性成本下的复杂动态性分析

在这项工作的博弈中，我们考虑一个线性成本函数：

$C_i\left(q_i\right)=c_i{q}_i,i=1,2$ (5)

则净利润表示如下：

$\begin{array}{l}{\pi }_1\left(q_1,p_2\right)=p_1{q}_1-C_1=\left[a\left(1-b\right)-\left(1-b^2\right)q_1+b{p}_2\right]q_1-c_1{q}_1\\ {\pi }_2\left(q_1,p_2\right)=p_2{q}_2-C_2=p_2\left(a-p_2-b{q}_1\right)-c_2\left(a-p_2-b{q}_1\right)\end{array}$ (6)

使每个公司的相对利润最大化以获得最佳产量需要，以下给出相对利润表达式：

$\begin{array}{l}{\prod }_1\left(q_1,p_2\right)={\pi }_1\left(q_1,p_2\right)-{\pi }_2\left(q_1,p_2\right)\\ {\prod }_2\left(q_1,p_2\right)={\pi }_2\left(q_1,p_2\right)-{\pi }_1\left(q_1,p_2\right)\end{array}$ (7)

将(6)式代入得到：

$\begin{array}{l}{\prod }_1\left(q_1,p_2\right)=G_1{q}_1-H_1{p}_2+E_1{q}_1^2+p_2^2+F_1{q}_1{p}_2\\ {\prod }_2\left(q_1,p_2\right)=-G_1{q}_1+H_1{p}_2-E_1{q}_1^2-p_2^2-F_1{q}_1{p}_2\end{array}$ (8)

其中 $E_1=b^2-1$， $F_1=2b$， $G_1=a\left(1-b\right)-\left(c_1+b{c}_2\right)$， $H_1=a+c_2$。

根据相对利润最大化的条件的 $\frac{\partial {\prod }_1}{\partial q_1}=0,\frac{\partial {\prod }_2}{\partial p_2}=0$，将(8)代入得到：

$\begin{array}{l}\frac{\partial {\prod }_1}{\partial q_1}=G_1+2E_1{q}_1+F_1{p}_2=0\\ \frac{\partial {\prod }_2}{\partial p_2}=-F_1{q}_1-2p_2+H_1=0\end{array}$ (9)

为了构建和研究这一博弈的动态特征，我们假设两个公司的行为都是理性的。理性行为意味着企业采用短视的调整机制，应用此机制需要公司只知道他们的相对利润是增加还是减少的信息。利用这个机制我们构建一个动态系统来描述这一博弈过程，如下所示：

$\begin{array}{l}{q}_1\left(t+1\right)=q_1\left(t\right)+k_1{q}_1\frac{\partial {\prod }_1}{\partial q_1}\\ p_2\left(t+1\right)=p_2\left(t\right)+k_2{p}_2\frac{\partial {\prod }_2}{\partial p_2}\end{array}$ (10)

式中，k₁，k₂为调整速度参数。

现对每个时间步长t施加稳态条件 $q_1\left(t+1\right)=q_1\left(t\right)$ 和 $p_2\left(t+1\right)=p_2\left(t\right)$，很容易得出上面的系统(10)具有唯一平衡点为 $e=\left(q_1^{\ast },p_2^{\ast }\right)$，其中，

$\begin{array}{l}{q}_1^{\ast }=\frac{a-c_1}{\text{2}}\\ p_2^{\ast }=\frac{\left(a+c_2\right)-b\left(a-c_1\right)}{\text{2}}\end{array}$ (11)

这个平衡点取决于参数a，b，c₁，c₂，实际上，其他参数k₁，k₂也影响了它的稳定性。

以下通过证明如下命题，确定该模型下平衡点的稳定性区域。

命题3.1：平衡点e是局部稳定的，如果

$0<\left(A_1{B}_1+{\mu }_1\right)k_1{k}_2<A_1{k}_1+B_1{k}_2<\frac{1}{2}\left(A_1{B}_1+{\mu }_1\right)k_1{k}_2+2$ (12)

其中 $A_1=-4E_1{q}_1^{\ast }-F_1{p}_2^{\ast }-G_1$， $B_1=F_1{q}_1^{\ast }+4p_2^{\ast }-H_1$， ${\mu }_1=F_1{}^2{q}_1^{\ast }{p}_2^{\ast }$。

证明：为了研究平衡点的稳定性，我们引用著名的稳定性条件，它建立在雅可比矩阵J的迹(T)及行列式(D)的基础上，对于一个二维的离散系统有如下线性方程组：

$\{\begin{array}{l}1-T+D>0\\ 1+T+D>0\\ 1-D>0\end{array}$ (13)

系统(10)在平衡点处的雅可比矩阵为：

$J=\left[\begin{array}{cc}1+\left(4E_1{q}_1^{\ast }+F_1{p}_2^{\ast }+G_1\right)k_1& F_1{q}_1^{\ast }{k}_1\\ -F_1{p}_2^{\ast }{k}_2& 1+\left(-F_1{q}_1^{\ast }-4p_2^{\ast }+H_1\right)k_2\end{array}\right]$ (14)

该矩阵的迹和行列式可变为

$\begin{array}{l}T=2-A_1{k}_1-B_1{k}_2\\ D=\left(1-A_1{k}_1\right)\left(1-B_1{k}_2\right)+{\mu }_1{k}_1{k}_2\end{array}$ (15)

因此上述稳定性条件可转化为

$\begin{array}{l}1-T+D>0\to \left(A_1{B}_1+{\mu }_1\right)k_1{k}_2>0\\ 1+T+D>0\to \left(A_1{B}_1+{\mu }_1\right)k_1{k}_2-2A_1{k}_1-2B_1{k}_2+4>0\\ 1-D>0\to A_1{k}_1+B_1{k}_2-\left(A_1{B}_1+{\mu }_1\right)k_1{k}_2>0\end{array}$ (16)

如果这三个条件没有同时满足，平衡点就会变得不稳定。因此，一旦违反了这些条件中的任一项，平衡点都会由于倍化分叉或Neimark-Sacker分叉而丧失其稳定性。经由简单的整理计算可以得到这些条件可转化为：

$0<\left(A_1{B}_1+{\mu }_1\right)k_1{k}_2<A_1{k}_1+B_1{k}_2<\frac{1}{2}\left(A_1{B}_1+{\mu }_1\right)k_1{k}_2+2$ (17)

综上，命题得证。

如前所述，(17)中的三个条件定义了调整速度k₁，k₂平面内的一个区域，其形状如图1所示的红色区域。第二个不等式是一个双曲线，若违反此条件，则出现倍周期分岔，平衡点将失去稳定性。直接关于平衡点稳定性的信息可以从图1中获得。很明显，红色区域平面保证了平衡点的局部稳定性。此外，这一稳定区域也受参数a和b的影响，当a接近10，且b接近1.2时，红色区域逐渐缩小。另一方面，当参数k₁，k₂从这个红色区域中取值时，平衡该点会因倍周期分岔而失去稳定性。以下我们考虑不同参数的取值对于平衡点行为的影响。

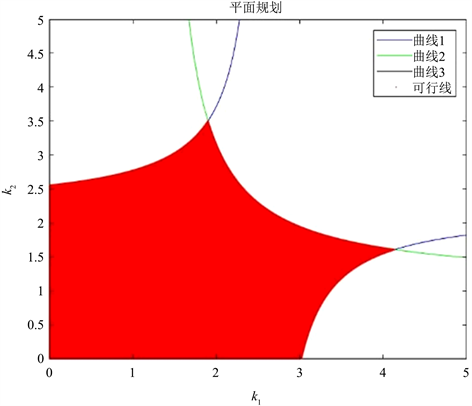
Figure 1. Stable region of equilibrium (parameter value a = 0.8, b = 0.2, c₁ = 0.11, c₂ = 0.12)

图1. 平衡点稳定区域(参数值a = 0.8, b = 0.2, c₁ = 0.11, c₂ = 0.12)

通过固定参数b = 1，c₁ = 2，c₂ = 2，k₁ = 0.1，k₂ = 0.1，得到q₁，p₂关于参数a的分歧图如图2所示，表明了倍周期分岔的出现导致系统平衡点的不稳定性。当 $a\in \left(0,10\right)$ 时，平衡点大致处于稳定状态，随着参数值的增加，出现倍周期分岔，最终导致混沌构建。

通过固定参数a = 10，c₁ = 2，c₂ = 2，k₁ = 0.1，k₂ = 0.1，得到q₁，p₂关于参数b的分歧图如图3所示。当 $b\in \left(0,1\right)$ 时，平衡点大致处于稳定状态，当b > 1时，平衡点逐渐失去稳定性，进入混沌区域。

Figure 2. Image of q₁, p₂ on varying the parameter a

图2. q₁，p₂随参数a变化图像

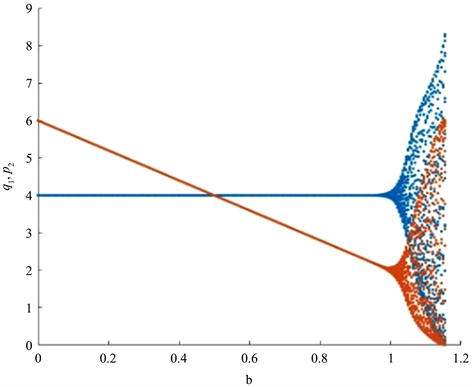
Figure 3. Image of q₁, p₂ on varying the parameter b

图3. q₁，p₂随参数b变化图像

通过固定参数a = 10，b = 1，c₂ = 2，k₁ = 0.1，k₂ = 0.1，得到q₁关于参数c₁的分歧图如图4所示，当c₁取接近0的参数值时，进入系统的混沌区域，而增加参数至c₁ > 3时，系统行为逐渐由复杂变为稳定。

通过固定参数a = 10，b = 1，c₁ = 2，k₁ = 0.1，k₂ = 0.1，得到p₂关于参数c₂的分歧图如图5所示，当c₁取接近0的参数值时，系统失去稳定性，而增大参数值至c₂ > 3时，系统进入稳定区域。

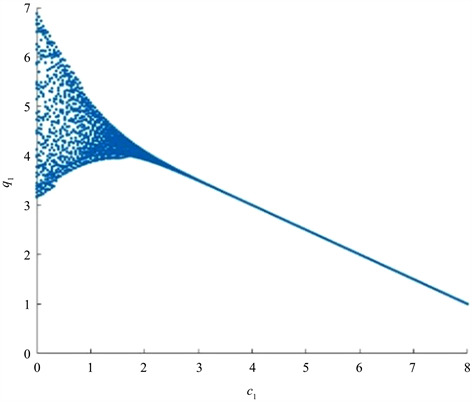
Figure 4. Image of q₁, p₂ on varying the parameter c₁

图4. q₁，p₂随参数c₁变化图像

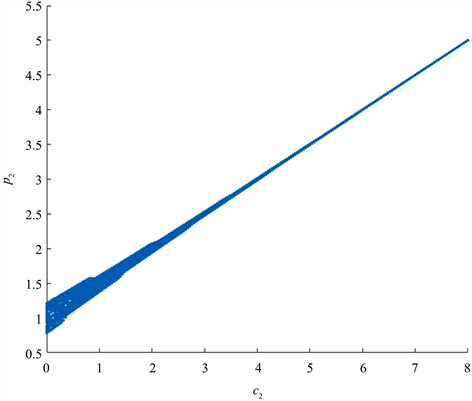
Figure 5. Image of q₁, p₂ on varying the parameter c₂

图5. q₁，p₂随参数c₂变化图像

图6显示了价格q₁的调整速度参数k₁对平衡点的影响。当其他参数分别为a = 10，b = 1，c₁ = 2，c₂ = 2，k₂ = 0.1时，从分歧图中可以观察得出，若 $k_1\in \left(0,0.1\right)$ 时，平衡点大致处稳定状态。当k₁ > 0.1时，平衡点的行为开始变得复杂而混沌。

图7显示了价格p₂的调整速度参数k₂对平衡点的影响。当其他参数分别为a = 10，b = 1，c₁ = 2，c₂ = 2，k₁ = 0.1时，从图7中可以观察得出，若 $k_2\in \left(0,0.1\right)$，平衡点失去稳定性，处于混沌状态。而随着k₂数值的增加，平衡点逐渐趋于稳定，并在考察范围内持续稳定下去。

Figure 6. Image of q₁, p₂ on varying the parameter k₁

图6. q₁，p₂随参数k₁变化图像

Figure 7. Image of q₁, p₂ on varying the parameter k₂

图7. q₁，p₂随参数k₂变化图像

4. 小结

本文研究了一类关于价格和数量竞争的混合双寡头博弈的复杂动态行为。假设每个公司在每个时间段都在有界条件下使其预期相对利润最大化，得到了一个离散动态系统的理性期望。研究了在成本函数为线性的情况下构建混合寡头博弈模型。通过对动态系统平衡点的存在性和局部稳定性的分析，利用单参数分岔图描绘了系统在其产品差异性、价格或数量调整速度等参数变化下的动力学现象。研究结果表明，企业双方价格与数量调整速度的微小变化即会对系统稳定性产生显著影响。并且，产品差异性的降低将会促使企业用提高价格的方式来提高利润，成本的增加也会诱导企业通过减少数量或提高价格的方式来提高利润。混合双寡头博弈模型的研究，在企业相对利润最大化的需求下，为其竞争策略提供了重要的理论支持。