1. 引言
随着我国经济的不断发展,越来越多民众选择乘坐飞机作为出行方式。但机场在建成后拥有的滑行道资源有限,面对日益增多的交通运输量,机场面临的压力也越来越大。虽然机场可以扩建,但当前的扩建速度远远跟不上航空运输需求的增长,并且许多机场受场地限制,导致其扩建范围十分有限。因此,在有限的滑行道资源上,提高运营效率,变得十分有必要。
对进出港航空器的滑行路径进行优化,在保证安全的前提下,缩短滑行时间,是解决当前问题的方法之一。许多学者对此做了大量的研究,并取得了一定的成果。张兆宁等人结合安全间隔、滑行规则和冲突避免限制规则,以减少滑行时间和油耗作为目标,优化滑行路径 [1]。李善梅等人提出基于变长的滑行时间窗口和A*算法结合的方法,以滑行总时间最短为目标,研究无冲突的优化路径 [2]。姜雨等人引入距离阻抗权重和转向阻抗权重因素,基于Dijkstra算法,优化航空器在滑行道上的动态调度 [3]。
以上的学者以及许多以往的学者,在研究滑行道路径优化时,大多使用的是简化的滑行道路网。这些简化的路网图将道路中转弯部分的细节省略,直接以直线段相连的方式组成路网模型,将直线段和直线段是否相连代表是否可以转弯换道。这样的处理方法,除去了实际路网中的许多细节,在某些情况下,会导致不合理的路径规划结果。
针对以上问题,本文对路网模型进行改造,加入转弯约束条件,并实现了一个改进的A*算法对新路网模型进行路径优化。在实际的工程应用中,取得了良好的效果。
2. 路网处理
在道路交通问题中,可以将路网抽象为一个图模型 [4]。图模型中每一个节点代表一个路口,每一条边代表一段道路。抽象简化的机场滑行道路网类似于图1所示。
图1中,简化的路网只能描述点的位置,以及点和点之间的连通关系。但在实际滑行道中,航空器如果需要大幅度转弯,一般有一段圆滑的弧线衔接两条大角度的路段作为缓冲。为了保存滑行道路径的更多特征,可以使用矢量数据格式存储路网数据,GeoJSON [5] 就是其中的一种。
本文中使用GeoJSON结构将滑行道路网抽象处理生成Point和Line两个数据集合,代表的图模型如图2所示。
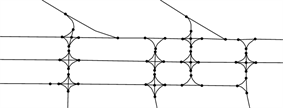
Figure 2. The road network after treatment
图2. 处理后的路网
Point集合对应每一个路口和一些重要的位置,即图2中圆点;Line集合对应每一条道路,即图2中一条条线段,每一条线段连通着两个圆点。图2中圆滑的曲线是引导航空器大幅度转弯时的缓冲弧线。最终将滑行道路网抽象处理为满足图模型的结构,并保存了道路形状信息。
3. 路径规划
3.1. A*算法
A*算法 [6] 是一种基于启发式的图搜索算法。在寻路的过程中,为每一个节点赋予一个估计值,然后选取估计值最优的节点优先遍历。估计值是使用启发式函数估算从起点经过该节点到终点的距离。启发函数如下:
(1)
其中G为起点到达当前节点的实际距离,H为从当前节点到达终点的估算距离。传统的A*算法一般使用欧式距离或者曼哈顿距离作为H的计算方法。
3.2. 加入转弯约束后的问题
依照传统A*算法的寻路方法,在下图3中搜索路径存在一定问题。

Figure 3. A simulated point-edge graph model
图3. 模拟的点边图模型
在图3中,假设路径中不能存在90度及以上的转弯处。如果搜索以A为起点,G为终点的路径。根据A*算法,搜索到F点时,从A点到F点的最短路径为A→B→D→F,但在此基础上F→G却需要转弯90度,因此该条路线不合理,导致算法无法找到合理路径。
但在图3中,可以找到从A到达G的路径A→C→E→F→G,所以根据加入的转弯约束条件,需要对A*算法进行一定改进。
3.3. A*算法的改进
在传统的A*算法中,被扩展节点记录了从起点到该节点的最优路径,但加入了转弯约束条件后,这条最短路径可能并不满足约束条件。如果将到达该节点的所有可能路径都记录的话,就没有发挥A*算法的优势。
根据滑行道的特点,将道路切换的情况可以归为下图4中的四种类型。
 (a)
(a) 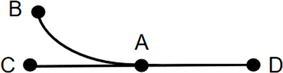 (b)
(b) 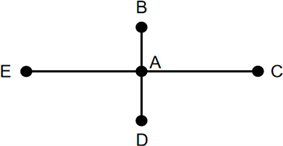 (c)
(c)  (d)
(d)
Figure 4. Road switching in taxiway
图4. 滑行道中道路切换情况
本文中,滑行道路网使用GeoJson数据结构记录了道路的形状特征,所以可以根据转弯角度,来判断是否可以转弯。
在图4的(a)中,点A与B、C相连,可以B→A→C,也可以C→A→B。因此在A点,需要将来自B、C方向的最优路径都记录,共两种情况。
在图4的(b)中,B、C都可经过A到达D,所以来自B、C方向的最优路径只需要记录为一种,加上来自D方向的最优路径,共需记录2种情况。
在图4的(c)中,因为转弯条件约束,需要点A记录四种情况:E→A→C、C→A→E、D→A→B、B→A→D。
对于图4中的(d),B、C、D都可以通过A到达E、F、G,所以扩展时,从B、C、D到达A可以视为一种情况。同理E、F、G也被视为一种情况。A点只需要记录(B/C/D)→A→(E/F/G) 和(E/F/G)→A→(B/C/D)两种情况。
A*算法改进后,同一个节点需要记录来自不同方向的最优路径,可以通过生成多个节点副本来实现。因为滑行道有其自己的特点,每个节点最多记录四种情况,所以最多生成四个副本,就可以将所有情况全部纪录。可以让每个节点都生成四个副本,也可以分析每一个节点的情况,生成对应情况数的副本数量。
3.4. 改进后A*算法的步骤
步骤如下:算法需要维护M和N两个集合,M保存哪些搜索到但还没有加入最优路径树的节点,N保存加入了最优路径树的节点。为每个节点生成四个副本。
1) 取起始节点的一个副本,初始化,并放入open中。
2) 如果M为空,则搜索失败;否则从M中选出F值最小的节点P,并将其加入N中。
3) 如果点P是终点,则结束。
4) 遍历点P相邻的可达节点:
① 检查从P点到达相邻点是否满足转弯约束。如果不满足则跳过,继续检查下一个相邻点;如果满足则进入②。
② 如果相邻点不在M和N中,则取该节点一个副本,初始化,设置父节点为点P,加入M中。
③ 如果相邻点已经在M或N中。
a. 取出M和N中的所有该节点副本,与当前情况相比较。
b. 如果相同情况存在。则在相同情况的副本中,计算通过点P到达该节点的F值是否更小。如果更小则更新F值,并将其父节点设置为点P,此时如果其在N中,则将其从N中移到M中。
c. 如果相同情况不存在。则取该节点一个副本,初始化,设置父节点为点P,加入M中。
5) 转到步骤2。
3.5. 改进后A*算法的寻路过程
在图3的基础上,仍然假设路径不能有90度及以上的转弯,但让节点记录来自不同方向的最优路径,寻路从A到G的过程如下图5所示。
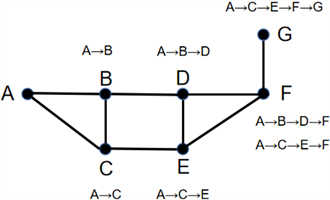
Figure 5. The improved A* algorithm pathfinding process
图5. 改进后A*算法寻路过程
图5中,在F点处,来自于D、E方向的最优路径下一步能达到的点不同。来自D方向的在F处没有下一步可达点;来自E方向的在F处下一步可达点有G。因此在F处纪录A→ B→D→F和A→C→E→F两种情况。
4. 应用实例结果
图6是一幅增加入了更多特征,更贴近实际的滑行道路网图。
引入转弯约束,在图6的基础上,使用改进的A*算法搜寻从A→G的路径。图6中粗线条路径是这次寻路的结果。从图中可以看出改进的A*算法可以成功完成路径规划,粗线条路径连通了A点和G点,并且路径曲线符合滑行道转弯约束条件。
但是,如果使用传统的A*算法或者Dijkstra算法,是无法在图6的路网图中搜索到A→G的路线,导致路径优化失败。具体情况如下。
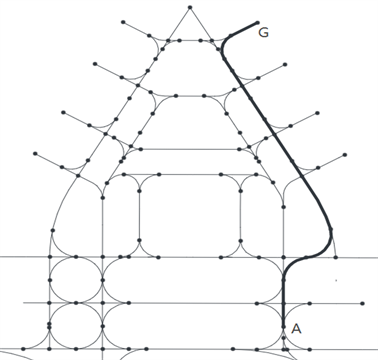
Figure 6. Pathfinding results of the improved A* algorithm
图6. 改进的A*算法的寻路结果
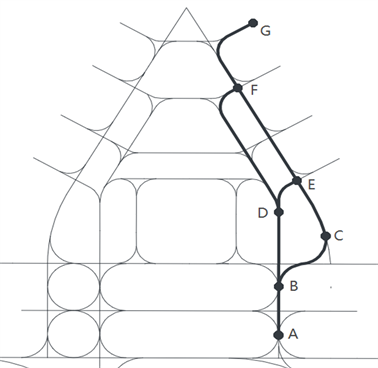
Figure 7. Path finding failure diagram
图7. 寻路失败情况图解
在图7中,传统的A*算法或者Dijkstra算法只会保存两点之间最短的一条路径。当传统算法搜索A→G路径时,在E点上,只会纪录A→B→D→E,而A→B→C→E路径因为更长而被抛弃,由于转弯条件约束,E点无法进一步E→F→G。同样的在F点处只会纪录A→B→D→F,但F无法进一步到达G点。因此传统的A*算法或Dijkstra算法在这种情况下寻路失败。
5. 结论
本文中,提出使用矢量结构GeoJSON描述滑行道特征,以更贴近实际情况的机场滑行道路网图作为寻路对象。提出在传统A*算法的基础上进行一定改进,使其满足滑行道的转弯约束条件,进而能在贴近实际的滑行道路网中进行路径规划。应用实例结果显示,改进后的A*算法能在贴近实际的滑行道路网中良好工作。本文研究结果可以为机场安全态势分析、冲突预警等方面研究提供部分的参考方案。