不同相变材料蓄热特性及液相分数无量纲准则方程式拟合

The Heat Storage Characteristics of Different Phase Change Materials and the Liquid Phase Fraction Dimensionless Criterion Equation Fitting

摘要: 主要应用数值模拟方法对三套管相变蓄热器进行研究，为该结构的蓄热器填充三种不同相变材料(RT82、RT50、LA)提供参考。拟合得到无量纲参数和液相拟合分数，其中低熔点RT50和LA平均努塞尔特数存在上升阶段；得到熔化过程中不同相变材料液相分数、不同蓄热方式的S_teF₀R_a^1/6相关函数；通过不同斯蒂芬数对所得拟合函数验证，结果表明该模型液相分数函数在S_te为0.0765~0.6060范围内适用度高；低于熔点的初温，引入初温参数S_c^1/4

Abstract: ，拟合得到液相分数的S_teF₀S_c^1/4R_a^1/6相关函数。 The main application of numerical simulation method is to study the three-tube phase change heat accumulator, which provides a reference for filling the heat accumulator with three different phase change materials (RT82, RT50, LA). Dimensionless parameters and liquid phase fitting fractions are obtained by fitting. Among them, low melting point RT50 and LA average Nusselt number have a rising stage. S_teF₀R_a^1/6 for different phase change materials and different heat storage methods during the melting process are obtained. Correlation function is verified by the fitting function and obtained by different Stephen number pairs, the results show that the liquid fraction function of the model has high applicability in the range of 0.0765~0.6060 of S_te; the initial temperature below the melting point is introduced. The temperature parameter S_c^1/4 is fitted to obtain the S_teF₀S_c^1/4R_a^1/6 correlation function of the liquid fraction.

1. 引言

相变蓄热技术是利用相变材料(Phase Change Materials, PCM)发生相变时的特点进行蓄/放热，即当PCM熔化时，直接从热源吸收能量储存，凝固时，以释放潜热的形式释放储存的能量。相变蓄热技术具有装置设计简单、蓄热密度高、蓄热温度相对恒定和易于管理等优点，具有广泛的应用前景，所以掌握相变材料蓄/放热过程中的传热规律显得越来越重要。

在相变蓄热器结构设计和优化方面，研究者多采用添加肋片的形式增强蓄/放热。如Agyenim等 [1] 通过实验方法研究了套管式蓄热器中纵向翅片和轴向翅片的蓄热性，得出了纵向肋片蓄热性能优于轴向肋片的结论。杨莺和梁艳南等 [2] 通过定量测试不同工况下管壳式蓄热器蓄热性能，发现内管传热量与管内流体温度线性增加，进一步为套管蓄热器纵向翅片设计提供了依据。李永辉等 [3] 在螺旋式蓄热器的圆管表面添加了矩形翅片，经过实验测定，蓄热时间相对光滑圆管的结构减少了1/3。Yuan等 [4] 通过数值方法研究了相变蓄热器内部纵向肋片角度设置对蓄热器蓄热性能的影响，结果表明竖直放置肋片可以更好地提高换热效率。J. Vogel等 [5] 建立了一种HTF与存储区域之间耦合瞬态热传递的模型，对特定肋片的换热特性进行了研究。Nitin Kukreja等 [6] 研究了壳内融化的螺旋管式相变蓄热器，探究了不同的进口水温对蓄热效率的影响。Jasim Abdulateef等 [7] 研究无翅片管LHSU，纵向翅片管和圆形翅片管的蓄热性能，后两者的总蓄热时间分别减少了69%和55%，实验表明圆形翅片管的带电热负荷运行性能提高了2.1倍。Xiaoling Cao等 [8] 从入口温度，质量流量和相变温度对传热过程的影响研究了三套管蓄热器，赵明等 [9] 研究发现安装分形肋片的相变蓄热器可使蓄、放热时间缩短，可逆性更好，换热效率更高，为本文研究采取内部纵向肋片的三套管蓄热器提供了依据。

因为相变材料自身的导热系数较低，为改进相变材料性质，研究者多对相变材料进行合成改良，如部分科研人员选择用石墨作为相变材料的定型材料进行合成，如高丽媛等 [10] 在石蜡中分别添加不同体积分数的纳米石墨烯和纳米石墨烯片，通过两步法制备纳米颗粒复合相变材料，结果表明，对于导热为主导的凝固过程，复合相变材料的凝固速率相对于纯石蜡有提升作用；对于融化过程，导热和对流共同作用决定融化速率是否被强化。赵思勰等 [11] 采用熔融共混法制备了癸酸/膨胀石墨定型相变材料(DA/EG-PCMs)、月桂酸/膨胀石墨定型相变材料(LA/EG-PCMs)和石蜡/膨胀石墨定型相变材料(PA/EG-PCMs)，发现在膨胀石墨的高导热网络结构包覆下，三种膨胀石墨基定型相变材料相变温度提前，耐久性提高，提高了PA/EG-PCMs热稳定性。李云涛等 [12] 以膨胀石墨(EG)为载体，石蜡为相变材料，利用EG对石蜡良好的吸附性，制备了膨胀石墨基复合相变材料，经过测试表明，EG的质量分数应控制在10%左右能保证相变材料的结构稳定和优良性能。蒋自鹏，铁生年 [13] 以复合芒硝(SCNa)为相变材料，膨胀石墨为载体，采用真空吸附法制备出导热增强型膨胀石墨/复合Na₂SO₄·10H₂O定形相变材料。试验结果表明：表面活性剂OP-10 (质量分数5%)的加入能有效提高膨胀石墨和复合Na₂SO₄·10H₂O相变材料的结合稳定性，表面活性剂的添加对定形相变材料导热系数基本无影响，添加表面活性剂的膨胀石墨定形相变材料导热系数为原材料的215%。Ming Liu等 [14] 将无机盐PCM放入多孔材料形成稳定的PCM，发现孔隙率从底部到顶部的增加，熔融过程可以进一步加速，在下部腔体插入导热增强剂更有效。

部分国内科学家采用多种相变材料制成混合相变材料，如王学晨等 [15] 以正二十烷、聚乙烯和乙丙橡胶等为原料经熔融挤出，制成正二十烷含量10%~65%的共混切粒。以正十八烷微胶囊和聚乙烯为原料经熔融挤出，制成微胶囊含量10%~60%的共混切粒。切粒的热焓随相变材料含量的增高而增大。切粒的熔融指数随相变材料或相变材料微胶囊添加量的增高呈现指数增大或反S曲线的形式。

本文采用三种不同相变材料分别为：月桂酸(LA)、氯化石蜡RT85和RT50填充在具有内部纵向肋片的三套管蓄热器中，主要研究该三种相变材料的蓄热特性，并考虑不同蓄热方式、斯蒂芬数和初温参数在蓄热性能方面的影响，拟合得到液相分数的无量纲准则方程式。

2. 物理模型和数学模型

2.1. 物理模型

该物理模型1简图如图1所示，三套管式蓄热器内部圆直径为50 mm，相变材料区域直径为150 mm，设备整体直径为200 mm。其中模型1为内部相变材料区域安装厚度1 mm、长度42 mm的导热肋片，与文献 [16] 一致。

Figure 1. Model 1 structure diagram

图1. 模型1结构简图

2.2. 数学模型

对于融化后的PCM流体区域引入无量纲参数进行分析。其中热扩散系数α为K/(ρ·C_p)，Δt为计算时间，D为当量直径D_m-D_in，K为相变材料的导热系数，ρ即通过变物性方程根据平均温度计算得到PCM流体平均密度，C_p为PCM定压比热容。

格拉晓夫数G_r定义为：

$G_r=\frac{g\beta \left(T_w-T_m\right)D^3}{v^2}$ (1)

其中g为重力加速度9.81 m/s²，β为PCM体积热膨胀系数，T_m为PCM相变温度，ν为运动粘度。

瑞利数R_a定义为：

$R_a=P_r\cdot G_r$ (2)

其中普朗特数P_r为ν/α。

对于PCM区域对流换热引入平均努赛尔数 $\overline{Nu}$，定义如下：

$\overline{Nu}=\frac{\bar{h}\cdot D}{k}$ (3)

其中 $\bar{h}$ 为PCM材料液相流体的平均对流传热系数。

2.3. 数值计算方法和模型考核

2.3.1. 数值计算方法

采用ANSYS Fluent中融化凝固模型进行数值计算工作，该模型利用焓法模型，其中将相变材料的糊状区视为多孔介质，并设孔隙率与液相分数相等。对于固相孔隙率为零且速度为零。对于糊状区，由于糊状区孔隙率会不断地减少，从而引起动量的下降。Fluent中融化凝固模型能够模拟大部分融化凝固现象，包括融化、凝固、结晶、晶体生长和连续铸造等问题。此外，速度与压力采用SIMPLEC算法，压力项采用PRESTO方法离散，对流项采用QUICK格式离散，能量为一阶迎风格式。压力、密度、速度、液相分数、能量亚松弛因子分别设为0.3、0.5、0.3、0.9和0.6。求解时间步长为0.5 s。

2.3.2. 模拟方法验证

为了验证本文数值计算方法的正确性，模型1的计算结果对文献 [16] 中实验结果进行对比。模拟结果如图2所示。

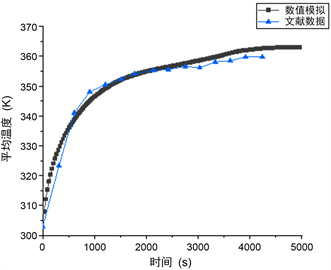
Figure 2. Comparison of numerical simulation results and literature data

图2. 数值模拟结果和文献数据对比

由图2可知，蓄热工况时，数据相差3.97%。由此可知，本文采用模型准确可靠，可以利用该模拟方法对三套管相变蓄热换热器进行模拟研究。

2.3.3. 物性条件

1) 相变材料相变过程中采用层流模型，为低速非稳态不可压流动过程；

2) 相变材料和管壁材料为均质和各向同性；

3) 不考虑粘性耗散，密度采用Boussinesq假设，物性参数如表1：

Table 1. Physical property parameter table

表1. 物性参数表

3. 不同相变材料的蓄热特性

3.1. RT82、RT50、LA相变材料的蓄热特性

为研究RT82、RT50、LA材料在三套管蓄热器中融化过程，分别计算相变材料区域平均温度和液相分数。计算结果如图3所示。

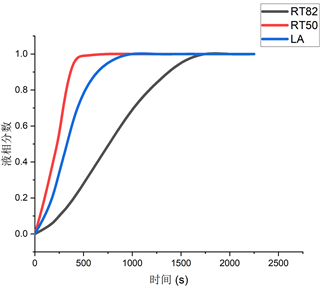(a) 液相分数 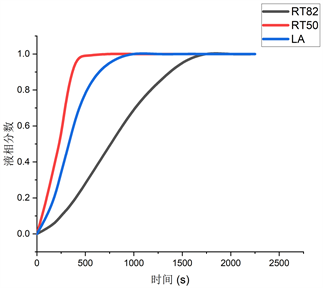(b) 平均温度

Figure 3. RT82, RT50, LA melting process

图3. RT82、RT50、LA融化过程

如图3(b)可知，RT82材料在加热温度为90℃边界条件下的平均温度变化曲线，由于RT82材料熔点在350.15 K到358.15 K之间，材料区域在加热至1000 s后平均温度变化减小，并且逐渐接近与363.15 K。由图3(a)可知，RT82材料在加热至1800 s左右融化完毕。

如图3可知，RT50由于熔点相对于RT82材料较低，同样在T_w为363.15 K条件下，迅速融化。整体完全融化时间为400 s。R_a最大值为3.88 × 10⁸，G_r最大值为7.3 × 10⁶，液态相变材料的对流属于层流。

如图3可知，由于LA材料熔点为317.15 K，在T_w = 363.15 K的条件下融化迅速，在750 s时接近壁面加热温度363.15 K，导致换热强度减弱，温度变化减缓。随着温度不断升高，整体完全融化所需时间为800 s，大于RT50但小于RT82。R_a最大值为6.08 × 10⁸，G_r最大值为7.28 × 10⁶，属于层流。

3.2. 液相对流对蓄热特性的影响

相变材料区域无量纲参数统计结果如图4所示。

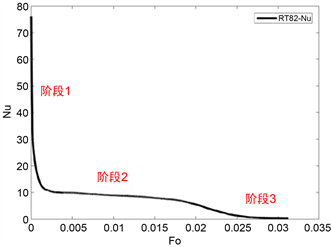(a) RT82 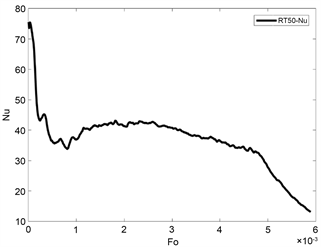(b) RT50 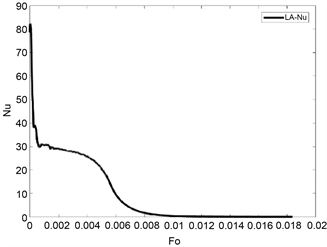(c) LA

Figure 4. $\overline{Nu}$ change of Phase change material heat storage process graph

图4. 相变材料蓄热过程 $\overline{Nu}$ 变化图

由图4(a)可知，在以F_o为时间变化参数的加热过程中， $\overline{Nu}$ 在变化过程中分为三个阶段。在初期阶段1，通过融化而产生了对流换热强度较高RT82液相薄层，此时 $\overline{Nu}$ 数值较高。随着温度不断升高，PCM不断融化，所形成的薄层逐渐变厚，此时对流换热强度急速下降。在中期阶段2，由于液相RT82大量产生，温度变化相对较大， $\overline{Nu}$ 不再减小，小幅增加后趋于平缓，此时对流换热强度仍占主导地位。后期阶段3由于温度变化趋于平缓，蓄热器存在部分PCM难以融化的情况，传热过程以对流换热强度迅速下降。当温度接近加热壁面温度时， $\overline{Nu}$ 趋近于0。其中，计算结果R_a最大值为1.26 × 10⁷，G_r最大值为3.6 × 10⁴，表明PCM自然对流为层流，符合假设。

由图4(b)可知，RT50的 $\overline{Nu}$ 变化与RT82相同，分为三个阶段。而RT50的变化波动较大，其中阶段2存在 $\overline{Nu}$ 变化存在上升区间。这是由于RT50的熔点较低，在相同温度边界条件下对流换热效应更大。在第2阶段中，大量的液相RT50生成提高该阶段前期的自然对流强度，第二阶段的对流强度相较其他两种相变材料较高。

如图4(c)所示， $\overline{Nu}$ 变化与RT82相同，分为三个阶段。其中第2阶段与RT50材料相同存在上升区间。由于LA材料熔点最低，融化最快，因此其 $\overline{Nu}$ 第2阶段时间最短。

综上所述，三种PCM在三套管蓄热器模型融化过程中，液态材料首先产生于加热面和金属肋片附近形成，此时自然对流效应最强。随着温度升高，液相增多的同时，自然对流强度迅速减小。随后在一定范围内小幅增长后稳定，最终随着整体温度接近壁面不断降低。受相变温度影响，三种材料融化速率不同，其中RT50完全融化所需时间最短，RT82最长。根据R_a、G_r计算结果流体流动均为层流。

4. 液相分数的无量纲准则方程式拟合

4.1. 不同相变材料液相分数拟合

由不同PCM蓄热过程的液相分数变化可知，三套管模型中相变材料的融化具有相同的融化阶段。为研究PCM液相分数的变化特性，引入无量纲参数斯蒂芬数S_te。

其中斯蒂芬数S_te定义为：

$S_{te}=\frac{C_p\left(T_w-T_m\right)}{L}$ (4)

C_pl为液态比热容，L为相变材料的相变潜热值，T_m为PCM的相变温度，T_w为加热表面温度。PCM液相分是函数f与无量纲参数S_te、F_o、R_a相关，其中定义变量x为 $S_{te}{F}_o{R}_a^{\frac{1}{6}}$。

将x与液相分数拟合，结果如图5所示。

Figure 5. x Fitting with liquid fraction

图5. x与液相分数拟合

根据图5可知，不同PCM的液相分数与变量x具有较强联系性。由于PCM液相分数具有从0到接近1的变化趋势，因此采用Rayleigh曲线模型，根据三条曲线数据拟合得到f方程：

$f=1-{\text{e}}^{\frac{-{\left(\frac{X}{0.0217}\right)}^2}{2}}$ (5)

其中x为 $S_{te}{F}_o{R}_a^{\frac{1}{6}}$。 $0.1478\le S_{te}\le 0.606$， $2.14\times {10}^7\le R_a\le 6.09\times {10}^8$。方程相关系数R²为0.99996，拟合程度非常高。

4.2. 不同蓄热方式液相分数拟合

基于上述部分可知通过三套管内外壁面加热可使PCM迅速融化，模型实际使用过程中，由于内外管采用独立的流速控制，因此可以采用单独的加热方式。其中边界条件为：

1) 只有内部加热： $T_w=T_{in}=363.15\text{K}$， $R=R_m$ ： $q=0$

2) 只有外部加热： $T_w=T_{out}=363.15\text{K}$， $R=R_m$ ： $q=0$

在初始温度为300.15 K的工况下分别统计不同蓄热方式的液相分数变化。结果如图6所示。

由图6可知，由于三套管蓄热器外壁面接触面积大于内部面，因此单独采用外壁面加热比单独采用内壁面具有更高的蓄热效率。内外壁面同时加热的情况下蓄热效率为最高。因此，针对三套管蓄热器不同蓄热方式的液相分数变化分别拟合。

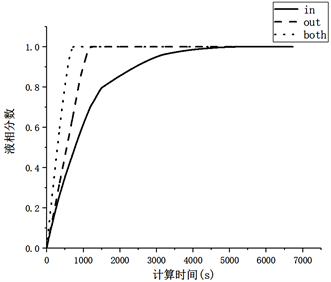
Figure 6. Liquid fraction of different heat storage methods

图6. 不同蓄热方式的液相分数

其中内部壁面蓄热方式的液相分数拟合结果如图7所示。

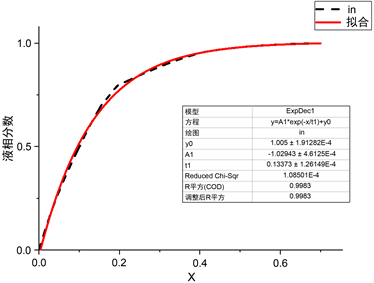
Figure 7. Fitting results of liquid phase fraction of the internal heat storage method

图7. 内部壁面蓄热方式液相分数拟合结果

由图7可知，对于内管单独加热情况，采用液相分数f_in与变量x的拟合函数如下：

$f=1-1.03{\text{e}}^{\frac{-x}{0.134}}$ (6)

相关系数R²为0.9983。其中 $x=S_{te}{F}_o{R}_a^{\frac{1}{6}}$， $S_{te}=0.606$， $7.2\times {10}^7\le R_a\le 7.7\times {10}^7$。

外部壁面蓄热方式的液相分数拟合结果如图8所示。

Figure 8. Fitting results of liquid fraction of external wall heat storage method

图8. 外部壁面蓄热方式液相分数拟合结果

由图8可知，对于外管单独加热情况，液相分数f与变量x的拟合函数如下：

$f=1-{\text{e}}^{\frac{-{\left(\frac{x}{0.0573}\right)}^2}{2}}$ (7)

其中相关系数R²为0.9964。其中 $x=S_{te}{F}_o{R}_a^{\frac{1}{6}}$， $S_{te}=0.606$， $7.4\times {10}^7\le R_a\le 7.7\times {10}^7$。

4.3. 不同斯蒂芬数对拟合函数的影响

在三套管式相变蓄热器中，为进一步研究S_te对该模型的蓄热性能的影响，在填充LA材料时，加热

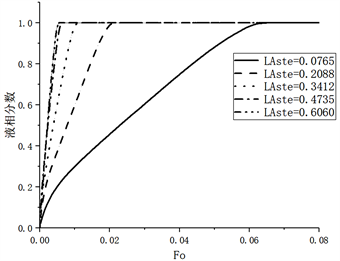
Figure 9. Variation of liquid fraction fractions with different Stephen numbers

图9. 不同斯蒂芬数的液相分数拜变化

温度分别选取为50℃、60℃、70℃、80℃、90℃。其对应的斯蒂芬数分别为0.0765、0.2088、0.3412、0.4735、0.6060，液相分数统计结果如图9所示。

如图9可知，在0.0765~0.6060的区间内，斯蒂芬数对相变材料的融化速率影响较大，因此可以通过增加斯蒂芬数来提高LA材料融化速率。但从图9同样可看出，虽然增加斯蒂芬数在某个范围内可以迅速增加熔化速率，但斯蒂芬数到达某个数值后，熔化速率并没有很大改变，对应的斯蒂芬数从0.4735增加到0.6058时，熔化速率并未有明显提高，说明加热温度并非愈高愈好。

带入不同斯蒂芬数的x与液相分数拟合公式(5)计算，计算结果如图10所示。

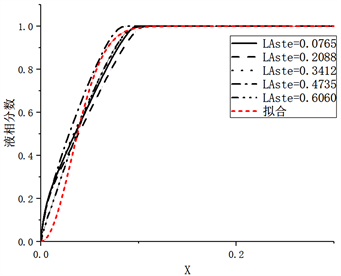
Figure 10. Liquid phase fraction fitting with different Stephen numbers

图10. 不同斯蒂芬数的液相分数拟合

如图10可知，液相分数的无量纲准则方程式f在不同S_te条件下所得的液相分数变化数据具有良好相关性，因此0.0765~0.6060的范围内具有良好的适用性。R_a数变化范围为7.7 × 10⁷~6.1 × 10⁸。

4.4. 不同初温参数对拟合函数的影响

由于三套管模型在实际使用中存在不同的初始温度，因此引入低于熔点的初温参数定义如下：

$S_c=\frac{C_p\left(T_m-T_{init}\right)}{L}$ (8)

C_p为比热容，L为相变材料的相变潜热值，T_m为PCM的相变温度，T_init为初始温度。

初始温度280.15 K、285.15 K、290.15 K、295.15 K、300.15 K对应S_c参数为。0.2279、0.2941、0.3602、0.4264、0.4926。

分别模拟LA材料不同初温下的液相分数变化，模拟结果如图11所示。

由图11可知，不同的初始温度导致蓄热器PCM液相分数在融化后期变化较大，其中T_init越低，PCM完全融化时间越长。这是由于更低初始温度需要吸收更多的热量才能达到相变温度。

考虑初温参数对液相分数的无量纲准则方程式的影响，在因变量x中加入 $S_c^{-\frac{1}{4}}$ 参数，即 $x=S_{te}{F}_o{S}_c^{-\frac{1}{4}}{R}_a^{\frac{1}{6}}$。将x与液相分数进行拟合。拟合结果如图12所示。

由图12可知，不同S_c计算所得x与对应的液相分数吻合度很高。根据数据拟合函数为：

$f=1-{\text{e}}^{\frac{-{\left(\frac{x}{0.04756}\right)}^2}{2}}$ (9)

其中 $S_{te}=0.606$， $5.64\times {10}^8\le R_a\le 6.09\times {10}^8$， $0.2279\le S_c\le 0.4926$。

相关系数R²为0.9795。由表可知，函数与数据相关性较高。

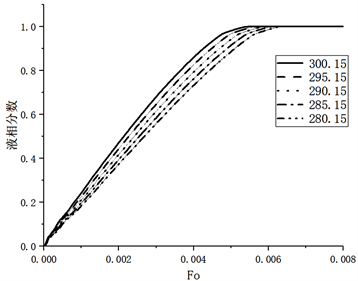
Figure 11. Liquid fraction of LA materials at different initial temperatures

图11. 不同初温LA材料液相分数

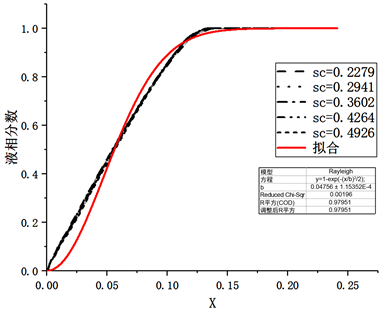
Figure 12. Fitting results of different S_c parameters

图12. 不同S_c参数拟合结果

5. 结论

本文通过数值方法建立了三套管相变蓄热换热器模型，研究了三种不同熔点的相变材料(LA、RT50和RT82)的蓄热特性，获得了如下结论：

1) 不同熔点的相变材料虽然自然对流强度变化存在较大差异，但存在相似的熔化阶段。

2) 对不同相变材料、内外管不同蓄热方式、不同蓄热温度拟合得到不同相变材料熔化过程的液相分数相关函数(自变量x为 $S_{te}{F}_o{R}_a^{\frac{1}{6}}$ )，函数准确度较好，可以预测在该模型内相变材料的液相分数变化。

3) 考虑低于熔点的初温参数对蓄热器模型的影响，通过引入初温参数 $S_c^{-\frac{1}{4}}$，进过拟合得到液相分数与 $S_{te}{F}_o{S}_c^{-\frac{1}{4}}{R}_a^{\frac{1}{6}}$ 相关函数，可用于预测。

基金项目

国家自然科学基金NO. 51306120。