小区开放对道路通行的影响

The Influence of Community Opening on Road Passage

摘要: 针对2016年国务院发布的《关于进一步加强城市规划建设管理工作的若干意见》，考虑将已建成的住宅小区逐步开放。在小区开放后形成的丁字交叉口和十字交叉口处，加设信号灯，且相邻交叉口进行动态协调相位控制，从而达到优化路网结构，提高道路通行能力，改善交通状况的目的。基于现有的数据，依据筛选典型指标法，建立相关系数矩阵，从起始六个初定指标中，筛选出车辆时间延误和通行能力作为最佳的评价指标，建立评价指标体系。通过分析小区开放对周边道路的车流量、信号灯周期时长、相位差、绿信比及红、黄、绿灯期间的消散量的影响，建立相邻信号交叉路口控制系统的双目标动态优化模型。以时间延误为主要目标，总消散量为次要目标，基于分层序列法求解该模型。以B类城市的中型小区作为研究对象，建立实际通行能力计算模型。通过建立Greenshields速度–密度关系模型，得到不同路段和不同结构的小区，在开放前后的自由流速度，得知小区开放产生的效果与小区结构、周边道路结构及车流量有关。通过改进车辆通行模型中关于车流量的计算公式，对于各类型小区，定量比较其开放前后的时间延误和通行能力。结果表明，小型小区开放后对周边道路通行有反向作用，而中型和大型小区开放后对周边道路通行有正向作用。二岔口开放式小区比封闭式小区的通行能力提高了1.24%，平均每小时多通行24辆车。采用现实中某小区的参数，对模型进行验证，验证结果与理论值契合，说明模型是切实可行的。最后，将引进仿真模拟对模型进行改进。

Abstract: In response to the “Several Opinions on Further Strengthening the Management of Urban Planning and Construction” issued by the State Council in 2016, it is considered to gradually open up the completed residential communities. At the T-shaped intersections and cross intersections formed after the opening of the community, signal lights are added, and adjacent intersections are dynamically coordinated and phase controlled, so as to optimize the road network structure, improve road capacity, and improve traffic conditions. Based on the existing data, the correlation coefficient matrix is established according to the screening of typical indicators. From the initial six initial indicators, the vehicle time delay and capacity are selected as the best evaluation indicators, and the evaluation index system is established. By analyzing the influence of community opening on the traffic volume, signal lamp cycle duration, phase difference, green signal ratio, and the amount of dissipation during red, yellow, and green light periods, a dual-objective dynamic optimization model of the adjacent signalized intersection control system is established. Taking time delay as the main objective and total dissipation as the secondary objective, the model is solved based on the layered sequence method. Taking the medium-sized communities in Class B cities as the research objects, the actual capacity calculation model is established. Through the establishment of the Greenshields speed-density relationship model, the free flow speeds of different road sections and different structures are obtained before and after the opening, and it is known that the effect of the opening of the district is related to the structure of the district, the surrounding road structure and the traffic flow. By improving the calculation formula of vehicle flow in the vehicle traffic model, for each type of community, the time delay and traffic capacity before and after opening are quantitatively compared. The results show that the opening of small communities has a negative effect on the surrounding roads, while the medium and large communities have a positive effect on the surrounding roads. The traffic capacity of the Erchakou open community is 1.24% higher than that of the closed community, with an average of 24 more vehicles per hour. Using the parameters of a certain community in reality, the model is verified, and the verification results are consistent with the theoretical values, indicating that the model is feasible.

1. 引言

针对国务院发布的《关于进一步加强城市规划建设管理工作的若干意见》，提出开放小区能否达到优化路网结构，提高道路通行能力，改善交通状况以及改善效果如何的问题，探究小区开放对周边道路通行的影响。

2. 符号的说明

3. 模型的准备

3.1. 收集数据

1) 根据中华人民共和国建设部《城市居住规划设计规范》 [1] 中，我们可大致取各类型小区占地面积如下：

小型：90 × 90平方米；

中型：280 × 280平方米；

大型：600 × 600平方米。

各类型小区中，分别有多少户人家：

小型：户数300~1000户或人数1000~3000人规模。

中型：户数3000~5000户或人数10000~15000人规模。

大型：户数10000~16000户或人数30000~50000人规模。

2) 根据《各种道路设计以及规定汇总》文库 [2] 中，得到：

城市主干道路(两信号灯之间)长度为：[900 − 150, 900 + 150]，单位：米。

3) 以下为某B类城市，两个时段，四种不同类型的汽车，在城市主干道路上，通过的数量。见表1。单位：辆。

Table 1. The number of different vehicle types passed at this point in time

表1. 不同车型在该时间点通过的数量

4) 据文献 [1]，以下为主干道平均车速，即建成区主干道上机动车的平均行程速度。见表2。单位：公里/小时。

Table 2. Main road average speed classification table

表2. 主干道平均车速分级表

5) 运用系统抽样调查某小区，调查结果表明，平均小区每户有三口人(爸爸、妈妈、孩子)，平均每户有一辆车、一辆电动车、一辆自行车(本次研究，将电动车和自行车同视为非机动车)，且每天早上7~8点为上班高峰期，调查结果表明，该小区住户人口中90%的机动车，在上班高峰期都会离开小区，80%的非机动车在上班高峰期会离开小区。

3.2. 数据的预处理

以上数据1) 2) 4)来源于网络资源，属于二手数据，该数据原则上认为可靠3) 5)数据来源于实地考察，利用系统抽样法，进行概率抽样。

早上7~8点的城市主干道路上的车辆通过：

首先将一小时分为六份，一份10分钟，掷筛子选出一个随机数字为2，依次取7:02, 7:12, 7:22, 7:32, 7:42, 7:52共六分钟，实地测算每分钟各车型的通行量。从而得到总的通过量。

抽样误差分析 [3]：

小型汽车的车辆通过量占总通行量大概是30%，那么大部分的样本结果会落在27.2%~32.8%之间。以总体真值30%为中心，有95%的样本结果在±2.8%的误差范围内波动，也就是30% − 2.8% = 27.2%，30% + 2.8% = 32.8%。这个±2.8%的误差是由抽样的随机性带来的，即为系统抽样的抽样误差。

样本量： $432+56+18+838=1344$

小轿车误差浮动范围为： $1344\times 27.2\%=356.568$

$1344\times 32.8\%=440.832$

而实际测量值为 $432\in \left[356.568,440.832\right]$，见图1，该数据经过误差分析，在误差范围内，认为该数据真实可靠。

Figure 1. Error analysis diagram

图1. 误差分析图

4. 模型的建立与求解

4.1. 建立评价指标体系模型

在评价指标体系中，取通行能力、排队长度、时间延误、行程时间、交通符合度、行程延误等评价指标。基于中华人民共和国道路交通安全法 [4]，通过问卷调查了解人们对道路通行影响的比重。调查结果见表3所示：

Table 3. Questionnaire survey results of road traffic indicators

表3. 道路通行指标问卷调查结果

采用筛选典型指标法，将所选择的六项指标进行筛选，得出适合具有评价体系的指标。

将表中的数据构成4 × 6矩阵，记矩阵A，通过SPSS软件求得矩阵A的相关系数矩阵 [5] $\xi$

$\xi =\left[\begin{array}{cccccc}1& 0.963& 0.586& 0.970& 0.796& 0.781\\ 0.963& 1& 0.763& 0.997& 0.927& 0.921\\ 0.586& 0.763& 1& 0.751& 0.950& 0.948\\ 0.970& 0.997& 0.751& 1& 0.919& 0.905\\ 0.796& 0.927& 0.950& 0.919& 1& 0.996\\ 0.781& 0.921& 0.948& 0.905& 0.996& 1\end{array}\right]$,

计算指标与其它指标之间的相关系数的平方 $r_i^2$

$r_i^2=\frac{1}{n-1}\left({\displaystyle \underset{j=1}{\overset{1}{\sum }}{r}_{ij}^2-1}\right),n=1,2,\cdots ,n$

$r_i^2$ 能够反映出矩阵A中各元素之间的关系程度，在此我们定义阈值条件：当 $r_i^2>0.05$ 时，认为该项能做为评价指标。

通过Matlab [6] 程序可解得其相关系数 [7] 的平方为：

$r_i^2=\left\{0.05820.04750.06110.04810.04720.0480\right\}$

因此选取通行能力和延误时间 [8] 作为评价指标。

假设小区附近主干道行驶车辆数是最大通行量，假设小区附近的车辆依次有序的通过主干道。

对于封闭小区：

令小区附近主干道速度为v₁ (km/h)，主干道上的车依次按照车辆行驶安全距离通过主干道，安全行驶距离为d₁ (m)。

可算出一小时车辆行驶的距离：

$D_1=v_1\times 1\left(\text{km}\right)$, (1)

在该时间能主干道行驶的车辆：

$N_1=\frac{D_1}{d_1}\left(\text{pcu}\right)$, (2)

通行能力为：

$S_1=\frac{N_1}{T}\left(\text{pcu}/\text{h}\right)$ (3)

同理对于开放小区：

令小区附近主干道速度为v₂ (km/h)，主干道上的车依次按照车辆行驶安全距离通过主干道，安全行驶距离为d₂ (m)。

可算出一小时车辆行驶的距离：

$D_2=v_2\times 1\left(\text{km}\right)$, (4)

在该时间能主干道行驶的车辆：

$N_2=\frac{D_2}{d_2}\left(\text{pcu}\right)$, (5)

通行能力为：

$S_2=\frac{N_2}{T}\left(\text{pcu}/\text{h}\right)$ (6)

为了研究具有代表性，所选取B类城市为研究对象。下表为各类城市和道路评价等级所对应的小区主干道平均速度分级表，见表4：

Table 4. Main road average speed classification table

表4. 主干道平均车速分级表

选择选择B类城市中道路评价等级为一级附近的小区进行研究，由表1可知其主干道平均车速为[31, 36]。用Excel在[31, 36]中随机产生1000个数据，产生数据的平均数为封闭小区附近主干道路的平均速度 $v_1$，产生随机数据详见支撑材料。小区开放后主干道上部分车驶入小区道路，使得主干道上车辆减小，车速必然加快。故可用Excel在[33, 36]中随机产生1000个数据，同样生成数据的平均数作为开放小区附近主干道路的平均速度 $v_2$，据详见支撑材料。得出 $v_1\approx 33.49\left(\text{km}/\text{h}\right)$， $v_2\approx 34.53\left(\text{km}/\text{h}\right)$。

根据《中华人民共和国道路交通安全法》 [4] 中可知城市道路车辆行驶速度在30~50 km/h时两车安全行驶距离为30~50 m左右，但由观测勘察得到，实际车辆行驶距离大约为30 m。所以取 $d_1=d_2=30\text{m}$ 根据《各种道路设计以及规定汇总》，了解主干道路长度为：[1050, 750]，为了方便计算取主干道路长度 $L=1000$。

由Matlab编程可计算得：

$S_1=1116辆/\text{h},S_2=1151辆/\text{h}$

令f₁代表主干道上的交通流， $v_a\left(f_1\right)$ 代表交通流为f₁时路段的车流速度，L代表主干道路的长度，ψ表示通过主干道的消耗时间之比，即用主干道的信号控制总延误除以主干道的等待和消散的车辆数得ψ，

所以通过主干道路所用时间为： $t=\frac{L}{v_a\left(f_1\right)}+\psi$

小区封闭时通过主干道的时间： $t_1=\frac{L}{v_{a1}\left(f_1\right)}+{\psi }_1$

小区开放后通过主干道的时间： $t_2=\frac{L}{v_{a2}\left(f_1\right)}+{\psi }_2$

$\Delta t=t_1-t_2=\left(\frac{L}{v_{a1}\left(f_1\right)}+{\psi }_1\right)-\left(\frac{L}{v_{a2}\left(f_1\right)}+{\psi }_2\right)$

由 $\psi$ 的表达式可知， ${\psi }_1,{\psi }_2$ 相差不大，

故 $\Delta t\approx \frac{L}{v_{a1}\left(f_1\right)}-\frac{L}{v_{a2}\left(f_1\right)}$ (其中 $v_{a1}\left(f_1\right)=v_1$， $v_{a2}\left(f_1\right)=v_2$ )，

由MATLAB编程可解得 $\Delta t=3.237(\; s\; )$

由上数据可得：

$S_1<S_2,t_1>t_2$

所以小区开放后主干道路的通行能力增强，时间延缓减小。故选取通行能力和时间延误做为的评价指标合理。

4.2. 建立关于车辆通行的数学模型

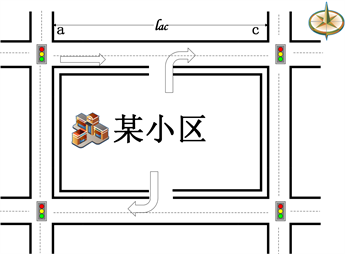
当小区为封闭式时，l路段为一条直行单向单行车道；当小区为开放式时，首先认为该小区可开辟一条支路如图2(B)，则l路段与该小区中间的支路形成一个丁字路口，为了该丁字路口的安全起见，应设置信号灯来指示车辆通行，所以，在i处设置一个信号灯。接下来，本文选定l路段作为研究对象，通过分析l路段在小区开放前后的通行能力及车辆时间延误，来研究小区开放对周边道路通行的影响。

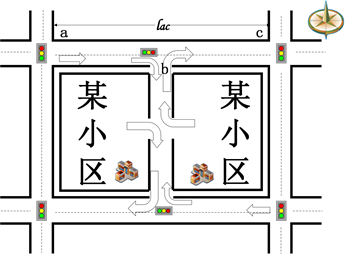(A) (B)

Figure 2. (A) Closed; (B) Open two forks

图2. (A) 封闭式；(B) 开放式二岔口

4.2.1. 建立相邻信号交叉路口控制系统的动态优化模型

见图2(A)和图2(B)，城市道路中相邻信号交叉路口a，b，c，封闭式小区为a，c相邻的主干道路，开放式小区为a，b，c相邻的主干道路，该路段长为 $l_{ac}$，令 $t_i$ 作为i信号交叉路口的周期时长，令 $k_i$ 为i交叉路口信号相位集(其中， $i\in \left(\text{a},\text{b},\text{c}\right)$ )， $\varnothing$ 作为交叉路口的东、西、南、北入口的集合， $\varnothing =\left\{\phi |e,w,s,n\right\}$，交叉路口的左转、右转、直行建立集合 $\omega =\left\{\theta |z,y,l\right\}$， $k_{i\phi \theta }$ 为控制交叉路口相位，且 ${\alpha }_{i\phi \theta }$ 为 $k_{i\phi \theta }$ 相位的绿信比(其中， $\phi$ 为入口， $\theta$ 为方向)。该绿信比应满足条件为：

${\displaystyle \underset{\phi \in \varnothing }{\sum }{\displaystyle \underset{\theta \in \omega }{\sum }{\alpha }_{i\phi \theta }}}\le 1$

本文以相邻信号交叉路口为协调控制系统，协调相位为东、西方向直行，协调路口为b处的丁字路口和c处的十字路口。令 ${\Delta }_{bc}^n$ 作为交叉路口b和c在第n周期协调相位的相位差。

在研究过程中，若固定周期时长，虽然有利于控制系统的操作，但只适用于车流较小的时候，不适用于车流较大的时候，因此可以允许周期时长在一定范围内波动，期间必须要求车辆和行人安全通过交叉路口且充分利用绿灯信号时间，则该周期时长范围可以规定为：

$t_{\min }<t_i<t_{\max }$,

其中 $t_{\min }$ 为信号周期时长的下限， $t_{\max }$ 为信号周期时长的上限。

1) 车辆的时间延误

令 $v_{\theta }$ 为 $\theta$ 方向车流，在绿灯期间的车辆消散速度，

令 $p_{c\phi \theta }\left(t\right)$ 为在c交叉路口上， $\phi$ 入口 $\theta$ 方向在t时刻的车辆到达率，

令 $q_{c\phi \theta s}$ 为在c交叉路口上， $\phi$ 入口 $\theta$ 方向上消散剩余车流量(其中，s表示消散剩余)，则消散量为：

$q_{c\phi \theta }^n=\min \left\{v_{\theta }{\alpha }_{i\phi \theta }{t}_i,q_{c\phi \theta s}^{n-1}+{\displaystyle {\int }_0^{t_i}{p}_{c\phi \theta }\left(t\right)\text{d}t}\right\}$ (7)

进入l路段的车流分别有：小区中间的支路开出的车流；从a路口沿着l路段开出的车流；c路口上一次信号灯结束后消散剩余的车辆。

因此，在第n周期，路段 $l_{bc}$ 路段上直行的车流由两部分组成：第n-1周期消散剩余的车辆，以及第n周期由b交叉路口进入路段 $l_{bc}$ 直行的车辆,则受b路口和c路口的协调相位控制的 $l_{bc}$ 路段的车流量为：

$q_{cwz}^n=q_{cwzs}^{n-1}+P_{bwz}{q}_{bwz}^n+P_{bsy}{q}_{bsy}^n$ (8)

式中， $P_{bwz}$ 表示车辆在b交叉口西入口选择直行的车辆比例， $P_{bsy}$ 表示车辆在b交叉口南入口选择向右行驶的车辆比例。

第n周期，b交叉路口对c交叉路口的协调相位红灯和黄灯期间累计到达的车流量为：

$q_{cwzm}^n={\displaystyle {\int }_0^{\left(1-{\alpha }_{cwz}\right)t_i}{q}_{cwz}\left(t\right)\text{d}t}$ (9)

其中，m表示红灯和黄灯期间， $q_{cwz}\left(t\right)$ 表示在c交叉路口西入口在t时刻车辆的到达率。

第n周期，b交叉路口对c交叉路口的协调相位红灯和黄灯期间的车辆的时间延误 ${\beta }_m$ 由两部分组成：第n-1周期消散剩余的车辆等待红灯的时间延误，第n周期红灯和黄灯期间到达的车辆等待红灯的时间延误，则：

${\beta }_m=\left(1-{\alpha }_{cwz}\right)t_i{q}_{cwzs}^{n-1}+{\displaystyle {\int }_0^{\left(1-{\alpha }_{cwz}\right)t_i}{q}_{cwzh}^n\text{d}t}$, (10)

其中 ${\alpha }_{cwz}$ 为绿信比。

在第n周期，b交叉路口对c交叉路口协调相位绿灯开始，在停车线前等待的车流依次消散，后面到达的车辆需要依次等待前面排队的车辆消散完后才能通过交叉口。理论上可以知道第n周期绿灯结束时，若第n-1周期消散剩余的车辆和第n周期期间内到达的车辆，比b交叉口对c交叉口协调相位的第n周期绿灯期间的最大消散量小，所以第n周期的b交叉口对c交叉口的协调相位的消散量就是第n-1周期消散剩余的车辆和第n周期期间内到达的车流量，不然消散量即为第n周期b交叉口对c交叉口协调相位的最大消散量。

第n周期b交叉路口对c交叉路口协调相位绿灯期间的消散量可表示为：

$q_{cwzx}^n=\min \{v_z{\alpha }_{cwz}{t}_i,q_{cwzs}^{n-1}+{\displaystyle \int t_i{q}_{cwz}\left(t\right)\text{d}t}\}$ (11)

其中x表示绿灯期间， $v_z$ 则表示绿灯期间直行车流的车辆消散速度。为了保证车辆和行人能够安全通过路口，各相位对于绿灯的时间要加以控制，并给出各相位绿信比的约束条件为：

$\frac{t_{\min }}{t_i}\le {\alpha }_{cwz}\le \frac{t_{\max }}{t_i}$ (12)

$t_{\min }$ 表示该路段车辆和行人安全通过交叉路口的最少时间， $t_{\max }$ 表示该路段车辆和行人安全通过交叉路口的最多时间。

综合以上分析，可以得到在第n周期，b交叉路口对c交叉路口的协调相位绿灯结束时，见表5，直行车道的消散剩余车辆数量为：

$q_{cwzs}^n=\max \{0,q_{cwz}^n-q_{cwzx}^n\}$ (13)

因此，第n周期的b交叉口对c交叉口的协调相位绿灯期间的车辆时间延误由两部分组成：车辆消散等待延误和消散剩余车流量的延误组成，由此得到绿灯期间的车辆时间延误为：

${\beta }_x={\displaystyle {\int }_0^{{\alpha }_{cwz}{t}_i}{q}_{cwzx}^n\text{d}t}+{\alpha }_{cwz}{t}_i{q}_{cwzg}^n$ (14)

综合以上红灯和黄灯期间的车辆时间延误和绿灯期间的车辆时间延误，得到总的第n周期b交叉口对c交叉口协调相位的车辆时间延误为：

$\beta ={\beta }_m+{\beta }_x$ (15)

即：

$\beta =\left(1-{\alpha }_{cwz}\right)t_i{q}_{cwzs}^{n-1}+{\displaystyle {\int }_0^{\left(1-{\alpha }_{cwz}\right)t_i}{q}_{cwzh}^n\text{d}t}+{\displaystyle {\int }_0^{{\alpha }_{cwz}{t}_i}{q}_{cwzx}^n\text{d}t}+{\alpha }_{cwz}{t}_i{q}_{cwzg}^n$

因此可以得到研究小区开放对周边道路的车辆时间延误影响。

Table 5. Proportion of straight traffic flow at intersection

表5. 交叉口直行车流的比例

2) 建立双目标优化模型

通过调整信号交叉口控制系统的周期时长和绿信比，可以使得信号交叉路口各入口方向的消散量最大；通过调整相邻信号交叉路口控制系统协调相位的相位差，可以使得相邻信号交叉路口间协调相位车辆时间延误最小。建立相邻交叉路口的双目标优化模型，可以增大消散量和减小车辆时间延误，因此，作建立模型前假设为，开放式小区周边道路建立红绿灯丁字路口b，与c交叉路口进行动态相位控制，可以尽可能的增大消散量和减小车辆时间延误，由此得出开放式小区对周边影响较大，且为正向影响。

优化模型 [9] 如下：

$\max Q_i={\displaystyle \underset{\phi \in \varnothing }{\sum }{\displaystyle \underset{\theta \in \omega }{\sum }{Q}_{i\phi \theta }^n}}$

$\min \beta ={\beta }_m+{\beta }_x$

$\text{s}\text{.t}\text{.}\{\begin{array}{l}{T}_{\min }\le T_i\le T_{\max }\\ {\displaystyle \underset{\phi \in \varnothing }{\sum }{\displaystyle \underset{\theta \in \omega }{\sum }{\alpha }_{i\phi \theta }}}\le 1\\ \frac{T_{\min }}{T_i}\le {\alpha }_{i\phi \theta }\le \frac{T_{\max }}{T_i}\\ {\alpha }_{i\phi \theta }>0\\ T_i>0\end{array}$

3) 分层序列求解模型

该优化模型共有两个指标：一是让消散量尽可能大、二是让车辆时间延误尽可能小，同时满足两个目标。若不分主要和次要将会导致计算结果的不精确。因此对于优化模型的求解需将其分主次。

a) 如何确定主要和次要目标

i) 站在人民的角度：人们出行的目的主要有上班、上学、购物、去医院、去各个单位办事等，无论以什么作为出行目的，人们想要到达目的地的心理都是迫切的，因此，以人民生活的幸福指数为主要考虑因素，能最大程度减小在路程上消耗时间，则应该以车辆时间延误为主要目标。

ii) 站在用人单位的角度：每个上司都希望自己的职员能够按时到达公司，并且希望中途外出办事时，可以以较高的效率、较快的速度完成任务，减小时间延误可以提高公司整体的办事效率，因此需要以车辆时间延误为主要目标。

iii) 站在社会的角度：为了加快社会高速发展，提升社会整体运作效率，在当今社会，开始以效率作为城市发展的代名词，减小车辆时间延误可以加快社会发展步伐，促进社会发展，因此以车辆时间延误为主要考虑目标为最佳。

b) 以车辆时间延误最小为主要目标，求解优化模型

$\min \beta ={\beta }_m+{\beta }_x$

$\{\begin{array}{l}{T}_{\min }\le T_i\le T_{\max }\\ {\displaystyle \underset{\phi \in \varnothing }{\sum }{\displaystyle \underset{\theta \in \omega }{\sum }{\alpha }_{i\phi \theta }}}\le 1\\ \frac{t_{\min }}{T_i}\le {\alpha }_{i\phi \theta }\le \frac{t_{\max }}{T_i}\\ {\alpha }_{i\phi \theta },T_i>0\end{array}$

c) 以消散量最大为次要目标，求解优化模型

通过上一次求解，得到最优 ${\beta }^{*}$ 值，接下来计算消散量，同时兼顾车辆时间延误最小，为确保方程一定有解，加入松弛变量 $\mu$，则优化方程为：

$\max Q_i={\displaystyle \underset{\phi \in \varnothing }{\sum }{\displaystyle \underset{\theta \in \omega }{\sum }{\alpha }_{i\phi \theta }}}$

$\{\begin{array}{l}{T}_{\min }\le T_i\le T_{\max }\\ {\displaystyle \underset{\phi \in \varnothing }{\sum }{\displaystyle \underset{\theta \in \omega }{\sum }{\alpha }_{i\phi \theta }}}\le 1\\ \frac{t_{\min }}{T_i}\le {\alpha }_{i\phi \theta }\le \frac{t_{\max }}{T_i}\\ \beta \le {\beta }^{*}+\mu \\ {\alpha }_{i\phi \theta },T_i>0\end{array}$

由Lingo软件计算可得：最优周期时长、相位绿信比、总消散量、协调相位的车辆时间延误，其结果见表6：周期时长[100, 180] (单位：s)相位差：0.27 s。

Table 6. Index calculation results before and after the opening of each community

表6. 各小区开放前后指标计算结果

由计算结果可得，小型小区总消散量提高了 $\frac{532-540}{540}\times 100\%=-1.48\%$

车辆延误减少了： $\frac{38.2-43.2}{38.2}\times 100\%=-13\%$

中型小区总消散量提高了： $\frac{1728-1324}{1324}\times 100\%=30.51\%$

车辆延误减少了： $\frac{42.8-32.3}{42.8}\times 100\%=24.5\%$

大型小区总消散量提高了： $\frac{2052-1580}{1580}\times 100\%=29.87\%$

车辆延误减少了： $\frac{52.5-39.6}{52.5}\times 100\%=24.57\%$

由上述计算结果可知，小型小区开放与否对周边道路没有好的影响，而中型小区和大型小区开放，对周边道路有极大的正影响。

4.2.2. 建立实际通行能力计算模型

根据文献 [8]，规定该路段基本通行能力 $C_0=2500\text{pcu}/\text{h}$，结合城市主干行车道宽度、方向分布等因素,建立实际通行能力计算模型：

$\rho =C_0\cdot f_1\cdot f_2\cdot f_3\cdot f_4$

式中各系数分别表示，

1) $f_1$ 表示行车道宽度对通行能力的修正系数，令其总宽度为9.75 m，则 $f_1$ 取值为1.0。

2) $f_2$ 表示方向分布对通行能力的修正系数，为50/50，则 $f_2$ 取值为1.0。

3) $f_3$ 表示路测干扰对通行能力的修正系数，城市主干道路干扰等级为2，则 $f_3$ 取值为0.83。

4) $f_4$ 表示城市道路组成对通行能力的修正系数，为关于i车型的交通量占总交通量的百分比( $P_i$ )、i车型的车辆折算系数的函数( E i )

$f_4=\frac{1}{1+{\displaystyle {\sum }_{i=1}^n{P}_i\left(E_i-1\right)}}$

车型分为：小轿车、公交车(单位通勤车、长途客车)、非机动车(摩托车、电动车、自行车) ( $i=1,2,3$ )，参数见表7。

Table 7. Parameter data applicable to the short circuit

表7. 适用于该短路的参数数据

由Matlab编程计算得到：

封闭式的实际通行能力：1.966825e + 03 pcu/h

开始式的实际通行能力：1.991363e + 03 pcu/h

实际通行能力提高百分比： $\frac{1.991363\times {10}^3-1.966825\times {10}^3}{1.966825\times {10}^3}\times 100\%=1.24\%$

实际通行能力每小时提高的车辆数： $1.991363\text{e}+03-1.966825\text{e}+03=24.53824辆车$

以上结果表明，开发式小区的实际通行能力比封闭式小区的实际通行能力提高了1.24%，平均每小时多通行24辆车。

4.3. 定量对比各类型小区开放前后对道路交通的影响

4.3.1. 建立Greenshields速度-密度关系模型

通过对车辆时间延误进行研究分析，结合通行能力来综合说明开放式小区对周边道路的影响。因此，需要建立Greenshields速度–密度关系模型，统计小区开放前后进入该路段的车流密度，计算车辆行驶的平均速度u：

$u=u_f\left(1-\frac{k}{k_{\max }}\right)$

式中， $k_{\max }$ 为路段的阻塞密度，取为135 veh/km， $u_f$ 为路段的自由流速度。

该路段为900 ± 150 m，

当该小区为小型小区时，取开放前的路段为400米，开放后的路段为180 + 20 + 200 (其中20米为b交叉路口路段长度)，

当该小区为中型小区时，取开放前的路段为800米，开放后的路段为370 + 30 + 400米(其中30米为b交叉口路段长度)，

当该小区为大型小区时，取开放前的路段为1000米，开放后的路段为450 + 50 + 500米(其中50米为b交叉路口路段长度)。

由该表8的计算结果可以看出，小区开放产生的效果与小区结构、周边道路结构及车流量有关。小型小区是否开放，对周边道路影响不大。中型小区和大型小区是否开放，对周边道路有显著性影响，因此除去考虑安全性因素，对于中型小区和大型小区可以开放。

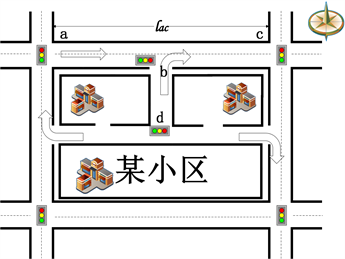
以上已经研究小区开放前后的车辆时间延误与实际通行能力，表明小区开放确实可以提高车辆的通行能力，且能减小车辆时间延误。接下来将研究不同类型的开放式小区，开放前后对道路通行的影响。图3(A)与图3(B)分别为本次设计的两种不同的开放式小区，小区开放产生的效果与小区结构及周边道路结构、车流量有关，接下来将应用以上建立的模型，定量比较开放式三岔口、四岔口小区。在开放前后，对道路通行的影响。

Table 8. Static properties of road segments

表8. 路段的静态属性

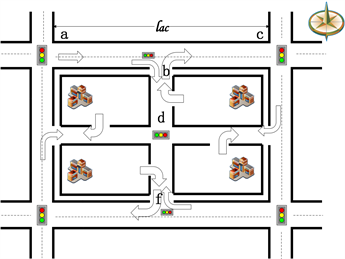(A) (B)

Figure 3. (A) Open three forks; (B) Open four forks

图3. (A) 开放式三岔口；(B) 开放式四岔口

4.3.2. 开放式三岔口

在相邻信号交叉路口控制系统的动态优化模型中，计算车辆时间延误时，需要考虑从各个方向进入主研究道路的车流量，与第二问中的开放式小区周边的车流量不同，需要考虑从d信号灯到来的车流量。因此将模型中的(8)式修改为：

$q_{cwz}^n=q_{cwzs}^{n-1}+P_{bwz}{q}_{bwz}^n+P_{bsy}\left(q_{bsys}^{n-1}+q_{bszs}^{n-1}+P_{dwz}{q}_{dwz}^n+P_{dey}{q}_{dey}^n\right)$ (16)

将上式(16)代入(15)中，得到开放式三岔口的车辆时间延误，而开放式三岔口的实际通行能力见表9：

Table 9. Index calculation results of different models of open Sanchakou

表9. 开放式三岔口不同车型的指标计算结果

由Matlab程序计算得：

封闭式的实际通行能力：1.966825e + 03 pcu/h

开放式三岔口的实际通行能力为：1.996152e + 03 pcu/h

实际通行能力提高百分比： $\frac{1.996152\times {10}^3-1.966825\times {10}^3}{1.966825\times {10}^3}\times 100\%=1.49\%$

实际通行能力每小时提高的车辆数： $1.996152\text{e}+03-1.966825\text{e}+03=29.32729辆车$

时间延误：封闭式42.8s，开放式30.5s，减少了28.73%。

以上结果表明，开发式小区的实际通行能力比封闭式小区的实际通行能力提高了1.49%，平均每小时多通行29辆车，时间延误减少了28.73%。

4.3.3. 开放式四岔口

在相邻信号交叉路口控制系统的动态优化模型中，计算车辆时间延误时，需要考虑从各个方向进入主研究道路的车流量，与第二问中的开放式小区周边的车流量不同，需要考虑从d交叉路口和f交叉路口到来的车流量，因此，将模型中的(8)式修改为：

$q_{cwz}^n=q_{cwzs}^{n-1}+P_{bwz}{q}_{bwz}^n+P_{bsy}\left(P_{dsz}{q}_{dsls}^{n-1}+P_{fwz}{q}_{fwz}^n+P_{fey}{q}_{fey}^n+P_{dwz}{q}_{dwz}^n+P_{dey}{q}_{dwz}^n\right)+q_{bszs}^{n-1}$ (17)

将上式(17)代入(15)中，计算得到的将是开放式四岔口的车辆时间延误。而开放式四岔口的实际通行能力见表10：

Table 10. The calculation results of the different models of the open four forks

表10. 开放式四岔口不同车型的指标计算结果

由Matlab程序计算得：

封闭式的实际通行能力：1.966825e + 03 pcu/h

开放式四岔口的实际通行能力为：2.011634e + 03 pcu/h

实际通行能力提高百分比： $\frac{2.011634\times {10}^3-1.966825\times {10}^3}{1.966825\times {10}^3}\times 100\%=2.27\%$

实际通行能力每小时提高的车辆数： $2.011634\text{e}+03-1.966825\text{e}+03=44.80944辆车$

时间延误：封闭式42.8 s，开放式43.1 s，增加了0.7%。

由上结果可知，开发式小区的实际通行能力比封闭式小区的实际通行能力提高了2.27%，平均每小时多通行44辆车，时间延误增加了0.7%。

通过以上定量分析比较各类型的开放式小区，发现当小区只开辟出一条支路时，比封闭式小区对周边道路影响要好。其主要原因在于减小了车辆时间延误、增大了实际车辆通行能力。当对三岔口和四岔口开放式小区进行研究计算，可得中型和大型小区进行开放，中型小区至多可开辟三岔口，大型小区开辟出的支路越多，车辆延误越小，车辆实际通行能力越好。

4.4. 合理化建议

1) 根据Greenshields速度–密度关系模型得到的结果，小型小区(90 × 90平方米)不需要进行开放设计，可以让小型小区继续保持封闭式原状，而中型和大型小区可以进行开放式设计；

2) 根据建立相邻信号交叉路口控制系统的动态优化模型的结果，在相邻两信号交叉路口中间，经过动态优化协调，可达到双目标，即增大交叉口消散量、减小车辆时间延误，同时，研究结果表明，两信号相位协调中间路长越短，增大消散量和减小车辆时间延误的效果越好，车辆的通行能力越好。因此，在对小区实行开放设计时，注意在丁字路口处，加设信号灯，并采用动态优化控制模型，进行优化协调相位控制，可以有效得增大消散量和减小车辆时间延误。

3) 根据各种类型开放式小区综合对比模型的结果，可以得到，中型小区至多开放三岔口，大型小区进行开放设计时，岔口越多，即开放支路越多，通行能力越好，开放后产生的效果越好。

5. 模型的验证与改进

5.1. 模型的验证

在谷歌地图上(图4)，随意选取一个B类城市的中型小区，调查其各类数据，验证模型的实际效用。

该小区的配时参数为：

信号灯周期为100s，绿信比为0.27，

时间延误为：31.8s

该小区上方路段小轿车占比为74.1%，公交车占比为8.7%，非机动车占比为17.2%，

实际通行能力为：1.988500e + 03 pcu/h

Figure 4. Cell location map

图4. 小区位置图

该计算结果与理论值相符，因此，以上所建模型正确。

5.2. 模型的改进

以上模型的求解均利用计算机编程计算，Lingo、SPSS、Matlab编程难度较大，费时较长，且有一定的误差。可引进Matlab仿真模拟的方法，简化模型的求解，提高模型计算结果的准确率。

具体可以这样操作，将该优化模型进行仿真模拟，令仿真时间为20 min，初始相位差假定为路段长度和其平均速度的比值，周期时长设置为150 s，相位绿信比设置为0.27和0.19，相邻交叉口协调相位的相位差为75 s，再以这些配时参数进行仿真模拟。

6. 结语

通过分析小区开放对周边道路的车流量、信号灯周期时长、相位差、绿信比及红、黄、绿灯期间的消散量的影响，建立相邻信号交叉路口控制系统的动态优化模型。以时间延误为主要目标，总消散量为次要目标，基于分层序列法求解该模型，经Lingo求解，得出小型小区的时间延误减少了−13%，中型小区减少了24.5%，大型小区减少了24.57%，结果表明，小型小区开放后对周边道路通行有反向作用，而中型和大型小区开放后对周边道路通行有正向作用。

以B类城市的中型小区作为研究对象，结合城市主干道路宽度、方向分布、路测干扰等因素，建立实际通行能力计算模型，经Matlab求解，得到二岔口开放式小区比封闭式小区的通行能力提高了1.24%，平均每小时多通行24辆车。

建立Greenshields速度–密度关系模型，得到不同路段和不同结构的小区，在开放前后的自由流速度，得知小区开放产生的效果与小区结构、周边道路结构及车流量有关。用Visio绘制三岔口、四岔口两种开放式小区，应用问题2)中的模型，改进模型中关于车流量的计算公式，对于各类型小区，定量比较其开放前后的时间延误和通行能力。经Matlab求解得到，三岔口小区时间延误减少了28.73%，通行能力提高了1.49%，平均每小时多通行29辆车；四岔口小区时间延误增加了0.7%，通行能力提高了2.27%，平均每小时多通行44辆车。

通过分析前三个模型求解到的结果，向有关部门提三点建议：可开放中型和大型小区；对B类城市的中型小区至多可按照三岔口类型开放三条支路，对大型小区可开放更多支路；在小区开放后形成的丁字交叉口和十字交叉口处，加设信号灯，且相邻交叉口进行动态协调相位控制，从而达到优化路网结构，提高道路通行能力，改善交通状况的目的。