1. 引言
摆动状态下的水翼广泛应用于直翼推进器、波浪能捕获和仿生推进等领域。在实验分析方面,Anderson等人使用粒子成像系统,对较低雷诺数流场状态下运动水翼的推力系数进行了实验研究,同时分析了不同攻角下的尾涡特性 [1]。在摆动翼型水动力特性影响因素分析方面,Young等人采用数值方法研究了呈正弦运动的水翼的尾流特性,发现尾涡结构以及翼型受到的升力和推力显著依赖于斯特劳哈尔数 [2]。Ashraf等人通过仿真模拟了对称翼型和非对称翼型的推力和推进效率,发现翼型厚度在特定雷诺数流动中对推力影响较大 [3]。Xiao等人通过仿真分析了有效攻角在翼型摆动过程中的作用以及其对推力大小和推进性能的影响 [4]。刘志恒发展了二维水翼定常绕流计算模型,并设计了扑翼装置进行试验验证 [5]。刘焕兴等 [6] 采用RANS求解器通过数值模拟分析了非正弦摆动下水翼的水动力性能,并探究了常规摆动情况下水翼性能较低的原因。马鹏磊 [7] 对流体诱导的振荡水翼进行了三维数值仿真模拟,分析了附加质量和附加质量矩对水翼水动力性能的影响。胡健等 [8] 采用重叠网格结合交界面数据传递的方法实现了摆动水翼的模拟,计算了水翼在不同斯特劳哈尔数下摆动所受到的作用力和力矩,并分析了尾涡产生的机理。张国政 [9] 计算了水翼在不同运动参数下的水动力性能,分析了水翼的推力以及功率特性,获取了水翼在不同工况下推进性能变化一般规律。郭春雨等 [10] 以采取不同前缘结构形式的三维水翼为对象进行了水动力模型试验,分析了水翼在不同摆动速度下的水动力性能。
上述研究中的摆动水翼主要将摆动轴设置在水翼中段,如最大厚度处或几何中心等,但缺少对翼型导边不动而尾缘摆动情况下的水动力分析,故本文针对该情况下不同摆动角度和来流速度的影响展开研究,为水翼的工程应用提供一定参考。
2. 几何模型
2.1. 水翼几何
本文分析的水翼模型采用NACA0012翼型,其中来流方向由前缘向后缘方向,几何模型如图1所示。
2.2. 计算工况
计算中,首先应用定常计算将某一速度工况下的流场计算稳定,然后应用非定常计算翼型以一定的旋转角速度进行摆动,摆动过程中保持翼型导边不动尾缘摆动,即水翼绕图1中左侧最前端摆动。具体的计算工况如表1所示。
翼型的摆动采用自定义函数,定义旋转速度为随着时间变化的分段函数。以工况摆动角度±5˚、±10˚、±20˚,摆动角速度100˚/s,计算时间为4个摆动周期。流体介质为水,其密度和动力粘度分别为997.561 kg/m3和0.00088 Pa×s。
3. 计算模型
3.1. 控制方程
流体分析过程主要遵循三大守恒定律,即:质量守恒定律、动量守恒定理和能量守恒定律。在数学方法上将三大定律表示为控制方程来实现。在一个单独的系统内,不论进行何种物理化学变化,其整体的质量不变。在流体中的表现就是在流入和流出的流体总质量保持不变。根据这一特性,得出流入控制体和流出控制体的流体质量相同,其守恒形式的方程如下:
(1)
其中ρ为流体密度,t为时间,V为流体速度。动量守恒是说明在系统不受外力或受外力合力为零的情况下,整个系统的总动量保持不变。该定律在流体中同样适用,在使用过程中的数学表达式为:
(2)
(3)
(4)
综合上式并表述为数值格式,采用RNG k-ε模型可得到控制方程如下
(5)
(6)
Gk是由层流速度梯度而产生的湍流动能,Gb是由浮力而产生的湍流动能,YM由于在可压缩湍流中,过渡的扩散产生的波动,C1,C2,C3,为常量,αk和αe是k方程和ε方程的湍流Prandtl数。
3.2. 计算网格
单翼型CFD水动力性能采用k-ɛ Realizable湍流模型,设置速度入口和压力出口层边界条件。计算翼型的摆动采用重叠网格,通过设置重叠域来实现翼型随时间的摆动。计算域的长度设置为1.8 m,其中速度入口距离前缘0.4 m,压力出口距离后缘为1.4 m,翼缘两侧距离边界为0.4 m。
分析中采用二维多面体网格,网格主要分为背景网格和重叠网格两部分,重叠网格位于背景网格之内,计算中背景网格在重叠网格的区域进行挖洞处理,重叠网格边界会背景网格进行插值计算,实现背景网格和重叠网格之间的流场信息交换,因此重叠网格对大幅运动的流场求解具有很大的优势,从而避免了物体大幅运动而产生的网格变形。
网格全局尺寸设置为0.01 m,翼型表面网格设置为0.002 m,并设置边界层数为5层,第一层边界层网格厚度为0.5 mm,对重叠网格区域进行两个阶梯性加密,其网格尺寸分别为2 mm和4 mm。网格如图2所示。
 (a)
(a)  (b)
(b)
Figure 2. Mesh: (a) Mesh of computational domain; (b) Mesh of boundary layer
图2. 计算网格:(a) 计算域网格;(b) 边界层网格
由图2(a)可以看到,背景网格中对重叠网格区域进行加密,其分为两个不同尺寸的加密区域,由重叠网格区域向外尺寸变大。
4. 计算结果与分析
计算不同工况下的翼型动态摆动流场分析,分析其速度、流场和升力阻力等流场信息。
4.1. 不同水翼摆角流场特性
分别计算来流为5 m/s、摆动角速度为100˚/s时摆动角度为±5˚、±10˚、±20˚的工况。
一个周期内±5˚摆角时4个典型位置的压力云图如图3所示,其中t = 0.05 s时刻为+5˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,最低压力为−14 kPa;t = 0.15 s时刻为−5˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,最低压力为−14 kPa;t = 0.1 s和t = 0.2 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生低压区域,根据各自的摆动情况,背面的低压区域大于迎面,其最低压力分别为−5.8 kPa和−5.9 kPa;不同时刻,其最大压力始终分布在翼型前缘。

Figure 3. Pressure contour of hydrofoil at 5˚ swing: (a) 0.05 s; (b) 0.1 s; (c) 0.15 s; (d) 0.2 s
图3. 水翼5度摆角下不同时刻压力云图:(a) 0.05 s;(b) 0.1 s;(c) 0.15 s;(d) 0.2 s
流场速度在t = 0.05 s时,其迎面(下侧)靠近前缘部位产生较大速度,最大速度为7.19 m/s;t = 0.15 s时,其迎面(上侧)靠近前缘部位产生较大速度,最大速度为7.10 m/s;t = 0.1 s和t = 0.2 s时刻,两侧均产生高流速区域;不同时刻,其最小流速始终分布在翼型前缘,且在后缘产生尾涡。
一个周期内±10˚摆动角的4个典型位置的压力云图如图4所示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,其迎面(下侧)靠近前缘处和背面(上侧)靠近后缘处产生较低压力,最低压力为−41 kPa;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)靠近前缘处和背面(下侧)靠近后缘处产生较低压力,最低压力为−42 kPa;t = 0.2 s和t = 0.4 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生低压区域,根据各自的摆动情况,背面的低压区域大于迎面,其最低压力分别为−6.8 kPa和−7.2 kPa;不同时刻,其最大压力始终分布在翼型前缘。
流场速度在t = 0.1 s时其迎面(下侧)靠近前缘部位产生较大速度,最大速度为9.83 m/s;t = 0.3 s时,其迎面(上侧)靠近前缘部位产生较大速度,最大速度为9.69 m/s;t = 0.2 s和t = 0.4 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域,不同时刻,其最小流速始终分布在翼型前缘,且在后缘产生尾涡。
一个周期内±20˚摆动角4个典型位置时的压力云图如图5所示,其中t = 0.2s时刻为+20˚摆动角,且向中间位置摆动,其迎面(下侧)靠近前缘处和背面(上侧)靠近后缘处产生较低压力,最低压力为−144 kPa;t = 0.6 s时刻为−20˚摆动角,且向中间位置摆动,其迎面(上侧)靠近前缘处和背面(下侧)靠近后缘处产生较低压力,最低压力为−149 kPa;t = 0.4 s和t = 0.8 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生低压区域,根据各自的摆动情况,背面的低压区域大于迎面,其最低压力分别为−6.2 kPa和−6.1 kPa;不同时刻,其最大压力始终分布在翼型前缘。
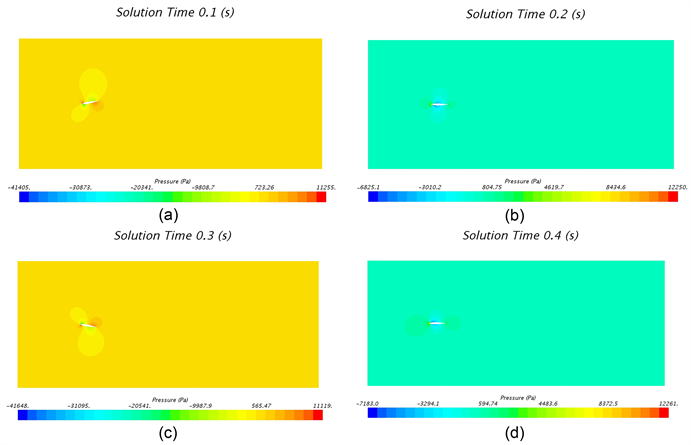
Figure 4. Pressure contour of hydrofoil at 10˚ swing: (a) 0.1 s; (b) 0.2 s; (c) 0.3 s; (d) 0.4 s
图4. 水翼10度摆角下不同时刻压力云图:(a) 0.1 s;(b) 0.2 s;(c) 0.3 s;(d) 0.4 s
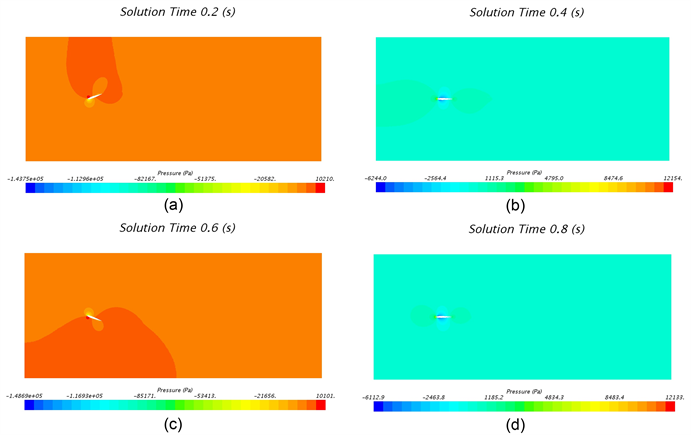
Figure 5. Pressure contour of hydrofoil at 20˚ swing: (a) 0.2 s; (b) 0.4 s; (c) 0.6 s; (d) 0.8 s
图5. 水翼20度摆角下不同时刻压力云图:(a) 0.2 s;(b) 0.4 s;(c) 0.6 s;(d) 0.8 s
流场速度在t = 0.2 s时,其迎面(下侧)靠近前缘部位产生较大速度,最大速度为15.81 m/s;t = 0.6 s时刻为−20˚摆动角,其迎面(上侧)靠近前缘部位产生较大速度,最大速度为16.05 m/s;t = 0.4 s和t = 0.8 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生高流速区域;不同时刻,其最小流速始终分布在翼型前缘,且在后缘产生尾涡。
可以看到不同摆动角度条件下,对称位置翼型所形成的流场也基本对称,最大流速均发生在摆动幅度最大,即攻角最大的位置,同时最大流速随着摆动角度的增大而增加。
4.2. 不同进流流场特性
分别计算摆动角度±10˚,摆动角速度为100˚/s时,来流速度为1 m/s、5 m/s和10 m/s三种状态下水翼尾缘摆动流动特性。
来流速度1 m/s时典型位置的压力云图如图6所示,其中t = 0.1 s时刻为+10˚摆动角,且向中间位置摆动,其迎面(下侧)处产生较高压力,背面(上侧)产生较低压力,最低压力为−6.8 kPa;t = 0.3 s时刻为−10˚摆动角,且向中间位置摆动,其迎面(上侧)产生较高压力,背面(下侧)处产生较低压力,最低压力为−7.2 kPa;t = 0.2 s和t = 0.4 s时刻,翼型位移摆动角为0˚的中间位置,两侧均产生低压区域,根据各自的摆动情况,背面的低压区域大于迎面,其最低压力分别为−369.49 Pa和−389.43 Pa;不同时刻,其最大压力始终分布在翼型前缘。
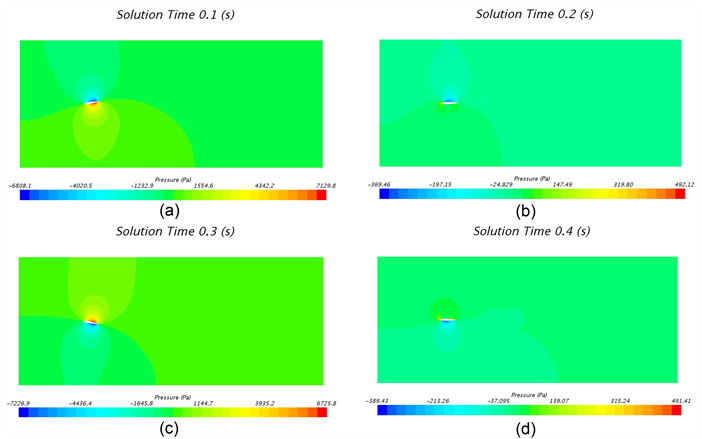
Figure 6. Pressure contour at 1 m/s inlet flow: (a) 0.1 s; (b) 0.2 s; (c) 0.3 s; (d) 0.4 s
图6. 来流1 m/s时不同时刻压力云图:(a) 0.1 s;(b) 0.2 s;(c) 0.3 s;(d) 0.4 s
来流速度10 m/s时典型位置的压力云图如图7所示,其中t = 0.1 s时,其迎面(下侧)靠近前缘处产生较低压力,最低压力为−185 kPa;t = 0.3 s时,其迎面(上侧)靠近前缘处产生较低压力,最低压力为−193 kPa;t = 0.2 s和t = 0.4 s时刻,两侧均产生低压区域,根据各自的摆动情况,背面的低压区域大于迎面,其最低压力分别为−27 kPa和−29 kPa;不同时刻,其最大压力始终分布在翼型前缘。

Figure 7. Pressure contour at 10 m/s inlet flow: (a) 0.1 s; (b) 0.2 s; (c) 0.3 s; (d) 0.4 s
图7. 来流10 m/s时不同时刻压力云图:(a) 0.1 s;(b) 0.2 s;(c) 0.3 s;(d) 0.4 s
不同流速下,以水平位置为参考,翼型在对称位置时刻所产生的流场基本呈现对称性,随着流速的提高,翼型所受到的压力也逐渐增大。
4.3. 水翼受力结果
根据计算结果提取不同摆动角度和速度下的最大升力和阻力曲线,如图8和图9所示。

Figure 8. Lift force and drag force of the hydrofoil at different swing angle: (a) Lift force; (b) Drag force
图8. 不同摆动角度下的升力和阻力:(a) 升力;(b) 阻力
由图8可以看到,在5˚~20˚范围内不同摆动角度情况下,随着摆动角度的增大,升力和阻力均增大,升力增加的速度逐渐减小,阻力增加的速度逐渐增大。随着摆角的增大,翼型在较大摆角时的迎风截面积明显大于在较小摆角位置时,因此阻力的增加可以认为是由于迎风面积增加所导致。
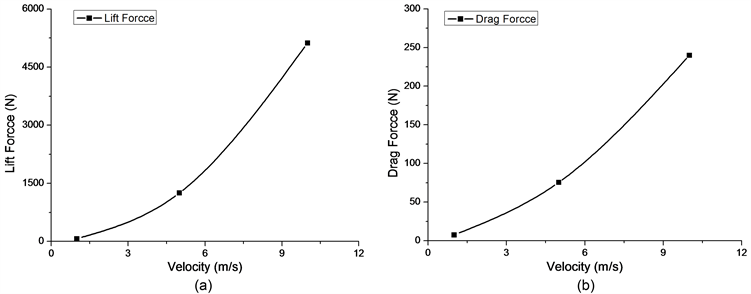
Figure 9. Lift force and drag force of the hydrofoil at different flow velocity: (a) Lift force; (b) Drag force
图9. 不同来流速度下的升力和阻力:(a) 升力;(b) 阻力
由图9可知,在1 m/s~10 m/s来流速度工况下,随着速度的增大,升力和阻力均增大,且升力和阻力增加的速度逐渐增大。水翼阻力的非线性增大与常见结构物绕流结论相似,即阻力与来流速度的平方相关,计算结果中由于摆动的影响阻力与流速的关系介于一次方和二次方之间。
5. 结论
通过对水翼不同摆动角度和来流速度下的流场进行计算,得到以下结论:
1) 在不同摆动角度工况下,压力分布和速度分布相互对应,流速较大的区域为低压区域,随着摆动角度的增大,最大压力变化较小,最低压力(负压)逐渐增大。
2) 在不同来流速度工况下,随着来流速度的增大,最大压力和最小压力(负压)均有不同程度的增大。
3) 通过对不同工况的升力和阻力曲线分析,随着摆动角度在5˚~20˚范围内增大,升力和阻力均增大,升力增加的速度逐渐减小,阻力增加的速度逐渐增大;随着来流速度在1~10 m/s范围增大,升力和阻力增大,且增加的速度逐渐增大。
基金项目
装备预研领域基金项目资助(No. 61402070503);武汉理工大学国家级大学生创新创业训练计划资助(No. 20191049702018);中央高校基本科研业务费专项资金资助(No. 2019IVA076)。
NOTES
*通讯作者。