相变蓄冷保温箱的模拟仿真与实验

Numerical Simulation and Experimental Investigation of Storage Box Using Phase Change Materials

摘要: 利用一种新型低温相变材料制作可以长时间维持低温的保温箱，测试新材料保冷性能并用模拟与实验对比探究低温材料的融化规律。利用自制保温箱做了空载实验，并利用ANSYS Fluent软件对空载箱内温度分布做出模拟。结果表明保温箱内上层蓄冷剂较快融化，底层维持低温时间较长，中间底面温度维持低温较久；底面模拟温度曲线与实验一致，中间温度差别大因为现实中存在自然对流热空气上浮，使得中间温度高于底面温度。利用ANSYS Fluent软件对箱内温度分布做出模拟，模拟温度曲线与实验一致，模拟得出蓄冷箱内部的融化一般是从边角开始，需要优化边角结构。因为有漏热存在，实验温度分层严重，而模拟因为条件理想化，不存在漏热，所以温度分布均匀，基本不存在分层。

Abstract: An insulated box was made from a new type of low temperature phase change material (PCM)., which is to test the thermal performance of this new type PCM and find the melting law of the PCM in this box . The no-load experiment was carried out with the self-made box. The results show that the proportion of the PCM in the upper layer can be increased because of the rapid melting of the PCM in the upper layer. The heat transfer model can ensure the cold storage time to meet people’s needs and also can be applied to the cold chain logistics system. ANSYS Fluent software was used to simulate the temperature variation of the box. The simulation results show that the bottom tem-perature curves are in agreement with the experimental results and consistent. There is a big dif-ference in the intermediate temperature because there is natural convection of hot air in the reali-ty rising so that the intermediate temperature is higher than the bottom temperature. The PCM’s melting inside the storage box usually starts from the corner and the corner structure needs to be optimized. Due to the presence of heat leakage, the experimental temperature is seriously strati-fied. However, in the simulation, the temperature distribution is uniform and there is basically no stratification because of idealized conditions and no heat leakage.

1. 引言

近年来，由于经济的发展和人民生活水平的提高，外出携带小型蓄冷装置，物流行业对于保温保鲜的要求都促进了蓄冷技术的发展。蓄冷是一项将低于环境温度的冷量储存起来以留后用的技术，它是制冷技术的补充和调整，是协调冷能在时间和强度上供需不匹配的一种经济可行的方法 [1] [2]。冷链物流要求食品从生产加工、储藏运输、销售到消费前的各环节始终处于食品所需的低温环境中，以保证食品质量的损耗降至最低。传统冷冻车在车辆行驶中制冷效果会受到发动机转速的影响，运输过程温度变化大，影响食品品质，并且存在噪声等问题 [3]。蓄冷型保温箱因其设备简单、成本低、温度控制精准、可以多品温货物共存 [4] 等优点正在受到越来越多研究者的关注。

国内外学者针对相变蓄冷材料在蓄冷保温箱中的实际应用进行了多方面研究。陈文朴 [5] 等以甲酸钠为主基材，制作出一种相变温度为−15.5℃，相变潜热为282 kJ/kg的无机相变蓄冷材料，并对两种蓄冷保温箱作了比较，得出真空绝热板–聚氨酯复合的蓄冷箱保冷效果明显优于聚氨酯蓄冷箱。许多研究表明在冷链中加入PCMs可以实现节能，Mashud Ahmed [6] 等用相变温度为7℃的石蜡基PCMs放在标准冷藏车壁上，发现单个壁面的峰值换热量降低在11.3%~43.8%之间，进入冷藏仓的总热流量减少了16.3%。Ming Liu [7] 等研制了一种相变温度为−26.7℃，相变潜热为154.4 J/g的新型相变材料，并制作一种新型蓄冷系统以维持普通卡车在合适温度，比普通系统大大节约了能源消耗。徐笑锋 [8] 等研发一种经济性较高，相变温度为6.4℃，相变潜热为141 J/g的硫酸钠水合盐体系，并比较了发泡聚丙烯保温箱和真空绝热板保温箱，发现真空绝热保温板的保温效果更佳。

而数值模拟的方法也是被广泛应用于保温箱的温度模拟。刘伟等 [9] 制作了一个外皮采用夹层硬质聚氨酯泡沫板的玻璃钢板的蓄冷式冷藏箱。利用COMSOL Multiphysics生成四面体网格并利用COMSOL对其进行模拟，得出模拟结果与实验结果吻合较好。田津津等 [10] 利用数值模拟的方法研究NaCl蓄冷板在不同初始温度下的释冷过程。赵慧妍等 [11] 探究了Fluent的里不同的模型下保温箱温度场的变化情况并与实验做出了对比。朱文娴等 [12] 利用COMSOL软件对食品冷藏保温箱的温度场做出模拟并做了实验的验证。此外还有很多国内外的学者利用软件模拟的方法来反应相变过程温度场，速度场以及压力场的变化 [2] [9] [13] [14] [15] [16] [17]。本文在前人研究的基础上，继续研究一种能维持足够长时间的低温环境的保温箱，采用一种以甲酸钠，氯化钾和水组成的新型有机无机相变蓄冷材料 [18]，并添加了二氧化钛作为成核剂降低过冷度，添加了黄原胶作为消除相分离的增稠剂。本文采用聚苯乙烯泡沫层和锡箔保温棉制作140 mm ´ 116 mm ´ 225 mm的自制保温箱，测量新型相变材料的保温性能，并利用fluent软件模拟简化模型的温度变化曲线。保温箱简约方便实用，可将其应用到平时家用外带冷藏食品。

2. 保温箱设计与实验

2.1. 保温箱的设计计算

蓄冷材料：配置出的相变蓄冷材料 [18] 是添加质量分数为0.6%纳米TiO₂和质量分数为0.6%黄原胶的凝胶型SPW (成分质量分数66%的蒸馏水、质量分数22% CHNaO₂和质量分数12% KCL)，相变温度为−24.6℃，过冷度为2.250℃，相变潜热为222.7 J/g，导热系数0.5437 w/m·k，比热容为3427 J/Kg·k。

保温箱：内为聚苯乙烯泡沫箱，外层包裹一层铝箔保温棉，具体数据与图像见表1，图1。

Table 1. Coefficient of insulation material

表1. 保温材料的系数

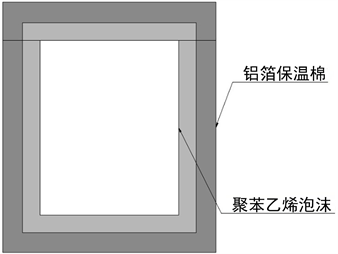
Figure 1. Section of box (vertical section)

图1. 保温箱截面图(竖直断面)

箱体的面积：

$S_o=2\ast \left(a_o\ast b_o+a_o\ast b_o+b_o\ast h_o\right)$ (1)

$S_i=2\ast \left(a_i\ast b_i+a_i\ast b_i+b_i\ast h_i\right)$ (2)

$S=\sqrt{S_o\ast S_i}$ (3)

式中 $S_o$ , $S_i$ , S分别为箱体的外表面积、外表面积和等效面积 [19] m²， $a_o$， $b_o$ 和 $h_o$ 分别为箱体外表面的长、宽和高，m。

计算得到传热面积为0.21 m²。

箱体内部与环境之间的传热计算：

箱体内部与外界环境之间的传热分为3个部分(忽略热辐射)：箱内空气与内表面的自然对流换热系数 $k_1$，箱体壁厚导热系数 $k_2$，箱体壁面与环境换热系数 $k_3$。为了简化模型，假设三部分传热过程对应的传热面积均为箱体的外表面积。箱体壁厚导热系数 [20]

$k_2=1/\left(\frac{{\delta }_1}{{\lambda }_1}+\frac{{\delta }_2}{{\lambda }_2}\right)$ (4)

${\delta }_1$ 、 ${\delta }_2$ 分别为泡沫层和保温棉的厚度 m， ${\lambda }_1$ 、 ${\lambda }_2$ 分别为泡沫层和保温棉层的导热系数， w/(m·k)。

箱内空气与壁面的传热过程和外壁面与环境之间的换热过程均可以简化成大空间自然对流，空气自然对流的传热系数的经验值范围(1~10 w/(m²·k) [10] )，由于外表面与环境温度接近，自然对流不强烈，故选取传热系数 $k_1=k_2=2$ w/(m²·k)。

总传热系数

$k_o=1/\left(\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}\right)$ (5)

根据公式算的传热系数为0.75 w/(m²·k) 。

传热温差：

$\Delta T=T_o-T_i$ (6)

$T_o$ , $T_i$ 分别为箱外环境温度和箱内冷藏温度，℃。

冷冻食品最佳冷藏温度为−18℃以下，所以选择最恶劣工况点，即箱内温度为−18℃ ，箱外为环境温度为23℃，所以温差为41℃。

总的散热量：

$Q=3600t{K}_{o}A\Delta T$ (7)

Q为散热量J； $K_o$ 为传热系数w/(m²·k) ；t为保冷时间h；A为传热面积m²； $\Delta T$ 为传热温差℃；

蓄冷剂的质量：

$m=\frac{Q}{H}$ (8)

m——蓄冷剂质量g；

H——相变蓄冷材料相变潜热J/g；本实验所用蓄冷剂的相变潜热为222.7 J/g。

2.2. 实验过程

2.2.1. 实验仪器

仪器：ZFXIMP-1C温度采集器，上海集研机电科技有限公司；DW-40低温试验箱，沧州鑫兴试验仪器有限公司；DF-101S磁力搅拌器，邦西仪器科技有限公司；BSM220.4分析天平，上海卓精电子科技有限公司；T型温度测量热电偶，美国OMEGA公司。

2.2.2. 实验步骤

根据公式7、8计算保冷8小时的相变蓄冷剂质量为0.836 kg，将配置好的不同质量的凝胶型复合相变蓄冷材料使用200 ml针筒分别平均装入6个自封袋中，而后置于−40低温试验箱冷冻备用。

首先做一个空载实验，将3个保温箱放于室温中，然后同时放入冷冻好的蓄冷袋，蓄冷袋放置于保温箱四周，根据潘欣艺等人 [13] 的研究，顶摆的方式对于箱内温度场的均匀程度来说是最佳的摆放位置，所以在每个保温箱内冰淇淋上放置上下左右共6袋，然后分别在三个保温箱底部、中部、上部、中边侧面以及环境各布置1个T型热电偶共四个热电偶，盖好保温箱箱盖，密封。将布置好的保温箱，放置室温进行放冷，对其进行温度记录，直到温度回升至室温为止，对比不同质量的蓄冷剂的保冷时间。

3. 模拟

3.1. 模型的建立

由8小时保温时长计算得到需836 g的蓄冷材料，需要690.9 ml的蓄冷材料，等效成等宽， $8x^3-1924x^2+147680x=690900$ (单位为mm)，使用牛顿法 $x_{k+1}=x_k-f\left(x_k\right)/f^{\prime }\left(x_k\right)$， $f^{\prime }\left(x_k\right)=24x_k^2-3848x_k+147680$ 求近似解得到宽度为4.99 mm。简化模型为等距的一层蓄冷剂，里面为空气，如图2所示。运用icem网格剖分功能对结构模型进行网格划分，利用其网格剖分工具和方法，生成结构型网格。如图3所示。本研究共涉及2个网格空间，145,920个节点，2个体空间，137,475个六面体网格，2个面，30,652个四边形网格空间，如图3所示。

Figure 2. The diagram of numerical model

图2. 模拟模型示意图

Figure 3. The diagram of grid

图3. 网格图

3.2. 数学模型及基本假设

由于物理模型自身的复杂性，在实际数值计算过程中，为了方便模拟仿真 [9] [21]，将模型简化为层流、非稳态、常物性、三维块模型，建立数值计算模型时做出如下假设：

箱体密封较好，不会发生严重漏气、漏冷；凝固融化过程是个随时间不断变化的过程，所以，在所有的微分方程中，不可忽略时间项的影响，所以该模型是个非稳态过程；空气为牛顿不可压缩流体，满足Boussinesq假设；不考虑辐射影响 [22]。

本研究使用Viscous模型研究冷藏过程中流场的分布，Viscous模型是一个适用于层流模型的计算模型，所以本文采用Viscous模型以及比较常用且成熟的SIMPLE算法对冷藏箱内保冷过程的温度场分布做出模拟，过渡过程使用PISO算法进行计算。考虑浮升力的影响，取重力加速度g = 9.81 m/s²。

采用有限体积法的控制方程，包括连续性方程、动量微分方程和能量微分方程，得到通用微分方程：

$\frac{\partial \left(\rho \varphi \right)}{\partial t}+div\left(\rho V\varphi \right)=div\left({\Gamma }_{\varphi }grad\varphi \right)+S_{\varphi }$ (9)

式中， $\varphi$ 为通用变量，可以代表 $u,v,w,T$ ； ${\Gamma }_{\varphi }$ 的广义扩散系数； $S_{\varphi }$ 的广义源项； $\rho$ 表示密度，kg/ m³； $V$ 表示速度的矢量形式，m/s。

3.3. 边界条件与求解

在自然对流中，可以用无量纲数–格拉晓夫数来衡量自然对流是层流还是湍流，如果 $1.43\times {10}^4<G_r<3\times {10}^9$，则属于层流；如果 $G_r>2\times {10}^{10}$，则属于湍流；如果 $3\times {10}^9\le G_r\le 2\times {10}^{10}$，自然对流属于层流与湍流的过渡阶段 [20]。

根据模型参数可以计算出保温箱内气流的格拉晓夫数。箱体的流体动力来自自然对流，根据箱体的尺寸条件通过格拉晓夫数求解公式，求得箱体的雷诺数 $G_r$ 低于10⁹，属于自然对流层流模型：

$G_r=\frac{g{\alpha }_v\Delta t{l}^2}{v^2}$ (10)

(10)式中， ${\alpha }_v$ 为体胀系数，本材料体胀系数为0.84 m³/kg；l表示长度特征尺度，本例为0.14 m； $\Delta t$ 温差，本例最大温差不超过20℃；g重力加速度，9.81 m/s²； $\nu$ 运动粘度系数，取15 * 10⁻⁶。

流体边界条件：由于无滑移边界条件，即所有固体表面上流体的速度等于固体表面的速度，所以： $u=v=w=0$。

热边界条件：边界为第二边界条件，影响贮藏箱热负荷的因素主要有：箱体传热的冷消耗、太阳辐射的冷消耗和箱体空气降温的冷消耗，由于箱体内空气储能很少可忽略不计，由于室内太阳辐射忽略，边界等热流密度为0.75 w/m²·k 。

模型求解：

箱体内流体设置为空气。结合试验数据，将箱内平均温度初始化为−30℃，空气以及蓄冷剂的温度初始化为−30℃，贮藏室内降温过程是一个瞬态过程，运用fluent瞬态求解器对箱体内部压力、速度和温度的耦合进行求解，添加重力影响因素，设置重力加速度为9.8 m/s²，设置时间步长为1 s，计算箱体的温度变化。

在数值计算过程中，通过液体体积率 [21] 来表示单位容积内液相组分的含量。液体体积率 $\beta$ [10] 定义为：

$\beta =\{\begin{array}{l}0,T<T_S\\ \frac{T-T_S}{T_L-T_S},T_S<T<T_L\\ 1,T>T_L\end{array}$ (11)

4. 结果与分析

4.1. 实验结果分析

由图4可以看出室温下进行不同质量的空载实验，外界温度为室温23℃左右，可以看出温度分层比较明显，上升趋势基本一致。可以看出箱子上层温度上升较快，也是相变平台最短暂的，而底部相变平台较为持久，这是因为冷空气的密度较大会下沉聚集在底部使得冷量沉积底部维持更长的相变平台。可以看出每部分的温度曲线在相变结束后先急剧上升之后再逐渐放缓。因为刚相变完的时候箱内外温差还比较大并且开始消耗显热之后由于箱内温度逐渐上升箱内外温差减小所以温升减缓再逐渐升至0℃以上。蓄冷箱内所有温度维持在相变温度都达到了5小时以上，中间储藏区的温度也达到了8小时的时长，能够满足人们外带食品保冷所需。

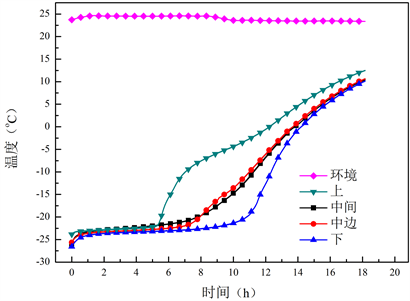
Figure 4. Temperature curve of no load experiment with 0.836 kg PCM

图4. 0.836 kg蓄冷剂空载实验温度曲线

4.2. 模拟结果分析

由图5可以看出，模拟与实验的下表面结果相差不大，开始时模拟温度上升的速度更大些，这是由

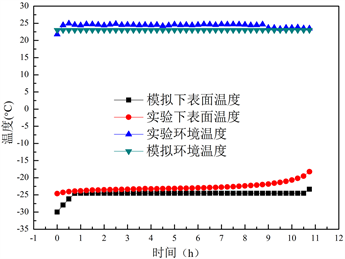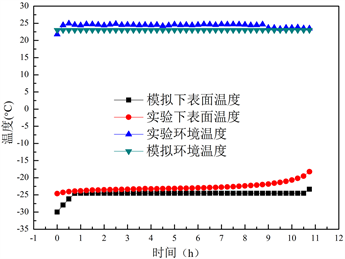(a) (b)

Figure 5. Experiment and simulation’s temperature contrast diagram

图5. 实验模拟温度对比图

于外界温度变化以及模型简化所致，模拟过程较为理想化，所以温度曲线较为规律。实验中由于不可忽略的影响因素导致相变过程较为快速，而模拟的相变温度则更加标准一些，这是由于漏热引起，由于箱内温度较低，压力也较低外界的热量会渗漏进来，导致实验的箱内温度较高，同时模型的简化也占一部分原因，由于现实中使用密封袋封装蓄冷剂，而模拟中是把蓄冷剂等效成均匀的一层。由箱内对比图可以看出，箱内温度上升的更快些，而模拟的箱内结果仍是和下表面一致，模拟的结果较为理想化，而现实中由于箱内自然对流使得箱内温度分层，箱中的温度明显上升的比下表面快。

如图6与温度曲线相对应，在相变过程中相变温度不变，液体体积率逐渐上升，等到液体体积率达到1时，意味着相变材料完全融化，相变材料开始释放显热，温度开始上升。由图7可以看出液体体积率的变化曲线与温度相对应，1小时达到相变温度开始融化，可以看出相变材料是从四周开始向中间融化，中间是空气液体体积率为1，周围是相变材料随着时间的变化液体体积率逐渐升高。10.68小时时周围相变材料和中间相变材料的液相体积率都达到了1已经完全融化。

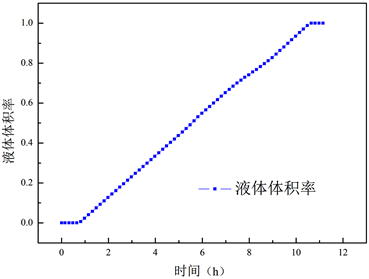
Figure 6. Simulation liquid fraction diagram

图6. 模拟液体体积率变化图

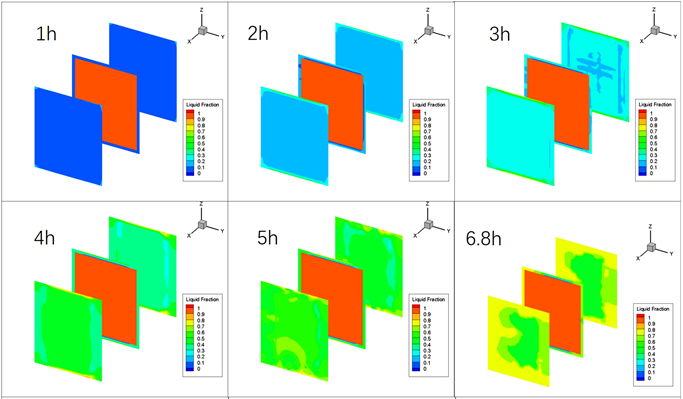
Figure 7. Actual change diagram of liquid fraction

图7. 液体体积率的实际变化图

从温度变化图8可以看出边角温度首先上升，中间温度上升较慢，大约1小时已经达到相变温度后一直维持在相变温度直到相变结束温度上升到249 K，相变过程持续了9.63个小时。从温度变化图可以看出相变材料层的温度小于等于其他地方的温度，对其他地方温度的维持起着主要作用。内部低温区呈现环形分布，将保冷物品放入环形区域保冷效果较好。

Figure 8. Temperature change diagram of simulation

图8. 温度变化图

5. 结语

1) 加装蓄冷材料会延长保冷时间，用传热模型计算所得的蓄冷剂质量将保温箱蓄冷时间维持在8小时左右，能够满足人们日常所需。

2) 经试验验证，保温箱底面保冷实验的温度模拟值与试验值随时间变化规律基本吻合，说明所建立的模型比较可靠。但有2℃左右的温差，这是因为实验环境温度不能完全稳定，实验一开始不能达到密封性要求，其次因为模型的简化，忽略掉了自封袋的不均匀性。

3) 通过对蓄冷式冷藏箱降温过程的数值模拟发现：相变材料从边角开始相变，分层可以优化边角。模拟与实验都验证蓄冷材料对保温箱的保冷具有主要的作用，可以将食品储存在保温箱环形区域内。采用fluent对蓄冷式冷藏箱降温过程中温度场的数值模拟具有一定的科学性，有助于认清温度场分布规律，为蓄冷式冷藏箱降温过程的参数优化提供参考。